画Bezier曲线：Casteljau算法

本文转载自德卡斯特里奥算法（De Casteljau’s Algorithm）绘制贝塞尔曲线 - 杨溪 - 博客园 (cnblogs.com)

 

德卡斯特里奥算法可以计算贝塞尔曲线上的点C(u)，u∈[0,1]。因此，通过给定一组u的值，便可以计算出贝塞尔曲线上的坐标序列，从而绘制出贝塞尔曲线。

德卡斯特里奥算法的基础就是在向量AB上选择一个点C，使得C分向量AB为u:1-u（也就是∣AC∣:∣AB∣= u）。给定点A、B的坐标以及u（u∈[0,1]）的值，点C的坐标便为：C = A + (B - A) * u = (1 - u) * A + B * u。

  

       定义贝塞尔曲线的控制点P_i编号为0i，其中，0表示是第0次迭代。当第一、二、三……次迭代时，0将会被1、2、3……替换。

       德卡斯特里奥算法的思想如下：为了计算n次贝塞尔曲线上的点C(u), u∈[0,1]，首先将控制点连接形成一条折线00-01-02……0(n - 1)-0n。利用上述方法，计算出折线中每条线段0j-0(j+1)上的一个点1j,使得点1j分该线段的比为u:1-u。然后在折线10-11-……-1(n-1)上递归调用该算法，以此类推。最终，求得最后一个点n0。德卡斯特里奥证明了，点n0一定是曲线上的点。

 

 

 

 

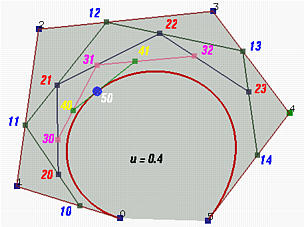
如上图，曲线控制点是00、01、02、03、04、05。线段00-01上取点10，10分该线段的比为u:1-u，类似地取点11、12、13、14，然后第二次迭代在线段10-11上取点20，点20分该线段的比为u:1-u，类似地取点21、22、23。然后进行下一次迭代，依次类推，直到最后在线段40-41上取点50，50是最终惟一的点，也是在曲线上的点。

上述直观的算法描述可以表达成一个计算方法。 

 

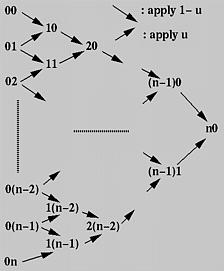
首先，将所有给定的控制点排列成一列，在上图中，即为最左边的一列。每一对相邻的控制点可以伸出两个箭头，分别指向右下方和右上方。在相邻箭头的交叉处，生成一个新的控制点。例如，控制点ij和i(j +1)生成新的控制点(i + 1)j。指向右下方的箭头表示乘以(1 - u)，指向右上方的箭头表示乘以u。

因此，通过第0列，可以求出第1列，然后求出第2列……，最终，在n次迭代后，可以到达惟一的一个点n0，这个点就是曲线上的点。

 

 

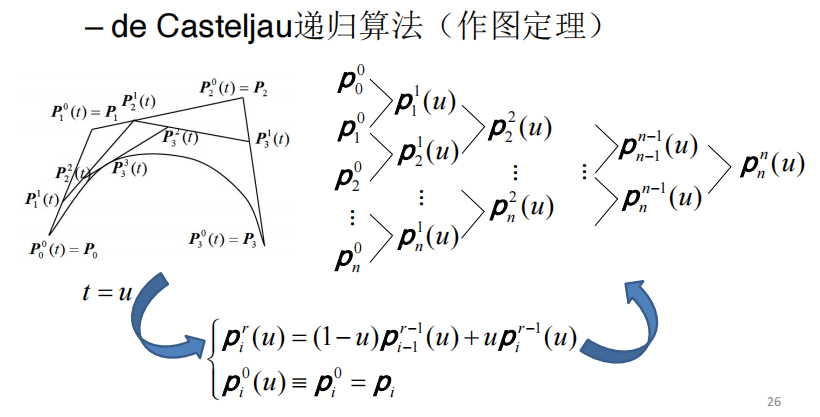
根据上述方法，我们可以根据给定的精度来确定一组u，根据u来计算贝塞尔曲线的一组坐标值。

void deCasteljau3D(pointArray& ctrlPts, int precision) {
    int n = ctrlPts.length;
    if (n < 2)return;
    float* xarray = new float[n - 1];
    float* yarray = new float[n - 1];
    float* zarray = new float[n - 1];
    float x = ctrlPts.arr[0].x;
    float y = ctrlPts.arr[0].y;
    float z = ctrlPts.arr[0].z;

    for (int k = 0; k <= precision; k++) {//根据计算出的坐标连线precision次
        float u = float(k) / float(precision);
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j < n - i; ++j) {
                if (i == 1) {//第一次迭代根据控制点得出
                    xarray[j] = ctrlPts.arr[j].x * (1 - u)
                        + ctrlPts.arr[j + 1].x * u;
                    yarray[j] = ctrlPts.arr[j].y * (1 - u)
                        + ctrlPts.arr[j + 1].y * u;
                    zarray[j] = ctrlPts.arr[j].z * (1 - u)
                        + ctrlPts.arr[j + 1].z * u;
                }
                else {//通过上一次迭代结果计算
                    xarray[j] = xarray[j] * (1 - u) + xarray[j + 1] * u;
                    yarray[j] = yarray[j] * (1 - u) + yarray[j + 1] * u;
                    zarray[j] = zarray[j] * (1 - u) + zarray[j + 1] * u;
                }
            }
        }
        glColor3f(0.0f, 1.0f, 1.0f);
        glBegin(GL_LINES);
        glVertex3f(x, y,z);
        glVertex3f(xarray[0], yarray[0],zarray[0]);
        glEnd();
        x = xarray[0];
        y = yarray[0];
        z = zarray[0];
    }
    delete[] xarray;
    delete[] yarray;
    delete[] zarray;
}