[学习笔记] Constraint Optimization
Constraint satisfaction problem (CSP) (约束满足问题)
Definition: "mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations" (Wikipedia)属于AI和Operation Research研究的领域.
可以建模为CSP的问题有: 四色问题, Sudoku等.
Formal definition
Formally, a constraint satisfaction problem is defined as a triple
, where X is a set of variables, D is a domain of values, and C is a set of constraints. Every constraint is in turn a pair 
, where t is a tuple of variables and R is a set of tuples of values; all these tuples having the same number of elements; as a result R is a relation. An evaluation of the variables is a function from variables to domains,
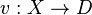. Such an evaluation satisfies a constraint 
if 
. A solution is an evaluation that satisfies all constraints.
Example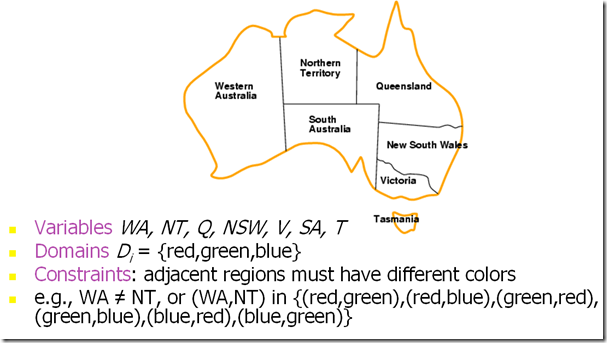 
求解CSP问题的方法
Constraint satisfaction problems on finite domains are typically solved using a form of search.
Backtracking
Constraint learning
Constraint propagation
Local search
Constraint optimization problem (COP) (约束优化问题)
定义
"defined as a regular constraint satisfaction problem in which constraints are weighted and the goal is to find a solution maximizing the weight of satisfied constraints." (Wikipedia)
定义一个objective function, 对于CSP的每一个解, 计算出objective function的值. 使objective function的值最优的就是COP的解.
(4C Outreach Programme)
IP与CP的比较
CP: a much richer constraint language
IP: more efficient algorithms to solve linear arithmetic constraints
Constraint programming (约束编程)
"a programming paradigm where relations between variables are stated in the form of constraints" (Wikipedia)
是一种declarative programming, 不像imperative programming需要指定执行的步骤.
Constraint programming最早源于constraint logic programming, 当前比较流行的CLP语言如Prolog.
部分imperative programming语言通过独立的包来支持constraint programming, 比如Choco (for Java), Comet( for C). etc.
另外Common Lisp也支持constraint programming.
有专门针对CP的国际会议: International Conference on Principles and Practice of Constraint Programming（一年一届, 今年第15届了)
References
* Wikipedia,
* CSP Tutorial, http://4c.ucc.ie/web/outreach/tutorial.html
* Michela Milano, Chapter 3, Branch-and-infer: a framework for combining CP and IP, Constraint and integer programming: toward a unified methodology, Google Books
