bilstm+ctf 吐血的理论讲解
Bilstm+crf 常用于序列标注任务，例如命名实体识别，词性标注
以 “人家是小萌新”作词性标注为例，分词后为“人家 是 小萌新”，对应的词性为名词，动词，名词
为简化问题，假设词性只有名词和动词两类，
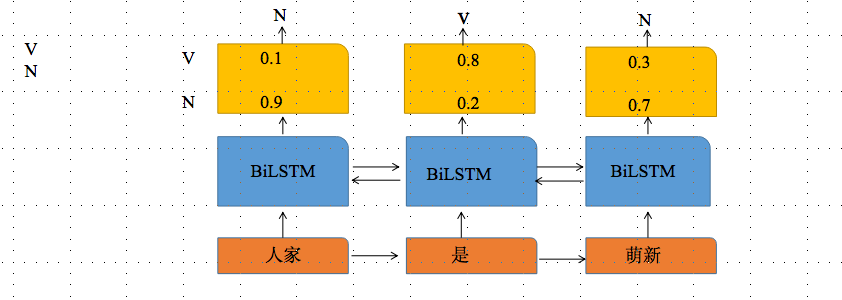
Bilstm 输出为每个词stoftmax输出最大概率值对应的label，只用BiLSTM的话，输出label之间是独立的但传统BiLSTM的不足未考虑到标签之间的相互约束性，比如假设Bilstm输出的最可能标签序列为"NVV",但根据标签转移矩阵，"V→V“概率很小，那么根据得分定义，这种序列不太能得到较高分数
-
为什么要有CRF层呢
CRF是判别模型，在词性标注栗子里，X对应的是单词序列，Y则是对应的单词词性
分词后为“人家 是 小萌新”，对应的词性为名词，动词，名词，为简化问题，假设词性只有名词和动词两类，对于三个词来说，共有2 3=8种路径，其中真正的路径是【N→ V→ N]
要做的就是 使得真实路径的得分在所有路径得分中最大，加上log 变成对数损失函数，再前面加上负号 就变成最小化损失函数，下图所示
如图总结到， 最终的损失函数等于 所有路径得分总和 - 真实路径得分
现在问题转化为 1、怎么定义一条路径的得分
2、怎么计算所有路径总分（肯定不会是暴力举出所有可能的路径啦，前向）
3、怎么预测隐变量-标签（维特比算法来解码）
下面一点一点展开来说；
1、一条路径得分定义为 转移特征函数 和状态特征函数的加和。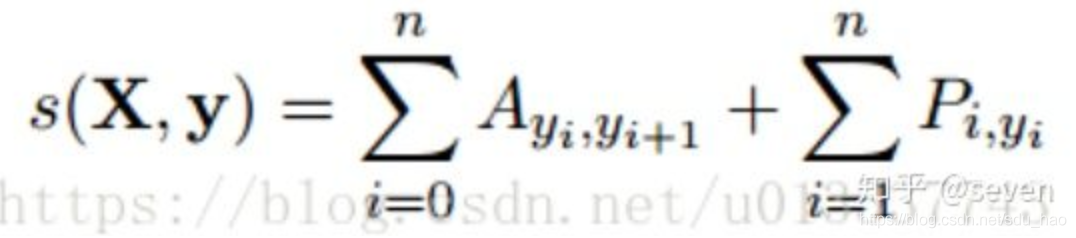
Pi,yi 表示的是 第i 个token 输出为yi词性)的概率，Ayi,yi+1 表示的是 前一个标签转 yi移到下一个标签 yi+1的概率。假设共有N个标签，则转移概率矩阵为(N+2) *(N+2)
以START→N→V→N→END 这条真实路径为例，EMISSION_SCORE=X0,START + X1,N + X2,V + X3,N + X4,END
TRANSITION_SCORE= TSTART→N + TN→V + TV→N + TN→V + TV→END , 这些分数来自于CRF层
整个过程中需要训练的参数为：
- BiLSTM中的参数
- 转移概率/得分矩阵A
2、计算所有路径总分
整个过程是一个分数的前向滚雪球的过程。它的实现思想有点像动态规划。首先，w0所有路径的总分先被计算出来，然后，我们计算w0 -> w1的所有路径的得分，最后计算w0 -> w1 -> w2的所有路径的得分，也就是我们需要的结果。状态分数定义如下
| N | V | |
| W0 | X0,N | X0,V |
| W1 |
X1,N | X1,V |
| W2 |
X2,N | X2,V |
转移矩阵如下
| N | V | |
| N | TN→N | TN→V |
| V | TV→N | TV→V |
设置两个变量，previous_score 表示 到上一个位置的路径总分，current_info 表示考虑当前位置的token 带来的新信息
对于第一个词W1,有两条路径START→ N ,START→V,得分分别为X1,N ，X1,V
对于第二个词来说，现在previous_score=（X1,N ，X1,V），cur_info=(X2,N ，X2,V）,transition_score=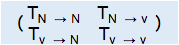
现在因为维度不同，三个矩阵不能相加，因而将previous_score，cur_info 扩展为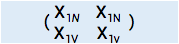 
, 
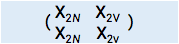,三个矩阵相加得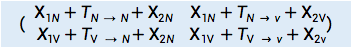
这个矩阵中的四个值分别对应的是从W1 到W2 的四条路径的得分。
第一次写博真的发现不是个轻松活，OK，继续迭代一次！
从W2→ W3,现在我们的previous_score 为上一步的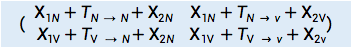，cur_info=(X3,N ，X3,V）,transition_score=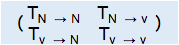
3、预测标签（词性）
在效率方面相对于粗暴地遍历所有路径，viterbi 维特比算法到达每一列的时候都会删除不符合最短路径要求的路径，大大降低时间复杂度。
w1→w2 ,假设W1最佳预测结果是N, 三矩阵相加后=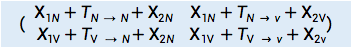
，对矩阵一列选列最大值（标红显示），W2被预测为N标签的最大得分为0.5（路径为N →N，W2被预测为V标签的概率为0.6(N→V)
我们有两个变量来储存历史信息，best_score 和 best_score_id,在每轮迭代中，我们将最佳分数存储到best_score，同时，最佳分数所对应的类别索引(N标签：0，V标签：1)存储到best_score_id
best_score=[[0.5,0.6]],best_score_id=[[]]
