97. 交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm
|n - m| <= 1
交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
提示：a + b 意味着字符串 a 和 b 连接。 

示例 1：

 

 

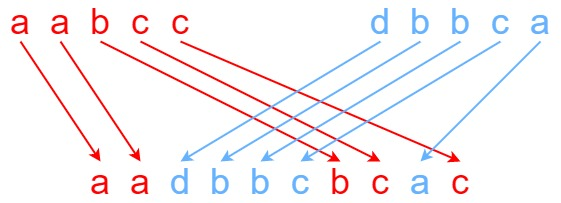
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true
示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false
示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true
 

提示：

0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和 s3 都由小写英文字母组成

解法: 动态规划

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        # 动态规划写法(双指针写法会少判断)
        if len(s1 + s2) != len(s3): return False

        # 初始化
        len1, len2, len3 = len(s1), len(s2), len(s3)
        dp = [[False for _ in range(len2 + 1)] for _ in range(len1 + 1)]
        dp[0][0] = True 

        # 边界
        for j in range(1, len2 + 1):
            dp[0][j] = dp[0][j - 1] and s2[j - 1] == s3[j - 1]
        
        for i in range(1, len1 + 1):
            dp[i][0] = dp[i - 1][0] and s1[i - 1] == s3[i - 1]
        
        # 状态转移方程
        for i in range(1, len1 + 1):
            for j in range(1, len2 + 1):
                # 依赖上一个 + 当前 == s3
                dp[i][j] = (dp[i][j - 1] and s2[j - 1] == s3[i + j - 1]) or (dp[i - 1][j] and s1[i - 1] == s3[i - 1 + j])
        
        return dp[-1][-1]