本质矩阵、基本矩阵、单应矩阵

对极约束
　　参考于：https://zhuanlan.zhihu.com/p/33458436

　　

 

 

 　　介绍
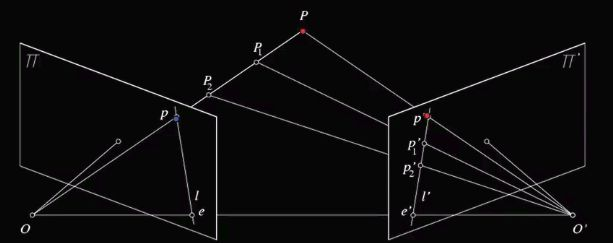
　　　　如果仅有一个视角，我们并不知道深度信息，如果有两个视角，我们就能得到深度信息
　　　　上图O,O' 是两个相机中心，P是物体再空间的位置，再左边的图像π中成像是p，在右边的图像π’的成像是p'
　　概念
　　　　基线：OO'
　　　　对极平面：OO'P
　　　　对极线：对极平面和两相机图像的交线l和l',
　　　　对极点：OO'和量图像的交点e，e'　　　

本质矩阵
　　什么是本质矩阵
　　　　本质矩阵，essential matrix。观测点P在相机1坐标系中的坐标可以通过缸体变换变成相机2坐标系下的坐标
　　　　本质矩阵就是 两个视角相机坐标系的转换

　　　　

　　 什么约束条件
　　　　

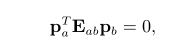
　　　　 其中Eab就是本质矩阵， 他的参数由
　　推到
　　　　

　　特点
　　　　描述空间中的一个点，在不同视角下的几何约束关系
　　　　本质矩阵和相机外参有关系，和内参无关系
基本矩阵
　　什么是基础矩阵？Fundamental matrix
　　　　基础矩阵，在不同视角下的图像的对应关系，是单应矩阵的一个特例
单应矩阵
　　参考于：
　　　　http://blog.itpub.net/31562045/viewspace-2220170/
　　什么是单应矩阵呢？Homography matrix
　　　　同一个平面的点，在不同图像之间的关系
　　　　这种关系不一定是同一物体，不同视角下的关系。比如我们举例的银行卡
　　　　但是  我们一般在介绍的时候，都是在说在不同视角下的图像的对应关系，这个时候和基本矩阵的关系是对应的
　　举例说明
　　　　银行卡拍摄的时候，可能会有倾斜，这个时候进行数字识别，准确率可能会低
　　　　经过单应矩阵变换后，将其摆正，然后就有比较高的准确率了。
　　　　不仅仅是倾斜的银行卡上面某一个点和摆正后的银行卡对应点上，满足单应矩阵的关系；
　　　　而是倾斜银行卡上面所有点和摆正后的银行卡上所有点都满足单应矩阵关系
　　　　这里就体现了同一个平面，不同图像之间的观点
　　世界坐标系-》图像坐标系
　　　　

 

 

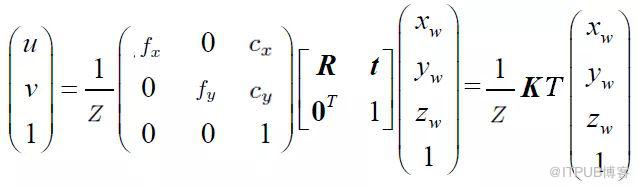
 　　简化一下，将中间的部分记做M
　　　　

 

 

 　　M是一个4*4的矩阵，如果空间点在同一平面上，那么我们可以将ZW=const（常数，设置可以为0），这样M就是一个3*3的矩阵了
　　两个不同的视角，像素坐标系和空间坐标系可以如下表示
　　　　

 

　　我们将上述两个式子合并成一个式子，找出一个平面，在两个视角图像坐标系成像之间的关系
　　H就是单应矩阵