相机模型 + 世界坐标系+相机坐标系+图像坐标系

针孔相机模型
　　　

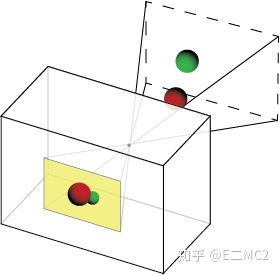
　　已知条件
　　　　假设有一个暗室（上图中的立方体），暗室的墙上有一个小孔（上图中的那个实心的点）；
　　　　暗室中有一个白板（上图中的那个黄色的矩形）；实际中的物体（红绿色小球）；
　　如何成像
　　　　小孔成像
　　成像特点：
　　　　镜像的，将3D信息压缩到了2D
　　等效模型
　　　　由于上面介绍的图像是镜像的，不利于数学分析。数学中会用到正负号
　　　　我们在小孔另一侧，和小孔相同距离位置的地方，放置另一个白板。这样就是等比例，无反向的了。
针孔相机的一些问题
　　无穷小的针孔的问题
　　　　我们上面假设的针孔是无穷小的，这样在理论分析中是可以的，但是实际中无穷小的针孔进入的光线是极其有限的。
　　　　因此我们可以扩大这个针孔来增加光量
　　扩大针孔造成的问题
　　　　扩大一个针孔，会使得成像平面上的影像模糊
　　模糊怎么办呢
　　　　一种方法是在针孔后面增加一个透镜，将通过较大针孔的光线聚焦。
　　　　实际中往往使用一组透镜，但是即便这样，也只能保证三维世界中一定距离的物体投射到成像平面清晰。
专有名词
　　焦距：小孔到成影平面的距离
　　投影中心、相机中心：就是我们说的针孔
　　景深：加上透镜后，相机能清晰成像的范围
相机坐标系

 　　

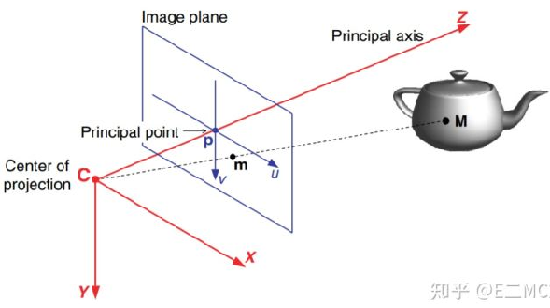
 　　相机坐标系 是三维的，他是右手坐标系，z轴是相机的主光轴。
　　空间中一点M投影到成像平面的位置是m，其中的投影关系满足相似关系
　　上面坐标系中包含一个像平面坐标系

图像坐标系

　　

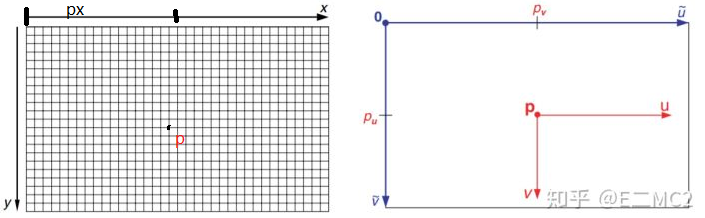
　　上图右边是像平面坐标系（以中心点为原点），箭头方向为正方向
　　左边的是图像坐标系（以左上角为原点），箭头方向为正方向
相机坐标系->像坐标系->图像坐标系的关系
　　相机坐标系下有一点
　　　　M（X，Y，Z）
　　像坐标系下坐标           
　　　　（u，v）
　　图像坐标系下坐标       
　　　　 (x, y)
　　相机坐标系--》像坐标系
　　　　

 　　像坐标系--》图像坐标系
　　　　

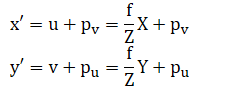
　　图像坐标系是以像素为单位的，上面还是以现实的距离为尺度的，来我们继续操作
　　　　
　　　　　

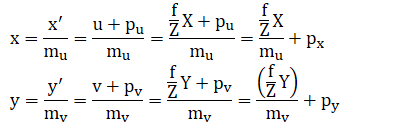
 　　　　整理一下
　　　　　　
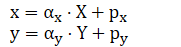
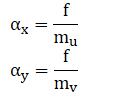　　　　　　表示焦距f在图像坐标系上 以像素为单位的 表示
相机-图像坐标系的矩阵表示-相机内参矩阵
　　

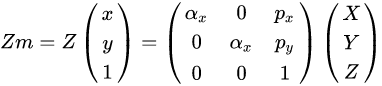
 　　等式最右边相当于图像坐标系乘以了Z深度。
　　这样一个3*3的矩阵就表示了 真实的相机坐标系下，一个点是怎么成像到图像坐标系的了
　　更常用的矩阵
　　　　

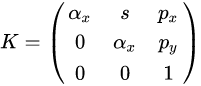
 　　　　参数s被称为skew，这个参数用来姜末像素是平行四边形而不是矩形的参数。
　　　　可以认为是传感器的安置不严格和相机主光轴垂直造成的变形的近似
　　当s=0的时候，像素为矩形。
　　　　

　　s！=0的时候，像素为平行四边形
　　　　

 世界坐标系和图像坐标系-相机外参
　　世界坐标系的引出
　　　　上面我们研究中，将相机坐标系看做了世界坐标系。但是，如果我们的系统中有16个相机呢？
　　　　那我们以哪个相机坐标系作为坐标系呢？并且相机坐标系和我们复合习惯的世界坐标系还不太一样？
　　世界坐标系和相机坐标系的图示

　　　　 

 　　　　看，我们的相机坐标系C和世界坐标系O并不重合。
　　　　我们定义一个旋转矩阵R,表示相机坐标系和真实坐标系之间的关联
　　　　我们用一个更清晰的图示吧
　　　　　　

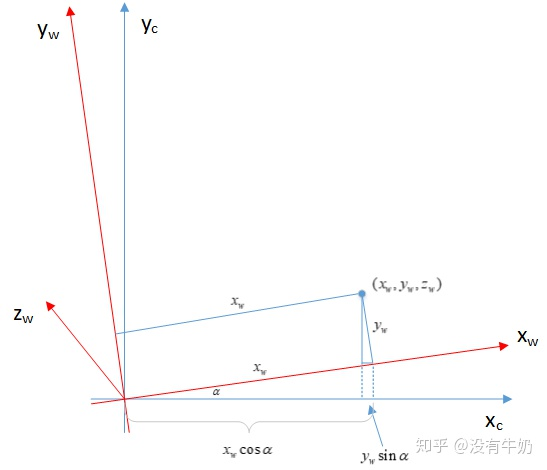
　　　　世界坐标系中的一个三维点M要转换到相机坐标系下
　　　　　　第一步：先旋转，保证两个坐标系的方向相同
　　　　　　　　
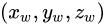
　　　　　　　　　　世界坐标系中的一点，
　　　　　　　　Xc=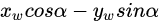
　　　　　　　　　　对应相机坐标系中的x坐标
　　　　　　　　Yc =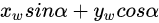 
　　　　　　　　　　对应相机坐标系中的y坐标
　　　　　　　　
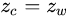
　　　　　　　　　　因为我们是沿着Z轴旋转的，因此，我们z的数值不变
　　　　　　　　写成矩阵
　　　　　　　　　　

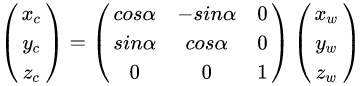
 　　　　　　　　上面3*3的矩阵就是r1
　　　　　　　　同样关于x轴，y轴的旋转矩阵是r2、r3
　　　　　　　　
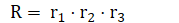
　　　　　　　　　　总的旋转矩阵
　　　　　　第二步：再平移
　　　　　　　　

 　　　　　　整体的矩阵描述

　　　　　　　　

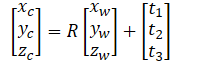
　　　　　　矩阵的增广形式
　　　　　　　　

 　

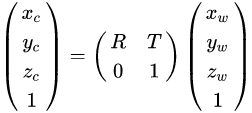
 整体关系
　　

 

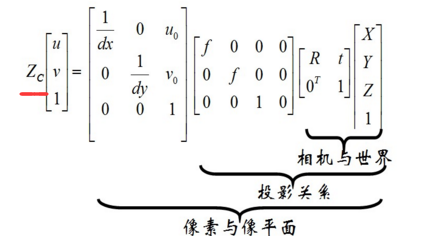
 　　前两个是投影矩阵，这个可以组合成一个
　　第三个是世界坐标系转换矩阵