贪心算法基础及leetcode例题

参考

理论

本质：找到每个阶段的局部最优，然后去推导得到全局最优
两个极端：常识&&很难：

很多同学通过了贪心的题目，但都不知道自己用了贪心算法，因为贪心有时候就是常识性的推导，所以会认为本应该就这么做！

套路：
贪心没有套路，说白了就是常识性推导加上举反例
做题的时候，只要想清楚 局部最优 是什么，如果推导出全局最优，其实就够了。

贪心算法一般分为如下四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解
这个四步其实过于理论化了，我们平时在做贪心类的题目 很难去按照这四步去思考，真是有点“鸡肋”。

Leetcode题目

简单题

455.分发饼干

思路：大饼干 喂 胃口大的kid，才能充分利用

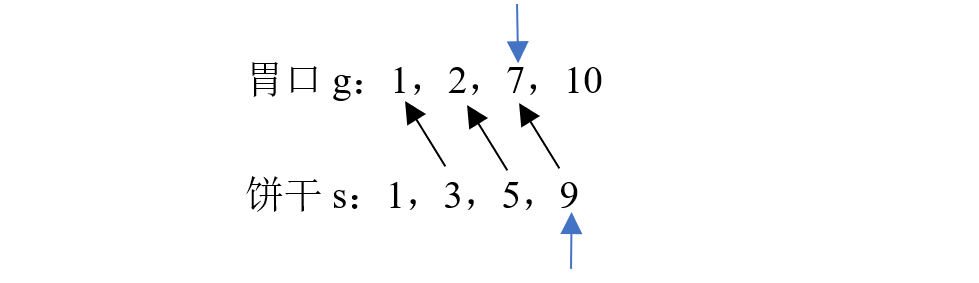
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int j=s.length-1;
        int sum = 0;

        for(int i=g.length-1;i>=0;i--){
            if(j>=0 && s[j]>=g[i]){
                sum++;
                j--;
            }
        }
        return sum;
    }
}

中等题

序列问题---376. 摆动序列

思路：考虑情况

记录摆动条件：
prediff>0 && curdiff<0
或者 prediff<0 && curdiff>0

情况1：上下坡中有平坡

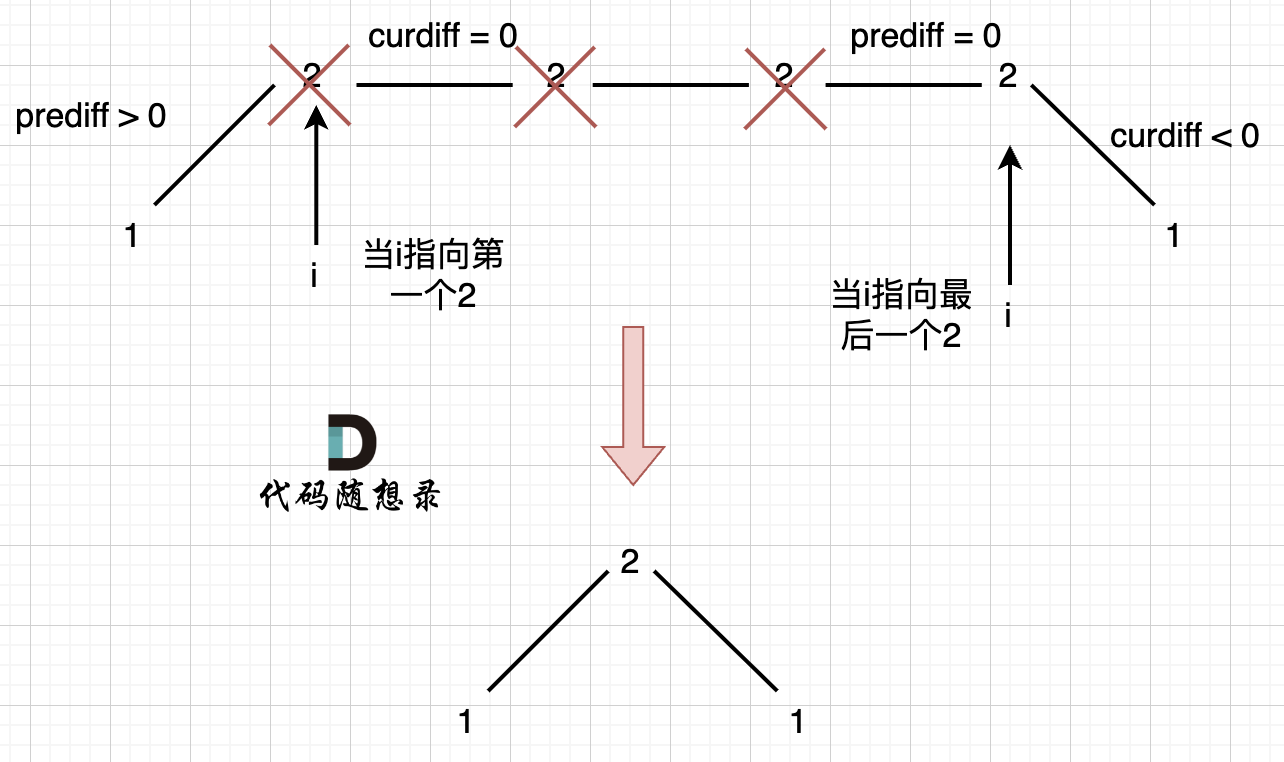
在图中，当i指向第一个2的时候，prediff > 0 && curdiff = 0 ，当 i 指向最后一个2的时候 prediff = 0 && curdiff < 0。
如果我们采用，删左面三个2的规则，那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值。

综合到上述：记录条件【prediff>=0 && curdiff<0 或 prediff=<0 && curdiff>0】

情况2：首尾两端

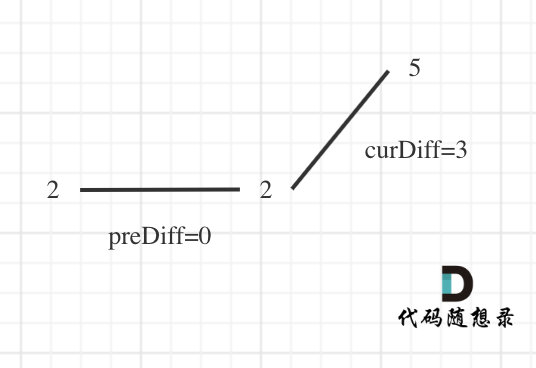
result初始为1（默认最右面有一个峰值），
curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）

做法：初始化prediff=0

情况3：单调有平坡

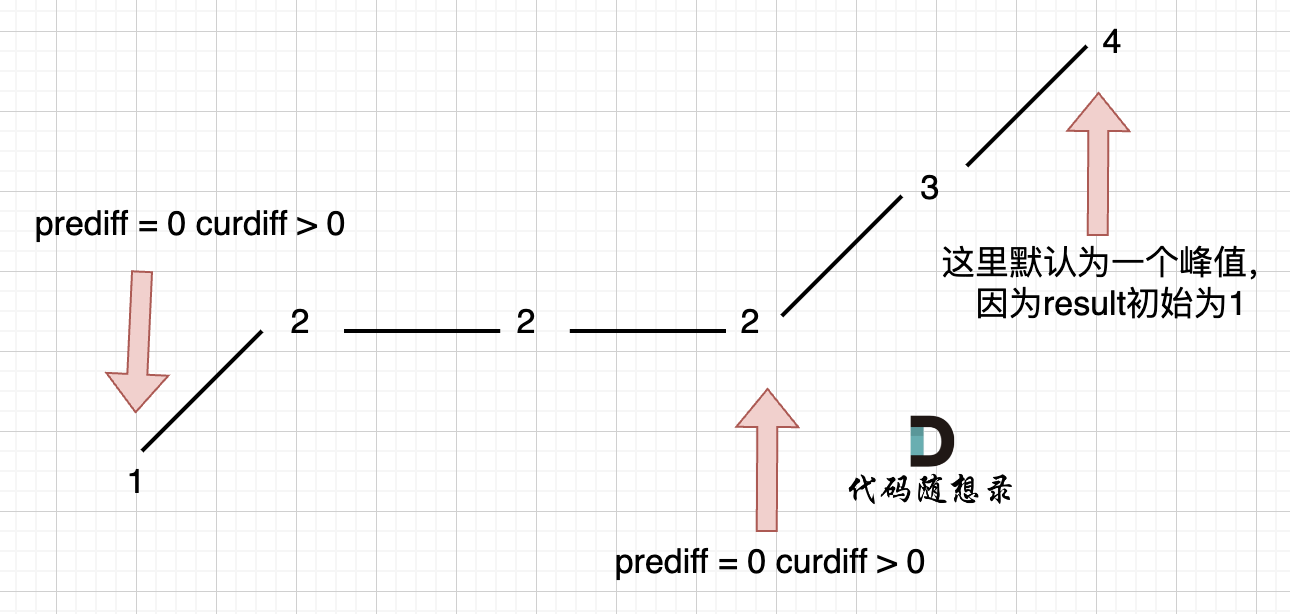
只需要在 这个坡度 摆动变化的时候，更新prediff就行，这样prediff在 单调区间有平坡的时候 就不会发生变化

做法：调整prediff更新位置

java实现

class Solution {
    public int wiggleMaxLength(int[] nums) {
    
        int prediff = 0;//考虑只有两个元素的时候，默认为0；为头元素制造一个平坡
        int curdiff = 0;
        int result = 1;//默认最右端有坡度
        //一个元素的时候
        if(nums.length == 0) return result;
        
        for(int i=0;i<nums.length-1;i++){//nums.length-1 因为最右端已经记录了

            curdiff = nums[i+1] - nums[i];
             
            if((prediff>=0 && curdiff <0) || (prediff<=0 && curdiff >0)){
                result++;
                prediff = curdiff;
            }
        //prediff = curdiff;
        }
        return result;
    }
}

股票问题---122. 买卖股票的最佳时机 II

只有一只股票！当前只有买股票或者卖股票的操作
关键点：想到其实最终利润是可以分解的：每天的利润
贪心：只收集每次的正利润

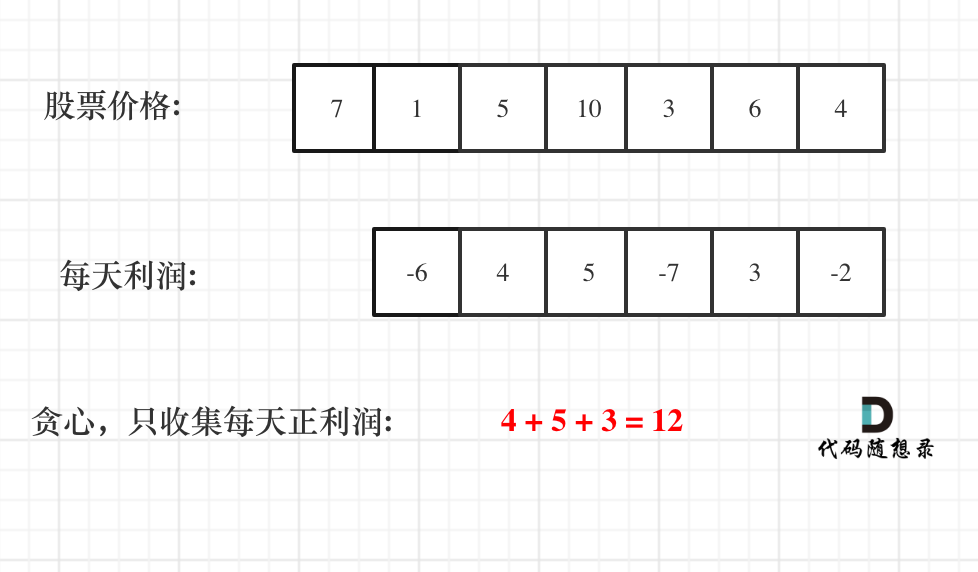
其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。

java

class Solution {
    public int maxProfit(int[] prices) {
        int sum = 0;
        for(int i=0;i < prices.length-1;i++){
            if((prices[i+1] - prices[i])>= 0){
                sum += prices[i+1] - prices[i];
            }
        }

        return sum;
    }
}

两个维度权衡问题---135. 分发糖果

关键点：两边分别考虑
先确定 右边比左边高的情况；然后再确定 左边比右边高的情况

class Solution {
    public int candy(int[] ratings) {
        int sum = 0;
        int len = ratings.length;
        int[] candy = new int[len];
        

        candy[0]=1;


        for(int i=1;i<len;i++){
            if(ratings[i] > ratings[i-1]){
                candy[i] = candy[i-1] +1;
            }else{
                candy[i] =1;
            }
        }

        for(int i=len-2;i>=0;i--){
            if(ratings[i] > ratings[i+1]){
                candy[i] = Math.max(candy[i+1] +1,candy[i]);
            }
        }

        for(int i=0;i<len;i++){
            sum += candy[i];
        }

        return sum;
    }
}