lec-5-Policy Gradients
直接策略微分
- Goal:
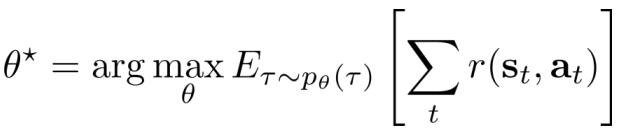
- idea:求最大值:直接求导
- tip:利用log导数等式进行变换
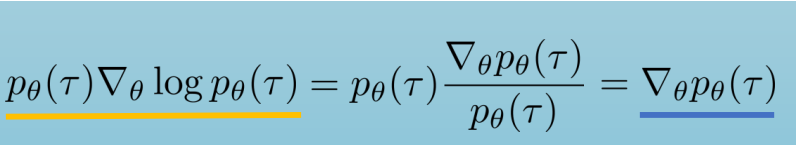
- 具体推导:
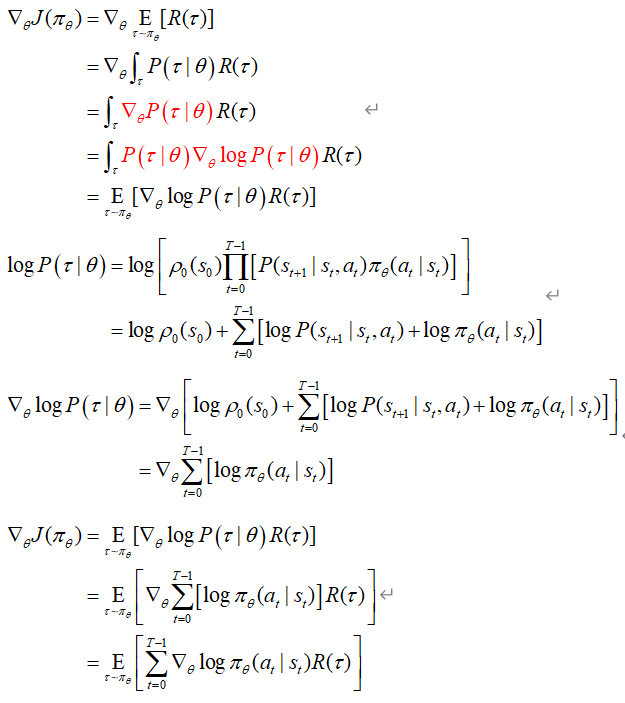
理解策略梯度
假定开始policy服从高斯分布,采样得到回报,计算梯度,根据reward增加动作概率,改变policy分布
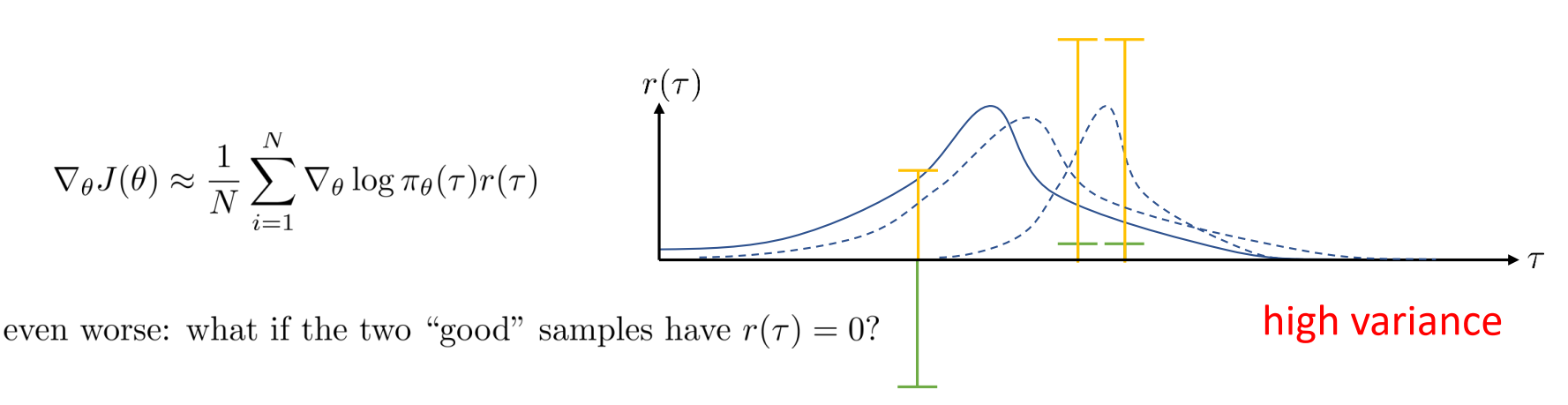
- 会发生的错误:高方差
- 当采样有负奖励样本的时候(绿色奖励),原本policy改变向右移动更多(最右边的虚曲线);改变奖励(添加常量),变为正奖励(黄色奖励),向右移动的少了(中间虚曲线),从而这导致了高差异(相比于之前的曲线)。
- 如果对于无限样本,不会导致差异。
- 如果回报为0,那么它们的policy梯度就不重要。
减少方差
- 因果关系:放弃过去的回报,policy不会影响t之前的回报
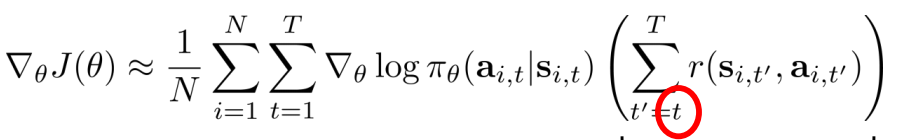
- Baselines:不会改变期望值,会改变方差
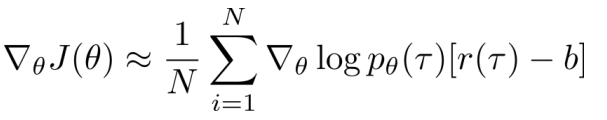
一般取b为回报均值: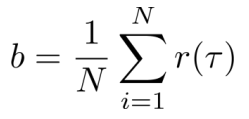 【but使得方差最小(即方差为0)的b不是回报均值】
【but使得方差最小(即方差为0)的b不是回报均值】
Off-policy PG
- REINFORCE algorithm(on-policy)
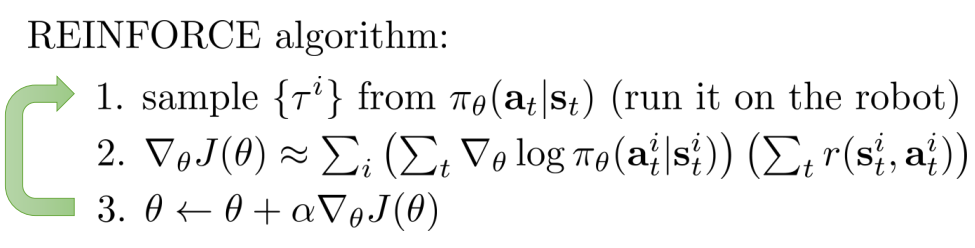
- 缺点:每次改进参数都要扔掉样本(样本利用率低);单步梯度更新
- 在基本RL过程中的表示:
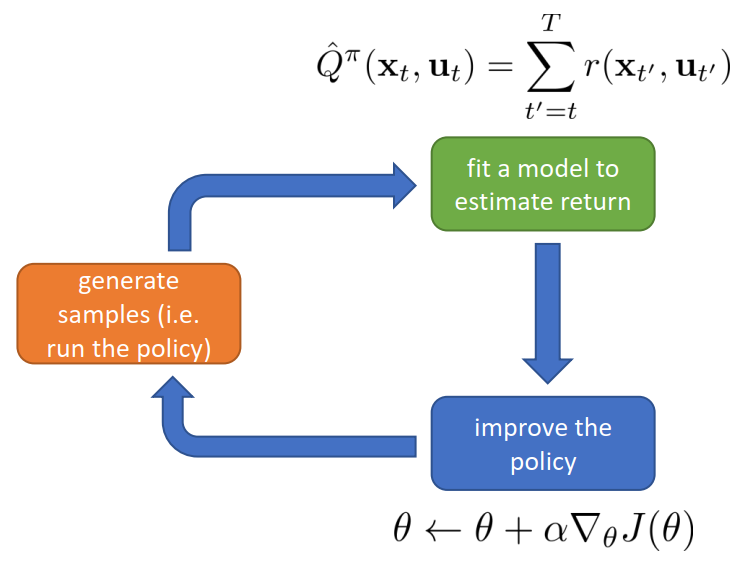
- 重要性采样原理(IS):实现从on-policy到off-policy
- 原理:

- 应用于RL:重用以前的policy(用 旧policy 进行采样,然后改进参数)
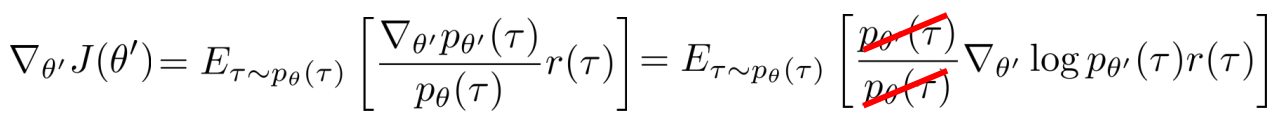
- 原理:
- 应用
- 使用自动差分器:伪loss进行反向传播
- 实际要考虑
- 梯度的高方差
- 批量学习batch size
- 学习率的调整learning rate
- 优化器的选择optimizers
Advanced PG
- 学习率的难题
policy参数服从高斯分布,梯度总会趋向于更小的方差的方向移动,方差就成了决定性因素,均值就不动了,梯度速度就慢了,继而收敛慢了。故学习率调整的难题,如果 速度小,学习率大,会使得policy在均值方向上很快不动。 - 自然梯度
- 自动步长调整
.....
Resource:CS285官网资料
版权归原作者 Lee_ing 所有
未经原作者允许不得转载本文内容,否则将视为侵权;转载或者引用本文内容请注明来源及原作者

