Canvas 实现灵动的红鲤鱼动画（上）

前言

上一篇文章《Canvas 仿百度贴吧客户端 loading 小球》实现了百度贴吧客户端的 loading 小球效果，同时还留下了一个任务：实现灵动的红鲤鱼动画。

这个动画效果实现起来比较难，需要良好的数学基础。而中学时学到的三角函数知识，早就还给数学老师了。现在一边练习一边写这篇文章，并不能保证最后能实现这个动画效果。

实现过程

第零步：绘制重心

画出鲤鱼的重心。为了方便看效果，以重心为原点，绘制了两条简单的坐标轴。

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <title>Title</title>
    <style>
        canvas {
            width: 500px;
            height: 500px;
            border: 1px solid #ccc;
        }
    </style>
</head>
<body>
<canvas id="canvas" width="500" height="500"></canvas>

<script>
    var canvas = document.getElementById('canvas')
    canvas.width = 500
    canvas.height = 500
    var ctx = canvas.getContext('2d')
    var width = canvas.width
    var height = canvas.height

    // 重心 middle point
    var mPt = {
        x: 250,
        y: 250
    }
    var R = 30 // 鱼头半径
    var angle = 0 // 鱼的角度

    // x 坐标
    ctx.fillStyle='#000'
    ctx.beginPath()
    ctx.moveTo(0, mPt.y)
    ctx.lineTo(width, mPt.y)
    ctx.stroke()

    // y 坐标
    ctx.beginPath()
    ctx.moveTo(mPt.x, 0)
    ctx.lineTo(mPt.x, height)
    ctx.closePath()
    ctx.stroke()

    function drawPt(pt) {
        ctx.fillStyle = '#000'
        ctx.beginPath()
        ctx.arc(pt.x, pt.y, 4, 0, 2 * Math.PI)
        ctx.fill()
    }
    
    // 重心
    drawPt(mPt)
</script>
</body>
</html>

第一步：绘制鱼头

首先需要求出鱼头的坐标。

先定义一个函数，能根据一个点的坐标，相对这个点的角度和距离，求出另一个点的坐标。

function getPt(pt, angle, length) {
    return {
        x: pt.x + length * Math.cos(angle * Math.PI / 180),
        y: pt.y - length * Math.sin(angle * Math.PI / 180)
    }
}

由于鱼头位于鱼前进方向，距离重心 1.5R 的位置，先求出鱼头的位置：

var headPt = getPt(mPt, angle, 1.5 * R) // 鱼头位置
drawPt(headPt)

然后以鱼头位置为圆心，半径为 R 的绘制圆形：

// 绘制鱼头
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(headPt.x, headPt.y, R, 0, 2 * Math.PI)
ctx.fill()

效果如下：

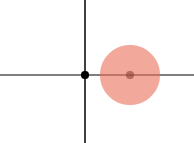
第二步：绘制鱼身

鱼身不是一个规则的图形，它是由两条直线和两条曲线组成的闭合路径。曲线可以用贝塞尔曲线绘制。

我们先绘制鱼左边的身体，首先需要求出左侧贝塞尔曲线的三个控制点：

从图可以看出，当鱼的角度为 0° 时，控制点 bodyLeft1 位于重心右方向 1.5R、上方向 R 的位置。

我写了一个函数，能根据 0° 时点的坐标求出任意度时点的坐标，源码如下。实现原理是，先求出该点距离重心的距离（鱼旋转时，该点距离重心的距离不变）和角度，再根据鱼的方向求出正确的位置。

function quickPt(pt) {
    var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
    var angl = getAngle(mPt, pt)
    return getPt(mPt, angle + angl, length)
}

function getAngle(cPt, pt) {
    var angl = Math.atan((cPt.y - pt.y) / (pt.x - cPt.x)) * 180 / Math.PI
    if (pt.y < cPt.y) {
        if (pt.x < cPt.x) {
            console.log('第二')
            angl = 90 + 90 + angl
        }
        if (pt.x > cPt.x) {
            console.log('第一')
        }
    } else if (pt.y > cPt.y) {
        if (pt.x < cPt.x) {
            console.log('第三')
            angl = 90 + 90 + angl
        }
        if (pt.x > cPt.x) {
            console.log('第四')
            angl = 360 + angl
        }
        if (pt.x === cPt.x) {
            angl = 270
        }
    } else {
        if (pt.x < cPt.x) {
            angl = 180
        }
    }
    return angl
}

这样的话，三个控制点的位置我们就可以轻易地求出来：

// 身体
var bodyLeft1 = quickPt({x: mPt.x + 1.5 * R, y: mPt.y - R})
drawPt(bodyLeft1)
var bodyLeft2 = quickPt({x: mPt.x, y: mPt.y - 1.5 * R})
drawPt(bodyLeft2)
var bodyLeft3 = quickPt({x: mPt.x - 1.5 * R, y: mPt.y - 0.8 * R})
drawPt(bodyLeft3)

效果如下：

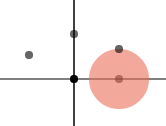
根据三个控制点绘制贝塞尔曲线：

ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(bodyLeft1.x, bodyLeft1.y)
ctx.quadraticCurveTo(bodyLeft2.x, bodyLeft2.y, bodyLeft3.x, bodyLeft3.y)
ctx.fill()

效果如下：

鱼右边的三个控制点和左边的三个控制点是对称的，再像前面那样求出坐标则显得啰嗦。所以，定义一个函数，能根据某一点的坐标，求出对称点的坐标，两点关于鱼身的中轴线对称。

// 获取对称坐标
function getSymmetricPt(pt) {
    var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
    var angl = getAngle(mPt, pt)
    return getPt(mPt, angle * 2 - angl, length)
}

原理是两点关于鱼的中轴线对称的话，这两点到重心的距离相等，并且两点与重心的连线与中轴线夹角相等。

因为 (angle1 + angle2) / 2 = angle，所以 angle2 = angle * 2 - angle1

有了这个函数，我们可以轻易求出鱼身体右侧三个控制点的坐标：

var bodyRight3 = getSymmetricPt(bodyLeft3)
drawPt(bodyRight3)
var bodyRight2 = getSymmetricPt(bodyLeft2)
drawPt(bodyRight2)
var bodyRight1 = getSymmetricPt(bodyLeft1)
drawPt(bodyRight1)

再通过三个控制点绘制贝塞尔曲线，最后用直线链接两个贝塞尔曲线，填充路径。

身体部分完整代码如下：

// 身体
var bodyLeft1 = quickPt({x: mPt.x + 1.5 * R, y: mPt.y - R})
drawPt(bodyLeft1)
var bodyLeft2 = quickPt({x: mPt.x, y: mPt.y - 1.5 * R})
drawPt(bodyLeft2)
var bodyLeft3 = quickPt({x: mPt.x - 1.5 * R, y: mPt.y - 0.8 * R})
drawPt(bodyLeft3)
var bodyRight3 = getSymmetricPt(bodyLeft3)
drawPt(bodyRight3)
var bodyRight2 = getSymmetricPt(bodyLeft2)
drawPt(bodyRight2)
var bodyRight1 = getSymmetricPt(bodyLeft1)
drawPt(bodyRight1)

ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(bodyLeft1.x, bodyLeft1.y)
ctx.quadraticCurveTo(bodyLeft2.x, bodyLeft2.y, bodyLeft3.x, bodyLeft3.y)
ctx.lineTo(bodyRight3.x, bodyRight3.y)
ctx.quadraticCurveTo(bodyRight2.x, bodyRight2.y, bodyRight1.x, bodyRight1.y)
ctx.closePath()
ctx.fill()

效果如下：

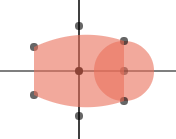
第三步：绘制鱼鳍

// 右鳍
var rightPt1 = getPt(headPt, angle - 110, 0.9 * R)
var rightPt2 = getPt(mPt, angle - 70, 4 * R)
var rightPt3 = getPt(mPt, angle - 90, 0.9 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(rightPt1.x, rightPt1.y)
ctx.quadraticCurveTo(rightPt2.x, rightPt2.y, rightPt3.x, rightPt3.y)
ctx.fill()

// 左鳍
var leftPt1 = getSymmetricPt(rightPt1)
var leftPt2 = getSymmetricPt(rightPt2)
var leftPt3 = getSymmetricPt(rightPt3)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(leftPt1.x, leftPt1.y)
ctx.quadraticCurveTo(leftPt2.x, leftPt2.y, leftPt3.x, leftPt3.y)
ctx.fill()

效果：

第四步：绘制鱼尾

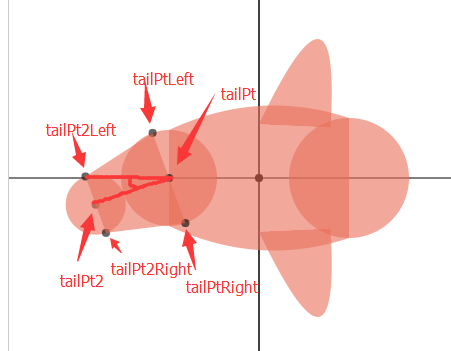
尾部的绘制是一个繁琐而又无味的过程。从上图可以看出，仅仅绘制尾部的前半部分，我们就需要求出 6 个点的坐标。尾部是可以摆动的，所以尾部并不是关于中轴线对称，而是与中轴线有一个偏角，我们定义这个偏角为 tailOffset。上图中，尾部的第一个圆半径为 TAIL_SIZE，即 0.8R；第二个圆半径为 TAIL_SIZE2，即 0.5R。

var TAIL_SIZE = 0.8
var TAIL_SIZE2 = 0.5
var tailOffset = 20

// 尾部
var tailPt = getPt(mPt, 180 + angle, 1.5 * R)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt.x, tailPt.y, TAIL_SIZE * R, 0, 2 * Math.PI)
ctx.fill()
drawPt(tailPt)

var tailPtLeft = getPt(tailPt, 180 + tailOffset - 90, TAIL_SIZE * R)
drawPt(tailPtLeft)
var tailPtRight = getPt(tailPt, 180 + tailOffset + 90, TAIL_SIZE * R)
drawPt(tailPtRight)

var tailPt2 = getPt(tailPt, 180 + angle + tailOffset, (TAIL_SIZE2 + TAIL_SIZE) * R)
drawPt(tailPt2)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt2.x, tailPt2.y, TAIL_SIZE2 * R, 0, 2 * Math.PI)
ctx.fill()

var tainPt2Left = getPt(tailPt2, 180 + tailOffset - 90, TAIL_SIZE2 * R)
drawPt(tainPt2Left)
var tailPt2Right = getPt(tailPt2, 180 + tailOffset + 90, TAIL_SIZE2 * R)
drawPt(tailPt2Right)

ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPtLeft.x, tailPtLeft.y)
ctx.lineTo(tainPt2Left.x, tainPt2Left.y)
ctx.lineTo(tailPt2Right.x, tailPt2Right.y)
ctx.lineTo(tailPtRight.x, tailPtRight.y)
ctx.fill()

效果：

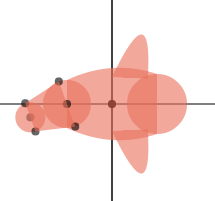
继续绘制鱼尾的后半部分，上图：

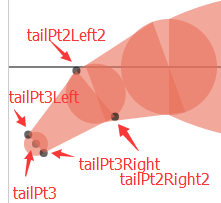
继续无聊的求点连线。。。

var TAIL_SIZE3 = 0.2

var tailPt3 = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1.3 * R)
drawPt(tailPt3)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.arc(tailPt3.x, tailPt3.y, TAIL_SIZE3 * R, 0, 2 * Math.PI)
ctx.fill()

var tainPt2Left2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE2 * R)
drawPt(tainPt2Left2)
var tailPt2Right2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE2 * R)
drawPt(tailPt2Right2)

var tainPt3Left = getPt(tailPt3, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE3 * R)
drawPt(tainPt3Left)
var tailPt3Right = getPt(tailPt3, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE3 * R)
drawPt(tailPt3Right)

ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tainPt2Left2.x, tainPt2Left2.y)
ctx.lineTo(tainPt3Left.x, tainPt3Left.y)
ctx.lineTo(tailPt3Right.x, tailPt3Right.y)
ctx.lineTo(tailPt2Right2.x, tailPt2Right2.y)
ctx.fill()

绘制第一个三角形

var triangleCenter = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 0.8 * R)
drawPt(triangleCenter)
var triangleLeft = getPt(triangleCenter, 180 + tailOffset + tailOffset2 - 90, 0.6 * R)
drawPt(triangleLeft)
var triangleRight = getPt(triangleCenter, 180 + tailOffset + tailOffset2 + 90, 0.6 * R)
drawPt(triangleRight)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPt2.x, tailPt2.y)
ctx.lineTo(triangleLeft.x, triangleLeft.y)
ctx.lineTo(triangleRight.x, triangleRight.y)
ctx.fill()

效果：

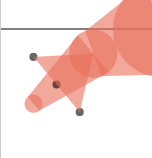
绘制第二个三角形：

var triangle2Center = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1 * R)
drawPt(triangle2Center)
var triangle2Left = getPt(triangle2Center, 180 + tailOffset + tailOffset2 - 90, 0.8 * R)
drawPt(triangle2Left)
var triangle2Right = getPt(triangle2Center, 180 + tailOffset + tailOffset2 + 90, 0.8 * R)
drawPt(triangle2Right)
ctx.fillStyle = '#ea6f5a'
ctx.beginPath()
ctx.moveTo(tailPt2.x, tailPt2.y)
ctx.lineTo(triangle2Left.x, triangle2Left.y)
ctx.lineTo(triangle2Right.x, triangle2Right.y)
ctx.fill()

效果：

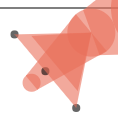
第五步：删除多余的点和线

删除所有 drawPt 代码和坐标轴，就大功告成了！

效果：

总结

虽然最后绘制出了鲤鱼，但这条死气沉沉的鲤鱼显然不够灵动。下一篇，会在模仿的基础上加点小创新，实现更加灵动的小鲤鱼。

参考

《自定义Drawable实现灵动的红鲤鱼动画（上篇）》

附录

附上完整代码：

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <title>Title</title>
    <style>
        canvas {
            width: 500px;
            height: 500px;
            border: 1px solid #ccc;
        }
    </style>
</head>
<body>
<canvas id="canvas" width="500" height="500"></canvas>

<script>
    var canvas = document.getElementById('canvas')
    canvas.width = 500
    canvas.height = 500
    var ctx = canvas.getContext('2d')
    var width = canvas.width
    var height = canvas.height

    // 重心 middle point
    var mPt = {
        x: 250,
        y: 250
    }
    var R = 30 // 鱼头半径
    var angle = 0 // 鱼的角度

    function drawPt(pt) {
        ctx.fillStyle = '#000'
        ctx.beginPath()
        ctx.arc(pt.x, pt.y, 4, 0, 2 * Math.PI)
        ctx.fill()
    }

    function getPt(pt, angle, length) {
        return {
            x: pt.x + length * Math.cos(angle * Math.PI / 180),
            y: pt.y - length * Math.sin(angle * Math.PI / 180)
        }
    }

    function quickPt(pt) {
        var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
        var angl = getAngle(mPt, pt)
        return getPt(mPt, angle + angl, length)
    }

    function getAngle(cPt, pt) {
        var angl = Math.atan((cPt.y - pt.y) / (pt.x - cPt.x)) * 180 / Math.PI
        if (pt.y < cPt.y) {
            if (pt.x < cPt.x) {
                //console.log('第二')
                angl = 90 + 90 + angl
            }
            if (pt.x > cPt.x) {
                //console.log('第一')
            }
        } else if (pt.y > cPt.y) {
            if (pt.x < cPt.x) {
                //console.log('第三')
                angl = 90 + 90 + angl
            }
            if (pt.x > cPt.x) {
                //console.log('第四')
                angl = 360 + angl
            }
            if (pt.x === cPt.x) {
                angl = 270
            }
        } else {
            if (pt.x < cPt.x) {
                angl = 180
            }
        }
        return angl
    }

    // 获取对称坐标
    function getSymmetricPt(pt) {
        var length = Math.sqrt((pt.x - mPt.x) * (pt.x - mPt.x) + (pt.y - mPt.y) * (pt.y - mPt.y))
        var angl = getAngle(mPt, pt)
        return getPt(mPt, angle * 2 - angl, length)
    }

    ctx.globalAlpha = '0.6'

    var headPt = getPt(mPt, angle, 1.5 * R) // 鱼头位置

    // 绘制鱼头
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.arc(headPt.x, headPt.y, R, 0, 2 * Math.PI)
    ctx.fill()

    // 身体
    var bodyLeft1 = quickPt({x: mPt.x + 1.5 * R, y: mPt.y - R})
    var bodyLeft2 = quickPt({x: mPt.x, y: mPt.y - 1.5 * R})
    var bodyLeft3 = quickPt({x: mPt.x - 1.5 * R, y: mPt.y - 0.8 * R})
    var bodyRight3 = getSymmetricPt(bodyLeft3)
    var bodyRight2 = getSymmetricPt(bodyLeft2)
    var bodyRight1 = getSymmetricPt(bodyLeft1)

    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(bodyLeft1.x, bodyLeft1.y)
    ctx.quadraticCurveTo(bodyLeft2.x, bodyLeft2.y, bodyLeft3.x, bodyLeft3.y)
    ctx.lineTo(bodyRight3.x, bodyRight3.y)
    ctx.quadraticCurveTo(bodyRight2.x, bodyRight2.y, bodyRight1.x, bodyRight1.y)
    ctx.closePath()
    ctx.fill()

    // 右鳍
    var rightPt1 = getPt(headPt, angle - 110, 0.9 * R)
    var rightPt2 = getPt(mPt, angle - 70, 4 * R)
    var rightPt3 = getPt(mPt, angle - 90, 0.9 * R)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(rightPt1.x, rightPt1.y)
    ctx.quadraticCurveTo(rightPt2.x, rightPt2.y, rightPt3.x, rightPt3.y)
    ctx.fill()

    // 左鳍
    var leftPt1 = getSymmetricPt(rightPt1)
    var leftPt2 = getSymmetricPt(rightPt2)
    var leftPt3 = getSymmetricPt(rightPt3)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(leftPt1.x, leftPt1.y)
    ctx.quadraticCurveTo(leftPt2.x, leftPt2.y, leftPt3.x, leftPt3.y)
    ctx.fill()

    var TAIL_SIZE = 0.8
    var TAIL_SIZE2 = 0.4
    var TAIL_SIZE3 = 0.15
    var tailOffset = 20
    var tailOffset2 = 20

    // 尾部
    var tailPt = getPt(mPt, 180 + angle, 1.5 * R)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.arc(tailPt.x, tailPt.y, TAIL_SIZE * R, 0, 2 * Math.PI)
    ctx.fill()

    var tailPtLeft = getPt(tailPt, 180 + tailOffset - 90, TAIL_SIZE * R)
    var tailPtRight = getPt(tailPt, 180 + tailOffset + 90, TAIL_SIZE * R)

    var tailPt2 = getPt(tailPt, 180 + angle + tailOffset, (TAIL_SIZE2 + TAIL_SIZE) * R)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.arc(tailPt2.x, tailPt2.y, TAIL_SIZE2 * R, 0, 2 * Math.PI)
    ctx.fill()

    var tainPt2Left = getPt(tailPt2, 180 + tailOffset - 90, TAIL_SIZE2 * R)
    var tailPt2Right = getPt(tailPt2, 180 + tailOffset + 90, TAIL_SIZE2 * R)

    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(tailPtLeft.x, tailPtLeft.y)
    ctx.lineTo(tainPt2Left.x, tainPt2Left.y)
    ctx.lineTo(tailPt2Right.x, tailPt2Right.y)
    ctx.lineTo(tailPtRight.x, tailPtRight.y)
    ctx.fill()

    var tailPt3 = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1.3 * R)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.arc(tailPt3.x, tailPt3.y, TAIL_SIZE3 * R, 0, 2 * Math.PI)
    ctx.fill()

    var tainPt2Left2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE2 * R)
    var tailPt2Right2 = getPt(tailPt2, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE2 * R)

    var tainPt3Left = getPt(tailPt3, 180 + tailOffset + tailOffset2 - 90, TAIL_SIZE3 * R)
    var tailPt3Right = getPt(tailPt3, 180 + tailOffset + tailOffset2 + 90, TAIL_SIZE3 * R)

    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(tainPt2Left2.x, tainPt2Left2.y)
    ctx.lineTo(tainPt3Left.x, tainPt3Left.y)
    ctx.lineTo(tailPt3Right.x, tailPt3Right.y)
    ctx.lineTo(tailPt2Right2.x, tailPt2Right2.y)
    ctx.fill()

    var triangleCenter = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 0.8 * R)
    var triangleLeft = getPt(triangleCenter, 180 + tailOffset + tailOffset2 - 90, 0.6 * R)
    var triangleRight = getPt(triangleCenter, 180 + tailOffset + tailOffset2 + 90, 0.6 * R)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(tailPt2.x, tailPt2.y)
    ctx.lineTo(triangleLeft.x, triangleLeft.y)
    ctx.lineTo(triangleRight.x, triangleRight.y)
    ctx.fill()

    var triangle2Center = getPt(tailPt2, 180 + angle + tailOffset + tailOffset2, 1 * R)
    var triangle2Left = getPt(triangle2Center, 180 + tailOffset + tailOffset2 - 90, 0.8 * R)
    var triangle2Right = getPt(triangle2Center, 180 + tailOffset + tailOffset2 + 90, 0.8 * R)
    ctx.fillStyle = '#ea6f5a'
    ctx.beginPath()
    ctx.moveTo(tailPt2.x, tailPt2.y)
    ctx.lineTo(triangle2Left.x, triangle2Left.y)
    ctx.lineTo(triangle2Right.x, triangle2Right.y)
    ctx.fill()
</script>
</body>
</html>

posted @ 2017-08-05 22:30 yunser_blog 阅读(1168) 评论(2) 编辑收藏举报

刷新页面返回顶部

yunser

Canvas 实现灵动的红鲤鱼动画（上）

前言

实现过程

总结

参考

附录

公告