PCA实现教程

数据是机器学习模型的生命燃料。对于特定的问题，总有很多机器学习技术可供选择，但如果没有很多好的数据，问题将不能很好的解决。数据通常是大部分机器学习应用程序中性能提升背后的驱动因素。

有时，数据可能很复杂。在那么多的数据中，知道哪些数据是真正重要的，具有一定的挑战性。降维是一种可以帮助我们更好地了解数据的技术，它减少了数据集的特征数量，因此只剩下最重要的部分特征。

主成分分析（PCA）是一种用于降维的简单而强大的技术。通过它，我们可以直接减少特征变量的数量，从而减少重要特征并节省计算量。从高层次来看，PCA有三个主要步骤：

（1）计算数据的协方差矩阵；

（2）计算该协方差矩阵的特征值和向量；

（3）通过特征值和向量来只选择最重要的特征向量，然后将数据转换为这些向量以降低维度。

（1）计算协方差矩阵

PCA产生一个特征子空间，使特征向量的方差最大化。因此，为了正确计算这些特征向量的方差，必须对它们进行适当的平衡。为实现此目的，我们首先将数据归一化为零均值和单位方差，以便在计算中对每个特征进行加权。假设我们的数据集为X：

 

from sklearn.preprocessing import StandardScaler
   X = StandardScaler().fit_transform(X)

 

两个变量的协方差衡量它们是如何“相关”的。如果两个变量的协方差是正的，那么当一个变量增加时，另一个变量增加；在协方差为负的情况下，特征变量的值将在相反方向上改变。协方差矩阵只是一个数组，其中每个值基于矩阵中的x-y位置指定两个特征变量之间的协方差。公式是：

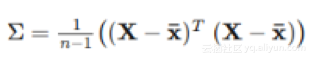
其中带有上划线的x是X的每个特征的均值向量，将转置矩阵乘以原始矩阵时，我们最终将每个数据点的每个特征相乘！在numpy代码中实现如下：

 

import numpy as np
# Compute the mean of the data
mean_vec = np.mean(X, axis=0)
# Compute the covariance matrix
cov_mat = (X - mean_vec).T.dot((X - mean_vec)) / (X.shape[0]-1)
# OR we can do this with one line of numpy:
cov_mat = np.cov(X.T)

 

（2）计算特征值和向量

我们的协方差矩阵的特征向量（主成分）表示新特征空间的向量方向，而特征值表示这些向量的大小。由于我们正在研究协方差矩阵，因此特征值量化了每个向量的贡献方差。

如果特征向量具有相应的高幅度特征值，则意味着我们的数据在特征空间中沿着该向量具有高方差。因此，该向量包含有关数据的大量信息，因为沿着该向量的任何移动都会导致大的“方差”。另一方面，具有小特征值的向量具有低方差，因此当沿着该向量移动时，我们的数据不会有很大变化。由于在沿着特定特征向量移动时没有任何变化，即改变该特征向量的值不会对我们的数据产生很大影响，那么我们可以说这个特征不是很重要，可以忽略它。

这是PCA中特征值和向量的全部本质，找到表示数据最重要的向量，并丢弃其余的向量。计算协方差矩阵的特征向量和值是一个简单的单线性的numpy。之后，我们将根据它们的特征值按降序对特征向量进行排序。

 

# Compute the eigen values and vectors using numpy
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)

 

（3）映射到新的向量上

此时，我们有一个特征向量列表，这些特征向量基于它们的特征值按照数据集的“重要性”进行排序。现在要做的是选择最重要的特征向量并丢弃其余的，可以通过查看向量的可解释方差百分比来巧妙地做到这一点。该百分比量化了总100％中每个主成分可归因于多少信息（方差）。

我们举一个例子来说明。假设一个最初有10个特征向量的数据集。在计算协方差矩阵之后，特征值是：

[12,10,8,7,5,1,0.1,0.03,0.005,0.0009]

该数组的总和= 43.1359，但前6个值代表：43 / 43.1359 =总数的99.68％！这意味着我们的前6个特征向量有效地保持了99.68％有关数据集的信息。因此，可以丢弃最后4个特征向量，因为它们只包含0.32％的信息，这就节省了40%的计算量。

因此，我们可以简单地定义一个阈值，这个阈值可以决定是保留还是丢弃每个特征向量。在下面的代码中，设定阈值97%来决定每个特征向量是否丢弃。

 

# Only keep a certain number of eigen vectors based on 
# the "explained variance percentage" which tells us how 
# much information (variance) can be attributed to each 
# of the principal components

exp_var_percentage = 0.97 # Threshold of 97% explained variance
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
num_vec_to_keep = 0
for index, percentage in enumerate(cum_var_exp):
  if percentage > exp_var_percentage:
    num_vec_to_keep = index + 1
    break

 

最后一步是将我们的数据实际投射到决定保留的向量上。我们通过构建投影矩阵来做到这一点：我们将通过相乘将数据投影到新的向量上。为了创建它，简单地与决定保留的所有特征向量进行连接，最后一步是简单地在原始数据和投影矩阵之间取点积。

维度降低了！

 

# Compute the projection matrix based on the top eigen vectors
num_features = X.shape[1]
proj_mat = eig_pairs[0][1].reshape(num_features,1)
for eig_vec_idx in range(1, num_vec_to_keep):
  proj_mat = np.hstack((proj_mat, eig_pairs[eig_vec_idx][1].reshape(num_features,1)))
# Project the data 
pca_data = X.dot(proj_mat)

 

原文链接
本文为云栖社区原创内容，未经允许不得转载。