线性模型之线性回归

线性回归：

\(h_\theta (x) = \theta_0 + \theta_1x_1+\cdots + \theta_nx_n = X\theta\)
假设函数\(h_\theta (x)\)为\(m+1\)的向量。\(\theta\)为\((n+1)*1\)的向量，里边有n+1个代数的模型参数，\(X\)为\(m*(n+1)\)的矩阵

最大似然估计

原理： 概率大的事件在一次观测中更容易发生；在一次观测中发生了的事件其概率应该大
目标：寻找能够以较高概率产生观察数据的系统发生树

推导

\(y^{(i)} = \theta^Tx^{(i)} + \epsilon ^{(i)}\)

• \(y^{(i)}\) ：第i个标签值
• \(x^{(i)}\) ：第i个样本
• \(\theta^Tx^{(i)}\): 在当前\(\theta\)下,第i个样本预测值
• \(\epsilon ^{(i)}\) ：在当前\(\theta\)下，预测值和实际值的误差

1. 误差\(\epsilon ^{(i)}(1\leq i \leq n)\)是独立同分布的，服从均值为 0，方差为\(\sigma^2\)的高斯分布（中心极限定理）
2. 实际问题中，很多随机现象可以看成众多因素的独立影响的综合反映，往往服从正态分布

高斯分布：\(p(x)=\frac{1}{\sigma\sqrt{ 2\pi}}e^{-\frac{(x-u)^2}{2\sigma^2}}\)

第一步：对于第i个样本

• \(p(\epsilon^{(i)})=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(\epsilon^{(i)})^2}{2\sigma^2}}\)
• \(p(y^{(i)}|x^{(i)};\theta)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}}\)

第二步：似然函数：

• \(L(\theta) =\prod^m_{i=1}p(y^{(i)}|x^{(i)};\theta) = \prod^m_{i=1}\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}}\)
  第三步：取对数（取对数并不影响极值，且简化计算）：

• \(l(\theta)=logL(\theta)\)
  =\(log\prod^m_{i=1}\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}}\)

  = \(\sum^m_{i=1}log\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}}\)

  = \(\sum_{i=1}^mlog\frac{1}{\sigma \sqrt{2\pi}}-\frac{1}{\sigma^2}\cdot{\frac{1}{2}}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2\)

第四步：欲使\(l(\theta)\)最大，使\({\frac{1}{2}}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2\)最小即可。原因：\(\sigma\)是误差的方差，是定值。

损失函数\(loss(y,\hat{y})=J(\theta)={\frac{1}{2}}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2\)

• \(y^{(i)}\) ：第i个标签值
• \(x^{(i)}\) ：第i个样本
• \(\theta\) ：模型要学习的变量，目的使损失函数最小

第六步：求解方法1（最小二乘法），令导数等于0：
\(J(\theta)={\frac{1}{2}}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2 = \frac{1}{2}(X\theta -Y)^T(X\theta -Y)\) --> \(min_\theta J(\theta)\)
\(\nabla_\theta J(\theta)=\nabla_\theta(\frac{1}{2}(X\theta -Y)^T(X\theta -Y))\)
= \(\nabla_\theta(\frac{1}{2}(\theta^TX^T -Y^T)(X\theta -Y))\)
= \(\nabla_\theta(\frac{1}{2}(\theta^TX^TX\theta -\theta^TX^TY -Y^TX\theta -Y^TY))\)
= \(\frac{1}{2}(2X^TX\theta -X^TY -(Y^TX)^T -Y^TY)\)
= \(X^TX\theta -X^TY\)

情况一：如果\(X^TX\)可逆=> \(\theta=(X^TX)^{-1}X^TY\)

此处推导用到的知识点

$(XY)^T=Y^TX^T$

$\frac{d(u^Tv)}{dx} = \frac{du^t}{dx}\cdot v + \frac{dv^T}{dx}\cdot u$

$\frac{\partial AX}{\partial X} = A^T$

$\frac{\partial AX}{\partial X^T} =\frac{\partial AB^T}{\partial B} = A$

$\frac{\partial X^TA}{\partial X} =\frac{\partial A^TX}{\partial X} =(A^T)^T = A$

$\frac{\partial X^TX}{\partial X} = \frac{\partial X^T \cdot{(X)}}{\partial X} + \frac{ \partial (X^T)\cdot{} X}{\partial X} = 2X$

$\frac{\partial X^TAX}{\partial X} = \frac{\partial X^T \cdot{(AX)}}{\partial X} + \frac{ \partial (X^TA)\cdot{} X}{\partial X} = AX+A^TX$

----- 若A为对称阵，则有$\frac{\partial X^TAX}{\partial X} =2AX$

$\frac{\partial A^TXB}{\partial X} = (BA^T)^T=AB^T$

$\frac{\partial A^TX^TXA}{\partial X} = AXA + A^TX^TA^T= XA^TA + XAA^T=2XAA^T$

$\frac{\partial |A|}{\partial A} =|A|(A^{-1})^T$

情况二：实际上因为特征数量大于样本数量等原因，\(X^TX\)常常不可逆，可以增加额外的数据，导致最终的矩阵可逆=> \(\theta=(X^TX +\lambda I)^{-1}X^TY\) （岭回归的解为上述公式：\(J(\theta)={\frac{1}{2}}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2 + \lambda \sum_{j=1}^{n}\theta^2_j\)）

python 实现

import numpy as np
def standRegres(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T * xMat 
    if np.linalg.det(xTx) == 0.0:
        print('矩阵行列式为0，不可逆')
        return
    ws = xTx.I * (xMat.T * yMat)
    return ws

第五步：求解方法2，梯度下降法，逼近全局（局部）最优解：

梯度下降法

目标函数\(\theta\)求解：
\(J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2\)

• \(h_{\theta}(x^{(i)})：第i个预测值\)
• \(y^{(i)}：第i个标签值\)

原理：沿着负梯度方向迭代，更新后的\(\theta\)使\(J(\theta)\)更小
迭代公式：\(\theta = \theta - \alpha \cdot \frac{\partial J(\theta)}{\partial \theta}\)

• \(\alpha\) :学习率、步长

梯度方向：

• \(\frac{\partial J(\theta)}{\partial \theta_j} =\frac{\partial \frac{1}{2}(h_\theta(x) -y)^2}{\partial \theta_j}\)
  = \((h_\theta(x)-y)\cdot\frac{\partial(\sum_{i=1}^m\theta_ix_i-y)}{\partial\theta_j}\)
  = \((h_\theta(x)-y)x_j\)

更新第j个\(\theta\)：
\(\theta_j=\theta_j +\alpha\sum^m_{i=1}(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}\)

批量梯度下降法（BGD）

for j=1 to n:
\(\theta_j=\theta_j +\alpha\sum^m_{i=1}(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}\)

import numpy as np
# 假设空间函数：h(x)
def xTx (xArr):
    xMat = np.mat(xArr)
    return xMat.T * xMat

# alpha：学习率 maxCycle：学习的迭代次数 
def gradAscent (dataMatin,labels, alpha=0.1, maxCycle=100):
    
    dataMatrix= np.mat(dataMatin)
    labelsMatrix = np.mat(labels).T 
    m,n = np.shape(dataMatrix)
    # 初始化权重
    weights = np.ones((n,1))
    for k in maxCycle:
        # error, dataMatrix 为m*n的矩阵
        error = labelsMatrix - xTx(dataMatrix *weights)
        weights = weights + alpha * dataMatrix.T * error
    return weight

随机梯度下降法（SGD）

for j=1 to n:
\(\theta_j=\theta_j +\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}\)

• 与批量梯度下降法主要体现在权重不同

import numpy as np
# 假设空间函数：h(x)
def xTx (xArr):
    xMat = np.mat(xArr)
    return xMat.T * xMat

# alpha：学习率 maxCycle：学习的迭代次数 
def gradAscent (dataMatin,labels, alpha=0.1):
    
    dataMatrix= np.mat(dataMatin)
    labelsMatrix = np.mat(labels).T 
    m,n = np.shape(dataMatrix)
    # 初始化权重
    weights = np.ones((n,1))
    for i in range(m):
        # error, dataMatrix 为m*n的矩阵
        error = labelsMatrix[i] - xTx(dataMatrix[i] * weights)
        weights = weights + alpha * error * dataMatrix[i]
    return weights

改进：alpha = 4/(i+j) + 0.01 缓解随机梯度下降法的数据波动或高频波动，常数项的目的是保持alpha不等于0
小批量梯度下降法（MBGD）省略

BGD、SGD和MBGD的比较

• SGD速度比BGD快（迭代次数少）
• SGD在有多个局部局部最优解时，可能跳出某些局部最优解，所以不会比BGD坏
• BGD一定可以得到一个局部最优解，SGD由于随机性可能结果比BGD差
• 当样本量为m的时候，每次迭代BGD算法中对于参数值更新一次，SGD算法中对于参数值更新m次，MBGD算法中对于参数值更新m/n次，相对来讲SGD算法的更新速度最快
• SGD算法中对于每个样本都需要更新参数值，当样本值不太正常的时候，就有可能会导致本次的参数更新会产生相反的影响，也就是说SGD算法的结果并不是完全收敛的，而是在收敛结果处波动的
• SGD算法是每个样本都更新一次参数值，所以SGD算法特别适合样本数据量大的情况以及在线机器学习(Online ML)。

梯度下降法调优策略

• 学习率：大则变化大，可能跳过最优解，小则变化小，时间长
• 初始值选择：初始值不同，得到的结果可能不同；一般情况多次运行，选择损失函数最小的结果值
• 标准化：由于样本的取值范围不同，可能导致在各个参数上迭代速度不同，一般将特征标准化

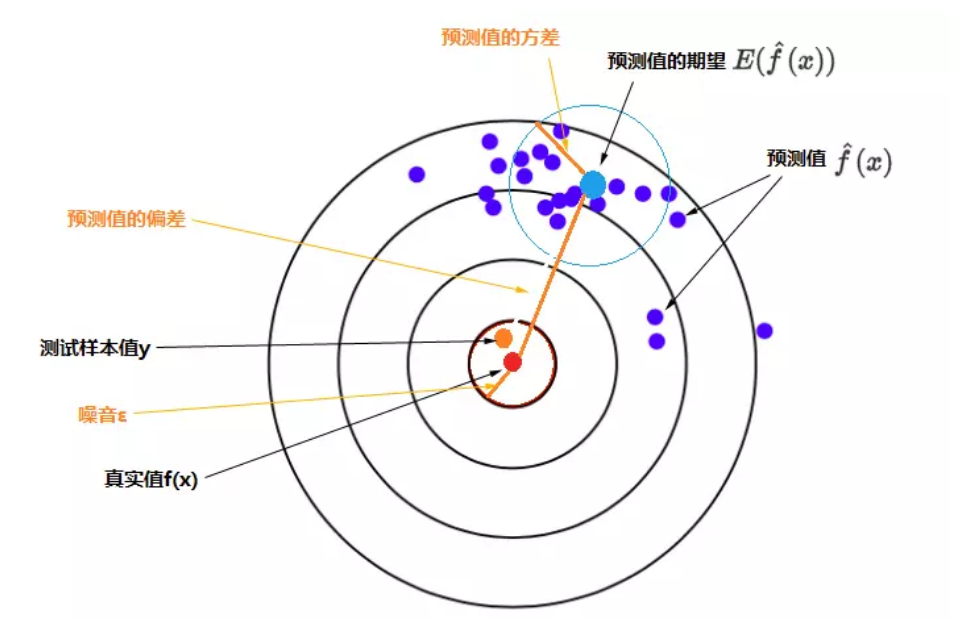
偏差（Bias）和方差(Variance)

对于监督模型可以采用平方误差函数度量：即\(y-\hat{y}(x)^2\)

• y:标签值
• \(\hat{y}\)：模型（函数）

\(E(y-\hat{y}(x)^2)=\Sigma^2+Var[\hat{f}(x)]+(Bias[\hat{f}(x)])^2\)

即：误差的期望值 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值的偏差的平方

• 偏差：度量了学习算法的期望与真实数据偏离的水平，即学习算法本身的拟合程度
• 方差：度量了同样大小的训练集的变动所导致的学习性能上的变化，即刻画了数据扰动所造成的影响
• 噪音：表达了在当前任务上任何学习算法所达到的期望误差的下界，，即刻画了学习问题本身的难度

推导过程暂略

欠拟合

减少欠拟合方法：

1. 增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间;
2. 增加模型复杂度：尝试非线性模型，比如核SVM 、决策树、DNN等模型;
3. 如果有正则项可以较小正则项参数 ;
4. Boosting ,Boosting 往往会有较小的 Bias，比如 Gradient Boosting 等.

局部回归算法

线性回归求得是具有最小无偏估计，所以可能欠拟合。所以可以在估计中引入偏差，降低预测的均方误差

• 普通线性回归损失函数：

  \(J(\theta) = \sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^{2}\)

• 局部加权回归损失函数：

  \(J(\theta) = \sum^m_{i=1} w^{(i)}(h_{\theta}(x^{(i)}) - y^{(i)})^{2}\)

• \(w^{(i)}\) 是权重，根据要预测的点与数据集中的点的距离来为数据集中的点赋权值。当某点离要预测的点越远，其权重越小，否则越大。常用备选公式：

  \(w^{(i)} = exp(-\frac{( x^{(i)}-\overline{x})^2}{2k^2})\)

• 该函数被称为指数衰减函数，其中 k 为波长系数，它控制了权值随距离下降的速率

• 主意：使用该方式主要应用到样本之间的相似性考虑，主要内容在 SVM 中考虑（核函数）

import numpy as np
def lwlr(testpoint,xArr, yArr,k=0.1):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    m,n = np.shape(xMat)
    weights = np.mat(np.eye(m))
    for j in range(m):
        diffMat = testpoint - xMat[j:]
        weight[j,j]= np.exp(diffMat * diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if np.linalg.det(xTx) == 0.0:
        print('矩阵行列式为0，不可逆')
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testpoint * ws
# 给空间一点，计算出对应的回归系数估计
lwlr(xArr[0],xArr,yArr,0.001)

过拟合

解决过拟合的方法：

1. 交叉检验，通过交叉检验得到较优的模型参数;
2. 特征选择，减少特征数或使用较少的特征组合，对于按区间离散化的特征，增大划分的区间;
3. 正则化，常用的有 L1、L2 正则。而且 L1正则还可以自动进行特征选择;
4. 如果有正则项则可以考虑增大正则项参数 lambda;
5. 增加训练数据可以有限的避免过拟合;
6. Bagging ,将多个弱学习器Bagging 一下效果会好很多，比如随机森林等.
7. 降低模型复杂度：在数据较少时，降低模型复杂度是比较有效的方法，适当的降低模型复杂度可以降低模型对噪声的拟合度。神经网络中可以减少网络层数，减少神经元个数，dropout；决策树可以控制树的深度，剪枝等。

正则项

L1,L2正则化，正则化就是在目标函数里面添加参数惩罚项，用来控制模型的复杂度，正则化项可以降低模型的权重值，L1会产生稀疏解，L2会产生缩放效应整体压缩权重值，从而控制模型复杂度，根据奥卡姆剃刀原理，拟合效果差不多情况下，模型复杂度越低越好。

L1和L2稀疏解的不同：

角度1，解空间：

• 原函数：

  • \(min\sum_{i=1}^N(y_i-w^Tx_i)^2\)
  • \(s.t.||w||_2^2<m\)

• 拉格朗日函数：

  • \(\sum_{i=1}^N(y_i-w^Tx_i)^2+\lambda(||w||_2^2-m)\)

• 对偶函数和原函数的最优解\(\lambda^*\)和\(w^*\)满足：

  • \(0=\nabla_w(\sum_{i=1}^N(y_i-w^{*T}x_i)^2+\lambda^*(||w^*||_2^2-m))\)
  • \(0\leq\lambda^*\)

• L2正则化相当于给参数定义了圆形的解空间（L2范式小于等于m）

• L1正则化相当于给参数定义了“菱角分明”的解空间，更容易出现稀疏解

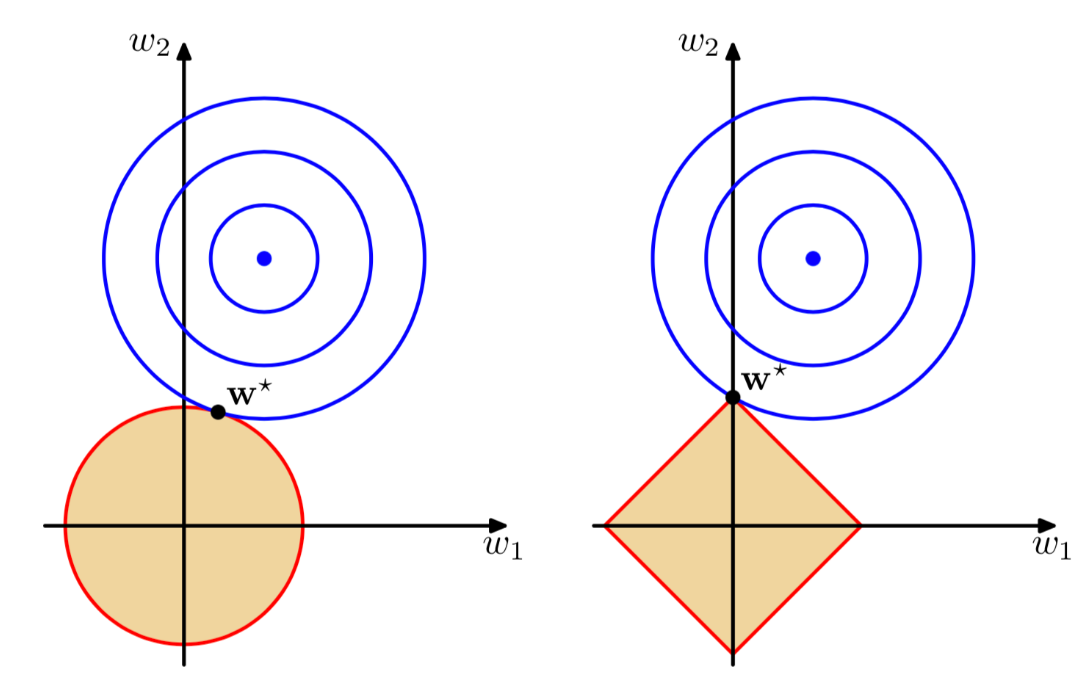
角度2：函数叠加：
角度3：贝叶斯先验：

• L1正则相当于给参数w引入了拉普拉斯先验，拉普拉斯分布中参数w取值为0的可能性更高
• L2正则相当于高斯先验，高斯分布认为在w在极值点附件取不同值的可能性是相同的
  • 拉普拉斯分布在0值附近突出；而高斯分布在0值附近分布平缓

Ridge 回归

• 使用 L2 正则的线性回归模型就称为 Ridge 回归（岭回归）

\(J(\theta) = \frac{1}{2}\sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^{2} + \lambda \sum^n_{i=1} \theta^2_j \quad \quad \lambda >0\)

Lasso 回归

• 使用 L1 正则的线性回归模型就称为 Lasso 回归

  \(J(\theta) = \frac{1}{2}\sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^{2} + \lambda \sum^n_{i=1} |\theta_j | \quad \quad \lambda > 0\)

Elasitc Net

• 同时使用 L1 正则和 L2 正则的线性回归模型就称为 Elasitc Net（算法）

  \(J(\theta) = \frac{1}{2}\sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^{2} + \lambda p \sum^n_{i=1} |\theta_j | + \lambda (1-p)\sum^n_{i=1} \theta^2_j \quad \quad \lambda > 0，p\in [0，1]\)

模型效果判断

• MSE：误差平方和，越趋近于0表示模型越拟合训练数据,受异常值影响较大
• RMSE：MES的平方根，作用同MSE
• \(R^2\)：取值范围(负无穷,1]，值越大表示模型越拟合训练数据；最优解是1；当模型预测为随机值的时候，有可能为负；若预测值恒为样本期望，\(R^2\)为0
• TSS：总平方和TSS（Total Sum of Squares，表示样本之间的差异情况，是伪方差的m倍
• RSS：残差平方和RSS，表示预测值与样本值之间的差异情况，是MSE的m倍