利用Hough变换识别图像中的直线

引入

近期看到2015年数学建模A题太阳影子定位中的第四问，需要根据附件中视频里的直杆的太阳影子的变化确定拍摄地点。其实确定拍摄地点这个问题并不是十分困难，因为有前三问的铺垫，我们已经得出了太阳影子长度和观测地点的经纬度、时间、直杆高度四个参数之间的关系；所以我们只要知道了直杆太阳影子的长度就可以通过问题2中的优化模型求解出拍摄地点的经纬度了。但是本题难就难在，如何确定视频中直杆的太阳影子的长度？

求解

首先想到的是：将视频处理后，能否通过手动标示像素点来确定直杆的太阳影子的长度，因为可以手动标示的工具较多，如AE中的动态跟踪、PS中的像素点提取、Matlab里的ginput。虽然可以有效的解决直杆的太阳影子长度的测量，但是笔者认为这种人工手动测量的方法的误差较高，且逐个进行测量特别麻烦，且误差可能不够大。不符合笔者比较懒得性格，所以在这里给出自己的一种解法

1.视频的逐分提取

这部分比较简单。

2图像的预处理

图像二值化处理。

3.通过Hough变换

Hough变换是图像处理中从图像识别几何形状的方法。它利用点与线的对偶性，将原始图像空间的给定曲线通过曲线表达形式变为Hough参数空间中的一个点。所以原始图像给定曲线的检测问题就转化为在Hough参数空间的峰值问题，即检测整体特性转化为检测局部特性[7]。
欧式空间中一条直线上的点在Hough参数空间中为一条正弦曲线；欧式空间中同一条直线上的多个点在Hough参数空间中为一个正弦曲线簇且曲线簇相交于一点，称此点为峰值点。而Hough参数空间下的峰值点，则对应了欧式空间下的一条直线。
如图所示，

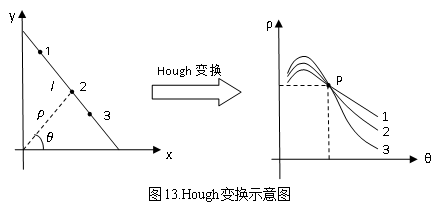
直线l方程为：

\[xcosθ+ysinθ=ρ \]

在欧式空间中数据点的表示为(x,y),而在Hough参数空间内表示为(ρ,θ),P点即为Hough参数空间中的峰值点，它所表示的含义即为欧式空间的l直线。
下面给出Hough变换的算法：
（1）初始并网格化Hough参数空间
（2）对于欧氏空间中的每个(x,y)执行步骤3；
（3）for θ=-90° to 180°，执行ρ=xcosθ+ysinθ与H(ρ,θ)=H(ρ,θ)+1
（4）设立阈值，寻找参数空间的峰值点。参数空间每一个峰值点对应欧式空间中一条直线。

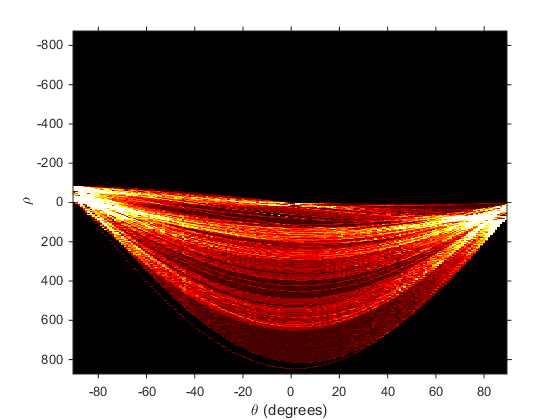
其中每一个网格颜色代表能量高低，颜色越亮表明能量越高，反之能量越低。能量越高的地方，即为所需求解的峰值点。得到峰值点后，通过编程反变换到原图像的RGB值空间中，即可识别出峰值点所对应的直线；直杆影子图像所检测出的直线如图所示：

已知直杆的高度\(h_真\)为2m，通过Hough变换得到了直杆的像素高度\(h_像\)为664.9218像素，同样直杆影子长度\(L_真\)通过Hough变换得到的直杆影子像素长度\(L_像\)为一组像素数据，根据比例关系：

\[\frac{L_真}{L_像}=\frac{h_真}{h_像}$$可以计算出直杆影子的真实长度。 \]