迷宫回溯算法(递归练习)

1:迷宫问题：

　　　用一个7 x 8的矩形表示迷宫,其中 1表示障碍物，2表示走过的路，3表示走过的路(走不通为3),通过设计编写程序设置起点达到终点的的路线:

          

 

 

 

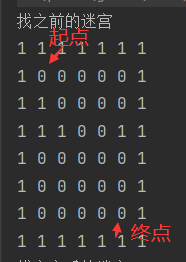
2:思路:

• 先画出迷宫(二维数组模拟)
• 设置一些路障(数组模拟即可)
• 制定路径决策 自由选择路径 可以先下->右->上->左;(可以自己设置进行优化)

3:实现:

• 制作迷宫与路障:

  public static void main(String[] args) {
          /*
          思路 地图的创建 其中 1表示障碍物，2表示走过的路，3表示走过的路(走不通为3)
          决策 自由选择路径 可以先下->右->上->左;(可以自己设置进行优化)
          决策不同 对应的路径也不同，
          这边迷宫是 7行8列
           */
          int[][] map = new int[8][7];
          //设置一个框 地图的建立 四周用1包围
          for (int i = 0; i < 7; i++) {
              map[0][i] = 1;
              map[7][i] = 1;
          }
          for (int i = 0; i < 8; i++) {
              map[i][0] = 1;
              map[i][6] = 1;
          }
          //这边是设置障碍物的位置
          map[3][1] = 1;
          map[3][2] = 1;
          map[2][1] =1;
          map[3][5]=1;
          //输出迷宫
          System.out.println("找之前的迷宫");
          getArray(map);
          //进行找路
          setWay(map,1,1);
          System.out.println("找完之后的迷宫");
          getArray(map);
      }

   

• 路径策略实现方法:

  /**
       * @param map 迷宫 
       * @param i   开始位置
  　   *　我们这边策略是 下,右,上,左
       * @param j   
       * @return 
       */
      public static boolean setWay(int map[][], int i, int j) {
          if (map[6][5] == 2) {//递归 先考虑出递归的情况 即是达到了map[6,5]这个位置
              return true;
          } else {
              if (map[i][j] == 0) {//注意这里是map[i][j]没有走过
                  map[i][j] = 2;//假设他可以走，那么
                  if (setWay(map, i+1, j)){
                      return true;//先走下
                  }
                  else if (setWay(map, i, j + 1)){
                      return true;//然后右
                  }
                  else if (setWay(map, i-1, j)){
                      return true;//然后上边
                  }
                  else if (setWay(map, i, j-1)){
                      return true;//然后走左
                  }
                  else {
                      //不能走就标记为3并且返回false
                      map[i][j] = 3;
                      return false;
                  }
              } else {
               //该点为 1或2或3，无法走通，直接返回上个方法（即上个点）
                   return false;
              }
          }
      }            

   

• 打印输出迷宫方法:

  //输出方法  
   public static void getArray(int[][]map){
          for (int i = 0; i < map.length; i++) {
              for (int j = 0; j < map[i].length; j++) {
                  System.out.print(map[i][j] + " ");
              }
              System.out.println();
          }
      }

• 最后结果:

        　　

    记录一下数据结构学习