MySQL -- 索引

本文转载自MySQL -- 索引

索引模型

哈希表

实现上类似于java.util.HashMap，哈希表适合只有等值查询的场景
img

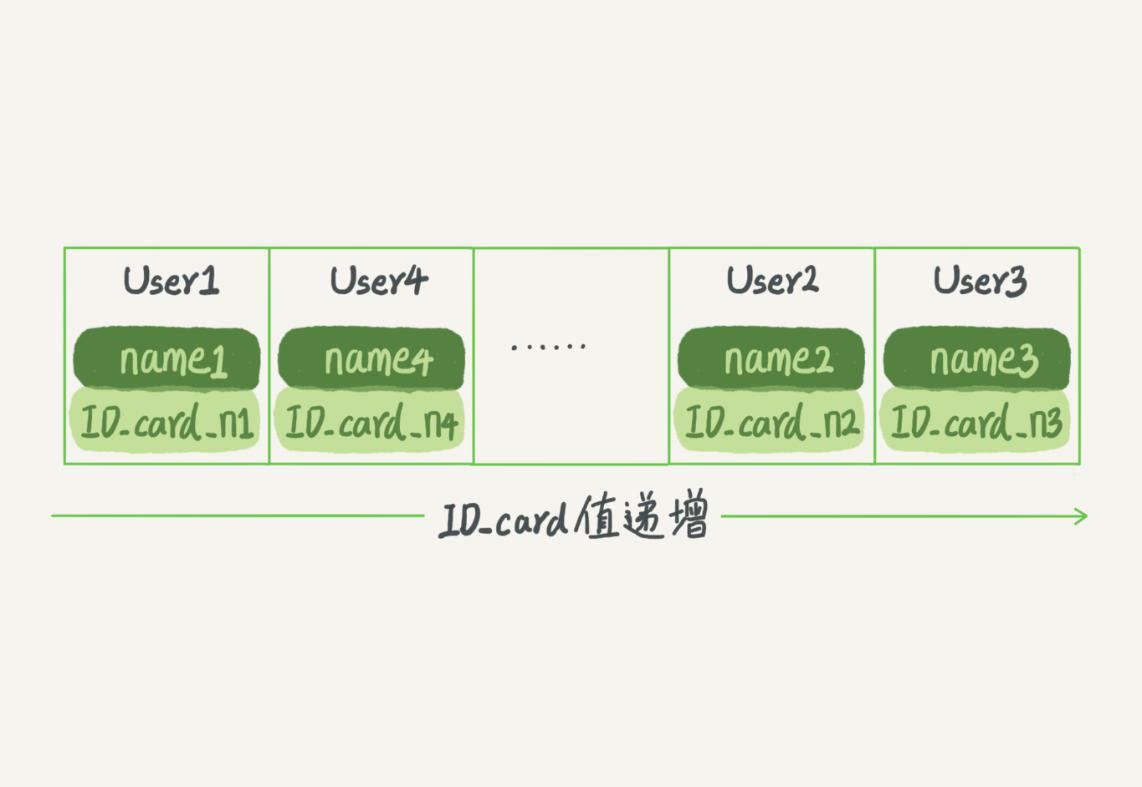
有序数组

有序数组只适用于静态存储引擎（针对不会再修改的数据）
img

查找

  1. 等值查询：可以采用二分法，时间复杂度为O(log(N))
  2. 范围查询：查找[ID_card_X,ID_card_Y]
    • 首先通过二分法找到第一个大于等于ID_card_X的记录
    • 然后向右遍历，直到找到第一个大于ID_card_Y的记录

更新

在中间插入或删除一个纪录就得挪动后面的所有的记录

搜索树

平衡二叉树

查询的时间复杂度：O(log(N))，更新的时间复杂度：O(log(N))（维持树的平衡）
img

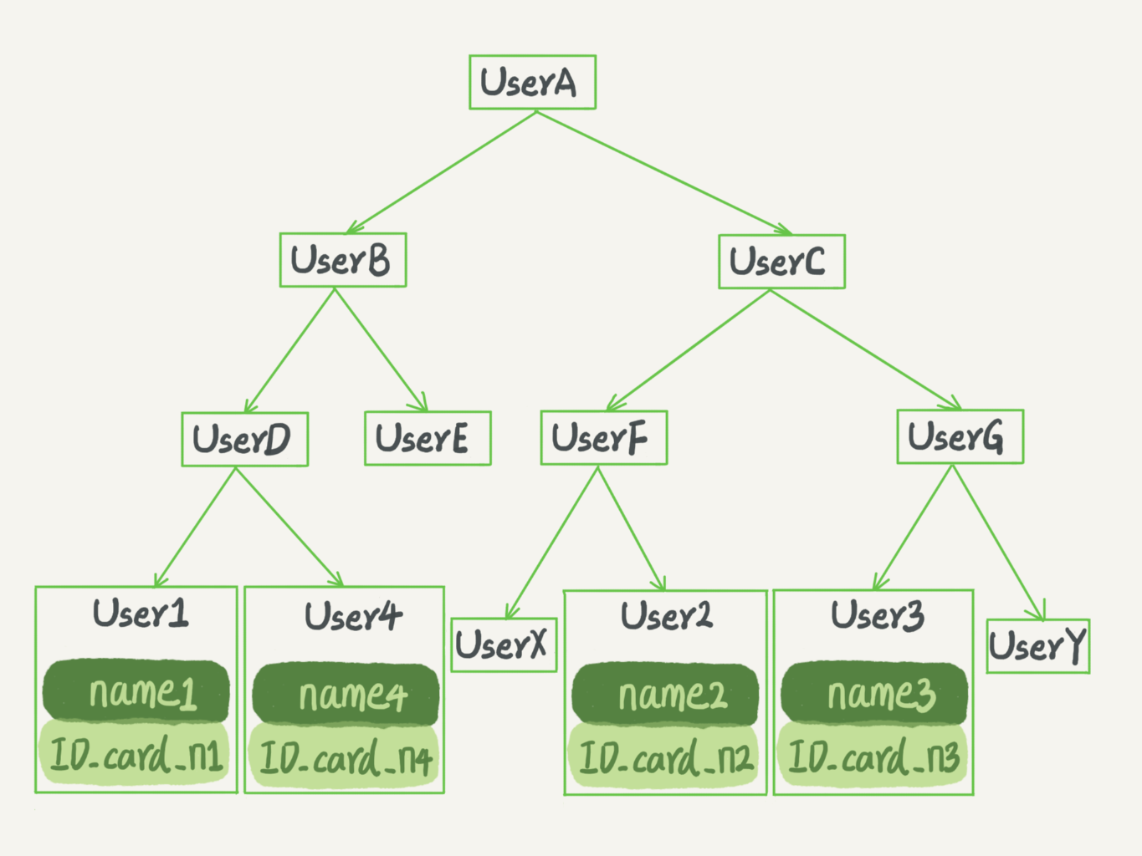
N叉树

  1. 大多数的数据库存储并没有采用二叉树，原因：索引不仅仅存在于内存中，还要写到磁盘上

    • 对于有100W节点的平衡二叉树，树高为20，即一次查询可能需要访问20个数据块
    • 假设HDD，随机读取一个数据块需要10ms左右的寻址时间
    • 即一次查询可能需要200ms – 慢成狗

  2. 为了让一个查询
    尽量少的读取磁盘，就必须让查询过程访问尽量少的数据块，因此采用N叉树

    • N的大小取决于数据页的大小和索引大小
    • 在InnoDB中，以INT（4 Bytes）字段为索引，假设页大小为16KB，并采用Compact行记录格式，N大概是745
    • 假设树高还是4（树根的数据块总是在内存中），数据量可以达到745^3 = 4.1亿
    • 访问这4亿行的表上的INT字段索引，查找一个值最多只需要读取3次磁盘（很大概率，树的第2层也在内存中）

  3. N叉树由于在读写上的性能优点以及适配HDD的访问模式，被广泛应用于数据库引擎中

InnoDB的索引

索引是在存储引擎层实现的，没有统一的索引标准，不同存储引擎的索引的工作方式是不一样的，哪怕多个存储引擎支持同一类型的索引，其底层的实现也可能不同的

索引组织表

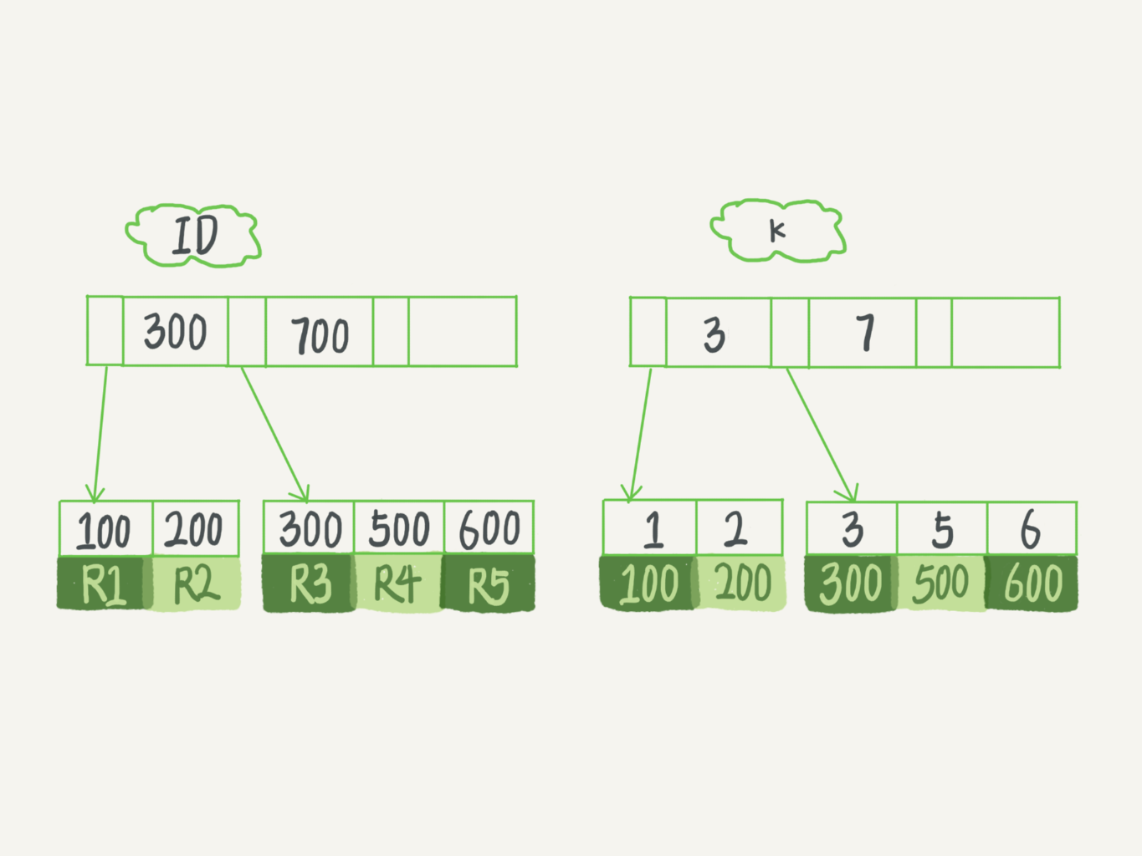
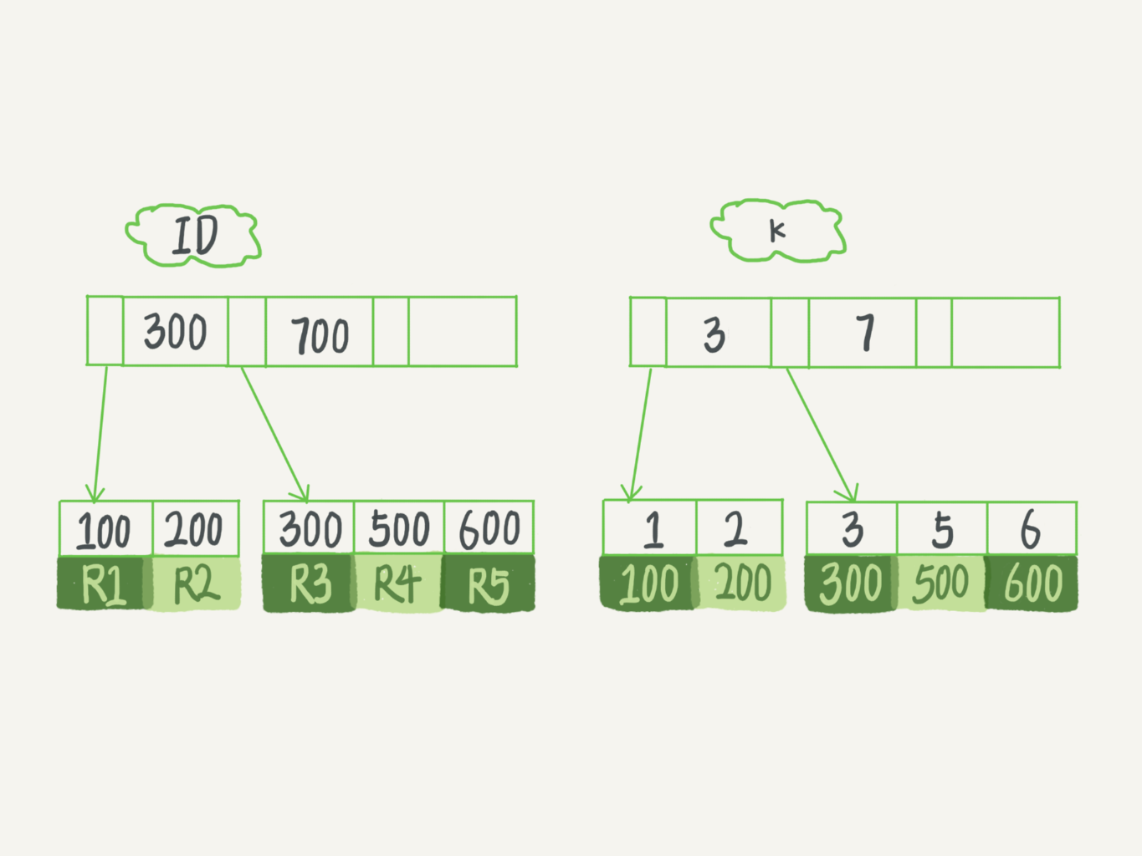
表都是根据主键顺序以索引的形式存放的，这种存储方式称为索引组织表，每一个索引在InnoDB里面都对应一棵B+树

# 建表
CREATE TABLE T(
    id INT PRIMARY KEY,
    k INT NOT NULL,
    INDEX (k)
) ENGINE=INNODB;

# 初始化数据
R1 : (100,1)
R2 : (200,2)
R3 : (300,3)
R4 : (500,5)
R5 : (600,6)

img

  1. 根据叶子节点的内容 ，索引类型分为聚簇索引clustered index）和二级索引（secondary index）

    • 聚簇索引的叶子节点存储的是整行数据
    • 二级索引的叶子节点存储的是主键的值

  2. select * from T where ID=500：只需要搜索ID树

  3. select * from T where k=5：先搜索k树，得到ID的值为500，再到ID树搜索，该过程称为回表

  4. 基于二级索引的查询需要多扫描一棵索引树，因此尽量使用主键查询

维护索引

  1. B+树为了维护索引的有序性，在插入新值时，需要做必要的维护

  2. 如果新插入的行ID为700，只需要在R5的记录后插入一个新纪录

  3. 如果新插入的行ID为400，需要逻辑上（实际采用链表的形式，直接追加）挪动R3后面的数据，空出位置

    • 如果R5所在的数据页已经满了，根据B+树的算法，需要申请一个新的数据页，然后将部分数据挪过去，称为页分裂
    • 页分裂的影响：性能、数据页的利用率

  4. 页合并 ：页分裂的逆过程

    • 当相邻两个页由于删除了数据，利用率很低之后，会将数据页合并

自增主键

  1. 逻辑：如果主键为自增，并且在插入新纪录时不指定主键的值，系统会获取当前主键的最大值+1作为新纪录的主键
    • 适用于递增插入的场景，每次插入一条新纪录都是追加操作，既不会涉及其他记录的挪动操作，也不会触发页分裂
  2. 如果采用业务字段作为主键，很难保证有序插入，写数据的成本相对较高
  3. 主键长度越小，二级索引占用的空间也就越小
    • 在一般情况下，创建一个自增主键，这样二级索引占用的空间最小
  4. 针对实际中一般采用分布式ID生成器的情况
    • 满足有序插入
    • 分布式ID全局唯一
  5. 适合直接采用业务字段做主键的场景：KV场景（只有一个唯一索引）
    • 无须考虑二级索引的占用空间问题
    • 无须考虑二级索引的回表问题

重建索引

# 重建二级索引
ALTER TABLE T DROP INDEX k;
ALTER TABLE T ADD INDEX(k);

# 重建聚簇索引
ALTER TABLE T DROP PRIMARY KEY;
ALTER TABLE T ADD PRIMARY KEY(id);
  1. 重建索引的原因
    • 索引可能因为删除和页分裂等原因，导致数据页有空洞
    • 重建索引的过程会创建一个新的索引，把数据按顺序插入
    • 这样页面的利用率最高，使得索引更紧凑，更省空间
  2. 重建二级索引k是合理的，可以达到省空间的目的
  3. 重建聚簇索引是不合理的
    • 不论是删除聚簇索引还是创建聚簇索引，都会将整个表重建
    • 替代语句：ALTER TABLE T ENGINE=INNODB

索引优化

覆盖索引

# 建表
CREATE TABLE T (
    ID INT PRIMARY KEY,
    k INT NOT NULL DEFAULT 0,
    s VARCHAR(16) NOT NULL DEFAULT '',
    INDEX k(k)
) ENGINE=INNODB;

# 初始化数据
INSERT INTO T VALUES (100,1,'aa'),(200,2,'bb'),(300,3,'cc'),(500,5,'ee'),(600,6,'ff'),(700,7,'gg');

img

需要回表的查询

SELECT * FROM T WHERE k BETWEEN 3 AND 5
  1. 在k树上找到k=3的记录，取得ID=300
  2. 再到ID树上查找ID=300的记录，对应为R3
  3. 在k树上取下一个值k=5，取得ID=500
  4. 再到ID树上查找ID=500的记录，对应为R4
  5. 在k树上取下一个值k=6，不满足条件，循环结束

整个查询过程读了k树3条记录，回表了2次

不需要回表的查询

SELECT ID FROM T WHERE k BETWEEN 3 AND 5

  1. 只需要查ID的值，而ID的值已经在k树上，可以直接提供查询结果，不需要回表

    • 因为k树已经覆盖了我们的查询需求，因此称为覆盖索引

  2. 覆盖索引可以减少树的搜索次数，显著提升查询性能，因此使用覆盖索引是一个常用的性能优化手段

  3. 扫描行数

    • 在存储引擎内部使用覆盖索引在索引k上其实是读取了3个记录，
    • 但对于MySQL的Server层来说，存储引擎返回的只有2条记录，因此MySQL认为扫描行数为2

联合索引

CREATE TABLE `tuser` (
    `id` INT(11) NOT NULL,
    `id_card` VARCHAR(32) DEFAULT NULL,
    `name` VARCHAR(32) DEFAULT NULL,
    `age` INT(11) DEFAULT NULL,
    `ismale` TINYINT(1) DEFAULT NULL,
    PRIMARY KEY (`id`),
    KEY `id_card` (`id_card`),
    KEY `name_age` (`name`,`age`)
) ENGINE=InnoDB

高频请求：根据id_card查询name。可以建立联合索引(id_card,name)，达到覆盖索引的效果

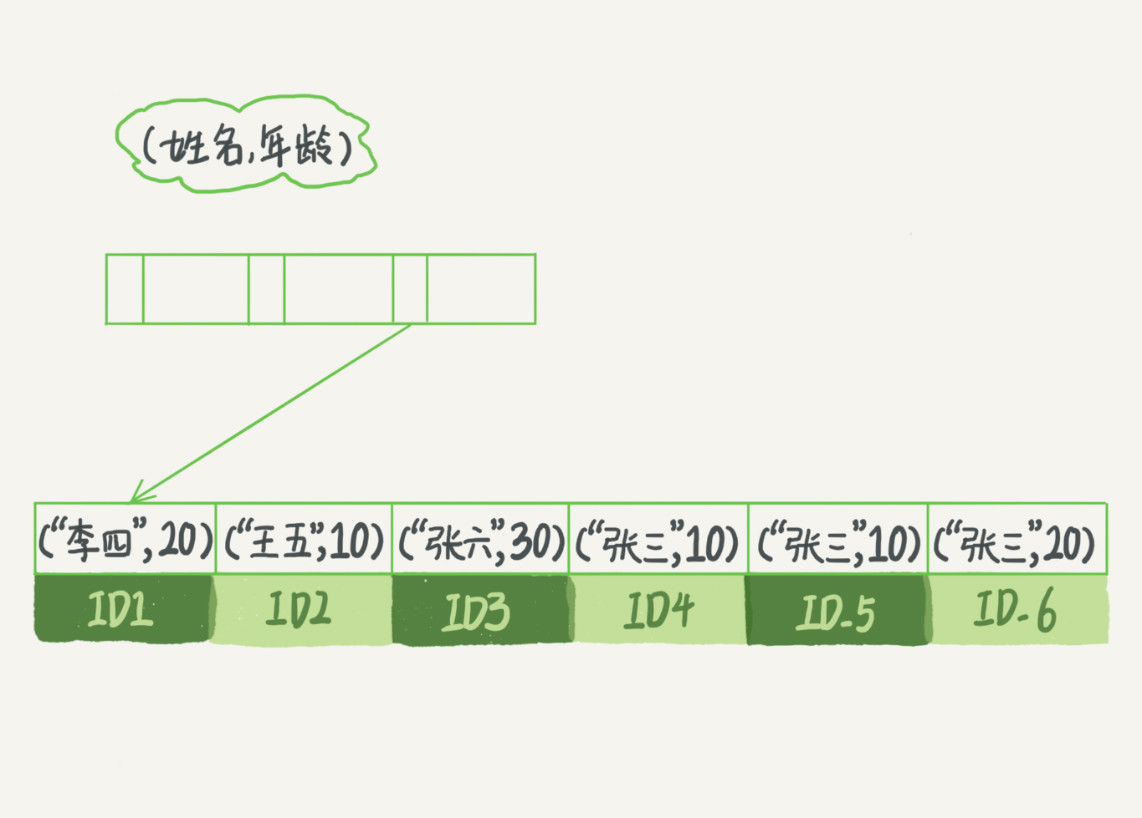
最左前缀原则

B+树的索引结构，可以利用索引的最左前缀来定位记录
img

  1. 索引项是按照索引定义里字段出现的顺序来排序的

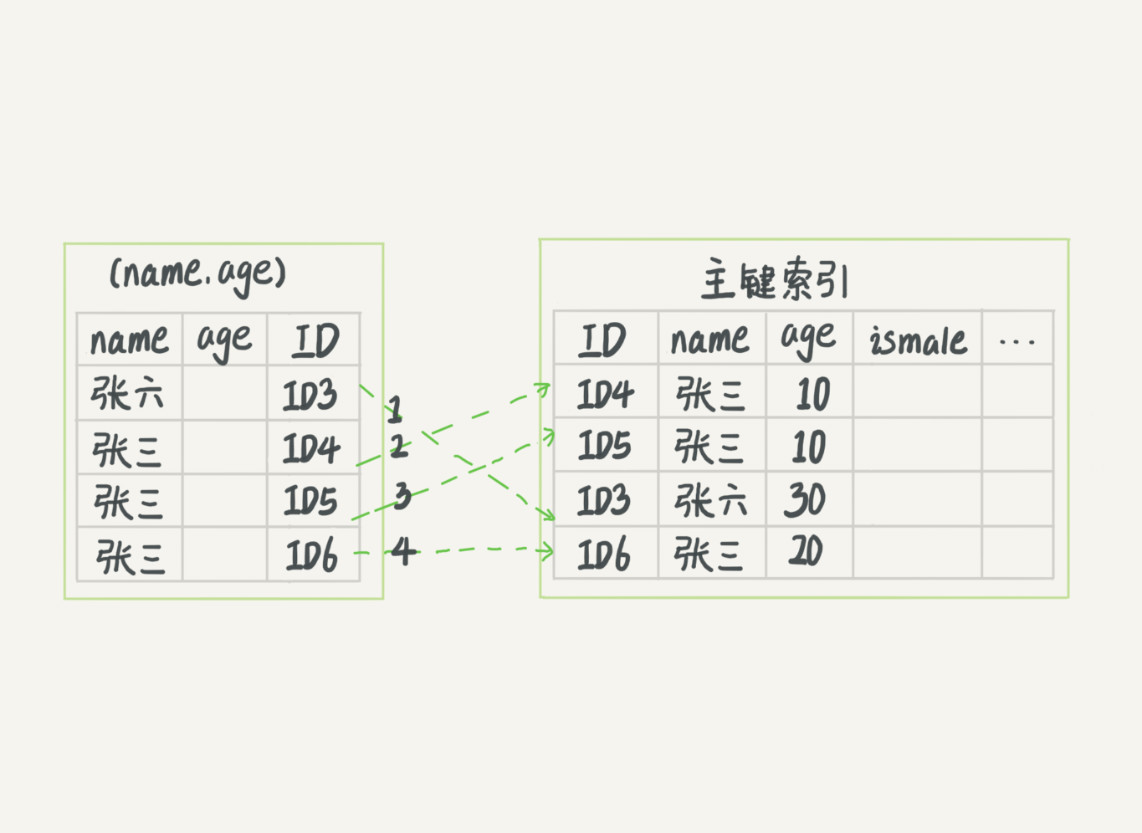
    • 如果查找所有名字为张三的人时，可以快速定位到ID4，然后向后遍历，直到不满足条件为止
    • 如果查找所有名字的第一个字是张的人，找到第一个符合条件的记录ID3，然后向后遍历，直到不满足条件为止

  2. 只要满足最左前缀，就可以利用索引来加速检索，最左前缀有2种情况

    • 联合索引的最左N个字段
    • 字符串索引的最左M个字符

  3. 建立联合索引时，定义索引内字段顺序的原则

    • 复用：如果通过调整顺序，可以少维护一个索引，往往优先考虑这样的顺序
    • 空间：维护(name,age)+age比维护(age,name)+name所占用的空间更少

索引下推

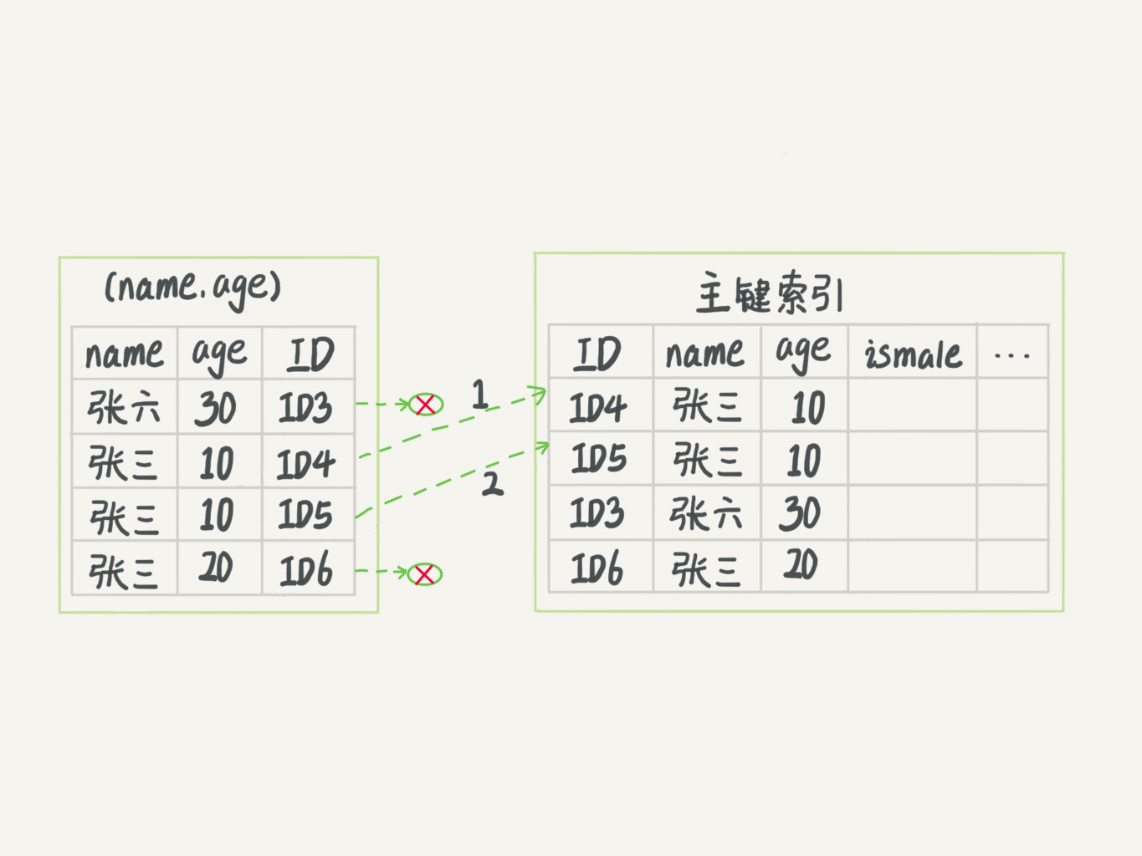
SELECT * FROM tuser WHERE name LIKE '张%' AND age=10 AND ismale=1;

  1. 依据最左前缀原则，上面的查询语句只能用张，找到第一个满足条件的记录ID3（优于全表扫描）

  2. 然后判断其他条件是否满足

    • 在MySQL 5.6之前，只能从ID3开始一个个回表，到聚簇索引上找出对应的数据行，再对比字段值
    • 这里暂时忽略MRR：在不影响排序结果的情况下，在取出主键后，回表之前，会对所有获取到的主键进行排序
    • 在MySQL 5.6引入了下推优化index condition pushdown）
    • 可以在索引遍历过程中，对索引所包含的字段先做判断，直接过滤掉不满足条件的记录，减少回表次数

无索引下推，回表4次
img

采用索引下推，回表2次
img

删除冗余索引

CREATE TABLE `geek` (
    `a` int(11) NOT NULL,
    `b` int(11) NOT NULL,
    `c` int(11) NOT NULL,
    `d` int(11) NOT NULL,
    PRIMARY KEY (`a`,`b`),
    KEY `c` (`c`),
    KEY `ca` (`c`,`a`),
    KEY `cb` (`c`,`b`)
) ENGINE=InnoDB;

# 索引(`a`,`b`)是业务属性
# 常规查询，应该如何优化索引？
select * from geek where c=N order by a limit 1;
select * from geek where c=N order by b limit 1;

结论

索引ca是不需要的，因为满足最左前缀原则，ca(b) = c(ab)

样例

假设表记录

a b c d
1 2 3 d
1 3 2 d
1 4 3 d
2 1 3 d
2 2 2 d
2 3 4 d

索引ca：先按c排序，再按a排序，同时记录主键

c a 部分主键b(只有b)
2 1 3
2 2 2
3 1 2
3 1 4
3 2 1
4 2 3

这与索引c是一样的，索引ca是多余的

参考资料

《MySQL实战45讲》

posted @ 2020-05-23 11:22  Yungyu  阅读(155)  评论(0)  编辑  收藏  举报