贝叶斯网络的

 联合概率表示两个事件共同发生的概率。A与B的联合概率表示为或者。

边缘概率（又称先验概率）是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization），比如A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。

 

 

 这是在任何情况下都成立的

再给出具体的贝叶斯网络图的情况下 可以化简  eg:

 

 

 

一个简单的贝叶斯网络:1+2+2+4+4:

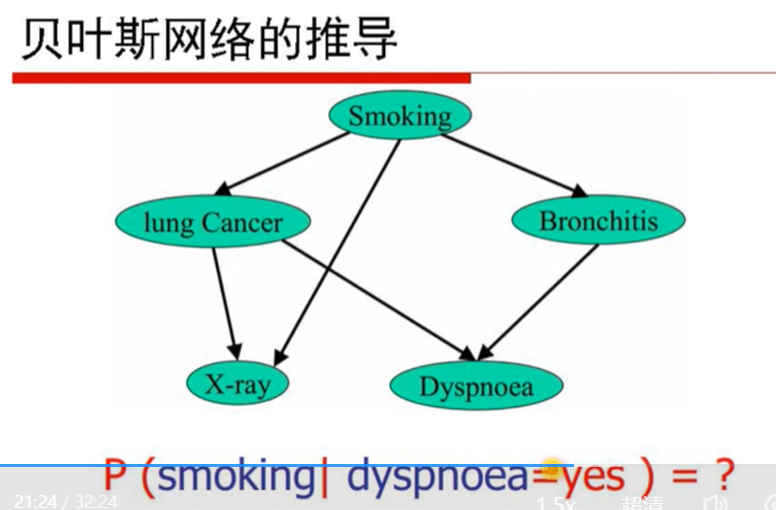
  1. 1是得到smoking概率需要的一个参数，吸烟或者不吸烟 已知吸烟为0.4 不吸就是0.6呗 所以知道一个就√

  2. 2是lung cancer的两个参数 他只和抽烟有关 抽烟的时候(患了肺癌/没患肺癌)是多少 不抽烟的时候(患了肺癌/没患肺癌)是多少 只需要两个参数最终会有四个数

  3. 4是呼吸困难的参数个数 ，肺癌又支气管炎的呼吸困难的概率xxxxxxxx00 01 10 11

那个 2*5

 

 

马尔可夫模型是个有向无环图，表示当前节点只和前一个结点有关的贝叶斯网络。 不同于马尔科夫网络

 

 

 

D分离

D-Separation方法可以快速的判断出DAG（有向无环图）两个节点之间是否是条件独立的

原理

对于给定的结点集ε，如果对贝叶斯网中的结点Vi和Vj(没说vij在Σ内)之间的每个无向路径，在路径上有某个结点Vb，如果有属性：

（1）Vb在ε中，且路径上的两条弧都以Vb为头（即弧在Vb处开始（出发））；

（2）Vb在ε中，路径上的一条弧以Vb为头，一条以Vb为尾 ；

（3）Vb和它的任何后继都不在ε中，路径上的两条弧都以Vb为头（即弧在Vb处结束）；

则称Vi和Vj 被Vb结点阻塞。

如果Vi和Vj被证据集合ε中的任意结点阻塞，则称Vi和Vj是被ε集合D分离，结点Vi和Vj条件独立于给定的证据集合ε，即P(Vi|Vj,ε) =P(Vi|ε)和P(Vj|Vi,ε) =P(Vj|ε)，表示为：I(Vi,Vj|ε) 或I(Vj,Vi|ε) 。

无向路径：DAG图是有向图，所以其中的路径也应该是有向路径，这里所指的无向路径是不考虑DAG图中的方向性时的路径。

条件独立：如具有以上三个属性之一，就说结点Vi和Vj条件独立于给定的结点集ε。

阻塞：给定证据集合ε，当上述条件中的任何一个满足时，就说Vb阻塞相应的那条路径。

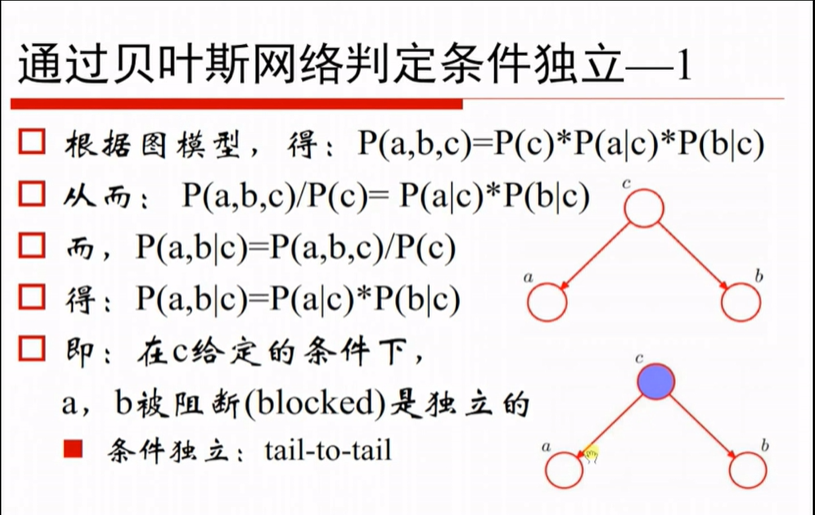
D分离：如果Vi和Vj之间所有的路径被阻塞，就叫证据集合ε可以D分离Vi和Vj。D分离的实质就是寻找贝叶斯网中的条件独立语义，以简化推理计算。

tail to tail

p(a,b,c) = p(c)p(a|c)p(b|c)

两边都/p(c)

又因为p(a b|c)ab的联合概率 = p(a,b,c)/p(c)

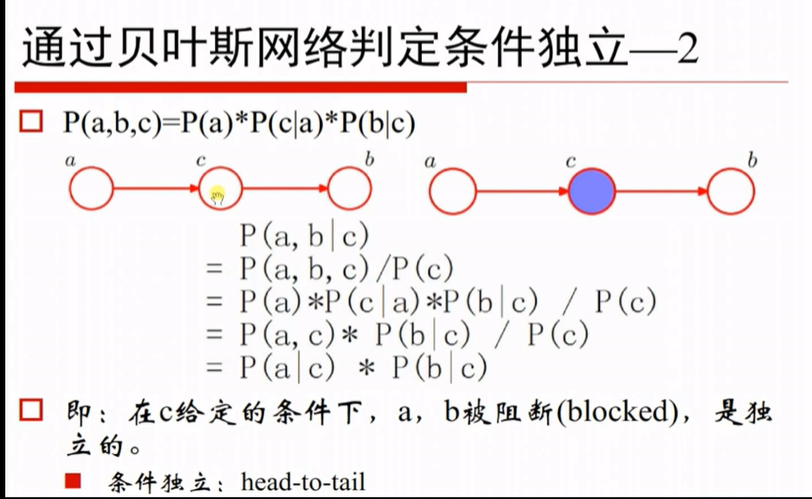
所以得p(a,b,c)/p(c) = p(a|c)p(b|c) 在c给定的条件下 p(a,b)=p(a)p(b) ab独立 即条件独立

 

head to tail

p(a,b,c) = p(a)p(c|a)p(b|c)

已知p(a,b|c) = p(a,b,c)/p(c) 带入p(a,b,c) = p(a)p(c|a)p(b|c)

又因为 p(a)p(c|a) = p(a,c)

就=p(a,c)p(b|c)/p(c) 就=p(a|c)p(b|c)=p(a,b|c) 在c给定得情况下 a b被阻断 是独立的

 

 

head to head

p(a,b,c) = p(a)p(b)p(c|a,b)

等号左右两侧给c做积分 得到p(a,b)=p(a)p(b) 即和c无关的情况下，ab独立

类似一个家庭 在没有孩子的时候 父母是独立的 有了孩子 父母双方就有联系了

 

 

 

 

 

原本联合公式 p(x1,x2,x3....) = p(xi|x1,x2,..xi-1)的  但是通过贝叶斯的具体情况 化简掉一些无关的变量

 

 

   

 

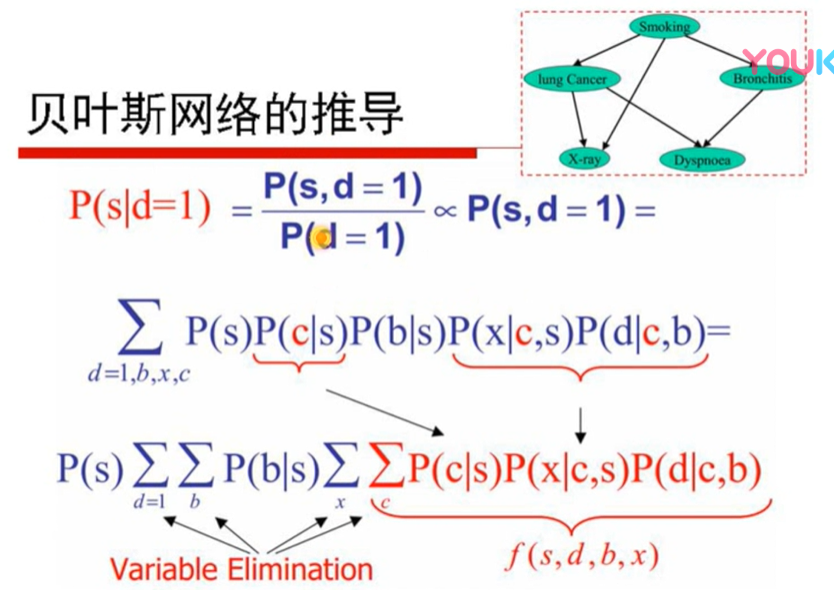
 p(d=1)是个规划因子，忽略，考虑联合分布，p(s|d=1) = p(s,c,b,x,d)的联合分布之后积掉bxc让d=1 就仍然相等 求出p(s|d)

 

 

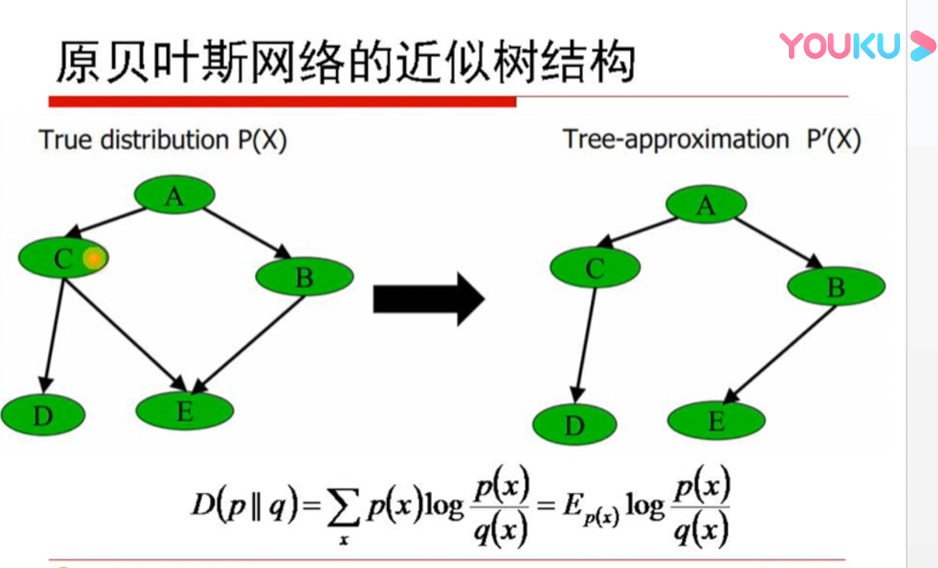
 想由p(x)变到p'(x) 取消环 让相对熵最小最接近 信息相关度最大

  

 

 以上内容来自  七月算法贝叶斯

 

伯努利分布、二项分布、Beta分布、多项分布和Dirichlet分布

伯努利试验 是只有两种可能结果的单次随机试验。

二项分布是重复多次的伯努利分布

典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率

多项分布:首先(如果在一次实验中，出现的结果不是2种而是k种可能 相对于伯努利)这样的实验进行n次(与二项分布 之于 伯努利分布 相同)

多项式分布（Multinomial Distribution）是二项式分布的推广。还是做n次试验，只不过每次试验的结果可以有多m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项式分布

狄利克雷分布（Dirichlet distribution）是Beta分布在高维情形的推广

Dirichlet分布可以看做是分布之上的分布。如何理解这句话，我们可以先举个例子：假设我们有一个骰子，其有六面，分别为{1,2,3,4,5,6}。现在我们做了10000次投掷的实验，得到的实验结果是六面分别出现了{2000,2000,2000,2000,1000,1000}次，如果用每一面出现的次数与试验总数的比值估计这个面出现的概率，则我们得到六面出现的概率，分别为{0.2,0.2,0.2,0.2,0.1,0.1}。现在，我们还不满足，我们想要做10000次试验，每次试验中我们都投掷骰子10000次。我们想知道，出现这样的情况使得我们认为，骰子六面出现概率为{0.2,0.2,0.2,0.2,0.1,0.1}的概率是多少（说不定下次试验统计得到的概率为{0.1, 0.1, 0.2, 0.2, 0.2, 0.2}这样了）。这样我们就在思考骰子六面出现概率分布这样的分布之上的分布。而这样一个分布就是Dirichlet分布。

β分布:

Beta分布可以看做是分布之上的分布。我们还是以抛硬币为例。不过，我们并不假设硬币是均匀的（也就是说：并不假设每次抛硬币，正面朝上的概率为0.5），所以抛硬币的正面朝上的概率p是未知的（只知道p∈[0,1]）。如果进行一次二项分布试验，在这次二项分布试验中，抛硬币10000次，其中正面朝上7000次，反面朝上3000次，我们可以得到，正负面朝上的概率分别为{p,1-p}={0.7,0.3}。但是我们并不确信这个结果是正确的。我们想要做10000次二项分布试验，在每次二项分布试验中，均抛硬币10000次（说不定在其他二项分布实验中，得到的正负面朝上的概率是{0.2,0.8}或者{0.6,0.4}，这些情况都有可能），那么，我们想要知道，在这样的多次重复二项分布实验中，抛硬币最后得到正负面朝上概率为{0.7,0.3}这样概率为多少？这就是在求抛硬币的概率分布之上的分布。这样的分布就叫做Beta分布。

正如二项分布可以看做多次进行伯努利试验所得到的分布一样，Beta分布也可以看做是多次进行二项分布的试验所得到的分布，是分布之上的分布。

 大家讲解的大都内容不全 有点怪怪的 信息还是少

 

 

Long Long Ago

 概率派：认为打中靶子的概率是就是0.7(固定的)，打了一枪中/没中的概率是随机的 中没中画一个分布表

需要推断的参数θ看做是固定的未知常数，即概率img虽然是未知的，但最起码是确定的一个值，同时，样本X 是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本X 的分布；

最大似然估计(MLE)和最大后验估计(MAP)都是把待估计的参数看作一个拥有固定值的变量，只是取值未知。通常估计的方法都是找使得相应的函数最大时的参数；

贝叶斯派：往桌子上扔球，球掉在某个地方的概率是随机的，球掉在这个位置那个位置的概率 我知道他要是掉在某个地方，概率是多少，但我不确定他掉在哪

一个朋友创业，你明明知道创业的结果就两种，即要么成功要么失败，但你依然会忍不住去估计他创业成功的几率有多大？你如果对他为人比较了解，而且有方法、思路清晰、有毅力、且能团结周围的人，你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式，便是贝叶斯式的思考方式。

 最大似然估计

  1. 也称为极大似然估计 https://www.bilibili.com/video/av15944258/ 模型已定，参数未知 利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。 最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。 https://blog.csdn.net/zengxiantao1994/article/details/72787849

贝叶斯估计

频率学派的代表是最大似然估计(MIE)；贝叶斯学派的代表是最大后验概率估计(MAP)

两大学派的争论             频率学派与贝叶斯学派只是解决问题的角度不同。

在对事物建模时，用θ表示模型的参数，请注意，解决问题的本质就是求θ。那么：

(1) 频率学派：存在唯一真值θ。举一个简单直观的例子—抛硬币，我们用P(head)来表示硬币的bias。抛一枚硬币100次，有20次正面朝上，要估计抛硬币正面朝上的bias P(head)=θ。在频率学派来看，θ= 20 / 100 = 0.2，很直观。

当数据量趋于无穷时，这种方法能给出精准的估计；然而缺乏数据时则可能产生严重的偏差。例如，对于一枚均匀硬币，即θ= 0.5，抛掷5次，出现5次正面 (这种情况出现的概率是1/2^5=3.125%)，频率学派会直接估计这枚硬币θ= 1，出现严重错误。

(2) 贝叶斯学派： θ是一个随机变量，符合一定的概率分布。在贝叶斯学派里有两大输入和一大输出，输入是先验 (prior)和似然 (likelihood)，输出是后验 (posterior)。

同样是抛硬币的例子，对一枚均匀硬币抛5次得到5次正面，如果先验认为大概率下这个硬币是均匀的 (例如最大值取在0.5处的Beta分布)，那么P(head)，即P(θ|X)，是一个distribution，最大值会介于0.5~1之间，而不是武断的θ= 1。

你可能会问：如果连数据都没有，我怎么知道我的参数是怎么分布的？你提出这个问题，就说明你是一个赤裸裸的频率派学家，你需要通过数据来得到你的参数！而这并不是贝叶斯派的考虑，贝叶斯估计最重要的就是那个先验的获得。虽然你这次的一组数据，比如说扔三次硬币产生的序列是（110）这样分布的，但是其实我根据我历史的经验来看，一枚硬币正反面其实很有可能是按照均匀分布来的，只不过可能因为你抛得次数少了所以产生了不是均匀分布的效果。所以我要考虑我以往的经验在里面。

你可能又会问：那你这个均匀分布不就是完全猜来的嘛，你怎么知道我这次是不是一样的硬币呢？没错！就是“猜来的”。先验在很多时候完全是假设，然后去验证有的数据是否吻合先验猜想，所以这里的猜很重要。还要注意，先验一定是与数据无关的，你不能看到了数据再做这些猜想，一定是没有任何数据之前你就猜了一个参数的先验概率。 率表示为P(A|B)，读作“在B条件下A的概率”。

 

如果一枚硬币抛10次，10次均为正面，根据最大似然估计，那么这枚硬币的概率应该为1。

当抛硬币10次，10次都是正面的时候，最大后验估计 [公式] 是一个分布，最大值位于0.5~1之间，哪怕是抛硬币100次，100次都是正面的时候，最大后验估计 [公式] 的最大值接近1，但依然不是1

极大似然估计是想让似然函数极大化，而考虑了MAP算法的贝叶斯估计，其实是想让后验概率极大化。主要区别在于估计参数中，一个考虑了先验一个没有考虑先验

 

贝叶斯定理

贝叶斯定理是关于随机事件A和B的条件概率和边缘概率的一则定理。

img

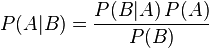
P(B)=P(B|A)P(A)+P(B|∼A)P(∼A)

在参数估计中可以写成下面这样：

img

这个公式也称为逆概率公式，可以将后验概率转化为基于似然函数和先验概率的计算表达式，即

img

在贝叶斯定理中，每个名词都有约定俗成的名称：

P(A)是A的先验概率先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。 P(A|B)是已知B发生后A的条件概率(在B发生的情况下A发生的可能性)，也由于得自B的取值而被称作A的后验概率。 P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。 P(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）. 按这些术语，Bayes定理可表述为：

后验概率 = (相似度*先验概率)/标准化常量，也就是说，后验概率与先验概率和相似度的乘积成正比。 另外，比例P(B|A)/P(B)也有时被称作标准相似度（standardised likelihood），Bayes定理可表述为：

后验概率 = 标准相似度*先验概率

 

共轭先验

在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验。

似然函数

似然（likelihood）这个词其实和概率（probability）是差不多的意思，Colins字典这么解释：The likelihood of something happening is how likely it is to happen. 你把likelihood换成probability，这解释也读得通。但是在统计里面，似然函数和概率函数却是两个不同的概念（其实也很相近就是了）。

对于这个函数：

P(x|θ) 输入有两个：x表示某一个具体的数据；θθ表示模型的参数。

如果θθ是已知确定的，xx是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。

如果xx是已知确定的，θθ是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。

 

 

 

贝叶斯网络结构学习

    1. 基于评分搜索的方法

      那么如何根据已有的数据集学得贝叶斯网络结构呢？一种最简单的想法就是遍历所有可能的结构，然后用某个标准去衡量各个结构，进而找出最好的结构。

      是的，这就是评分搜索的基本思想

      其中，评分函数和搜索策略是主要因素

      1.常用的评分函数

      1. 基于贝叶斯统计的评分函数

        1. P(G|D)=P(D|G)P(G)/P(D)通常分母是连续的，与拓扑结构G无关，因此应该最大化分子P(D|G)P(G)，因此其核心思想就是给定训练数据集D，寻求具有最大后验概率的拓扑结构。因此两边取对数log(P(S|D)) = log(P(D/G))+log(P(S))

        2. K2评分函数 BIC BD评分 BDe评分函数

      2. 基于信息理论的评分函数

        1. 主要理论是最小描述长度原理MDL，基于MDL的评分函数具有2个部分，训练数据集的似然函数值Ldata和网络模型的复杂度Lnet,MDL的测度表示为Ldata-Lnet

      2.搜索策略：贪心搜索,爬山法，模拟退火，

    2. 基于条件独立测试的方法

      经过Drafting,Thickening,Thinning三个步骤,通过计算相互信息量(Mutual Information)来确定结点间的条件独立

    3.  

 

 

posted @ 2019-09-30 21:07  像走了一光年  阅读(1057)  评论(0)  编辑  收藏  举报