数据描述性统计度量方法
数据描述性统计度量主要包括:集中趋势和离散趋势
1、集中趋势
集中趋势的度量主要包括:均值、众数、中位数

均值扩展:
(1) 带权平均值:
权重反应的是样本在总体样本中的意义、重要性或出现的频率。
带权平均值主要用于应对不同样本的权重不一样。

(2) 截尾平均值:
截尾均值是指丢弃极端样本值后的均值。主要用于抵消少数极端值的影响。
应对于不同的数据类型时,均值、中位数和众数所能表示的集中趋势度量可靠性不同: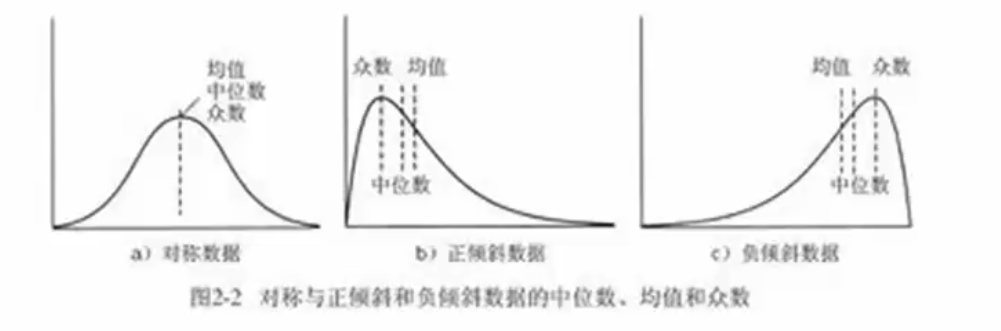
小技巧:对于适度倾斜(非对称)的单峰数值数据,平均数减众数约等于三倍的平均数减中位数。
2、离散趋势
离散趋势的度量主要包括:极差、方差、标准差
方差计算简化公式:
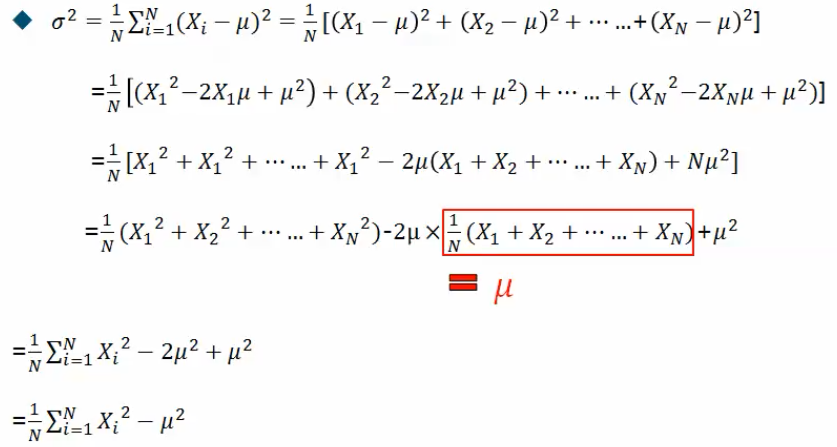
标准差的意义:为弥补方差数值与样本的单位不同而造成的无法准确表示相差数值的遗憾,如,当样本单位为m时,方差数值的单位为m2,而标准差与样本单位相同。
3、常用来直观描述数据的图形
数据通常不能直观的被人所感知,通过将数据可视化为图形时,可使人更容易理解和察觉数据隐含的意义。
常用统计图对比:

(1) 直方图
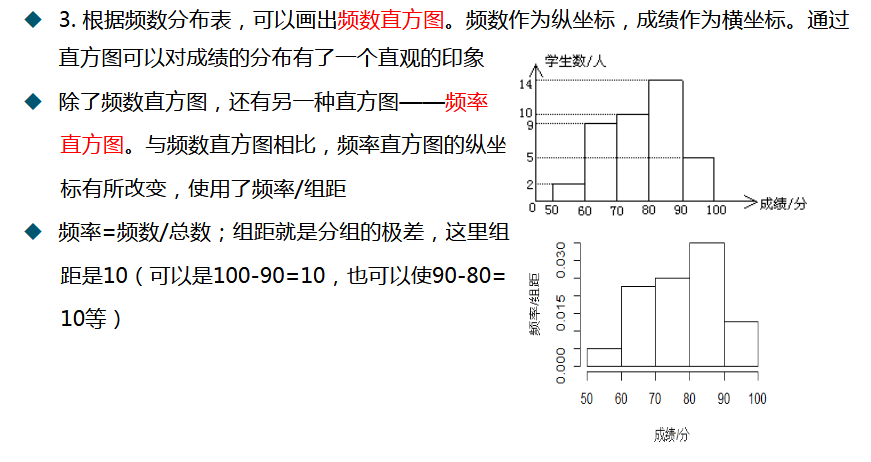
(2) 箱线图
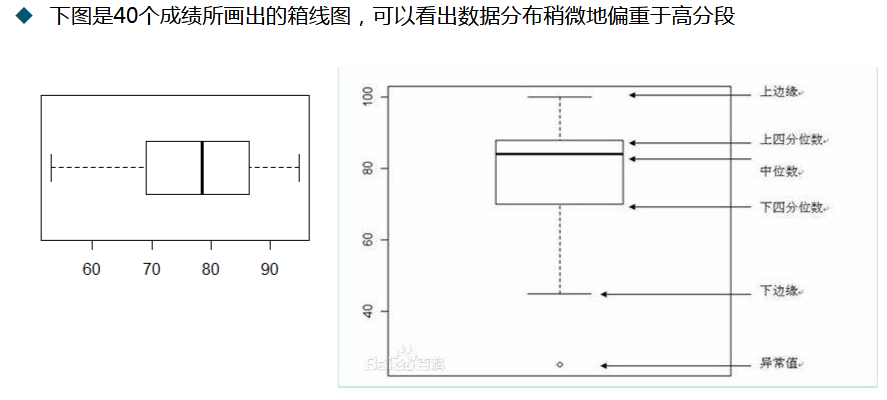

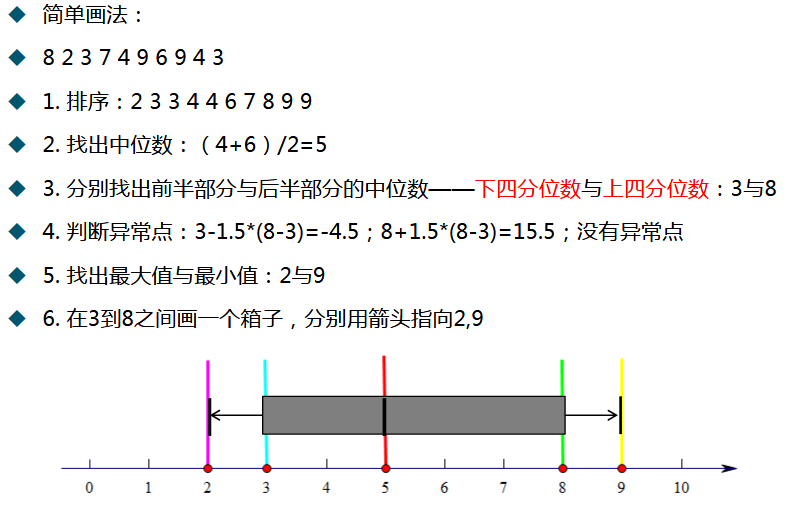
(3) 茎叶图
茎叶图可以在保留全部数据信息的情况下,直观地显示出数据的分布情冴

(4) 线图
线图即为曲线图和折线图
(5) 柱形图(条形图)
显示一段时间内的数据变化或者显示各项数据在同一情况下的比较情况
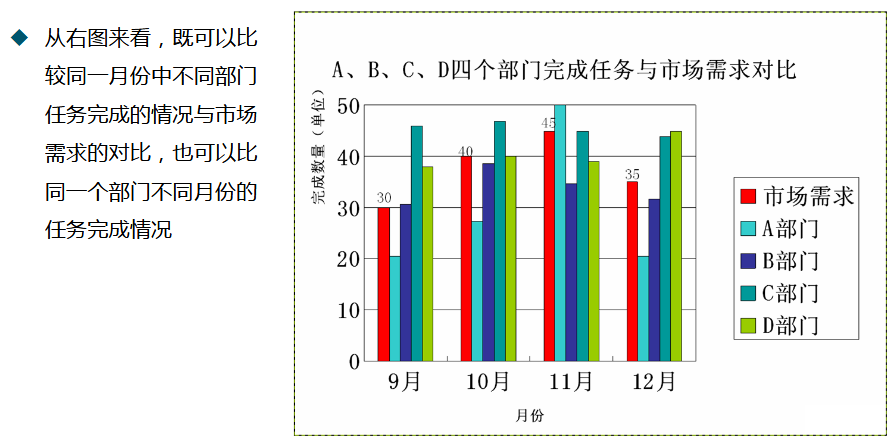
柱形图与直方图的对比:
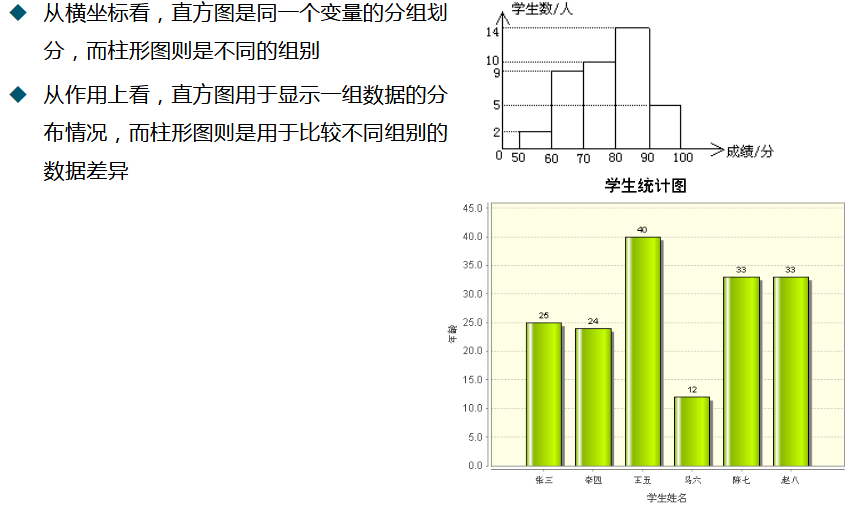
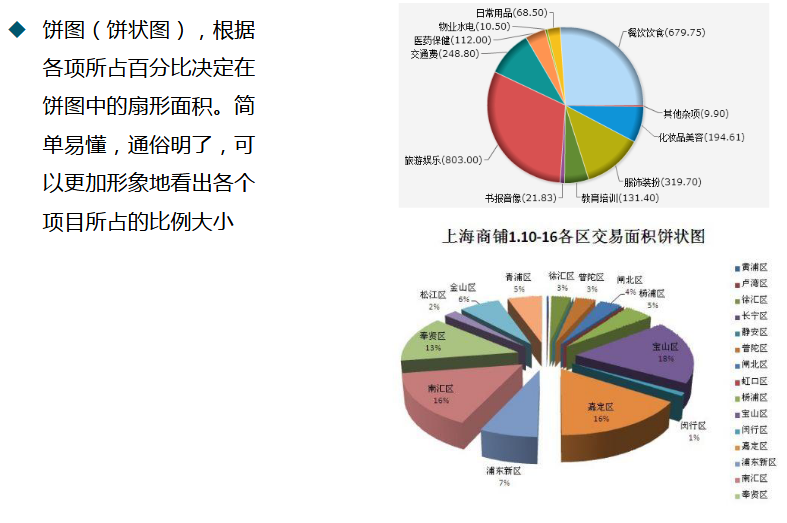
(5) 饼图
显示一段时间内的数据变化或者显示各项数据在同一情况下的比较情况