第二章：数组结构

2.1 线性表简介

1 线性表：

　　1）有序表可以是空集合，或者写成（a₁，a₂，a₃，......，a_n，a_n）

　　2）存在唯一的第一个元素a₁和唯一最后一个元素a_n。

　　3）除了第一个元素a₁ 外，每一个元素都有唯一的先行者。

　　4）除了最后一个元素a_n 外，每一个元素都有唯一的后继者。

2 线性表存储结构：

　　静态数据结构：也称为“密集表”，它使用连续分配的内存空间来存储有序表中的数据。（静态数据结构是在编译时就给相关的变量分配好内存空间。在建立静态数据结构的初期，必须声明最大可能要占用的固定内存空间，因此容易造成内存浪费。优点：设计简单，读取与修改表中任意元素的时间是固定的。缺点：删除或加入数据时，需要移动大量数据）

　　动态数据结构：也称为“链表”，它使用不连续的内存空间存储具有线性表特性的数据。（优点：数据的插入或删除都相当方便，不需要移动大量数据。内存是在程序执行时才进行分配，所以不需要事先声明，节省内存。缺点：设计数据结构麻烦，查找数据时，无法像静态数据一般可以随机读取，必须直到按顺序找到改数据为止）

2.2 认识数组

1 数组类型的声明：

　　1）起始地址：表示数组名（或数组第一个元素）所在内存中的起始地址。

　　2）维度：一维、二维、三维。

　　3）索引上下限：

　　4）数组元素个数：是索引上限和索引下限的差加1。

　　5）数组类型：声明此数组的类型，它决定数组元素在内存所占容量的大小。

　　程序1是记录5个人分数，然后求平均值。

# 记录5个人分数，然后求平均
#一维列表使用
Score = [87,66,90,65,70]
Total_Score = 0
for count in range(5):
    print('第 %d 位学生的分数：%d' %(count+1,Score[count]))
    Total_Score += Score[count]
print('--------------------------')
print('5位学生的总分：%d' %Total_Score)

　　程序2表示的是输入一个二维列表表示的二阶行列式，并计算结果。

N = 2
# 声明二维数组
arr = [ [None]*N for row in range(N) ]
print('|a1  b1|')
print('|a2  a2|')
arr[0][0] = input('请输入a1：')
arr[0][1] = input('请输入b1：')
arr[1][0] = input('请输入a2：')
arr[1][1] = input('请输入b2：')
#求第二阶行列式的值
result = int(arr[0][0]) * int(arr[1][1]) - int(arr[0][1])*int(arr[1][0])
print('|%d  %d|'    %(int(arr[0][0]),int(arr[0][1])))
print('|%d  %d|'    %(int(arr[1][0]),int(arr[1][1])))
print('行列式值=%d' %result)

　　程序3表示的找出2 X 3 X 3 三维数组中存储数值的最小值。

# 三维数组
num = [ [ [33,45,67],[23,71,66],[55,38,66] ],\
       [ [21,9,15],[38,69,18],[90,101,89] ] ]
value = num[0][0][0]
print(num)
for i in range(2):
    for j in range(3):
        for k in range(3):
            if(value>=num[i][j][k]):
                value = num[i][j][k]
print("最小值= %d" %value)

 

2.3 矩阵

矩阵作为一种常用的数据结构，在数据计算中比较常用。此节主要讨论两个矩阵的相加、相乘，以及某些稀疏矩阵、转置矩阵、上三角矩阵和下三角矩阵等。

1 矩阵相加

　　矩阵的相加比较简单，只要求两矩阵对应的行数和列数都相等，相加后的矩阵也同样行列数矩阵。

　　程序4列出两个矩阵的相加及结果的程序。

#声明两个数组来实现两个矩阵的相加
A = [[1,3,5],[7,9,11],[13,15,17]] #二维数组的声明
B = [[9,8,7],[6,5,4],[3,2,1]]
N = 3
C = [ [None] * N for row in range(N) ]

for i in range(3):
    for j in range(3):
        C[i][j] = A[i][j] + B[i][j] #矩阵相加
print('矩阵A和矩阵B相加的结果：')
for i in range(3):
    for j in range(3):
        print('%d' %C[i][j],    end='\t')
    print('\n')

2 矩阵相乘

　　矩阵相乘有一些限制，两个矩阵A和B相乘，必须是A矩阵的列和B矩阵的行相同。例如：A：m X n，B：n X p ,则A X B = m X p矩阵。

　　程序5表示的是设计程序实现两个可自行输入矩阵维数的矩阵相乘过程，并显示结果。

# 可以实现两个自行输入矩阵维度的矩阵相乘，并输出结果
def MatrixMultiply(arrA,arrB,arrC,M,N,P):
    global C
    if M<=0 or N<=0 or P<=0:
        print('[错误：维数M,N,P必须大于0]')
        return
    for i in range(M):
        for j in range(P):
            Temp = 0
            for k in range(N):
                Temp = Temp + int(arrA[i*N+k])*int(arrB[k*P+j])
            arrC[i*P+j] = Temp

print('请输入矩阵A的维数（M,N）：')
M = int(input('M= '))
N = int(input('N= '))
A = [None]*M*N  #声明大小为M*N的列表A

print('请输入矩阵A的各个元素：')
for i in range(M):
    for j in range(N):
        A[i*N+j]=input('a%d%d=' %(i,j))

print('请输入矩阵B的维数（N,P）：')
N = int(input('N= '))
P = int(input('P= '))

B = [None]*N*P #声明N*P的列表B

print('[请输入矩阵B的各个元素]')
for i in range(N):
    for j in range(P):
        B[i*P+j] = input('b%d%d=' %(i,j))


C = [None]*M*P #声明大小为M*P的列表C
MatrixMultiply(A,B,C,M,N,P) # 函数调用
print('A X B 的结果是：')
for i in range(M):
    for j in range(P):
        print('%d' %C[i*P+j],end='\t')
    print('\n')

　　针对上述的程序，重点在于定义的相乘函数。

def MatrixMultiply(arrA,arrB,arrC,M,N,P):
    global C
    if M<=0 or N<=0 or P<=0:
        print('[错误：维数M,N,P必须大于0]')
        return
    for i in range(M):
        for j in range(P):
            Temp = 0
            for k in range(N):
                Temp = Temp + int(arrA[i*N+k])*int(arrB[k*P+j])
            arrC[i*P+j] = Temp

3 矩阵转置

　　转置矩阵就是把原矩阵的行坐标和列坐标元素相互调换。

　　程序6展示的是一个4*4二维数组的转置。

# 4 X 4 二维数组的转置

arrA = [ [1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16] ]
N = 4
#声明4 X 4 数组arr
arrB = [ [None]*N for row in range(N) ]

print('原设置的矩阵内容：')
for i in range(4):
    for j in range(4):
        print('%d' %arrA[i][j],end='\t')
    print(' ')

# 进行矩阵的转置操作
for i in range(4):
    for j in range(4):
        arrB[i][j]=arrA[j][i]

print('转置矩阵的内容为：')
for i in range(4):
    for j in range(4):
        print('%d' %arrB[i][j],end='\t')
    print(' ')

4 稀疏矩阵

　　定义：如果一个矩阵中的大部分元素为零，就被称为稀疏矩阵。

　　缺点：如果一个矩阵里面0元素过于多，存储就特别占内存空间，于是需要提高效率使用三项式的数据结构。

　　假如一个稀疏矩阵有n个非零项，那么可以利用一个A（0：n，1:3）二维数组来存储这些非零项，称之为矩阵的压缩矩阵。

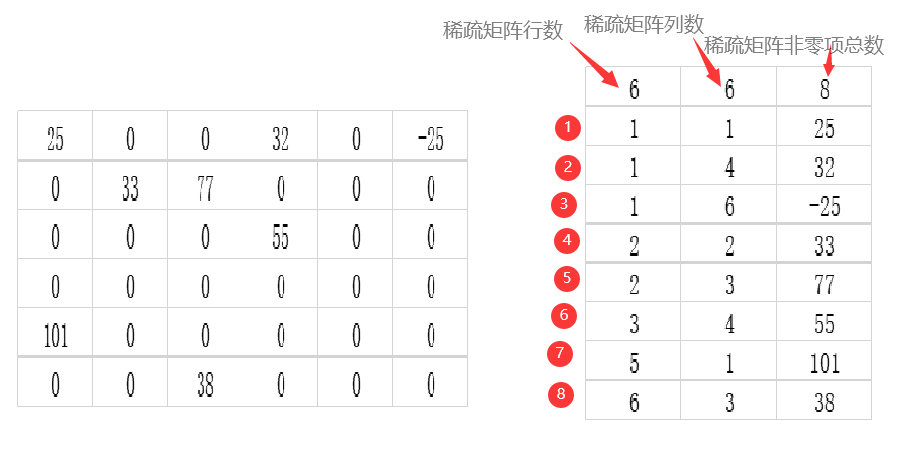
　　程序7展示的是一个6*6的稀疏矩阵压缩过程及结果。

# 设计一个python程序利用三项式数据结构，并压缩6*6稀疏矩阵，以减少内存不必要的浪费
NONZERO = 0
temp = 1
Sparse = [ [25,0,0,22,0,-15],[0,11,3,0,0,0],
           [0,0,0,-6,0,0],[0,0,0,0,0,0],
           [91,0,0,0,0,0],[0,0,28,0,0,0] ]
Compress = [ [None]*3 for row in range (9) ] #声明压缩矩阵

print('稀疏矩阵的各元素个数') #打印系数矩阵的各个元素
for i in range(6):
    for j in range(6):
        print('[%d]'    %Sparse[i][j],end=' ')
        if Sparse[i][j] != 0:
            NONZERO = NONZERO +1
    print(' ')

# 开始压缩稀疏矩阵
Compress[0][0]=6
Compress[0][1]=6
Compress[0][2]=NONZERO

for i in range(6):
    for j in range(6):
        if Sparse [i][j] != 0:
            Compress[temp][0]=i
            Compress[temp][1]=j
            Compress[temp][2]=Sparse[i][j]
            temp = temp + 1

print('稀疏矩阵压缩后的内容')
for i in range(NONZERO+1):
    for j in range(3):
        print('[%d]'    %Compress[i][j],end=' ')
    print(' ')

5 上三角形矩阵

　　

6 

 

2.4 数组与多项式

 

---

 

后记：

1）详细补充随后附上

2）思考一下，总结一下。