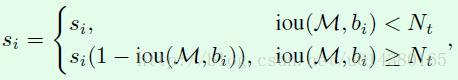Soft NMS算法笔记
Soft NMS算法笔记
论文：Improving Object DetectionWith One Line of Code
论文链接：https://arxiv.org/abs/1704.04503
这篇ICCV2017的文章，是NMS算法的改进，从论文题目可以看出，改进仅仅花了一行代码！首先NMS（Non maximum suppression）是在object detection算法中必备的后处理步骤，目的是用来去除重复框，也就是降低误检（false positives）。NMS算法的大致过程可以看原文这段话：First, it sorts all detection boxes on the basis of their scores. The detection box M with the maximum score is selected and all other detection boxes with a significant overlap (using a pre-defined threshold) with M are suppressed. This process is recursively applied on the remaining boxes.
那么传统的NMS算法存在什么问题呢？可以看Figure1。在Fiugre1中，检测算法本来应该输出两个框，但是传统的NMS算法可能会把score较低的绿框过滤掉（如果绿框和红框的IOU大于设定的阈值就会被过滤掉），导致只检测出一个object（一个马），显然这样object的recall就比较低了。
可以看出NMS算法是略显粗暴（hard），因为NMS直接将和得分最大的box的IOU大于某个阈值的box的得分置零，那么有没有soft一点的方法呢？这就是本文提出Soft NMS。那么Soft-NMS算法到底是什么样呢？简单讲就是：An algorithm which decays the detection scores of all other objects as a continuous function of their overlap with M. 换句话说就是用稍低一点的分数来代替原有的分数，而不是直接置零。另外由于Soft NMS可以很方便地引入到object detection算法中，不需要重新训练原有的模型，因此这是该算法的一大优点。
Figure2是Soft NMS算法的伪代码。首先是关于三个输入B、S、Nt，在FIgure2中已经介绍很清楚了。D集合用来放最终的box，在boxes集合B非空的前提下，搜索score集合S中数值最大的数，假设其下标为m，那么bm（也是M）就是对应的box。然后将M和D集合合并，并从B集合中去除M。再循环集合B中的每个box，这个时候就有差别了，如果是传统的NMS操作，那么当B中的box bi和M的IOU值大于阈值Nt，那么就从B和S中去除该box；如果是Soft NMS，则对于B中的box bi也是先计算其和M的IOU，然后该IOU值作为函数f()的输入，最后和box bi的score si相乘作为最后该box bi的score。就是这么简单！
接下来得重点就是如何确定函数f()了。
首先NMS算法可以用下面的式子表示：
为了改变NMS这种hard threshold做法，并遵循iou越大，得分越低的原则（iou越大，越有可能是false positive），自然而然想到可以用下面这个公式来表示Soft NMS：
但是上面这个公式是不连续的，这样会导致box集合中的score出现断层，因此就有了下面这个Soft NMS式子（也是大部分实验中采用的式子）：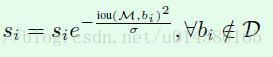 
这个式子满足了：A continuous penalty function should have no penalty when there is no overlap and very high penalty at a high overlap.
实验结果：
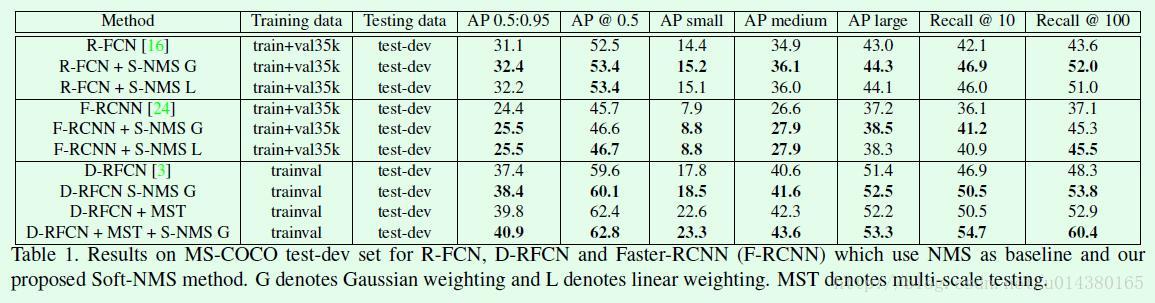
Table1是在MS-COCO数据集上的结果对比。表中的G表示上面连续的Soft NMS公式，L表示上面不连续的Soft NMS公式，从实验对比可以看出二者之间的差别并不大。对于G类型的Soft NMS，参数a取0.5，对于L类型的Soft NMS，参数Nt取0.3（感觉这个参数取的有点偏低）。
Table2是在VOC 2007数据集上的结果对比。
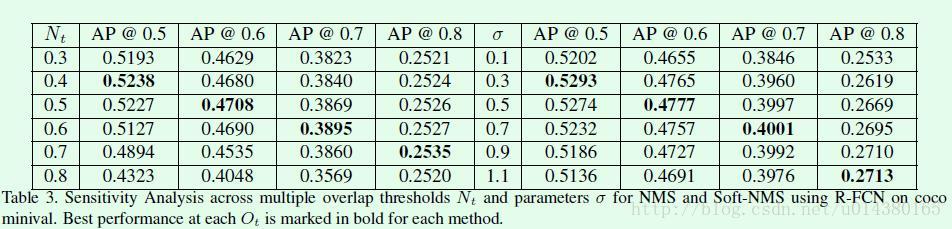
Table3是一个很不错的对比图。左边一半是NMS，右边一半是Soft NMS。在NMS部分，相同Ot条件下（Ot较小的情况下），基本上Nt值越大，其AP值越小，这主要是因为有越多的重复框没有过滤掉。
