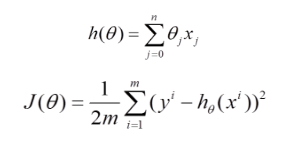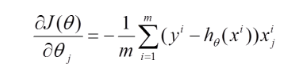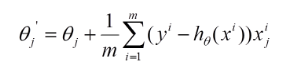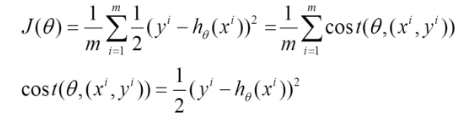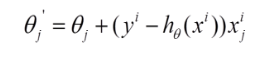最优化问题综述

最优化问题综述

 

1 优化问题分类

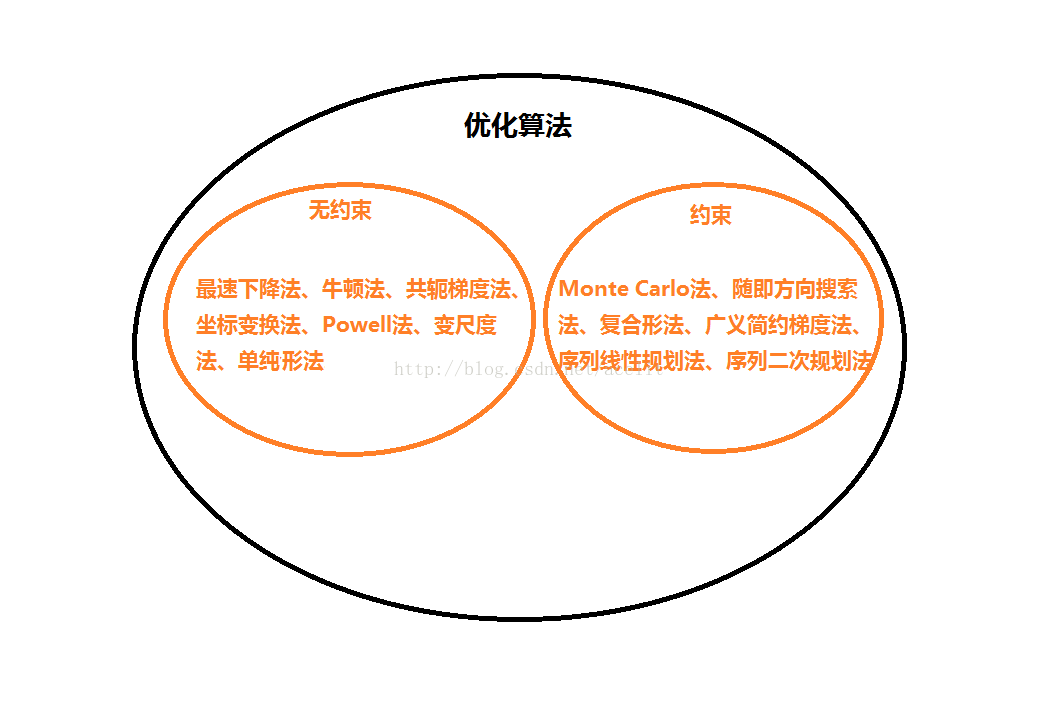
优化问题一般可分为两大类：无约束优化问题和约束优化问题，约束优化问题又可分为含等式约束优化问题和含不等式约束优化问题。

 

  • 无约束优化问题
  • 含等式约束的优化问题
  • 含不等式约束的优化问题

 

 

2 求解策略

针对以上三种情形，各有不同的处理策略：

 

  • 无约束的优化问题：可直接对其求导，并使其为0，这样便能得到最终的最优解；
  • 含等式约束的优化问题：主要通过拉格朗日乘数法将含等式约束的优化问题转换成为无约束优化问题求解；
  • 含有不等式约束的优化问题：主要通过KKT条件(Karush-Kuhn-Tucker Condition)将其转化成无约束优化问题求解。

 

3 求解算法

3.1 无约束优化算法

ref:http://www.cnblogs.com/maybe2030/p/4751804.html

3.1.1 梯度下降法

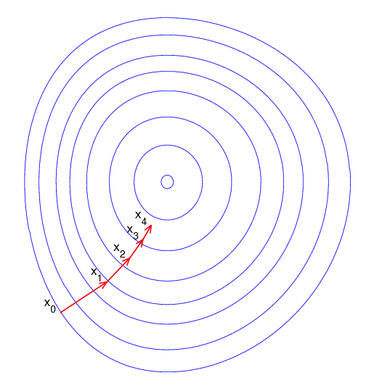
梯度下降法是最早最简单，也是最为常用的最优化方法。梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近目标值，步长越小，前进越慢。梯度下降法的搜索迭代示意图如下图所示：

　　牛顿法的缺点：

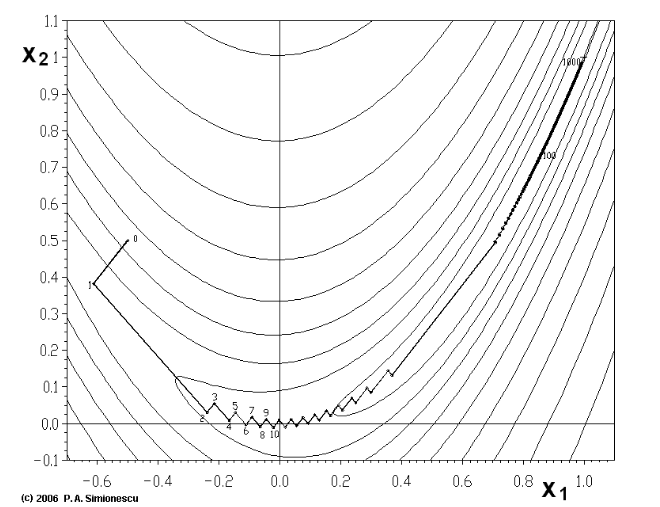
　　（1）靠近极小值时收敛速度减慢，如下图所示；

　　（2）直线搜索时可能会产生一些问题；

　　（3）可能会“之字形”地下降。

　　从上图可以看出，梯度下降法在接近最优解的区域收敛速度明显变慢，利用梯度下降法求解需要很多次的迭代。

　　在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。

　　比如对一个线性回归（Linear Logistics）模型，假设下面的h(x)是要拟合的函数，J(theta)为损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的样本个数，n是特征的个数。

 

 

　　1）批量梯度下降法（BatchGradient Descent，BGD）

　　（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度：

 

　　（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta：

 

　　（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度会相当的慢。所以，这就引入了另外一种方法——随机梯度下降。

　　对于批量梯度下降法，样本个数m，x为n维向量，一次迭代需要把m个样本全部带入计算，迭代一次计算量为m*n2。

　　2）随机梯度下降（StochasticGradient Descent，SGD）

　　（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

　　（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta：

 

　　（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

　　随机梯度下降每次迭代只使用一个样本，迭代一次计算量为n2，当样本个数m很大的时候，随机梯度下降迭代一次的速度要远高于批量梯度下降方法。两者的关系可以这样理解：随机梯度下降方法以损失很小的一部分精确度和增加一定数量的迭代次数为代价，换取了总体的优化效率的提升。增加的迭代次数远远小于样本的数量。

　　对批量梯度下降法和随机梯度下降法的总结：

　　批量梯度下降---最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小，但是对于大规模样本问题效率低下。

随机梯度下降---最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近，适用于大规模训练样本情况。

3.1.2 牛顿法和拟牛顿法

　1）牛顿法（Newton's method）

　　牛顿法是一种在实数域和复数域上近似求解方程的方法。方法是用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。

　　具体步骤：

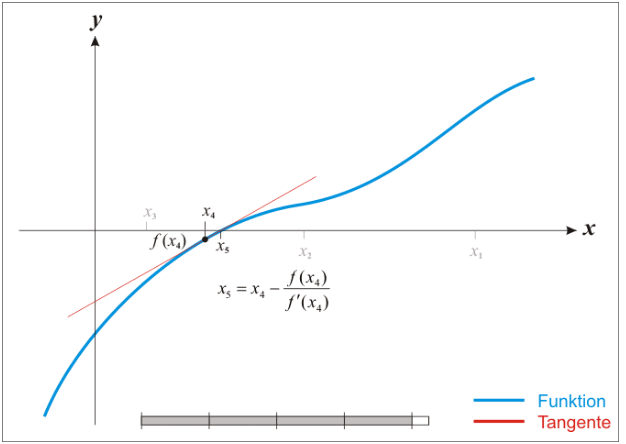
　　首先，选择一个接近函数 f (x)零点的 x0，计算相应的 f (x0) 和切线斜率f  ' (x0)（这里f ' 表示函数 f  的导数）。然后我们计算穿过点(x0,  f  (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标，也就是求如下方程的解：

　　我们将新求得的点的 x 坐标命名为x1，通常x1会比x0更接近方程f  (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示：

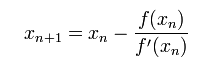
　　已经证明，如果f  ' 是连续的，并且待求的零点x是孤立的，那么在零点x周围存在一个区域，只要初始值x0位于这个邻近区域内，那么牛顿法必定收敛。 并且，如果f  ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。

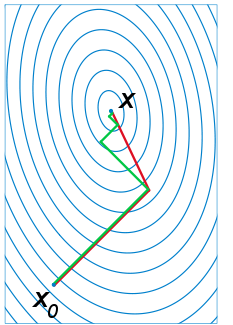
由于牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是"切线法"。牛顿法的搜索路径（二维情况）如下图所示：

　　牛顿法搜索示例图：

 

　　关于牛顿法和梯度下降法的效率对比：

　　从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

　　根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

注：红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。

　　牛顿法的优缺点总结：

　　优点：二阶收敛，收敛速度快；

　　缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。

　　2）拟牛顿法（Quasi-Newton Methods）

　　拟牛顿法是求解非线性优化问题最有效的方法之一，于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。Davidon设计的这种算法在当时看来是非线性优化领域最具创造性的发明之一。不久R. Fletcher和M. J. D. Powell证实了这种新的算法远比其他方法快速和可靠，使得非线性优化这门学科在一夜之间突飞猛进。

　　拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化，构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法，尤其对于困难的问题。另外，因为拟牛顿法不需要二阶导数的信息，所以有时比牛顿法更为有效。如今，优化软件中包含了大量的拟牛顿算法用来解决无约束，约束，和大规模的优化问题。

　　具体步骤：

　　拟牛顿法的基本思想如下。首先构造目标函数在当前迭代xk的二次模型：

　　这里Bk是一个对称正定矩阵，于是我们取这个二次模型的最优解作为搜索方向，并且得到新的迭代点：
　　其中我们要求步长ak  
满足Wolfe条件。这样的迭代与牛顿法类似，区别就在于用近似的Hesse矩阵Bk  
代替真实的Hesse矩阵。所以拟牛顿法最关键的地方就是每一步迭代中矩阵Bk
  
 
的更新。现在假设得到一个新的迭代xk+1，并得到一个新的二次模型：
   
 
   
 
   
 
   
 
　　我们尽可能地利用上一步的信息来选取Bk。具体地，我们要求
 
　　从而得到
　　这个公式被称为割线方程。常用的拟牛顿法有DFP算法和BFGS算法。
 
 

3.1.3 共轭梯度法

共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。 在各种优化算法中，共轭梯度法是非常重要的一种。其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。
　　具体的实现步骤请参加wiki百科共轭梯度法。
　　下图为共轭梯度法和梯度下降法搜索最优解的路径对比示意图：
 
 
注：绿色为梯度下降法，红色代表共轭梯度法
　　MATLAB代码：
function [x] = conjgrad(A,b,x)
    r=b-A*x;
    p=r;
    rsold=r'*r;

    for i=1:length(b)
        Ap=A*p;
        alpha=rsold/(p'*Ap);
        x=x+alpha*p;
        r=r-alpha*Ap;
        rsnew=r'*r;
        if sqrt(rsnew)<1e-10
              break;
        end
        p=r+(rsnew/rsold)*p;
        rsold=rsnew;
    end
end


3.2 约束优化算法

3.2.1 含等式约束优化算法——拉格朗日乘数法

3.2.2 含不等式约束优化算法——KKT条件

 

4 智能优化算法 

 

4.1、遗传算法 

遗传算法（GeneticAlgorithm）是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法。

 

 

4.2、模拟退火算法 

是用来求解最优化问题的算法。比如著名的TSP问题，函数最大值最小值问题等等。

 

 

4.3、粒子群优化算法 

和模拟退火算法相似，它也是从随机解出发，通过迭代寻找最优解，它也是通过适应度来评价解的品质，但它比遗传算法规则更为简单，它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作，它通过追随当前搜索到的最优值来寻找全局最优。

 

 

4.4、蚁群算法 

蚁群算法(antcolony optimization, ACO)，又称蚂蚁算法，是一种用来在图中寻找优化路径的机率型算法。

 

 

4.5、免疫算法 

免疫算法是一种具有生成+检测 (generate andtest)的迭代过程的搜索算法。从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的。

 

 

4.6、克隆选择算法 

根据克隆选择原理设计的免疫算法。解决问题时，一般把问题定义为抗原，而问题的解就是抗体集合。在特定的形态空间中，随机产生的抗体试图与抗原发生匹配，即尝试解决问题。匹配度高的抗体有可能产生更好的解，被赋予更大的克隆概率参与下一次匹配。

 

 

4.7、和声搜索算法 

和声搜索（HarmonySearch, HS）算法是一种新颖的智能优化算法。类似于遗传算法对生物进化的模仿、模拟退火算法对物理退火的模拟以及粒子群优化算法对鸟群的模仿等，和声算法模拟了音乐演奏的原理。

 

 

4.8、禁忌搜索算法 

禁忌（TabuSearch）算法是一种亚启发式(meta-heuristic)随机搜索算法，它从一个初始可行解出发，选择一系列的特定搜索方向（移动）作为试探，选择实现让特定的目标函数值变化最多的移动。为了避免陷入局部最优解，TS搜索中采用了一种灵活的“记忆”技术，对已经进行的优化过程进行记录和选择，指导下一步的搜索方向，这就是Tabu表的建立。

 

 

4.9、差分进化算法 

它是由Storn等人于1995年提出的，和其它演化算法一样，DE是一种模拟生物进化的随机模型，通过反复迭代，使得那些适应环境的个体被保存了下来。但相比于进化算法，DE保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性。同时，DE特有的记忆能力使其可以动态跟踪当前的搜索情况，以调整其搜索策略，具有较强的全局收敛能力和鲁棒性，且不需要借助问题的特征信息，适于求解一些利用常规的数学规划方法所无法求解的复杂环境中的优化问题。

 

 

4.10、BP神经网络算法 

BP神经网络是一种基于有监督的学习，使用非线性可导函数作为传递函数的前馈神经网络。

 

 

5 算法比较

5.1 无约束优化算法

Ø  坐标轮换法具有不需要导数信息的优点，计算过程比较简单，程序实现也比较容易，但存在算法收敛速度较慢、计算效率低等缺点。坐标轮换法主要用来解决优化问题设计变量数目小于10的小规模无约束优化问题;另外，坐标轮换法还可解决目标函数的等值线为圆或平行于坐标轴的优化问题。

Ø  与其他无约束优化算法相比，最速下降法具有方法简单等优点，计算效率在最初几步迭代时较高，且对初始点不敏感，因而常与其他方法一起使用，但最速下降法需要目标函数的一阶导数信息。

Ø  求解无约束优化问题的牛顿法对给定的初始点比较敏。如果初始点选择的比较好，则其解决优化问题的收敛过程会很快;如果选择不当，则可能会出现收敛失败的情况。另外，牛顿法存在计算过程复杂、计算量特别大等缺点，因此主要适合于设计变量数目小的优化问题及目标函数阶次较低的优化问题。

Ø  共轭梯度法具有收敛速度快等优点，其收敛速度远快于最速下降法。共轭梯度法计算简单，所需要的存储空间少，适合于优化变量数目较多的中等规模优化问题。

Ø  在无约束优化方法中，Powell法是计算效率比较高的优化算法之一，它不需要目标函数的导数，是求解中小型规模优化问题的有效方法。

Ø  变尺度法也是计算效率比较高的优化算法之一，可用来解决高阶目标函数的优化问题，但存在程序实现比较复杂、存储空间比较大等缺点。

Ø  单纯形法具有不需目标函数导数信息、程序实现简单、计算效率比较高等优点。

 

5.2 约束优化算法

 

Ø  Monte Carlo法具有方法简单、不需要导数信息等优点，但存在求解高维优化问题时计算量大等不足;

Ø  随机方向搜索法具有优化求解过程收敛快，但存在局部寻优的不足，因而在使用时需采用选择多个不同初始点的策略;

Ø  复合形法具有程序实现简单等优点，但在解决设计变量和约束条件多的优化问题时优化效率比较低;

Ø  可行方向法是解决约束优化问题的有效方法之一，适合求解中等规模化问题，但存在程序实现复杂等不足;

Ø  广义简约梯度法具有算法收敛快、计算精度高等优点，但也存在程序实现复杂等不足;

Ø  罚函数优化方法包括内点法、外点法、混合法等，具有方法实现简单等优点，但存在优化过程不稳定、收敛速度较慢等缺点，适宜于解决中小规模优化问题;

Ø  序列线性规划法收敛较慢，只适用于非线性程度不是很强的优化问题;

Ø  序列二次规划法是收敛速度较快、优化比较有效的方法之一，比较适合于中等规模优化问题;

5.3 智能算法

遗传算法：优点是能很好的处理约束，能很好的跳出局部最优，最终得到全局最优解，全局搜索能力强；缺点是收敛较慢，局部搜索能力较弱，运行时间长，且容易受参数的影响。

遗传算法适合求解离散问题，具备数学理论支持，但是存在着汉明悬崖等问题。

 

模拟退火：优点是局部搜索能力强，运行时间较短；缺点是全局搜索能力差，容易受参数的影响。

 

爬山算法：显然爬山算法较简单，效率高，但是处理多约束大规模问题时力不从心，往往不能得到较好的解。

 

粒子群算法适合求解实数问题，算法简单，计算方便，求解速度快，但是存在着陷入局部最优等问题。

 

蚁群算法适合在图上搜索路径问题，计算开销会大。

 

要将三种算法进行混合，就要针对特定问题，然后融合其中的优势，比如将遗传算法中的变异算子加入粒子群中就可以形成基于变异的粒子群算法。

 https://blog.csdn.net/acelit/article/details/63685878

posted @ 2019-01-28 22:43  yumoye  阅读(3969)  评论(0)  编辑  收藏  举报