第三章 计算机进行小数运算出错的原因
3.1 将0.1累加100次也得不到10
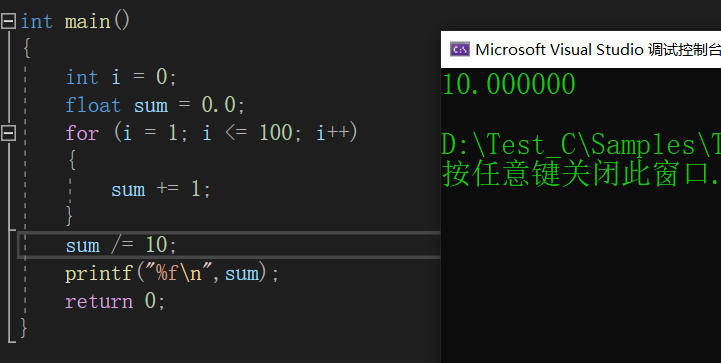
本章学习之初，先给大家出个小题目吧，请问以下程序的运行结果是多少？
1 #include <stdio.h>
2 int main()
3 {
4 int i = 0;
5 float sum = 0.0;
6 for (i = 1; i <= 100; i++)
7 {
8 sum += 0.1;
9 }
10 printf("%f\n",sum);
11 return 0;
12 }
如果你以为计算出来的结果是10，那你就做错了，正确答案是10.000002，不信的话请看
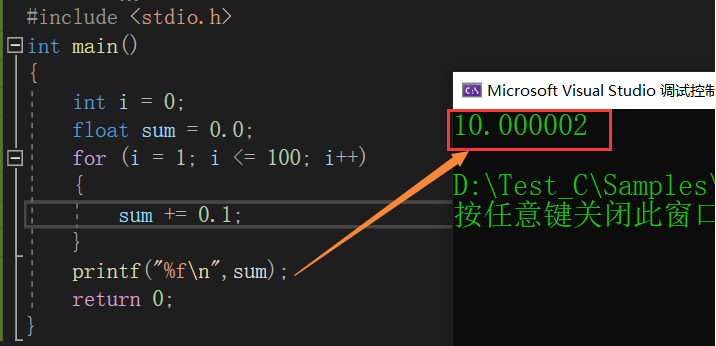
第一次我看到结果的那一刹那也是一脸疑惑，这计算机还会出错啊，直到我仔细阅读了本章的内容，内心的谜团才得以解开，如果屏幕前的你也和我一样好奇计算机出错的原因，那就请仔细往下读吧！
3.2 用二进制数表示小数
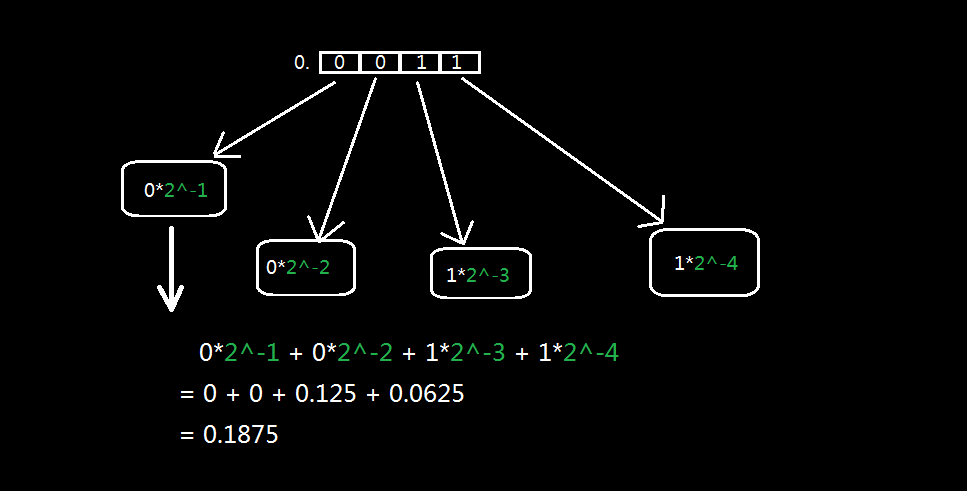
在上一章中，我们对整数里边的二进制数与十进制数之间的相互转换进行了详细的说明。其实二进制小数转换成十进制数的方法和整数的处理方式是一样的——将各数位的数值与该数位所对应的位权相乘，然后将相乘的结果相加即可。这理论看着有点儿难懂，在此处特地准备了一个例子进行说明，如下便是将二进制小数0.0011转换成十进制数的方法，其中绿色字体部分代表的就是位权：
不过本小节中作者并没有对十进制小数转换成二进制小数进行阐述，但我觉得还是有必要了解一下的。然后我又从网上查找了相关的十进制小数转换成二进制小数的方法，其处理方式是：当整数部分为0时，不断对该小数进行乘2取整操作，直到整数部分为1，小数部分全为0；如果在不断乘2的过程中出现了整数部分为1，但是小数部分不全为0的现象，则下次整数部分取0继续乘2取整。最后顺序输出取整的数字即可~，内个，请大家原谅我这菜鸡般的语言总结能力，事实上并不复杂，姑且将就着理解一下,下边咱们通过两个例子可能就会了：
eg1——
eg2——
3.3 计算机运算出错的原因
理解了上边3.2的内容，我们再来回答3.1中计算机为什么会出错——那是因为有些十进制小数是没有办法用二进制小数正确表示的。比如十进制小数0.1，对其转换成二进制小数的过程中会不断对其小数部分进行乘2取整操作，它的小数部分只会是1、2、4、8、6、2、4、6、8……不断地循环，小数部分永远也不会变为全0。因为计算机是个有限的机器设备，是没有办法处理无限循环小数的，只能得到它的近似值。比如说像十进制小数0.1转换成二进制数就是0.00011001100...这样的二进制小数。
如下二进制小数 0.0000~0.0011
| 二进制数 | 十进制数 |
| 0.0000 | 0 |
| 0.0001 | 0.0625 |
| 0.0010 | 0.0125 |
| 0.0011 | 0.1875 |
如表格中所示那样，二进制数0.0000到0.0001只是加上了0.0001，但是对于十进制数却是加上了0.0625，也就是说，对于十进制数0~0.0625之间的数是无法用二进制小数准确地表示的。
3.4 什么是浮点数
浮点数，字面上的意思好像是小数点可以浮动的小数，实际上的意义也的确如此。既然有浮点数，盲猜一下是不是还有定点数呢？没错，还真有，比如说像十进制数0.1875，0.0125，0.0625......等等，小数点的位置固定不变的数即为定点数，而像0.1875可以（用科学计数法）写成0.01875×101、0.001875×102、亦或写成1.875×10-1、18.75×10-2等等多种方式，通过这种方法我们既改变了小数点的相对位置，并且还没有改变它的值的数就可以称之为浮点数。通过以上内容大家应该对浮点数有一定的了解了，对于浮点数官方给出的定义是：用符号、尾数、基数（进制）和指数这四部分表示的的小数。
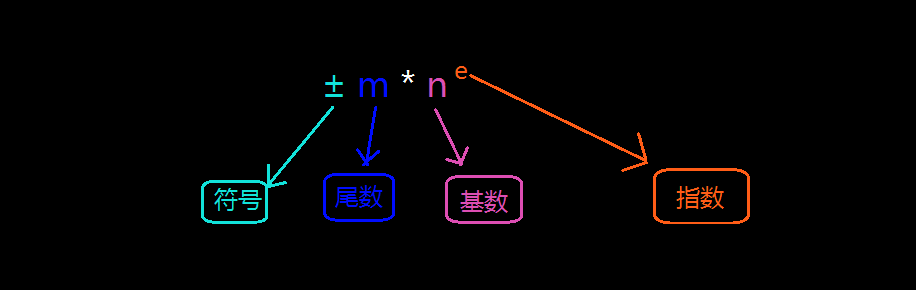
很多的编程语言都把浮点数分为两类：单精度浮点数（float）、双精度浮点数（double），其中单精度浮点数用32位数来表示全体小数，双精度浮点数用64位数来表示全体小数，如下便是单精度浮点数的表示方法，也就是所谓的IEEE（美国电气工程协会）标准：
1位符号部分：用1表示负数，用0表示正数；
8位指数部分：采用EXCESS系统表现；
23位尾数部分：将小数点前边的值固定为1的正则表达式。
64位双精度浮点数的表示方法和32位单精度浮点数的表述方法类似，不同的是位长变了，符号部位仍为1位，指数为11位，尾数部分为52位。此处就不再作图演示了。
3.5 正则表达式和EXCESS系统
正则表达式
首先我想吐槽一下这个翻译哈——“正则表达式”，这个翻译的新术语给人的感觉很费解，甚至让人根本不知所云（虽然我也想不出更好的翻译哈）。但是我觉得我们可以通过英文原词可以更好地理解这个术语，英语中的正则表达式叫作“regular expression”,其中regular的意思有：规律，恒定的，规则的；expression的意思有：表达，表示方法。大概的意思就是说：有规律的，或者说是恒定的表示方法，个人感觉有点秦始皇统一度量衡内味儿。具体到应用中，举个栗子你就明白了，例如计算4 ÷ 3 = ？，结果我们可以写成假分数的形式:4/3,或带分数的形式：1又1/3,亦或是无限循环小数形式：1.33...,而此时规定了，要求统一写成小数形式，保留两位小数，那么结果只能是1.33，假分数、带分数以及无限循环小数的表示形式虽说仍然正确，但是它们却不在符合要求了，而这个规定就可以称之为“regular expression”,也就是那个不太好理解的术语——“正则表达式”。
同样的，在3.4中所表示的浮点数0.1875×101可以写成多种形式，那么将小数点前边的值固定为1的正则表达式即为1.875×10-1。通过这种方式，就可以使得每一个浮点数小数点的前一位的值均为1，这样便可以省略掉这一个数据位来表示更大范围一点儿的数据。
EXCESS系统
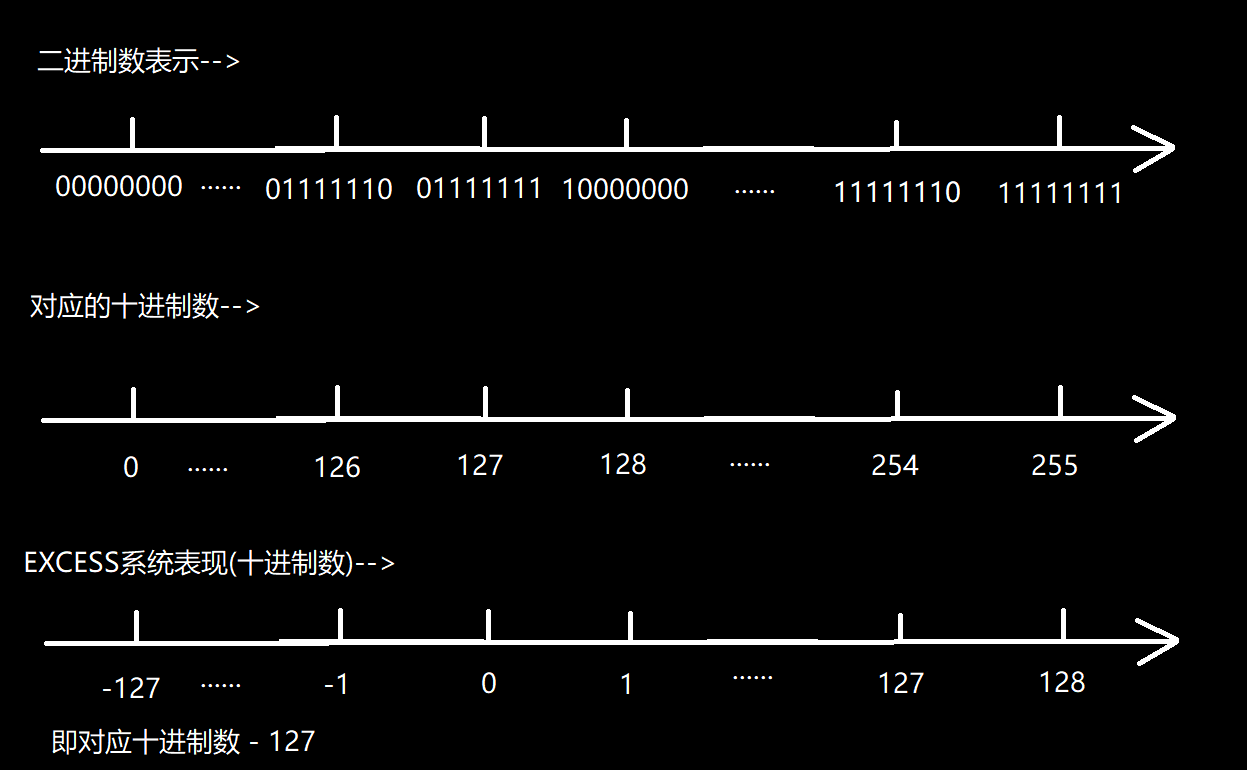
请大家再来看一下这张图片
我们知道，在单精度浮点数里边，指数部分是由 8位 二进制数构成的，可以表示的范围是00000000~11111111，转换成十进制数就是0~255（此处不考虑符号位，因为符号位由第一位决定，指数部分可以理解为全都是正数的数），可是在实际的应用中我们知道，指数部分的e是完全有可能为负数的，为了解决这一问题，EXCESS系统应运而生：它通过将指数范围的中间值127（255 / 2 省略小数位）设为0，使得指数部分不需要通过使用符号位来表示负数。说白了，其目的就是为了让指数e部分可以表示负数，如下图所示：
3.6 在实际的程序中进行确认
说了那么多，小数在内存中到底是不是按照EXCESS的方式进行存储的呢？我们举个栗子来测试一下，比如十进制小数0.75（按照单精度浮点数进行处理）。我们先将其转换为二进制小数为：0.1100，写成小数点前一位是1的正则表达式形式为：
1.1 × 2-1可知该数：
符号位为：0；
基数为：2；
指数为（EXCESS系统表现）：126 - 127 = -1；
尾数为：10000000 00000000 00000000 000。
所以十进制小数0.75表示成单精度浮点数在内存中的存储方式应该是这样的（“-”是为了分隔各个部分）：
0--01111110--10000000 00000000 0000000
不过可能是由于印刷或者是翻译等的问题，本小节中的程序示例是有谬误的，书中的示例程序是这样的：
1 #include <stdio.h> 2 #include <string.h> 3 int main() 4 { 5 float data; 6 unsigned long buff; 7 int i; 8 char s[34]; 9 10 data = (float)0.75; 11 12 memcpy(&buff, &data, 4); 13 //memcpy(void* dest, void* src, size_t)内存拷贝函数，将单精度浮点型data在内存中的表示形式拷贝到buff里边，
//最后一个参数为4因为float类型在内存中占据4个字节 14 for (i = 33; i >= 0; i--) 15 { 16 if (i == 1 || i == 10) 17 { 18 s[i] = '-'; 19 } 20 else 21 { 22 if (buff % 2 == 1) 23 { 24 s[i] = '1'; 25 } 26 else 27 { 28 s[i] = '0'; 29 } 30 buff /= 2; 31 } 32 } 33 s[34] = '\0'; 34 printf("%s\n", s); 35 36 return 0; 37 }
这段代码在编写阶段就报了两个警告：
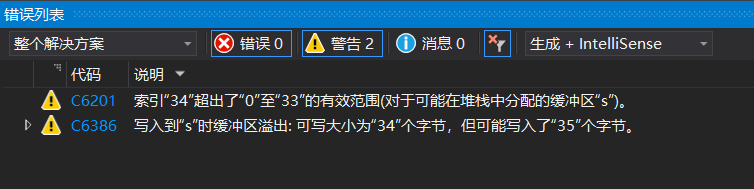
并且程序运行结束后什么也没有打印，这个警告应该是访问越界了，仔细读了读程序才找到编译器报警告的原因——果真是数组访问越界的问题，大家再看上边程序第8行红色加粗字体部分，表示定义一个字符数组，该数组可以存放34个字符型元素，但是到第33行的时候是把 '\0' 这个字符赋值给下标为34的元素，下标为34则为数组的第35个元素，因此我将第8行的 char s[34] 改为 char s[35],警告便消除了，编译通过，运行出来的结果如下——>
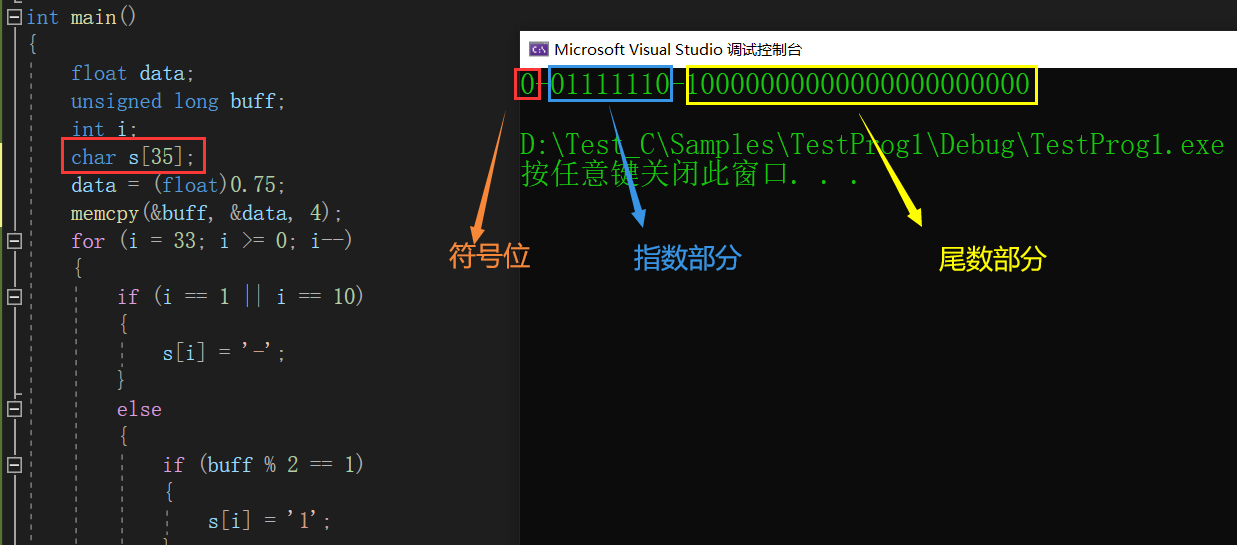
这刚好与我们之前算出的数字吻合！
3.7 如何避免计算机计算出错
策略一：回避错误，即无视这些极其微小的误差。不过这个策略乍一听觉得这很荒唐——回避错误也叫避免错误呃......,事实上,在现实的生活中，我们无法做到每一个零部件能真正地做到那么精确无误，让100个0.1㎜长的零部件合起来为长为10.000002㎝，其实完全是可以接受的。这些细小的误差可以忽略不计。不过这个地方说成回避的确有点不太合适，叫做 允许错误 或许更好点。
策略二：将小数化为整数进行计算，因为整数都是可以用二进制数表示的，这种做法适合纯粹的数值运算。比如同样是100个0.1相加，我们可以让每一个数都乘以10，再将求得的结果除以10即可算出正确的结果。
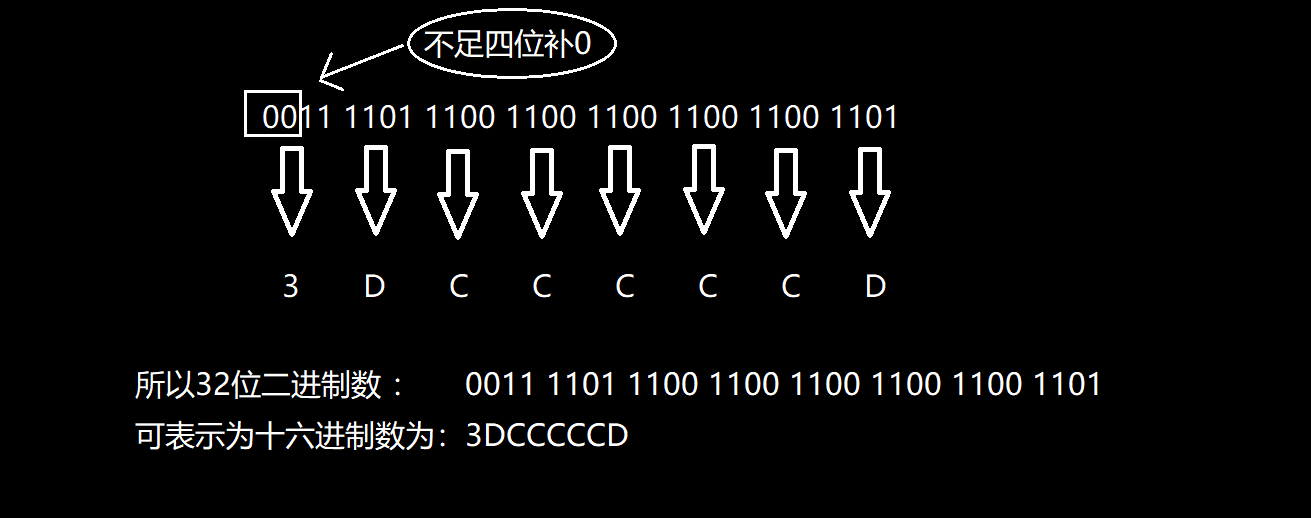
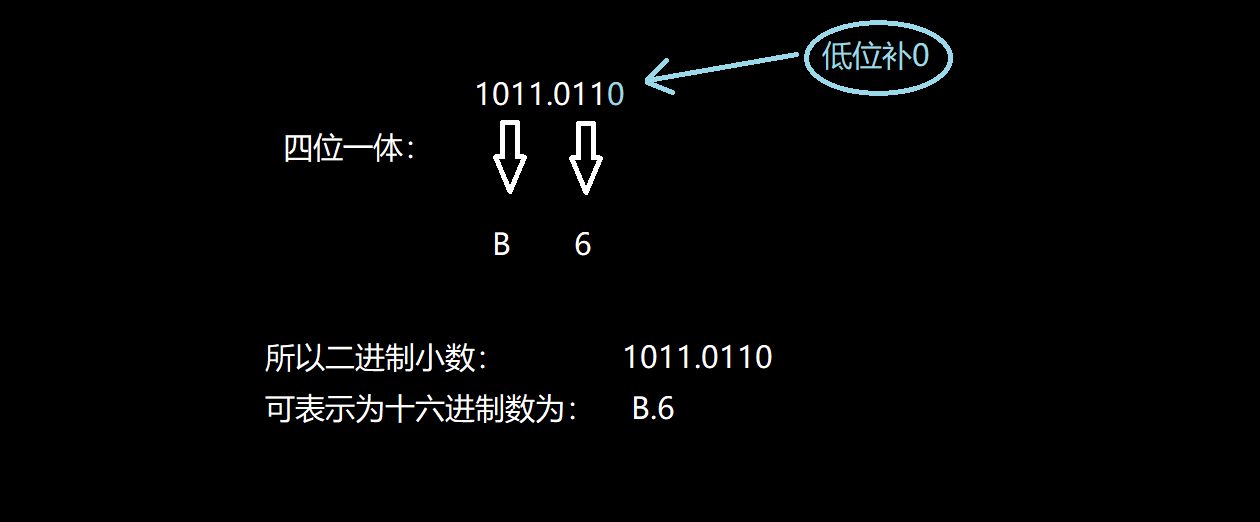
3.8 二进制数表示十六进制数
二进制与十六进制表示法，其中为 0000 ~ 1111 的表示形式：
| 二进制数 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 十六进制数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 二进制数 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 十六进制数 | 8 | 9 | A/a | B/b | C/c | D/d | E/e | F/f |
看懂这个表示方法，我们也就能理解了为什么1个十六进制数可以表示4个二进制数了。
说实话本章节理解起来难度加大了不少，尤其是到正则表达式和EXCESS表现哪里卡了好久，在加上出现了比较多的新术语，并且在程序验证那里书中还出现了错误，再加上又做了好几张图，为了不误人子弟，又对这篇博客前前后后修修改改用了快两天的时间了。当然了，吐槽归吐槽，收获也是颇丰的！如果文中有帮助到大家的地方，还请各位点个免费的赞呐，嘿嘿嘿😊
以上便是第三章的读书笔记和心得体会，由于毕竟个人技术有限，文中难免有纰漏之处，在此也欢迎各位读者留言批评指正。
