python递归函数与二分查找
函数的嵌套
函数的嵌套其实就与if、while、for循环的嵌套一样,这里只做简单展示。
# 函数嵌套死循环
def index():
func()
print('来自index')
def func():
index()
print('来自func')
func()
递归函数
在编程语言中,函数直接或间接调用函数自身,则该函数称为递归函数。
基本演示
# 直接调用自身
def index():
print(1)
# 在函数内部调用了自身
index()
index()
# 间接调用自身
def a():
print('a')
# a函数中调用b函数
b()
def b():
print('b')
# b函数中调用a函数
a()
a()
简单的来说,就是套娃,但是要注意,递归函数最好有个可以让它结束继续递归的条件,不然python解释器就会报错。

这段报错说明你的函数超过了最大递归深度,也可以说是最大递归次数,超过了这个次数就会报错
斐波那契数列
一个数列如果它的前2项数值为1,从第三项开始每一项等于前2项之和,那么这个数列称为斐波那契数列。
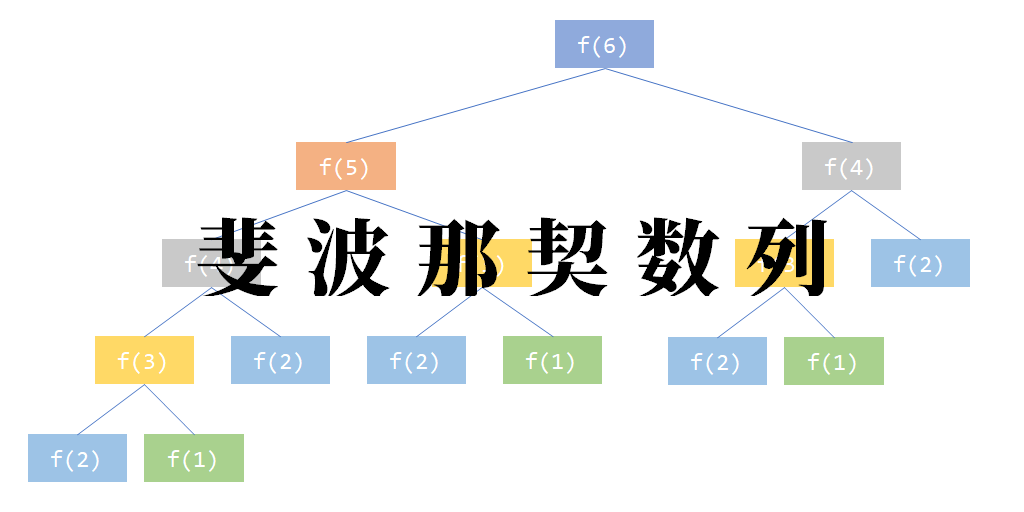
代码实现:
def f(a):
# 前2项为1
if a <= 2:
return 1
# 每一项等于前2项之和
res = f(a - 1) + f(a - 2)
return res
print(f(6)) # 结果:8
总结
- 递归就是函数直接或间接调用自身
- 递归一定要有可以结束的条件
- 递归过程中,每进行一次递归都要离结束近一点

小拓展
获取默认最大递归深度
import sys
print(sys.getrecursionlimit())
修改最大递归深度
sys.setrecursionlimit(2000)
算法之二分法
在了解二分法之前,我们得先了解什么是算法。
算法其实就是解决问题的有效方法,在大多数情况下,它可以让问题的解决更加的迅速。
简介
我们在查找列表中某一个值的所在位置的时候,除了使用index()函数外,在没有接触算法之前,最简单易懂是不是就是将列表中的元素遍历一遍,一个个比较过去?
这种方法只能作用在比较小的列表中,那如果遇到了有着几十万元素的列表的时候,我们就无法使用这种遍历的方法了,这时候就可以使用二分法了。

二分法:对一个已经排序好的数据集从1/2处开始查找。
如果是降序数据集:如果比1/2处的值大了,去掉右边的数据,去比对左边的1/2处;如果比1/2的值小了,去掉左边的数据,去比对右边的1/2处;直到找到为止。
如果是升序数据集:如果比1/2处的值大了,去掉左边的数据,去比对右边的1/2处;如果比1/2的值小了,去掉右边的数据,去比对左边的1/2处;直到找到为止。
举例
找到[1, 2, 3, 4, 5, 6, 7, 8, 9]中的3
"""普通二分法查找"""
l = [1, 2, 3, 4, 5, 6, 7, 8, 9]
def get_target(l1, target_num):
i = 0
j = len(l1)
while i != j:
# 列表的1/2处
half_l1 = (i + j) // 2
if l1[half_l1] == target_num:
print('找到了!在第%s个' % (half_l1 + 1))
break
elif target_num > l1[half_l1]:
# 如果值比1/2处的大,查找范围变为[half_l1:j]
i = half_l1 + 1
else:
# 如果值比1/2处的小,查找范围变为[i:half_l1]
j = half_l1
else:
# 直到i == j了都没找到说明没有这个值
print('没找到!')
get_target(l, 3)
"""递归二分法查找"""
l = [1, 2, 3, 4, 5, 6, 7, 8, 9]
def get_target(l1, target_num):
if len(l1) == 0:
print('没找到!')
return
# 列表的1/2处
half_l1 = len(l1) // 2
if target_num == l1[half_l1]:
print('找到了!')
elif target_num > l1[half_l1]:
# 如果比1/2处的值大了,去掉左边的数据,去比对右边的1/2处
get_target(l1[half_l1 + 1:], target_num)
else:
# 如果比1/2处的值小了,去掉右边的数据,去比对左边的1/2处
get_target(l1[:half_l1], target_num)
get_target(l, 30)
总结
二分查找虽然在数据大的情况下查找更为迅速,但也有缺陷:
- 数据集必须为升序或降序
- 如果要查找的元素在数据的开头,二分查找更为复杂


