矩阵变换、矩阵求值
对一个矩阵进行某种运算和操作,其结果还是一个矩阵。
对角阵
三角阵
矩阵的转置
矩阵的旋转
矩阵的翻转
矩阵求逆等等
1.对角阵
对角阵:只有对角线上有非零元素的矩阵。
数量矩阵:对角线上的元素相等的对角矩阵。
单位矩阵:对角线上的元素都为1的对角矩阵。
(1) 提取矩阵的对角线元素
diag(A):提取矩阵A主对角线元素,产生一个列向量。
diag(A,k):提取矩阵A第k条对角线的元素,产生一个列向量。
对角线如下:

(2) 构造对角阵
diag(V):以向量 V为主对角线元素,产生对角矩阵。
diag(V,k):以向量 V为第k条对角线元素,产生对角矩阵。
例子:先建立5×5矩阵A,然后将A的第一行元素乘以1,第二行乘以2,…,第五行乘以5。
>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]
A = 7 0 1 0 5
3 5 7 4 1
4 0 3 0 2
1 1 9 2 3
1 8 5 2 9
>> D=diag(1:5); //对角线元素为12345
>> D*A //对角阵左乘一个矩阵时,即矩阵对角线的第一个元素,乘以该矩阵的第一行。
ans = 7 0 1 0 5
6 10 14 8 2
12 0 9 0 6
4 4 36 8 12
5 40 25 10 45
要将A的各列元素分别乘以对角阵的对角线元素,如何实现?——对角阵右乘矩阵A
要将A的各列元素分别乘以对角阵的对角线元素,可以用一个对角阵右乘矩阵A。
>> A=[7,0,1,0,5;3,5,7,4,1;4,0,3,0,2;1,1,9,2,3;1,8,5,2,9]
A = 7 0 1 0 5
3 5 7 4 1
4 0 3 0 2
1 1 9 2 3
1 8 5 2 9
>> D=diag(1:5);
>> A*D
ans =7 0 3 0 25
3 10 21 16 5
4 0 9 0 10
1 2 27 8 15
1 16 15 8 45
2.三角阵
上三角阵:矩阵的对角线以下的元素全为零的矩阵。
下三角阵:对角线以上的元素全为零的矩阵。
(1)上三角矩阵
triu(A):提取矩阵A的主对角线及以上的元素。
triu(A,k):提取矩阵A的第k条对角线及以上的元素。
>> triu(ones(4),-1) //ones产生四阶全1矩阵
ans =1 1 1 1
1 1 1 1
0 1 1 1
0 0 1 1
(2) 下三角矩阵
在MATLAB中,提取矩阵A的下三角矩阵的函数是tril,其用法与triu函
数完全相同。
3.矩阵的转置
原矩阵的第一行变成目标矩阵的第一列,以此类推。
转置运算符是小数点后面接单引号(.')。
共轭转置,其运算符是单引号('),它在转置的基础上还要取每个数的复共轭。
>> A=[1,3;3+4i,1-2i]
A = 1.0000 + 0.0000i 3.0000 + 0.0000i
3.0000 + 4.0000i 1.0000 - 2.0000i
>> A.'
ans =1.0000 + 0.0000i 3.0000 + 4.0000i
3.0000 + 0.0000i 1.0000 - 2.0000i
>> A'
ans =1.0000 + 0.0000i 3.0000 - 4.0000i
3.0000 + 0.0000i 1.0000 + 2.0000i
矩阵的转置:把源矩阵的第一行变成 目标矩阵的第一列,第二行变成第二 列,…,依此类推。
如果矩阵的元素是实数,那么转置和共轭转置的结果是一样的。
4.矩阵的旋转
rot90(A,k):将矩阵A逆时针方向旋转90º的k倍,当k为1时可省略。
>> A=[1,3,2;-3,2,1;4,1,2]
A = 1 3 2
-3 2 1
4 1 2
>> rot90(A)
ans =2 1 2
3 2 1
1 -3 4
>> rot90(A,2)
ans =2 1 4
1 2 -3
2 3 1
5.矩阵的翻转
对矩阵实施左右翻转是将原矩阵的第一列和最后一列调换,第二列和倒数第二列调换,…,依此类推。
fliplr(A):对矩阵A实施左右翻转。
flipud(A):对矩阵A实施上下翻转。 //将原矩阵的第一行和最后一行调换,第二行和倒数第二行调换,…,依此类推。
例2 验证魔方阵的主对角线、副对角线元素之和相等。
>> A=magic(5);
>> D1=diag(A); //提取A的主对角线生成D1
>> sum(D1)
ans = 65
>> B=flipud(A); //上下翻转 副对角线变成主对角线
>> D2=diag(B);
>> sum(D2)
ans = 65
对矩阵A实施上下翻转得到矩阵B,这样A的副对角线就移到了B的主对角线
5阶魔方阵的主对角线、副对角线元素之和相等,都为65。
6.矩阵的求逆
l 对于一个方阵A,如果存在一个与其同阶的方阵B,使得AB=BA=I (I为单位矩阵),则称B为A的逆矩阵,当然,A也是B的逆矩阵。
l inv(A):求方阵A的逆矩阵。
例3 用求逆矩阵的方法解线性方程组。
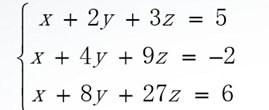
在线性方程组Ax=b两边各左乘A-1,得x=A-1b。
>> A=[1,2,3;1,4,9;1,8,27];
>> b=[5;-2;6];
>> x=inv(A)*b
x = 23.0000 -14.5000 3.6667
>> x=A\b //利用左除求线性方程组
x = 23.0000 -14.5000 3.6667
2.3矩阵求值
矩阵的行列式值 矩阵的秩 矩阵的迹 矩阵的范数 矩阵的条件数
1.方阵的行列式
把一个方阵看作一个行列式,并对其按行列式的规则求值,这个值就称为所对应的行列式的值。
det(A):求方阵A所对应的行列式的值。
例1 验证det(A-1)=1/det(A)。
>> format rat
>> A=[1,3,2;-3,2,1;4,1,2]
A =
1 3 2
-3 2 1
4 1 2
>> det(inv(A))
ans =1/11
>> 1/det(A)
ans = 1/11
2.矩阵的秩
矩阵线性无关的行数或列数称为矩阵的秩。
rank(A):求矩阵A的秩。
例2 求3~20阶魔方阵的秩。
for n=3:20
r(n)=rank(magic(n)); //每循环一次产生魔方阵并求秩
end
bar(r) //绘制直方图
grid on
axis([2,21,0,20])
[3:20;r(3:20)]


分为三类:
奇数阶魔方阵秩为n,即奇数阶魔方阵是满秩矩阵。
一重偶数阶魔方阵秩为n/2+2(n是2的倍数,但非4的倍数)。
双重偶数阶魔方阵秩均为3 (阶数是4的倍数)。
3.矩阵的迹
矩阵的迹等于矩阵的对角线元素之和,也等于矩阵的特征值之和。
trace(A):求矩阵A的迹。
>> A=[1,3,2;-3,2,1;4,1,2]
A =1 3 2
-3 2 1
4 1 2
>> b = trace(A) //求矩阵的迹
b = 5
>> t = sum(diag(A)) //提取主对角线元素在求和
t = 5
4.向量和矩阵的范数
矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。
(1)向量的3种常用范数
设向量v含有n个元素。

在MATLAB中,求向量范数的函数为:
norm(V)或norm(V,2):计算向量V的2—范数。
norm(V,1):计算向量V的1—范数。
norm(V,inf):计算向量V的∞—范数。
(2)矩阵的范数
从属于3中向量范数,矩阵的范数计算公式如下:

MATLAB提供了求3种矩阵范数的函数,其函数调用格式与求向量的范数的函数完全相同。
>> x=[2 0 1;-1 1 0;-3 3 0]
x = 2 0 1
-1 1 0
-3 3 0
>> n = norm(x) //二范数
n = 4.7234
>> n = norm(x,1) //一范数
n = 6
5.矩阵的条件数——描述矩阵性能
矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积。
条件数>1,条件数越接近于1,矩阵的性能越好,反之,矩阵的性能越差。
在MATLAB中,计算矩阵A的3种条件数的函数是:
cond(A,1):计算A的1—范数下的条件数。
cond(A)或cond(A,2):计算A的2—范数数下的条件数。
cond(A,inf):计算A的∞—范数下的条件数。
例3 求2~10阶希尔伯特矩阵的条件数。
for n=2:10
c(n)=cond(hilb(n));
end
format long
c'

随着阶数的增加,希尔伯特矩阵的条件数不断增大,矩阵性能变差。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号