MATLAB矩阵的表示
矩阵是matlab中最基本的数据对象。
l 矩阵的建立
l 冒号表达式
l 结构矩阵和单元矩阵
1.矩阵的建立
（1）利用直接输入法建立矩阵:将矩阵的元素用中括号括起来，按矩阵行的顺序输入各元素，同一行的各元素之间用逗号或空格分隔，不同行的元素之间用分号分隔。
>> A=[1,2,3;4,5,6;7,8,9]
A = 1 2 3
4 5 6
7 8 9
（2）利用已建好的矩阵建立更大的矩阵:一个大矩阵可以由已经建立好的小矩阵拼接而成。
>> A=[1,2,3;4,5,6;7,8,9];
>> B=[-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C=[A,B;B,A]
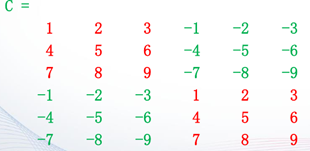
还可以用实部矩阵和虚部矩阵构成复数矩阵
>>B=[1,2,3;4,5,6];
>>C=[6,7,8;9,10,11];
>>A=B+i*C
A为同型矩阵，B为实部，C为虚部。i*C表示数与矩阵相乘。
2.冒号表达式
向量是矩阵的特殊类型，用：产生行向量。
如果省略步长e2，则步长为1。例如，t=0:5与t=0:1:5等价。
>> t=0:1:5
t = 0 1 2 3 4 5
还可以用linspace产生行向量。
当n省略时，自动产生100个元素。
>> x=linspace(0,pi,6)
x = 0 0.6283 1.2566 1.8850 2.5133 3.1416
3．结构矩阵和单元矩阵
（1）结构矩阵——把一组数据类型不同而逻辑上相关的数据组成一个有机的整体。
由结构数据构成的矩阵就是结构矩阵，结构矩阵里的每个元素就是结构数据类型。
格式为：
结构矩阵元素.成员名=表达式
就是给结构矩阵中的每个元素的每个成员分别赋值。
>> a(1).x1=10; a(1).x2='liu'; a(1).x3=[11,21;34,78];
>> a(2).x1=12; a(2).x2='wang'; a(2).x3=[34,191;27,578];
>> a(3).x1=14; a(3).x2='cai'; a(3).x3=[13,890;67,231];
（2）单元矩阵——每个元素可以由不同的数据类型组成的
建立单元矩阵和一般矩阵相似，直接输入就可以了，只是单元矩阵元素用大括号括起来
>> b= {10,'liu',[11,21;34,78];12,'wang',[34,191;27,578];... 14,'cai',[13,890;67,231]}
b =
[10] 'liu' [2x2 double]
[12] 'wang' [2x2 double]
[14] 'cai' [2x2 double]
1.5矩阵元素的引用
l 矩阵元素的引用方式
l 利用冒号表达式获得子矩阵
l 利用空矩阵删除矩阵的元素
l 改变矩阵的形状
1．矩阵元素的引用方式 //下标为必须为正整数，且用圆括号括起来
（1）通过下标来引用矩阵的元素
A(3,2)表示A矩阵第3行第2列的元素。
>> A(3,2)=200
例：
>> A=[1,2,3;4,5,6];
>> A(4,5)=10
A = 1 2 3 0 0
4 5 6 0 0
0 0 0 0 0
0 0 0 0 10
注意：如果给出的行下标或列下标大于原来矩阵的行数和列数， 那么MATLAB将自动扩展原来的矩阵，并将扩展后没有赋值的矩阵元素置为0。
（2）通过序号来引用
l 在MATLAB中，矩阵元素按列存储，即首先存储矩阵的第一列元素，然后存储第二列元素，…，一直到矩阵的最后一列元素。
l 矩阵元素的序号就是矩阵元素在内存中的排列顺序。
例“”
>> A=[1,2,3;4,5,6]
A = 1 2 3
4 5 6
>> A(3)
ans = 2 //a12是第三号元素
序号与下标是一一对应的，以m×n矩阵A为例，矩阵元素A(i,j)的序 号为(j-1)×m+i
矩阵元素的序号与下标可以利用sub2ind和ind2sub函数实现转换。
sub2ind函数：将矩阵中指定元素的行、列下标转换成存储的序号。调用格
式为：
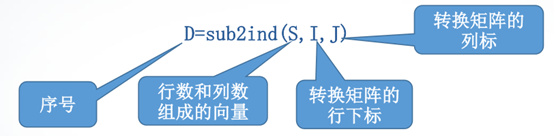
sub2ind函数举例。
>> A=[1:3;4:6]
A = 1 2 3
4 5 6
>> D=sub2ind(size(A),[1,2;2,2],[1,1;3,2]) //i，j为矩阵，多个元素的行列下标转化为存储序号D与ij相同
D = 1 2
6 4
ind2sub函数：将把矩阵元素的序号转换成对应的下标，其调用格式为：
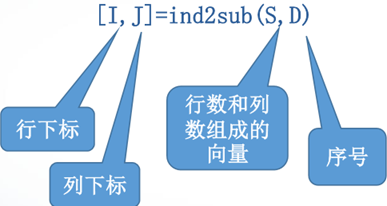
ind2sub函数举例。
>> [I,J]=ind2sub([3,3],[1,3,5])
I = 1 3 2
J = 1 1 2
2．利用冒号表达式获得子矩阵
子矩阵是指由矩阵中的一部分元素构成的矩阵。用单个：作为行/列下标，代表全部行/列。
A(i,:) 第i行的全部元素
A(:,j) 第j列的全部元素
A(i:i+m,k:k+m) 第i～i+m行内且在第k～k+m列中的所有元素
A(i:i+m,:) 第i～i+m行的全部元素
例子：
>> A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15]
A = 1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
>> A(1:2,:)
ans = 1 2 3 4 5
6 7 8 9 10
>> A(2:3,1:2:5)
ans = 6 8 10
11 13 15
end运算符：表示某一维的末尾元素下标。
>>A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20];
>>A(end,:) //引用最后一行元素
ans = 16 17 18 19 20
>> A([1,4],3:end) //引用第一行和第四行的从第三列到最后一列的元素
ans = 3 4 5
18 19 20
3．利用空矩阵删除矩阵的元素
空矩阵是指没有任何元素的矩阵。
>> x=[]
x = []
X是一个空矩阵。
>> A=[1,2,3,0,0;7,0,9,2,6;1,4,-1,1,8]
A = 1 2 3 0 0
7 0 9 2 6
1 4 -1 1 8
>> A(:,[2,4])=[] //删除某些元素置位空矩阵就好了2和4列
A = 1 3 0
7 9 6
1 -1 8
4．改变矩阵的形状
reshape(A,m,n)：在矩阵总元素保持不变的前提下，将矩阵A重新排成m×n的二维矩阵。
注意：reshape函数只是改变原矩阵的行数和列数，但并不改 变原矩阵元素个数及其存储顺序。
>> x=[23,45,65,34,65,34,98,45,78,65,43,76];
>> y=reshape(x,3,4)
Y= 23 34 98 65
45 65 45 43
65 34 78 76
A(:) ：将矩阵A的每一列元素堆叠起来，成为一个列向量。
>> A =[-45,65,71;27,35,91]
A = -45 65 71
27 35 91
>> B=A(:)
B =
-45
27
65
35
71
91
即：A(:)等价于reshape(A,6,1)。
