12.高斯消去法（1）——矩阵编程基础

 　　对于一阶线性方程的求解有多种方式，这里将介绍利用高斯消去法解一阶线性方程组。在介绍高斯消去法前需要对《线性代数》做一下温习，同时在代码中对于矩阵的存储做一个简要介绍。

　　通常遇到矩阵我们会利用二维数组来进行对矩阵数值的存储（例如前几篇中动态规划中对于求解矩阵初始化就是利用二维数组），但在计算机的内存中是没有“二维”这种存储方式的，内存都是以“一维”的方式存储数据，那么这就带来一个问题，在代码层面定义一个二维数组时，计算机内部是怎么存储的呢？

int[][] array = new int[3][3]; //Java中定义一个3行3列的矩阵

　　Java中的二维数组定义在内存中实际如下图所示，它是按照行优先的顺序进行存储的。

　　

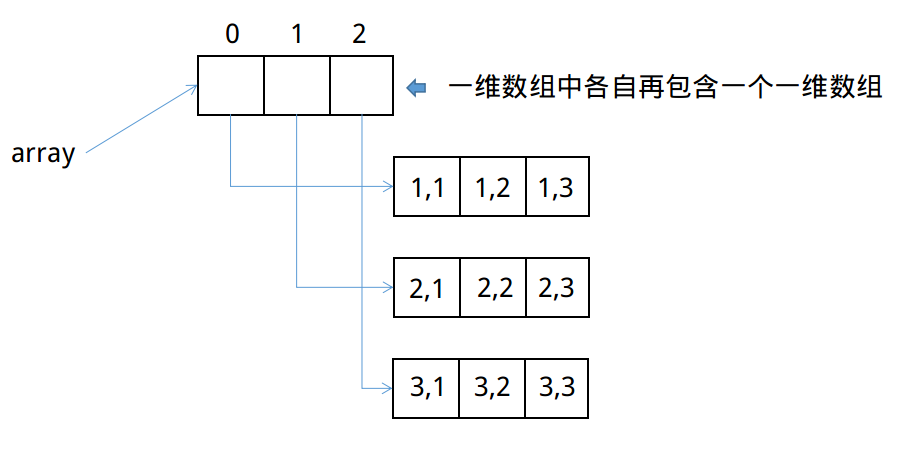
　　在编写矩阵计算的程序时，应当尽量避免跳跃访问矩阵中的元素——《算法笔记》。所以如果我们运算顺序是按照列来运算的话，此时Java定义的二维数组就会对元素进行跳跃访问。不妨利用一维数组按照自定义的行优先或者列优先来存储矩阵数据，这样对于列运算也有应对策略。

　　举个例子：

　　根据矩阵乘法的定义，A显然不能与X直接相乘，将A作转置得到：

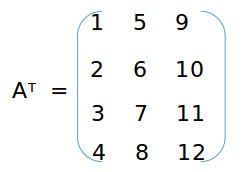
　　A与X相乘=>X·A^T：

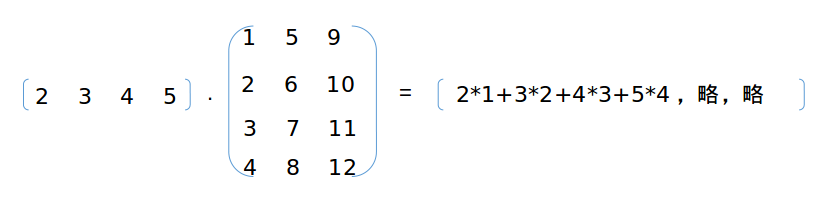
　　综上，A与X相乘可推出：

 

　　矩阵与向量相乘有两种实现方式（参照《算法笔记》）：

　　第一种：

for j ∈ {1, 2, 3, …, n} do
    bj ← 0
end for
for i ∈ {1, 2, 3, …, m} do
    for j ∈ {1, 2, 3, …, n} do
        bj ← bj + aij·xj
    end for
end for

　　显然利用这种方式计算矩阵与向量的乘积时，按行优先存储的矩阵速度更快。

　　第二种：

for j ∈ {1, 2, 3, …, n} do
    bj ← 0
    for i ∈ {1, 2, 3, …, m} do
        bj ← bj + aij·xj
    end for
end for

　　显然利用这种方式计算矩阵与向量的成绩时，按列优先存储的矩阵速度更快。