sf-1 算法

算法基础

算法

算法（Algorithm）：一个计算过程，解决问题的方法

DNiklaus Wirth:“程序=数据结构+算法”

 

时间复杂度

时间复杂度：用来评估算法运行效率的一个式子

 

 

 

 

时间复杂度-小结

时间复杂度是用来估计算法运行时间的一个式子（单位）。
一般来说，时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度（按效率排序）

O（1）< O（logn）< O（n）< O（nlogn）< O（n²）< O（n²logn）< O（n³）
复杂问题的时间复杂度
O（n！）O（2ⁿ）O（nⁿ）..

 

如何简单快速地判断算法复杂度

快速判断算法复杂度（适用于绝大多数简单情况）：
　　确定问题规模n
　　循环减半过程→logn
　　k层关于n的循环→n^k
复杂情况：根据算法执行过程判断

空间复杂度

空间复杂度：用来评估算法内存占用大小的式子
空间复杂度的表示方式与时间复杂度完全一样
　　算法使用了几个变量：O（1）
　　算法使用了长度为n的一维列表：O（n）
　　算法使用了m行n列的二维列表：O（mn）
“空间换时间”

 

递归的两个特点：
　　调用自身
　　结束条件

 

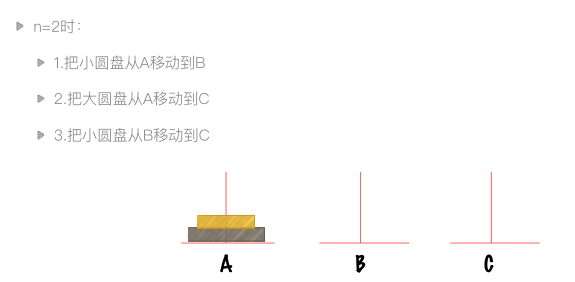
 递归实例：汉诺塔问题

大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摆着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
64根柱子移动完毕之日，就是世界毁灭之时。

 

 

汉诺塔移动次数的递推式：h(x)=2h(x-1)+1
h(64)=18446744073709551615
假设婆罗门每秒钟搬一个盘子，则总共需要5800亿年！

def hanoi(n, a, b, c):
    if n > 0:  # 盘子大于0才执行
        hanoi(n - 1, a, c, b)  # 将n-1个盘 从a经过c移动到 b
        print("moving pan from %s to %s" % (a, c))  # 将第n个盘移动到c
        hanoi(n - 1, b, a, c)  # 将n-1 个盘 从b 经过a 移动到c

hanoi(3, 'A', 'B', 'C')

# 将n-1个盘（除了底层的第n个盘）看成一个整体，

"""
move pan from A to C
move pan from A to B
move pan from C to B
move pan from A to C
move pan from B to A
move pan from B to C
move pan from A to C
"""

 

列表查找

查找
查找：在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程。
列表查找（线性表查找）：从列表中查找指定元素

输入：列表、待查找元素
输出：元素下标（未找到元素时一般返回None或-1）

内置列表查找函数：index（）

 

顺序查找（Linear Search）

顺序查找：也叫线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。
时间复杂度：O（n）

 

 

 

二分查找（Binary Searh）

二分查找：又叫折半查找，从有序列表的初始候选区li[0：n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

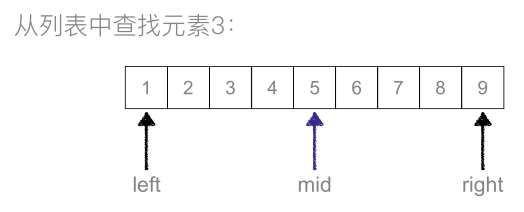
def binary(data_list, value):
    low = 0
    high = len(data_list) - 1
    while low <= high:
        mid = (low + high) // 2          # 折半
        if data_list[mid] == value:
            return mid
        elif data_list[mid] > value:
            high = mid - 1
        else:
            low = mid + 1


data_list = [1, 2, 3, 4, 5, 6, 7, 8, 9]
value = 5
index = binary(data_list, value)
print("index in data_list:%s ,search value test:%s "%(index,data_list[index]))

"""
index in data_list:4 ,search value test:5 
"""