4 中心差分和迎风差分
背景
在《3. 有限体积法:推导方程》等之前的课程中,我们已经讨论了如下方程,一个是稳态对流-扩散方程:
\[\begin{equation}
\nabla\cdot(\rho\boldsymbol{u}\phi)=\nabla\cdot(\Gamma\nabla\phi)^{+}S_{\phi}
\end{equation}
\]
它关于一个控制体积的积分形式为:
\[\begin{equation}
\int_An\cdot(\rho u\phi)dA=\int_An\cdot[\Gamma\nabla\phi]dA+\int_{CV}s_\phi dA
\end{equation}
\]
在一个控制体积中的通量平衡:左侧给出净对流通量,右侧给出净扩散通量,控制体积内就涉及物理量\(\phi\)的产生或毁灭了。
关于对流项的离散,有一个问题,是关于在一个控制体积的表面,输运的物理量\(\phi\),以及其穿过边界1的对流通量的计算。
稳态一维对流与扩散
回顾一下《1:数值方法A》中的一维热传导方程。我们在这里考虑相同形式的,在给定的一维流场u当中,某物理量\(\phi\)的稳态对流和扩散:
\[\begin{equation}
\frac{d}{dx}(\rho u\phi)=\frac{d}{dx}{\left(\mathrm{Г}\frac{d\phi}{dx}\right)}
\end{equation}
\]
注意:这里\(\Gamma\)不是空气动力学中的环量,而是扩散系数。
注意,在这里,连续性要求:
\[\begin{equation}
\frac{d}{dx}(\rho u)=0
\end{equation}
\]
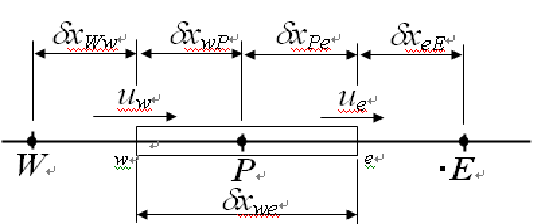
对上述公式3和4关于控制体积(如图,以w为左边界、e为右边界,流向从左向右)积分:
\[\begin{equation}
(\rho uA\phi)_e-(\rho uA\phi)_w=\left(\Gamma A\frac{\partial\phi}{\partial x}\right)_e-\left(\Gamma A\frac{\partial\phi}{\partial x}\right)_w
\end{equation}
\]
\[\begin{equation}
(\rho uA)_e-(\rho uA)_w=0
\end{equation}
\]
定义两个变量F和D,分别表示单位面积的对流质量通量、表面的扩散导热系数:
\[\begin{equation}
\begin{aligned}
F&=\rho u \\
D&=\frac{\Gamma}{\delta x}
\end{aligned}
\end{equation}
\]
这样,对该控制体积的西侧和东侧(左西右东),有:
\[\begin{equation}
\begin{aligned}
F_{w}&=(\rho u)_{w}A_{w}\\
D_{w}&=A_{w}\frac{\Gamma_{w}}{\delta x_{WP}}\\
F_{e}&=(\rho u)_{e}A_{e}\\
D_{e}&=A_{e}\frac{\Gamma_{e}}{\delta x_{PE}}\\
\end{aligned}
\end{equation}
\]
注意:没角标的D是单位面积的扩散导热系数,而有角标的是乘上了面积之后的扩散导热系数。
如果扩散系数\(\Gamma\)视为在每个控制体积内均匀分布,对于两个节点之间不等分间隔的扩散导热系数D可写作:
\[\begin{equation}
\frac{1}{D_w}=\frac{1}{D_W}+\frac{1}{D_P}=\frac{1}{A_W\frac{\Gamma_W}{\delta_{WW}}}+\frac{1}{A_P\frac{\Gamma_P}{\delta_{WP}}}
\end{equation}
\]
取倒数可得:
\[\begin{equation}
D_{w}=\frac{1}{\frac{1}{A_{W}\frac{\Gamma_{W}}{\delta_{WW}}}+\frac{1}{A_{P}\frac{\Gamma_{P}}{\delta_{WP}}}}=A_{w}\frac{1}{\left(\frac{\delta_{WW}}{\Gamma_{W}}+\frac{\delta_{WP}}{\Gamma_{P}}\right)}
\end{equation}
\]
这里我们回看上面的图,认为\(A_W=A_P=A_w\)(注意大小写)。
这样,我们可以得到当前控制体积左侧边界和右侧边界的扩散导热系数为:
\[\begin{equation}
D_w=A_w\left[\frac{\delta x_{Ww}}{\Gamma_W}+\frac{\delta x_{WP}}{\Gamma_P}\right]^{-1}\quad D_e=A_e\left[\frac{\delta x_{Pe}}{\Gamma_P}+\frac{\delta x_{eE}}{\Gamma_E}\right]^{-1}
\end{equation}
\]
我们回到公式5和6,即稳态对流-扩散方程和连续性方程,代入上述参数,有:
\[\begin{equation}
F_e\phi_e-F_w\phi_w=D_e(\phi_E-\phi_P)-D_w(\phi_P-\phi_W)
\end{equation}
\]
\[\begin{equation}
F_e-F_w=0
\end{equation}
\]
为求解方程12,需要计算在东/西侧的输运物理量\(\phi\)。
使用什么样的差分方法来求解或指定\(\phi_w\)和\(\phi_e\),是有限体积法的关键。
解析解和中心差分法
根据方程3,即微分形式的稳态对流-扩散方程描述,考虑一个通过对流和扩散方式,穿过一个一维域输运的物理量\(\phi\)。
定义边界条件为:在\(x=0\)处,\(\phi = \phi_0\);在\(x=L\)处,\(\phi = \phi_L\)。
求控制体积内任意位置\(x\in [0,~L]\)的解析解:
\[\begin{equation}
\frac{\phi-\phi_0}{\phi_L-\phi_0}=\frac{\exp\left(\frac{\rho ux}{\Gamma}\right)-1}{\exp\left(\frac{\rho uL}{\Gamma}\right)-1}=\frac{\exp\left(Pe\frac{x}{L}\right)-1}{\exp\left(Pe\right)-1}
\end{equation}
\]
这里引入了一个新概念:佩克数(Peclet number)\(Pe = \rho u\)。
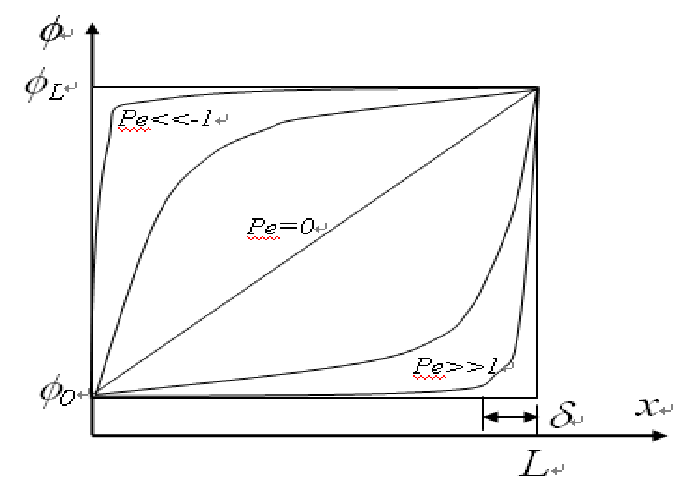
当佩克数\(Pe = 0\)时,在对流-扩散中,只考虑扩散效应。
如上图所示,此时物理量在控制体积内部的变化是线性的。
当\(Pe \gg 1\)时,解的表现类似边界层,上游(迎风)值在\(x=0\sim L\)之间占主要地位,而当x接近L时,内部物理量\(\phi\)迅速从\(\phi_0\)突变到\(\phi_L\),上图很好地展示了此时物理量突变的过程。
对于一个均匀网格(uniform grid),引入中心差分法(central diffusion),表面物理量\(\phi\)的值为:
\[\begin{equation}
\phi_e=\frac{\phi_P+\phi_E}{2}
\quad\phi_w=\frac{\phi_W+\phi_P}{2}
\end{equation}
\]
将上述结果回代到方程12,即稳态对流-扩散方程用对流质量通量F和扩散传导系数D表示:
\[\begin{equation}
\frac{F_e}{2}\left(\phi_P+\phi_E\right)-\frac{F_w}{2}\left(\phi_W+\phi_P\right)=D_e(\phi_E-\phi_P)-D_w(\phi_P-\phi_W)
\end{equation}
\]
重新排序,把物理量提出来,变成:
\[\begin{equation}
\begin{aligned}
&\underbrace{\left[\left(D_w+\frac{F_w}{2}\right)+\left(D_e-\frac{F_e}{2}\right)-(F_e-F_w)\right]}_{\boxed{a_P}}\phi_P\\
&=\underbrace{\left(D_w+\frac{F_w}{2}\right)}_{\boxed{a_W}}\phi_W+\underbrace{\left(D_e-\frac{F_e}{2}\right)}_{\boxed{a_E}}\phi_E
\end{aligned}
\end{equation}
\]
至此,我们把当前控制节点西侧节点的物理量\(\phi_W\)的系数\(a_W\)、东侧的物理量\(\phi_E\)的系数\(a_E\),获得了离散化对流-扩散方程的中心差分表达式。其基本形式为:
\[\begin{equation}
a_P\phi_P=a_W\phi_W+a_E\phi_E
\end{equation}
\]
其中:
- \(a_w = D_w + \frac{F_w}{2}\);
- \(a_E = D_e + \frac{F_e}{2}\);
- \(a_P = a_w + a_E + (F_e - F_w)\)。
注意到,对流质量通量F和佩克数Pe的表达式都是\(\rho u\),因此,如果Pe数是基于网格的特征长度尺度(grid characteristic length scale)得出的,我们可以把它称为网格佩克数,因此:
\[\begin{equation}
\begin{aligned}
\left[D_w\left(1+\frac{Pe}{2}\right)+D_e\left(1-\frac{Pe}{2}\right)-(F_e-F_w)\right]\phi_P\\=D_w\left(1+\frac{Pe}{2}\right)\phi_W+D_e\left(1-\frac{Pe}{2}\right)\phi_E
\end{aligned}
\end{equation}
\]
当佩克数小于2时,近似认为中心差分得到的结果和解析解相同。
当佩克数大于2时,系数\(a_E\)将会小于0,因此使用中心差分得到的解是不真实的。
故离散方程中的所有参数都应当大于0。
迎风差分
迎风差分(upwind differencing)或供体单元差分(donor cell differencing)法,在确定单元面的值时考虑流动方向,将单元面处的对流值\(\phi\)认为等于上游节点的值。
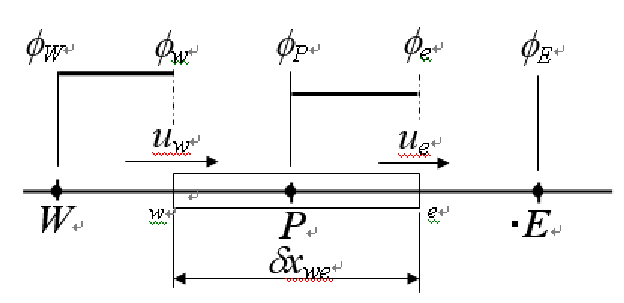
当流动方向从西向东时,认为西侧\(\phi_w = \phi_W\),东侧\(\phi_e = \phi_P\)。
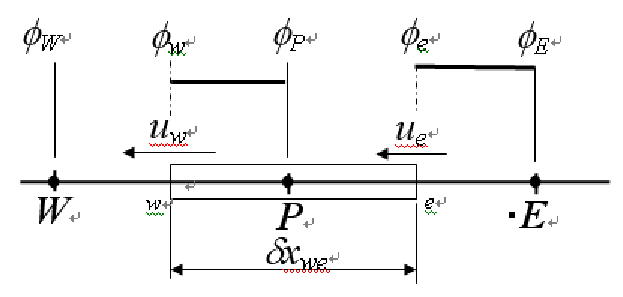
如果倒反天罡,让流动方向从东向西呢?
此时,我们认为,西侧表面的值变成当前节点中心的值,东侧表面的值变成东侧节点中心值,即\(\phi_w = \phi_P\),\(\phi_e = \phi_E\)。
我们用一种方便编程的方式,描述每个表面的对流通量:
\[\begin{equation}
\begin{aligned}
(\rho u\phi)_{e}&=F_{e}\phi_{e}=\phi_{P}max(F_{e},0)-\phi_{E}\max(-F_{e},0)\\
(\rho u\phi)_{w}&=F_{w}\phi_{w}=\phi_{W}max(F_{w},0)-\phi_{P}\max(-F_{w},0)
\end{aligned}
\end{equation}
\]
解释一下这组方程,以西侧表面的物理量\(\phi_w\)为例,考虑流动从西向东:
- \(\phi_w = \phi_W\),此时\(F_w\)为正,max(\(F_w,~0\))为\(F_w\),\(\phi_W\)项不为0;max(\(-F_w,~0\))为0,\(\phi_P\)项为0。
回代到方程12,即稳态对流-扩散方程用对流质量通量F和扩散传导系数D表示,可得:
\[\begin{equation}
\begin{aligned}
&\phi_P\max(F_e,0) - \phi_E\max(-F_e,0) \\
& - \phi_W\max(F_w,0) + \phi_P\max(-F_w,0) \\
& = D_e(\phi_E - \phi_P) - D_w(\phi_P - \phi_W)
\end{aligned}
\end{equation}
\]
对上述公式重新排列,有:
\[\begin{equation}
\begin{aligned}
&[D_w(1+max(Pe,0))+D_e(1+max(-Pe,0))+(F_e-F_w)]\phi_P\\
&=D_w(1+max(Pe,0))\phi_W+D_e(1+max(-Pe,0))\phi_E
\end{aligned}
\end{equation}
\]
我们把它用标准形式\(a_P\phi_P=a_W\phi_W+a_E\phi_E\)表示,其中:
- \(a_W = D_w[1 + max(Pe,~0)]\);
- \(a_E = D_e[1 + max(-Pe,~0)]\);
- \(a_P = a_W + a_E + (F_e - F_w)\)。
总结
中心差分和迎风差分的本质,都是构建形如\(a_P\phi_P=a_W\phi_W+a_E\phi_E\)的方程,其中\(a_P = a_W + a_E + (F_e - F_w)\)。
但对于参数\(a_W\)和\(a_E\)(分别描述西侧网格中心节点,和东侧网格中心节点),见下表。
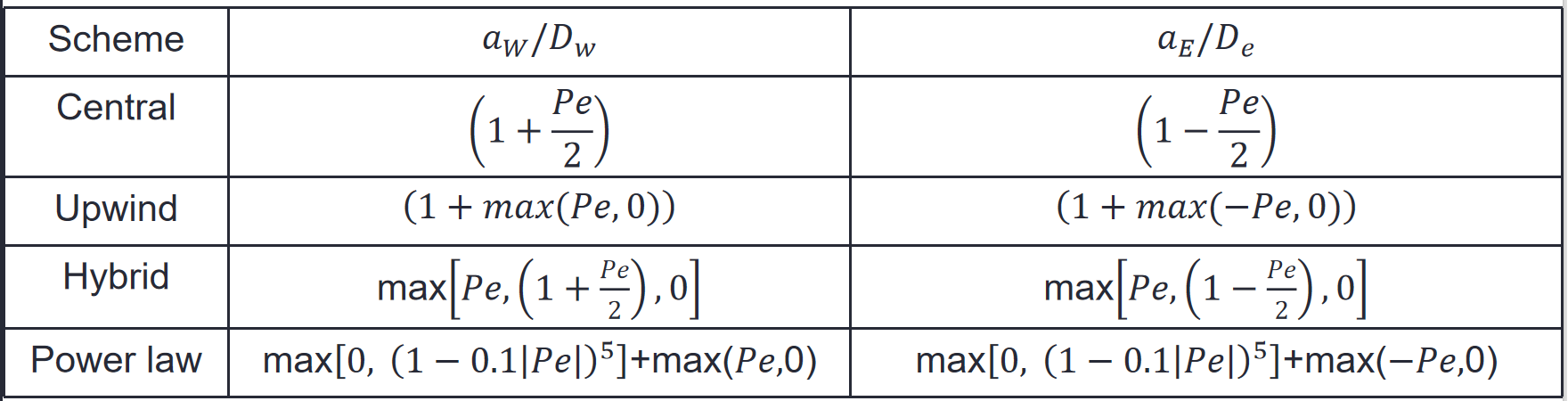









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· Qt个人项目总结 —— MySQL数据库查询与断言