X.3 一维梁
X.3 一维梁
一维连续系统
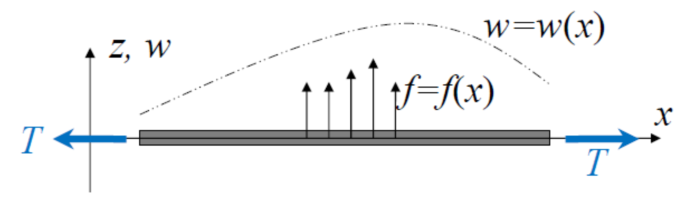
本图中，w表示梁在z方向的挠度（deflection，或位移），f表示每单元长度受到的横向力（transverse force），T表示弦（string）受到的张力。
对于一维张紧弦，其控制方程为：
\[\begin{equation}
T\frac{d^2w}{dx^2}+f\begin{pmatrix}x\end{pmatrix}=0
\end{equation}
\]
该方程的推导过程如下。
其边界条件为：当\(x=x_L\)（左端）或\(x=x_R\)（右端）时，
- 固定端（dirichlet boundary condition）：\(w=0\)，表示弦的该端点被固定住，不允许有任何位移；
- 自由端（neumann boundary condition）：\(\frac{dw}{dx}=0\)，表示弦的该端点可以自由移动，但其斜率必须为零。
在物理上，这表示弦在该端点处是水平的，尽管可以自由地上下移动，但不会发生扭曲或倾斜。
二维情形下（以一个二维薄膜为例）：
\[\begin{equation}
\frac{\partial^2w}{\partial x^2}+\frac{\partial^2w}{\partial y^2}=f\begin{pmatrix}x,y\end{pmatrix}
\end{equation}
\]
回到一维问题，我们对该方程求解的结果是\(w=w(x)\)，即弦在z方向（有时称为横向）位移沿着x方向的分布。
弱形式（weak form）
一维控制方程是二阶常微分方程，是一个强形式。
强形式直接通过物理定律给出系统的微分方程及其边界条件，多为高阶微分方程，对函数光滑性要求较高。
为减轻计算复杂度，把强形式与一个测试函数相乘，进行加权积分、分部积分，转化为弱形式。
这样的好处是降低了微分方程的阶数，允许解更不光滑，并为后续进行离散近似奠定基础。
对一维控制方程进行积分，可得：
\[\begin{equation}
\int_{x_L}^{x_R}\left(T\frac{d^2w}{dx^2}+f(x)\right)\varphi_j(x)dx=0
\end{equation}
\]
其中\(\varphi_j~(j = 1,~2,~...,~ \infin)\)是测试函数。
测试函数通常需要满足如下性质：
-
在定义域内有定义；
-
具有一定的光滑性，如至少可导一次；
-
满足边界条件；
-
线性无关，通常选取简单的函数形式，如：
- 多项式：\(\phi_j (x)=x^j\)
- 分段线性函数
- 正弦、余弦函数等
对上述方程进行分部积分，最终得到的弱形式为：
\[\begin{equation}
\int_{x_{L}}^{x_{R}}\left[T\frac{dw}{dx}\frac{d\varphi_{j}}{dx}-f(x)\varphi_{j}(x)\right]dx=0
\end{equation}
\]
有限元素法
受力公式与刚度矩阵推导
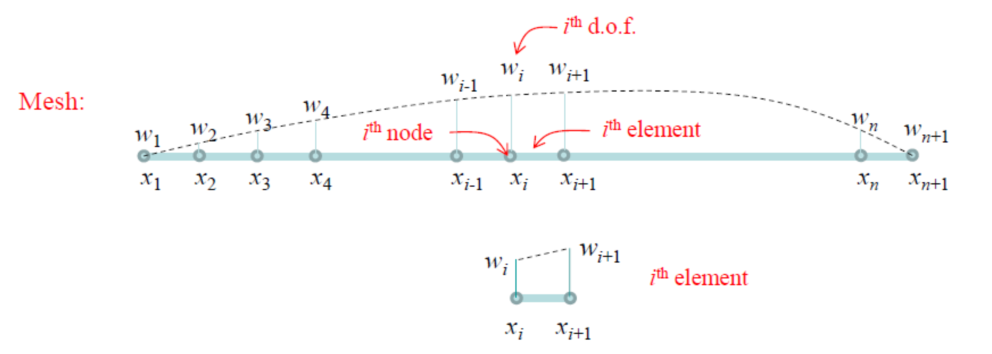
对于目前这个一维弦，我们将整个域离散（discretise）为有限个数的元素。
如上图所示，考虑一段微元，设已知左右边界处的位移值。
为了解该微元内任意位置的位移，使用线性插值（interpolation），即将有限元单元内的场表示为节点值的线性组合：
\[\begin{equation}
w(x)=w_i+\frac{w_{i+1}-w_i}{x_{i+1}-x_i}(x-x_i)
\end{equation}
\]
对上式进一步变形，可得：
\[\begin{equation}
\begin{aligned}
w(x)&=\frac{x_{i+1}-x}{x_{i+1}-x_{i}}w_{i}+\frac{x-x_{i}}{x_{i+1}-x_{i}}w_{i+1}\\&=N_{i}\left(x\right)w_{i}+N_{i+1}\left(x\right)w_{i+1}
\end{aligned}
\end{equation}
\]
相当于这里的\(N_i\)和\(N_{i+1}\)用于表示斜率。
下一步，参照公式4（弱形式一维张紧弦控制公式），稍微改一下范围（左端变成\(x_1\)，右端变成\(x_{n+1}\)）：
\[\begin{equation}
\begin{aligned}
&\int_{x_1}^{x_{n+1}}\left(T\frac{dw}{dx}\frac{d\varphi_j}{dx}-f(x)\varphi_j(x)\right)dx\\&=\sum_{i=1}^{n}\int_{x_i}^{x_{i+1}}\left(T\frac{dw}{dx}\frac{d\varphi_j}{dx}-f(x)\varphi_j(x)\right)dx=0
\end{aligned}
\end{equation}
\]
回到式6，把有限元单元内的位移场转化为矩阵形式：
\[\begin{equation}
w(x)=\begin{bmatrix}N_i\begin{pmatrix}x\end{pmatrix}&N_{i+1}\begin{pmatrix}x\end{pmatrix}\end{bmatrix}\begin{Bmatrix}w_i\\w_{i+1}\end{Bmatrix}=\begin{bmatrix}S\end{bmatrix}\begin{Bmatrix}\Delta\end{Bmatrix}^e
\end{equation}
\]
对位移关于x坐标求导，并以矩阵形式表示：
\[\begin{equation}
\begin{aligned}
\frac{dw}{dx}&=N_i^{\prime}\left(x\right)w_i+N_{i+1}^{\prime}\left(x\right)w_{i+1}\\&=\begin{bmatrix}N_i^{\prime}\left(x\right)&N_{i+1}^{\prime}\left(x\right)\end{bmatrix}\left\{\begin{array}{c}w_i\\w_{i+1}\end{array}\right\}\\&=\begin{bmatrix}B\end{bmatrix}\{\Delta\}^e
\end{aligned}
\end{equation}
\]
这里的\([B]\)是应变矩阵（kinematic matrix）。
下一步，我们把位移\(w(x)\)用函数\(f(x)\)表示，变换一下方程8：
\[\begin{equation}
f(x)=N_{i}\left(x\right)f_{i}+N_{i+1}\left(x\right)f_{i+1}=[S]\begin{Bmatrix}{f_{i}}\\{f_{i+1}}\end{Bmatrix}
\end{equation}
\]
其中，\(\begin{Bmatrix}f_i\\f_{i+1}\end{Bmatrix}=\begin{Bmatrix}f(x_i)\\f(x_{i+1})\end{Bmatrix}\)。
这里的\(N\)正式名称叫形函数（shape function），是决定每个节点值对插值函数贡献程度的权重函数。
其性质如下：
- 每个形函数与一个特定的节点相关联；
- 对于同一类型的单元，所有节点的形函数具有相同形式；
- 可以使用无量纲坐标表示形函数。
其公式如下：
\[\begin{equation}
\begin{aligned}
&N_{i}\left(x\right)=\frac{x_{i+1}-x}{x_{i+1}-x_{i}}\quad N_{i+1}\left(x\right)=\frac{x-x_{i}}{x_{i+1}-x_{i}}\\&N_{i}^{\prime}\left(x\right)=-\frac{1}{x_{i+1}-x_{i}}\quad N_{i+1}^{\prime}\left(x\right)=\frac{1}{x_{i+1}-x_{i}}
\end{aligned}
\end{equation}
\]
考虑我们之前讨论的测试函数，令\(\phi_j(x)=N_j(x)\)，则对于第\(i\)个元素，有：
\[\begin{equation}
\begin{aligned}
&\int_{x_{i}}^{x_{i+1}}\left(T\frac{d\varphi_{j}}{dx}\frac{dw}{dx}-f(x)\varphi_{j}(x)\right)dx\\&=\int_{x_{i}}^{x_{i+1}}\left(\frac{dN_{j}}{dx}T\frac{dw}{dx}-N_{j}(x)f(x)\right)dx
\end{aligned}
\end{equation}
\]
这里对于第\(i\)个元素，\(j=i,~i+1\)。
那么，结合式9，把\(\frac{dw}{dx}\)表示为\([B]\{\Delta\}\)（应变矩阵*位移），同时把\(\frac{dN_j}{dx}\)换成\(N'\)，式12变成：
\[\begin{equation}
\begin{aligned}&\int_{x_{i}}^{x_{i+1}}\left(N_{i}^{\prime}T\left[B\right]\left\{\Delta\right\}^{e}-N_{i}f(x)\right)dx\\&\int_{x_{i}}^{x_{i+1}}\left(N_{i+1}^{\prime}T\left[B\right]\left\{\Delta\right\}^{e}-N_{i+1}f(x)\right)dx\end{aligned}
\end{equation}
\]
将上述两式综合，得：
\[\begin{equation}
\int_{x_i}^{x_{i+1}}\left(\begin{Bmatrix}N_i^{\prime}\\N_{i+1}^{\prime}\end{Bmatrix}T\left[B\right]\left\{\Delta\right\}^e-\begin{Bmatrix}N_i\\N_{i+1}\end{Bmatrix}f(x)\right)dx
\end{equation}
\]
其中：
\[\begin{equation}
\begin{aligned} &\begin{bmatrix}B\end{bmatrix}=\begin{bmatrix}N_i^{\prime}(x)&N_{i+1}^{\prime}(x)\end{bmatrix}\quad\\&\begin{bmatrix}B\end{bmatrix}^T=\begin{Bmatrix}N_i^{\prime}\\N_{i+1}^{\prime}\end{Bmatrix}
\end{aligned}
\end{equation}
\]
接下来，我们可以把式14描述成如下形式：
\[\begin{equation}
\begin{bmatrix}K\end{bmatrix}^e\begin{Bmatrix}\Delta\end{Bmatrix}^e-\begin{Bmatrix}F\end{Bmatrix}^e\quad\mathrm{or}\quad\begin{bmatrix}K\end{bmatrix}^{(i)}\begin{Bmatrix}\Delta\end{Bmatrix}^{(i)}-\begin{Bmatrix}F\end{Bmatrix}^{(i)}
\end{equation}
\]
其中：
\[\begin{equation}
\begin{aligned}&\left[K\right]^{e}=\int_{x_{i}}^{x_{i+1}}\left[B\right]^{T}T\left[B\right]dx\\
&\left\{F\right\}^{e}=\int_{x_{i}}^{x_{i+1}}\begin{Bmatrix}N_{i}\\N_{i+1}\end{Bmatrix}f(x)dx=\left(\int_{x_{i}}^{x_{i+1}}\left[S\right]^{T}\left[S\right]dx\right)\begin{Bmatrix}f_{i}\\f_{i+1}\end{Bmatrix}\end{aligned}
\end{equation}
\]
关于这里的\(S\)，回顾式8，\([S]=\begin{bmatrix}N_i\begin{pmatrix}x\end{pmatrix}&N_{i+1}\begin{pmatrix}x\end{pmatrix}\end{bmatrix}\)，转置一下就变成竖的了。
关于这里\(f(x)\)的变形，回顾式10，\(f(x)=[S]\begin{Bmatrix}{f_{i}}\\{f_{i+1}}\end{Bmatrix}\)。
对式17中的K，我们做进一步变形：
\[\begin{equation}
\left[K^{e}\right]=\int_{x_{i}}^{x_{i+1}}\left[B\right]^{T}T\left[B\right]dx=\int_{x_{i}}^{x_{i+1}}\begin{Bmatrix}{N_{i}^{\prime}}\\{N_{i+1}^{\prime}}\end{Bmatrix}T\begin{bmatrix}{N_{i}^{\prime}}&{N_{i+1}^{\prime}}\end{bmatrix}dx
\end{equation}
\]
而对式17中的F，我们也可以做变形：
\[\begin{equation}
\begin{aligned}
&\left.\left\{F\right\}^{e}=\left\{\begin{array}{c}{F_{i}}\\{F_{i+1}}\end{array}\right.\right\}=\begin{pmatrix}{\int_{x_{i}}^{x_{i+1}}\left[S\right]^{T}\left[S\right]dx}\end{pmatrix}\begin{Bmatrix}{f_{i}}\\{f_{i+1}}\end{Bmatrix}\\&=\begin{pmatrix}{\int_{x_{i}}^{x_{i+1}}\begin{Bmatrix}{N_{i}}\\{N_{i+1}}\end{Bmatrix}\begin{bmatrix}{N_{i}}&{N_{i+1}}\end{bmatrix}dx}\end{pmatrix}\begin{Bmatrix}{f_{i}}\\{f_{i+1}}\end{Bmatrix}
\end{aligned}
\end{equation}
\]
接着，我们对形函数\(N\)进行处理，回顾式11。
针对K公式，进行如下操作：
\[\begin{equation}
\begin{aligned}
&\left.\left\{\begin{array}{c}N_i^{\prime}\\N_{i+1}^{\prime}\end{array}\right.\right\}T\left[N_i^{\prime}\quad N_{i+1}^{\prime}\right]\\&=\begin{Bmatrix}-\frac{1}{x_{i+1}-x_i}\\\frac{1}{x_{i+1}-x_i}\end{Bmatrix}T\left[-\frac{1}{x_{i+1}-x_i}\quad\frac{1}{x_{i+1}-x_i}\right]\\&=\frac{T}{\left(x_{i+1}-x_i\right)^2}\begin{Bmatrix}-1\\1\end{Bmatrix}\left[-1\quad1\right]\\
&= \frac{T}{\left( x_{i+1} - x_i \right)^2}
\begin{bmatrix}
1 & -1 \\
-1 & 1
\end{bmatrix}
\end{aligned}
\end{equation}
\]
回代：
\[\begin{equation}
[K^e]=\frac{T}{x_{i+1}-x_{i}}\begin{bmatrix}1&-1\\-1&1\end{bmatrix}
\end{equation}
\]
下一步，对F公式进行处理：
\[\begin{equation}
\begin{aligned}
&\left.\left\{\begin{array}{c}N_i\\N_{i+1}\end{array}\right.\right\}
\left[N_i \quad N_{i+1}\right] \\
&= \begin{Bmatrix}
\frac{x_{i+1} - x}{x_{i+1} - x_i} \\
\frac{x - x_i}{x_{i+1} - x_i}
\end{Bmatrix}
\begin{bmatrix}
\frac{x_{i+1} - x}{x_{i+1} - x_i} & \frac{x - x_i}{x_{i+1} - x_i}
\end{bmatrix} \\
&= \frac{1}{\left( x_{i+1} - x_i \right)^2}
\begin{bmatrix}
\left( x_{i+1} - x \right)^2 & \left( x_{i+1} - x \right)\left( x - x_i \right) \\
\left( x_{i+1} - x \right)\left( x - x_i \right) & \left( x - x_i \right)^2
\end{bmatrix}
\end{aligned}
\end{equation}
\]
首先计算矩阵中元素分别积分的结果：
\[\begin{equation}
\begin{aligned}
&\int_{x_{i}}^{x_{i+1}} \left(x_{i+1} - x\right)^{2} \, dx = -\frac{1}{3} \left(x_{i+1} - x\right)^{3} \bigg|_{x_{i}}^{x_{i+1}} = \frac{1}{3} \left(x_{i+1} - x_{i}\right)^{3} \\
&\int_{x_{i}}^{x_{i+1}} \left(x_{i+1} - x\right) \left(x - x_{i}\right) \, dx
\\&= -\frac{1}{2} \left[ \left(x_{i+1} - x\right)^{2} \left(x - x_{i}\right) \right] \bigg|_{x_{i}}^{x_{i+1}} + \frac{1}{2} \int_{x_{i}}^{x_{i+1}} \left(x_{i+1} - x\right)^{2} \, dx
\\&= \frac{1}{6} \left(x_{i+1} - x_{i}\right)^{3} \\
&\int_{x_{i}}^{x_{i+1}} \left(x - x_{i}\right)^{2} \, dx = \frac{1}{3} \left(x - x_{i}\right)^{3} \bigg|_{x_{i}}^{x_{i+1}} = \frac{1}{3} \left(x_{i+1} - x_{i}\right)^{3}
\end{aligned}
\end{equation}
\]
然后再回代到F，公式19：
\[\begin{equation}
\begin{aligned}
&\{F^e\}\left.=\frac{x_{i+1}-x_{i}}{6}\left[\begin{array}{cc}{2}&{1}\\{1}&{2}\end{array}\right.\right]\begin{Bmatrix}{f_{i}}\\{f_{i+1}}\end{Bmatrix}\\&=\frac{x_{i+1}-x_{i}}{6}\begin{Bmatrix}{2f_{i}+f_{i+1}}\\{f_{i}+2f_{i+1}}\end{Bmatrix}
\end{aligned}
\end{equation}
\]
我们回顾一下整个推导过程：
\[\begin{equation}
\begin{aligned}&\int_{x_{1}}^{x_{n+1}}\left(T\frac{dw}{dx}\frac{d\varphi_{j}}{dx}-f(x)\varphi_{j}(x)\right)dx\\&=\sum_{i=1}^{n}\int_{x_{i}}^{x_{i+1}}\left(T\frac{dw}{dx}\frac{d\varphi_{j}}{dx}-f(x)\varphi_{j}(x)\right)dx\\&=\sum_{i=1}^{n}\left(\left[K\right]^{(i)}\left\{\Delta\right\}^{(i)}-\left\{F\right\}^{(i)}\right)\\&=\left[K\right]\left\{\Delta\right\}-\left\{F\right\}=0\end{aligned}
\end{equation}
\]
对于第i个元素：
\[\begin{equation}
\begin{aligned}
&\left[ K \right]^{(i)} \left\{ \Delta \right\}^{(i)} - \left\{ F \right\}^{(i)} \\
&=
\begin{bmatrix}
\frac{T}{x_{i+1} - x_{i}} & -\frac{T}{x_{i+1} - x_{i}} \\
-\frac{T}{x_{i+1} - x_{i}} & \frac{T}{x_{i+1} - x_{i}}
\end{bmatrix}
\begin{Bmatrix}
w_i \\
w_{i+1}
\end{Bmatrix}
-
\begin{Bmatrix}
\frac{1}{6} \big( 2f_i + f_{i+1} \big) \big( x_{i+1} - x_i \big) \\
\frac{1}{6} \big( f_i + 2f_{i+1} \big) \big( x_{i+1} - x_i \big)
\end{Bmatrix}
\end{aligned}
\end{equation}
\]
矩阵组装
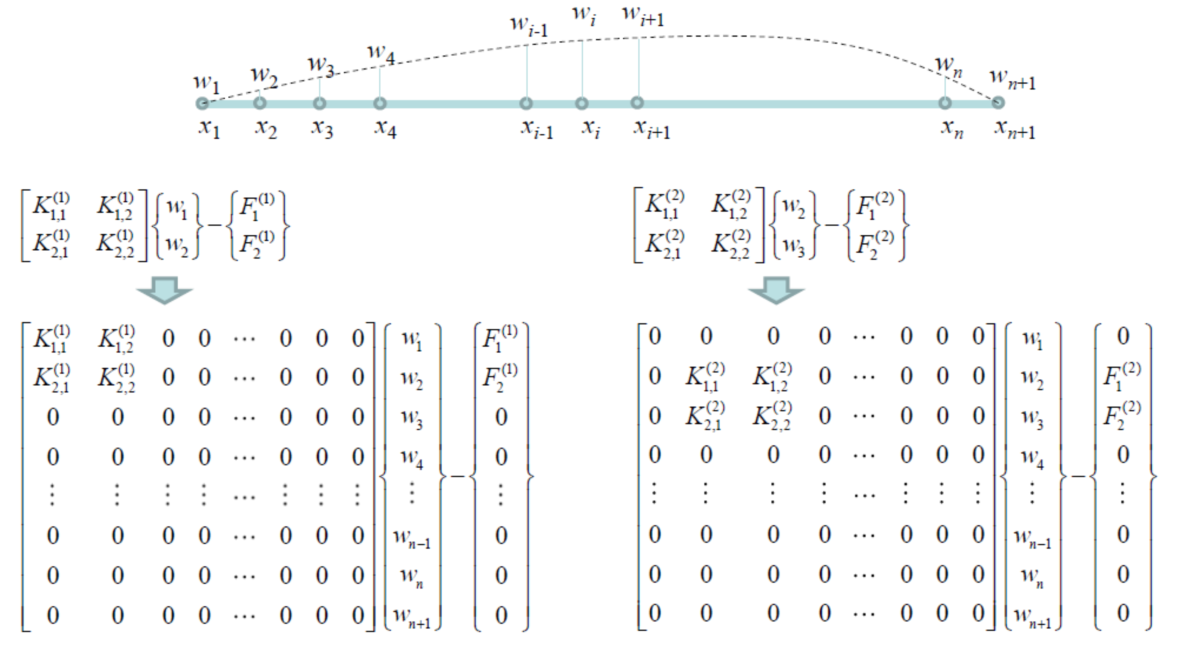
如图所示，我们把关于每个微元的公式，按顺序摆放在总的矩阵当中。
最后得到结果如下：
接下来考虑一种特殊情况：设弦的全长为L，单个元素长为\(x_{i+1}-x_i=\frac{L}{n}\)，弦受到横向匀布载荷\(f_i=f_{i+1}=f\)，此时刚度方程变成：
\[\begin{equation}
\begin{bmatrix}K\end{bmatrix}^{(i)}\begin{Bmatrix}\Delta\end{Bmatrix}^{(i)}-\begin{Bmatrix}F\end{Bmatrix}^{(i)}=\frac{nT}{L}\begin{bmatrix}1&-1\\-1&1\end{bmatrix}\begin{Bmatrix}w_i\\w_{i+1}\end{Bmatrix}-\frac{Lf}{2n}\begin{Bmatrix}1\\1\end{Bmatrix}
\end{equation}
\]
讨论和求解
\[\begin{equation}
T\frac{d^2w}{dx^2}+f\left(x\right)=0\quad\leftrightarrow\quad\begin{bmatrix}K\end{bmatrix}\{\Delta\}=\begin{Bmatrix}F\end{Bmatrix}
\end{equation}
\]
我们把控制方程（一个微分方程）转化为了矩阵形式，这样更有利于计算机求解。
为了求解，我们还需要引入一组边界条件，如：
\[\begin{equation}
w|_{x=x_{L}}=w|_{x=x_{R}}=0\quad\leftrightarrow\quad w_{1}=w_{n+1}=0\quad\leftrightarrow\quad R_{1}\&R_{n+1}
\end{equation}
\]
这里的R代表reactions，即支座反力。
代入边界条件：
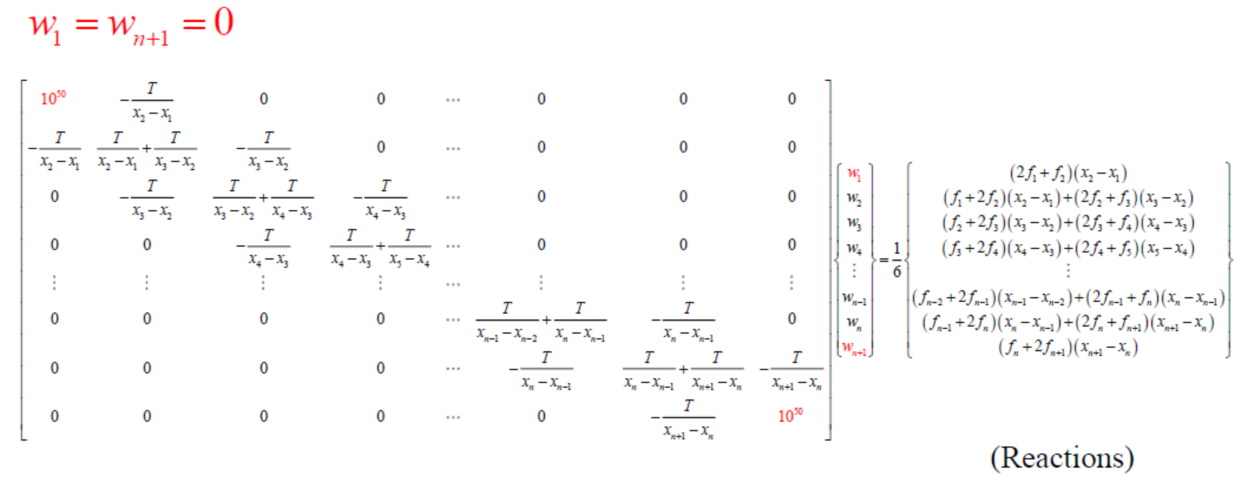
下面以一个具体的求解案例结束这一节。
