1-1 数值方法B
1-1 数值方法B
非稳态扩散方程
主体公式
该式左边为时间导数，表示某一点的能量随时间的变化；右边为空间变化，描述热在空间扩散的过程。
其边界条件为：\(T(x,~t=0)\)
其解决思路为：首先从t=0出发，准备初始条件（即上述边界条件）；
当\(t=1\Delta t\)时，对方程离散化，获取线性方程，并利用上述边界条件，得到的解为\(T(x,~t=1\Delta t\)；
对\(t=2\Delta t\)，新的初始条件为\(T(x,~t=1\Delta t)\)，同样进行离散化，并用新边界条件求解。
重复直到\(t=t_{final}\)，此时求出的解为\(T(x,~t=t_{final})\)。
对每一步求解，我们都需要求解一个新的线性系统[A][T]=[B]。
离散化
考虑无源项的公式：
进行时间和空间上的积分：
这里，\(T_P^0\)是t时刻点P处的温度，\(T_P^1\)是\(t+\Delta t\)时刻点P处的温度。
但这一步还不够，为得到温度随时间的变化，设温度\(T(t)\)在时刻t和\(t+\Delta t\)之间呈线性变化。
有如下公式：
其中，该式等号左边部分是在时间区间\([t,~\Delta t]\)内，对点P处温度进行积分，得到的是温度的累计效果；
右边部分是用点P处温度在时刻t和\(t+\Delta t\)的加权平均值，乘以时间步长\(\Delta t\)得到的近似值。
在右边部分中，f是时间离散化的权重系数：
- f=0：显式欧拉法/前向差分法，只使用当前时刻温度；
- f=1：隐式欧拉法/后向差分法，只使用下一时刻温度；
- f=0.5：中点法，对当前时刻和下一时刻的温度取平均值。
则一维非稳态热传导公式变为：
其中：
-
项\(\rho\)\(c_p\)\((T_{P}^1\)\(-T_P^0)\)\(\Delta x\)是储能项，表示控制节点P在时间段\(\Delta t\)内因为温度变化产生的能量变化，\(\rho c_p \Delta x\)表示节点P控制体积的总热容量；
-
项
\[f[\lambda_{e}\frac{T_{E}^{1}-T_{P}^{1}}{\delta x_{e}}-\lambda_{w}\frac{T_{P}^{1}-T_{W}^{1}}{\delta x_{w}}] \]表示基于未来时刻\(t+\Delta t\)的传导项。
其物理意义为：-热通量=热导率*温度梯度（即\(\lambda \frac{\Delta T}{\delta x}\)），表示热量从高温区流向低温区的速率。
其中，\(\lambda_{e}\frac{T_{E}^{1}-T_{P}^{1}}{\delta x_{e}}\)表示热量从节点E传导向节点P，\(-\lambda_{w}\frac{T_{P}^{1}-T_{W}^{1}}{\delta x_{w}}\)表示热量从节点P传导向节点W，这里的负号表示节点P损失热量。
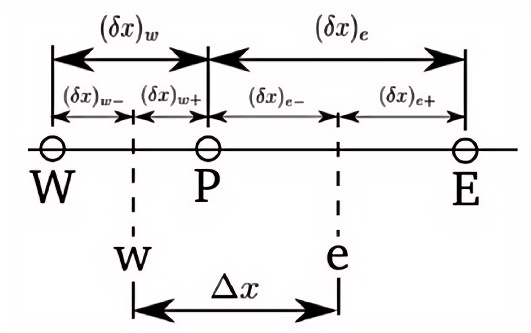
\(\delta x_e\)和\(\delta x_w\)是节点距离，它们决定了温度梯度的大小。
重新排列该方程，最终可得：
即下述线性方程：
其中，\(a_w=-f\frac{\lambda_w}{\delta x_w}\)，\(a_p=\rho c_p\frac{\Delta x}{\Delta t}+f(\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e})\)，\(a_e=-f\frac{\lambda_e}{\delta x_e}\)；
\(b=\rho c_p\frac{\Delta x}{\Delta t}T_P^0+(1-f)[\frac{\lambda_w}{\delta x_w}T_W^0+\frac{\lambda_e}{\delta x_e}T_E^0-(\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e})T_P^0]\)。
下面依次讨论三种不同的权重系数f下，方程的形式。
-
f=0：
\[\left(\rho c_p\frac{\Delta x}{\Delta t}\right)T_P=\frac{\lambda_w}{\delta x_w}T_W^0+\frac{\lambda_e}{\delta x_e}T_E^0+[\rho c_p\frac{\Delta x}{\Delta t}-\left(\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e}\right)]T_P^0 \]重新排列上述公式：
\[T_P+\left(\frac{\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e}}{\rho c_p\frac{\Delta x}{\Delta t}}-1\right)T_P^0=\frac{\frac{\lambda_w}{\delta x_w}T_W^0+\frac{\lambda_e}{\delta x_e}T_E^0}{\rho c_p\frac{\Delta x}{\Delta t}} \]对照\(a_W T_W+a_P T_P+a_E T_E=b\)，其系数如下：
\(a_P=\rho c_P \frac{\Delta x}{\Delta t}\)，\(a_E=a_W=0\)，
\(b=\frac{\lambda_w}{\delta x_w}T_W^0+\frac{\lambda_e}{\delta x_e}T_E^0-(\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e}-\rho c_p\frac{\Delta x}{\Delta t})T_P^0\)
为确保解的稳定性，当前节点当前时间的温度\(T_P^0\)的系数：
\(\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e}-\rho c_p\frac{\Delta x}{\Delta t}\)需要为负数，确保温度在每个时间步内无不合理增长。
该系数的意义为：如果系数为正，中心点的温度\(T_P\)会不受控地增长，使得解发散。可得：\(\Delta t<\frac{\rho c_p(\Delta x)^2}{2\lambda}\)时解稳定，此时\(\lambda_{w}=\lambda_{e},~\delta x_{w}=\delta x_{e}= \Delta x\)。
该方法为一阶精度，误差随着\(\Delta t\)线性增长；解耦，每个节点温度可以独立求解，但需严格控制\(\Delta t\)步长。 -
f=0.5：
\[\begin{aligned}&a_{P}=\rho c_{p} \frac{\Delta x}{\Delta t}+\frac{1}{2} ( \frac{\lambda_{w}}{\delta x_{w}}+\frac{\lambda_{e}}{\delta x_{e}}),\\&a_{E}=\frac{1}{2}\frac{\lambda_{e}}{\delta x_{e}},\\&a_{W}=-\frac{1}{2}\frac{\lambda_{w}}{\delta x_{w}},\\&b=\frac{1}{2}[ \frac{\lambda_{w}}{\delta x_{w}}T_{W}^{0}+\frac{\lambda_{e}}{\delta x_{e}}T_{E}^{0}-\left(\frac{\lambda_{w}}{\delta x_{w}}+\frac{\lambda_{e}}{\delta x_{e}}-2\rho c_{p}\frac{\Delta x}{\Delta t}\right)T_{P}^{0}]\end{aligned} \]解稳定的条件同f=0时。
该方法为二阶精度，\(\Delta t\)小的时候该方法最精确；非解耦，需要线性系统的解。 -
f=1：
\[\begin{aligned} &a_{P}=\rho c_{p}\frac{\Delta x}{\Delta t}+\frac{\lambda_{w}}{\delta x_{w}}+\frac{\lambda_{e}}{\delta x_{e}}, \\ &a_{E}=-\frac{\lambda_{e}}{\delta x_{e}}, \\ &a_{W}=-\frac{\lambda_{W}}{\delta x_{W}}, \\ &b=\rho c_p\frac{\Delta x}{\Delta t}T_P^0 \end{aligned} \]解稳定的条件：\(-\rho c_p\frac{\Delta x}{\Delta t}<0\)，对任何\(\Delta t\)都成立。
该方法为一阶精度，需要线性系统的解。
1-1.2 数值方法B 续
