1 数值方法A 续

1 数值方法A 续

下一步是用中心差分法近似\(\frac{dT}{dx}\)。

首先，对温度函数\(T(x)\)用泰勒展开，其中由于2阶以上项计算复杂、对结果影响小，故忽略。

假设在节点之间温度线性变化。

\[T(x)=T(x_i)+(x-x_i)\frac{dT}{dx}|_{x_i}+\frac{(x-x_i)^2}2\frac{d^2T}{dT^2}|_{x_i} \]

\[T(x_{P})=T(x_{e})-(\delta x)_{e^{-}}\cdot(-\frac{dT}{dx})|_{x_{e}}+\frac{(\delta x)_{e^{-}}^2}{2}\cdot(\frac{d^2T}{dT^2})|_{x_{e}} \]

\[T(x_E)=T(x_e)-(\delta x)_{e^+}\cdot (\frac{dT}{dx})|_{x_e}+\frac{(\delta x)_{e^+}^2}2 \cdot(\frac{d^2T}{dT^2})|_{x_e} \]

令e为P、E中点，则有\((\delta x)_{e^-}=(\delta x)_{e^+}=\frac{1}{2} (\delta x)_e\)，故：

\[\frac{dT}{dx}|_{x_e}=\frac{T(x_E)-T(x_P)}{(\delta x)_e} \]

回代入公式\((\lambda \frac{dT}{dx})_e-(\lambda \frac{dT}{dx})_w+\bar{S} \Delta x=0\)得：

\[(\lambda \frac{dT}{dx})_e=\lambda_e \cdot \frac{T_E-T_P}{(\delta x)_e} \]

\[(\lambda \frac{dT}{dx})_w=\lambda_w \cdot \frac{T_P-T_W}{(\delta x)_w} \]

另有：

\[\bar{S}=S_p \cdot T_P+S_c \]

把源项在控制体积内的均值\(\bar{S}\)线性化，其中\(S_P\)为线性系数（或斜率），\(S_c\)为常数项（或截距），二者均应当为常数。

那么，将我们得到的这三个公式组合起来，可以得到最终的线性化方程：

\[a_w T_w +a_p T_p+a_ET_E=b \]

其中，代表三个节点（当前控制节点左边一个、它本身、右边一个）的系数，以及右边一项b，分别是：

\[\quad a_W=-\frac{\lambda_w}{\delta x_w}\quad a_P=\frac{\lambda_w}{\delta x_w}+\frac{\lambda_e}{\delta x_e}-S_P\Delta x\quad a_E=-\frac{\lambda_e}{\delta x_e}\quad b=S_C\Delta x \]

注意，这个式子只能用于内部控制体积，不适用于边界节点。

对于边界条件：

• 已知温度：（\(T(x=0)=T_a\text,~T(x=L)=T_b\)）

  \[a_PT_P+a_ET_E=b,~a_P=1,~a_E=0,~b=T_a\\a_WT_W+a_PT_P=b,~a_P=1,~a_W=0,~b=T_b \]

• 已知温度随空间变化的导数，描述热流边界条件：
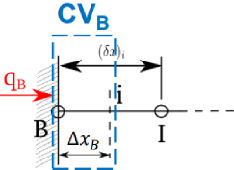  ​如图，定义热通量\(q_B=-\lambda \frac{dT}{dx}\)。

  \[(\lambda\frac{dT}{dx})_i-\left(\lambda\frac{dT}{dx}\right)_B+\bar{S}\Delta x_B=0 \]

  这里可以把\(-\left(\lambda\frac{dT}{dx}\right)_B\)这一项用\(q_B\)代替，于是可推出最后的线性化方程：

  \[a_PT_P+a_ET_E=b,~a_P=\frac{\lambda_e}{\delta x_e}-S_p\Delta x_B,~a_E=-\frac{\lambda_e}{\delta x_e},~\mathrm{b}=S_p\Delta x_B+q_B \]

​​

如图，最后得到了一个三对角矩阵。每个节点只影响其左侧一个和右侧一个节点。

求解线性方程组

判断解的稳定性

• 解是否有边界？

• 边界条件是否被遵守？

• 结果如何与理论解或实验数据比较，以验证数值解的正确性？

• 残差误差：

  \[R=\frac{|B-A\cdot T|}{|diag(A)\cdot T|}<tol \]

  其中，\(|B-A\cdot T|\)是残差，表示实际计算的结果\(A\cdot T\)与理论上应当得到的结果B之间的差；
  \(diag(A)\cdot T\)是矩阵A的对角线部分与T的乘积，用于对残差进行非量纲化，使得残差大小与系统的尺度保持一致。
  若R小于某个预设的容差tol，可认为解的精读是能接受的。

• 能量平衡：能量守恒必须在每个控制体中保持。有时源项\(\bar{S}=0\)，则控制体内的流入和流出热量\(q_w - q_e = 0\)。

• 网格收敛性：若网格细化，节点间距减半，误差应减少4倍。这种收敛特性在已知精确解时表现最好，通常通过对数-对数图（log-log plot）来评估收敛行为。

直接求解：高斯消元法

对如下矩阵：

\[\begin{bmatrix}a_{1,1}&a_{1,2}&a_{1,3}&...&a_{1,n}\\a_{2,1}&a_{2,2}&a_{2,3}&...&a_{2,n}\\\vdots&\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&a_{n,3}&...&a_{n,n}\end{bmatrix}\times\begin{bmatrix}T_1\\T_2\\\vdots\\T_n\end{bmatrix}=\begin{bmatrix}b_1\\b_2\\\vdots\\b_n\end{bmatrix} \]

1. 前向消元：将第i行减去第1行的某个倍数，使得\(a_{i,~1}=0\)，这样就能消去除了\(a_{1,~1}\)以外，矩阵A第1列的所有数；
   重复直到矩阵A变成上三角矩阵。
   ​​

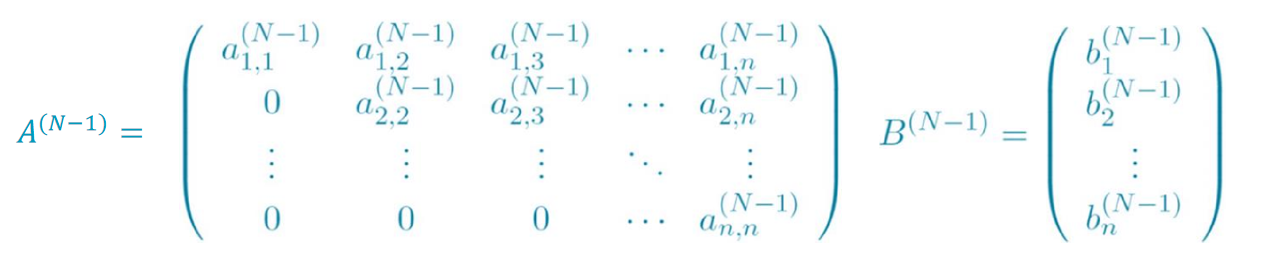
2. 回代：从最后一行开始，最后一行相当于解:

   \[a_{n,~n}^{(N-1)}\cdot T_n = b_n^{(N-1)} \]

   倒数第2行相当于解：

   \[a_{n-1,n-1}^{(N-1)}T_{n-1}+a_{n-1,n}^{(N-1)}T_n=b_{n-1}^{(N-1)} \]

   最后得到的通项公式为：

   \[T_i=\frac{b_i^{(N-1)}-\sum_{k=i+1}^na_{i,k}^{(N-1)}T_k}{a_{i,i}^{(N-1)}} \]

迭代求解：高斯-赛德尔法

通项公式：

\[T_i^{(m)}=\frac{b_i}{a_{i,i}}-\sum_{j=1}^{i-1}\frac{a_{i,j}}{a_{i,i}}T_j^{(m)}-\sum_{j=i+1}^n\frac{a_{i,j}}{a_{i,i}}T_j^{(m-1)}\\ =\frac{1}{a_{i,~i}}(b_i-\sum_{j=1}^{i-1}a_{i,j}T_j^{(m)}-\sum_{j=i+1}^na_{i,j}T_j^{(m-1)}) \]

其中：

• \(T_i^{(m)}\)表示第m次迭代中，第i个未知数的近似值；

• \(T_j^{(m)}\)表示第m次迭代中，第j个未知数近似值，j<i时，这些值在本次迭代中已更新；

• \(T_j^{(m-1)}\)表示第m次迭代中，第j个未知数近似值，j>i时，这些值在本次迭代中未更新；

• \(a_{i,~i}\)：矩阵A第i行i列元素；

• \(b_i\)：矩阵b第i行元素；

• \[\sum_{j=1}^{i-1}a_{i,j}T_j^{(m)} \]

  这一项对在第i行中，i之前的未知数项求和（已迭代）

• \[\sum_{j=i+1}^na_{i,j}T_j^{(m-1)} \]

  这一项对在第i行中，i之后的未知数项求和（未迭代）。

该法的物理意义为：通过\(b_i\)减掉加权求和，意为扣除已知部分，剩余未知数项的影响；除以\(a_{i,~i}\)则解出未知数。

‍