1 数值方法A

1 数值方法A

课堂笔记

基础

主要是针对N-S方程求解，有三种方法：有限体积、有限元、有限差分。

微分：

\[\underset{\Delta x \to 0}{lim} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\frac{dy}{dx} \]

​

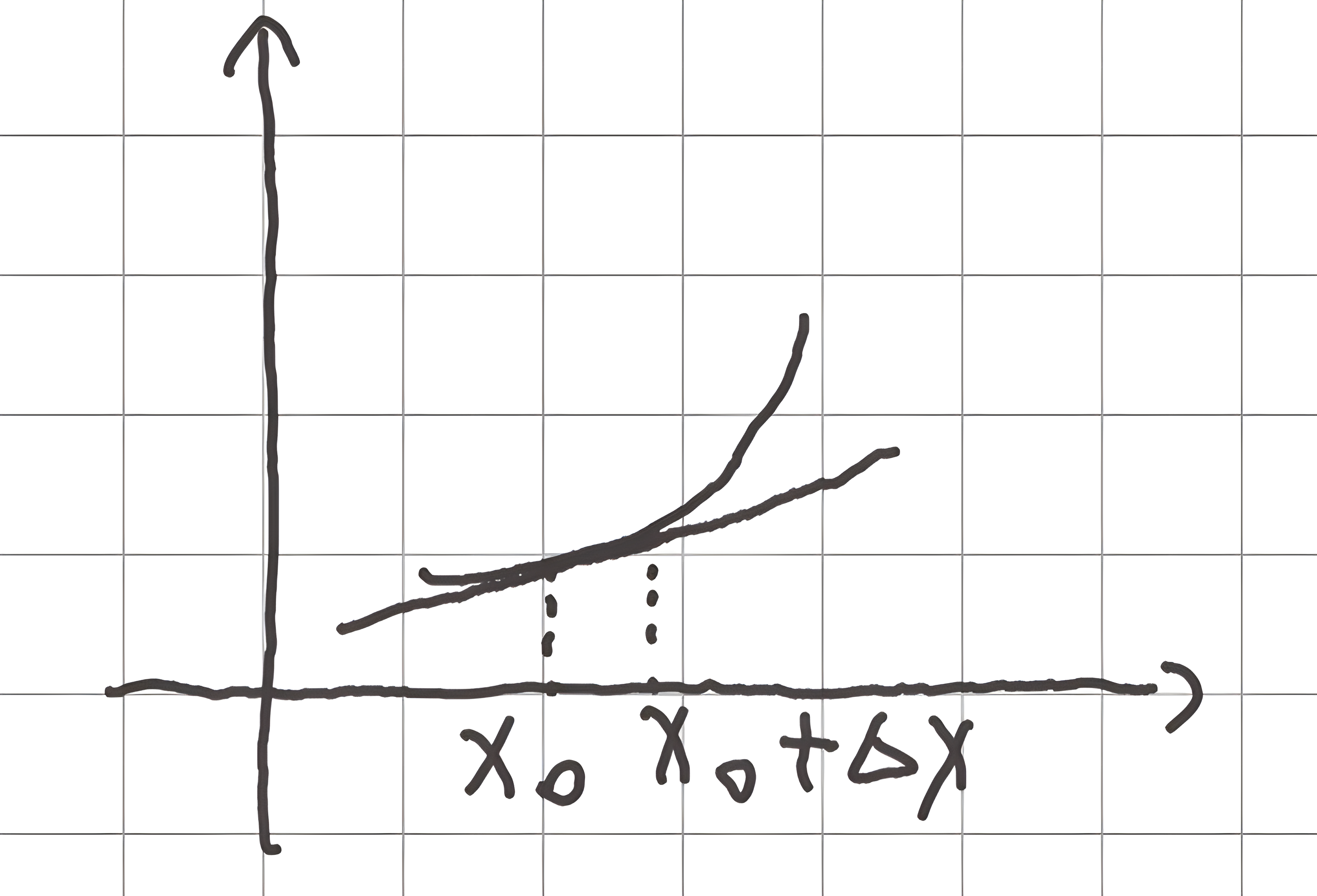
不同尺度下物质密度：分子尺度\(l_m\)<<连续体\(\eta\)<<地理尺度L（教室、地球...）

​​

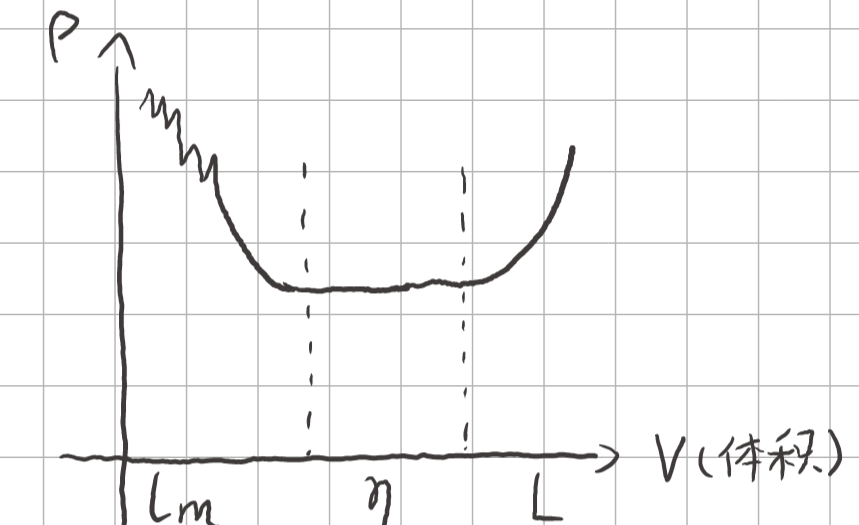
​本课程研究连续体尺度的问题。

一维稳态扩散及其求解

一维动量守恒

在高中阶段，我们已经学习了关于动量的两个基本公式：

\[P=mV\\\sum F=\frac{dp}{dt} \]

现在，让我们考虑一个流体微元，其体积为\(dV=Adx\)（参见下面讲控制体积时的图），质量为\(dm=\rho dV\)，速度为\(u\)。

（注意：这里\(u=\frac{dx}{dt}\)表示一个流体微元的位置x随着时间t的变化率；稳态下，\(\frac{\partial u}{\partial t}=0\)，即流体微元的运动速度在流场中的分布不随时间变化，但流体微元的位置x仍然会随着时间变化。）

其动量为：

\[dP=dm\cdot u=\rho dV u=\rho uA dx \]

其动量密度（每单位体积动量）为\(\rho u\)。

对于单位时间内，通过某一截面的动量：（注意\(dV=uA\)，其中A为截面面积）

\[动量流量=\rho (uA)u=\rho u^2 A \]

若只考虑一维，则可让A=1，动量流量=\(\rho u^2\)。

那么，对于该微元体积，其动量变化率为：

\[\frac{d(\rho u)}{dt}=\frac{\partial (\rho u)}{\partial t}+\frac{\partial(\rho u^2)}{\partial x} \]

注意Adx不随时间变化，上式表示动量密度随着时间和空间的变化。

假设流动是稳态的（不随时间变化），\(\frac{\partial(\rho u)}{\partial t}=0\)，则动量变化率可视为：

\[\frac{d(\rho u)}{dt}=u\cdot\frac{\partial(\rho u)}{\partial x}=\rho u\frac{\partial u}{\partial x} \]

根据动量定理，流体中动量的变化率等于外力作用：

\[-\frac{dp}{dx}=\rho u \frac{du}{dx} \]

其中，\(-\frac{dp}{dx}\)是压力梯度，\(\rho u\)代表质量流量，\(\frac{du}{dx}\)表示速度梯度。

令\(F(u)=\frac{1}{2} u^2\)：

\[\frac{dF(u)}{dx}=\frac{dF}{du}\cdot \frac{du}{dx}=u\frac{du}{dx} \]

\[-\frac{dp}{dx}=\rho u \frac{du}{dx}=\rho \frac{d(\frac{u^2}{2})}{dx} \]

这里，\(\frac{d(\frac{u^2}{2})}{dx}\)表示动能梯度。

所以，当流体从高压区流向低压区时，压力梯度驱使流体加速，压力变化转化为流体动能，导致速度和动量的变化。

进一步推导：

\[\int_{x_1}^{x_2} -dp=\int_{x_1}^{x_2} \rho d(\frac{1}{2}u^2) \]

\[\int_{p_1}^{p_2} -dp=\int_{u_1}^{u_2} \rho d(\frac{1}{2}u^2) \]

\[p_1-p_2=\frac{1}{2}\rho (u_2^2-u_1^2) \]

即伯努利方程。

一维稳态扩散

扩散通量：根据傅里叶定律，对于某个物理量\(\phi\)，单位面积上、单位时间内通过的量，与其梯度成正比。

\[J=-\Gamma \frac{d\phi}{dx} \]

‍

其中，\(\Gamma\)是扩散系数，因为扩散是从高浓度向低浓度，故这里用负号。

对扩散通量公式求导得：

\[\frac{dJ}{dx}=\frac{d}{dx}(-\Gamma \frac{d\phi}{dx}) \]

在稳态下，系统内部扩散的增减被源项平衡，即扩散通量变化与源项的和为0.

\[\frac{d}{dx} (\Gamma \frac{d \phi}{dx})+S(x,~\phi)=0 \]

扩散：任何物质（粒子、能量、动量...）由高浓度区域向低浓度区域传输，由浓度梯度驱动，无大规模物质对流。

式中：

• \(\phi\)表示待求的量（如温度、浓度、电势）；
• \(\Gamma\)表示扩散系数，\(\frac{d}{dx} (\Gamma \frac{d \phi}{dx})\)是扩散项，表示待求量扩散的速度和系数随着空间x变化，代表能量传递的过程；
• S表示源项（生成）或耗散项（消耗），与空间x、变量\(\phi\)相关，代表驱动能量传递的力量.
  在一维经壁热传导中，源项表示单位体积内热源或热汇的强度，如内部热源（材料本身由于其物理性质、化学反应，或内部有电阻，吸热、放热）。
  但高温区域、低温区域、墙壁构成的总系统的能量变化为0，系统内部能量守恒。

稳态：\(\frac{\partial}{\partial t}=0\)，时间不再影响\(\phi\)的变化，扩散过程已经达到平衡。

应用：

1. 剪应力的跨流扩散

   \[\frac{d}{dx}(\mu \frac{du}{dx})-\frac{dp}{dy}=0 \]

   ​​

   式中：

   • \(\mu\)是动态粘度，描述流体的剪切变形对剪应力的响应，反映了流体的粘性，是纯物质属性，单位\(N\cdot s/m^2\)；
   • v（这里未出现）是动力粘度，是动态粘度与流体密度的比值，反映了流体在重力作用下的扩散性；
   • \(\frac{du}{dx}\)表示速度梯度，反映了流体层之间的速度差异，\(\frac{d}{dx}(\mu \frac{du}{dx})\)代表剪应力的扩散；
   • \(\frac{dp}{dy}\)是压力梯度，表示驱动流动的压力差，作为动量的来源。当流动完全发展时，\(\frac{dp}{dy}=0\)；

   稳态：速度场和压力场不随时间变化；

   描述层流条件下的粘性流体，在粘性影响下，流体的各层相对滑动，产生剪应力。

一维稳态扩散的应用2：经壁热传导

1. 公式：

\[\frac{d}{dx}(\lambda \frac{dT}{dx})+S(x,~T)=0 \]

​
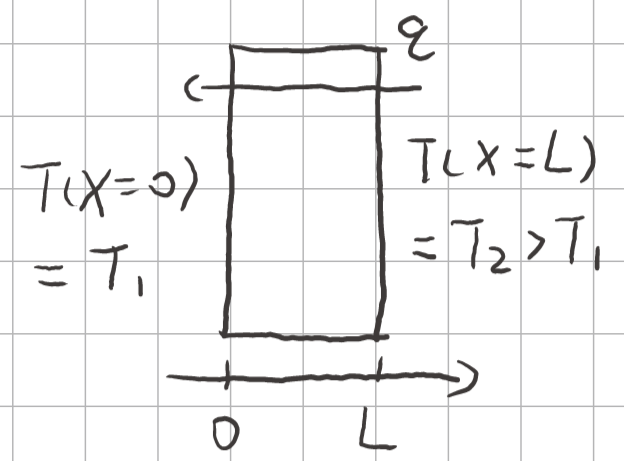
式中，\(\lambda\)为热导率，S代表系统中额外的热源/热汇。

边界条件：若绝热（adiabatic），\(\frac{\partial T}{\partial x}=0\)。

2. 如何求数值解

基本思路是离散化，目标是化为如下形式：

\[\left\{\begin{matrix}a_{1,~1}T_1+a_{1,~2}T_2+...+a_{1,~n}T_n \\... \\a_{n,~1}T_1+a_{n,~2}T_2+...+a_{n,~n}T_n \end{matrix}\right.\Longrightarrow [A][T]=[B] \]

在该矩阵中，\(a_{i,~j}\)表示描述第i个节点的控制方程中，和第j个节点（如左侧\(a_{i,~i-1}\)、自身\(a_{i,~i}\)、右侧\(a_{i,~i+1}\)）相关的系数；[B]表示所有不与温度相关的常数项。

​​

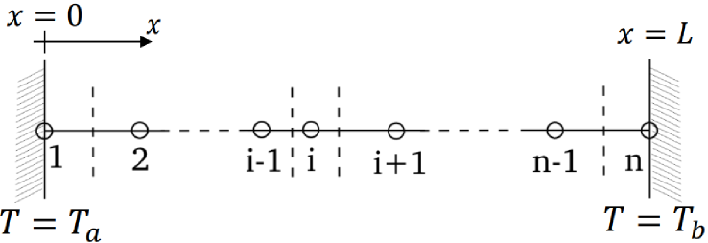
如图所示，在x=0到x=L的空间内取n个点测温。注意，点1在左边墙上，点n在右边墙上（即边界条件）。

这里有：

\[\Delta x=\frac{L-0}{n-1} \]

\[\frac{dT}{dx}\mid_i~\approx \frac{T_{i+1}-T_i}{\Delta x} \approx \frac{T_{i+1}-T_{i-1}}{2\Delta x} \]

离散化的具体实现：使用有限体积法，将整个域离散为n个控制体积（control volume，CV）。

注意：正在经历热传导的墙壁块是三维的；只是热传导的方向只有一条方向/一个维度。

​​

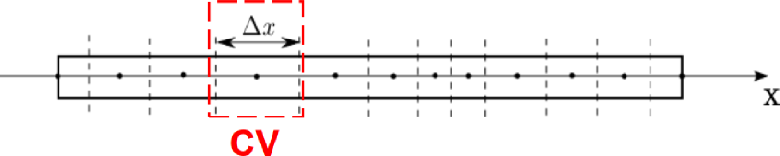
原公式如下：

\[\frac{d}{dx}(\lambda \frac{dT}{dx})+S(x,~T)=0 \]

根据控制体积，对上式进行积分，则有：

\[\int_v \frac{d}{dx}(\lambda \frac{dT}{dx})dV+\int_v S(x,~T)dV=0 \]

​​

​​

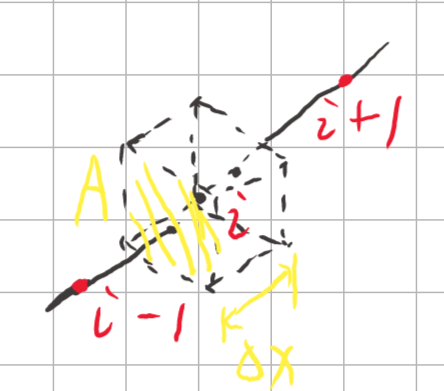
参见上图，有\(dV=Adx\)，则：

\[\int_w^e \frac{d}{dx}(\lambda \frac{dT}{dx})Adx+\int_w^e S(x,~T)Adx=0 \]

这里W意为west，E意为east。

​​

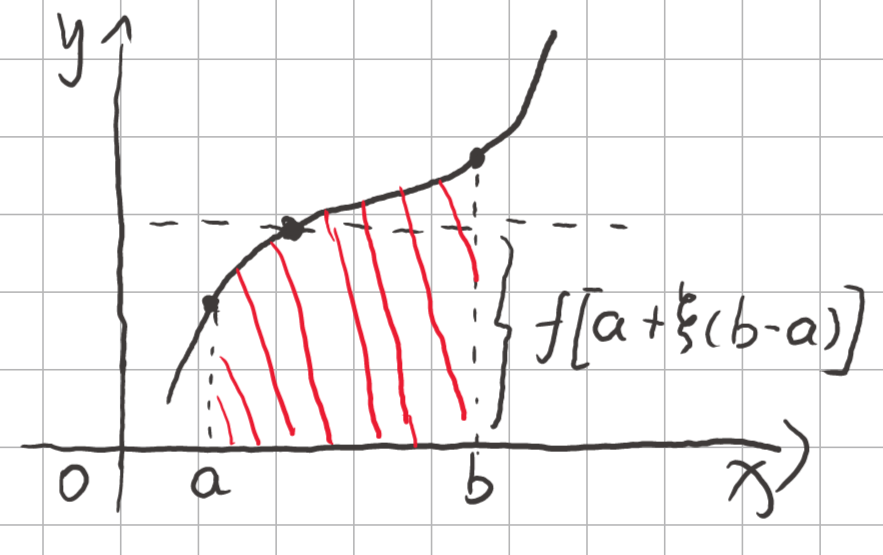
如图，设对阴影部分积分。

\[\int_a^b f(x)dx=f[a+\xi(b-a)]\cdot(b-a) \]

其中\(\xi\)是0~1之间的任意常数。

又有\(\int \frac{df(x)}{dx}dx=f(x)\)，则方程可化为：

\[[\lambda\frac{dT}{dx}]_{w}^{e}+\bar{S}[x]_w^e=0 \]

\[(\lambda \frac{dT}{dx})_e-(\lambda \frac{dT}{dx})_w+\bar{S} \Delta x=0 \]

其中\(\bar{S}\)是控制体积内S的均值，相当于把复杂的\(S(x,~T)\)简化，便于后续线性化。

1 数值方法A 续

‍