2 湍流

2 湍流

背景

湍流是具有广泛涡旋尺寸谱和相应波动频率谱的涡旋运动。

湍流具有如下特征：旋转、间歇性（intermittent）、高度无序性、扩散性（diffusive）、耗散性（dissipative）。

湍流可用纳维-斯托克斯动量方程描述。

最大的涡旋（低频波动）的形式通常由边界决定，最小涡旋（最高频波动）的形式由粘性力决定。

湍流的起源

有如下几种典型的空气流动状态：

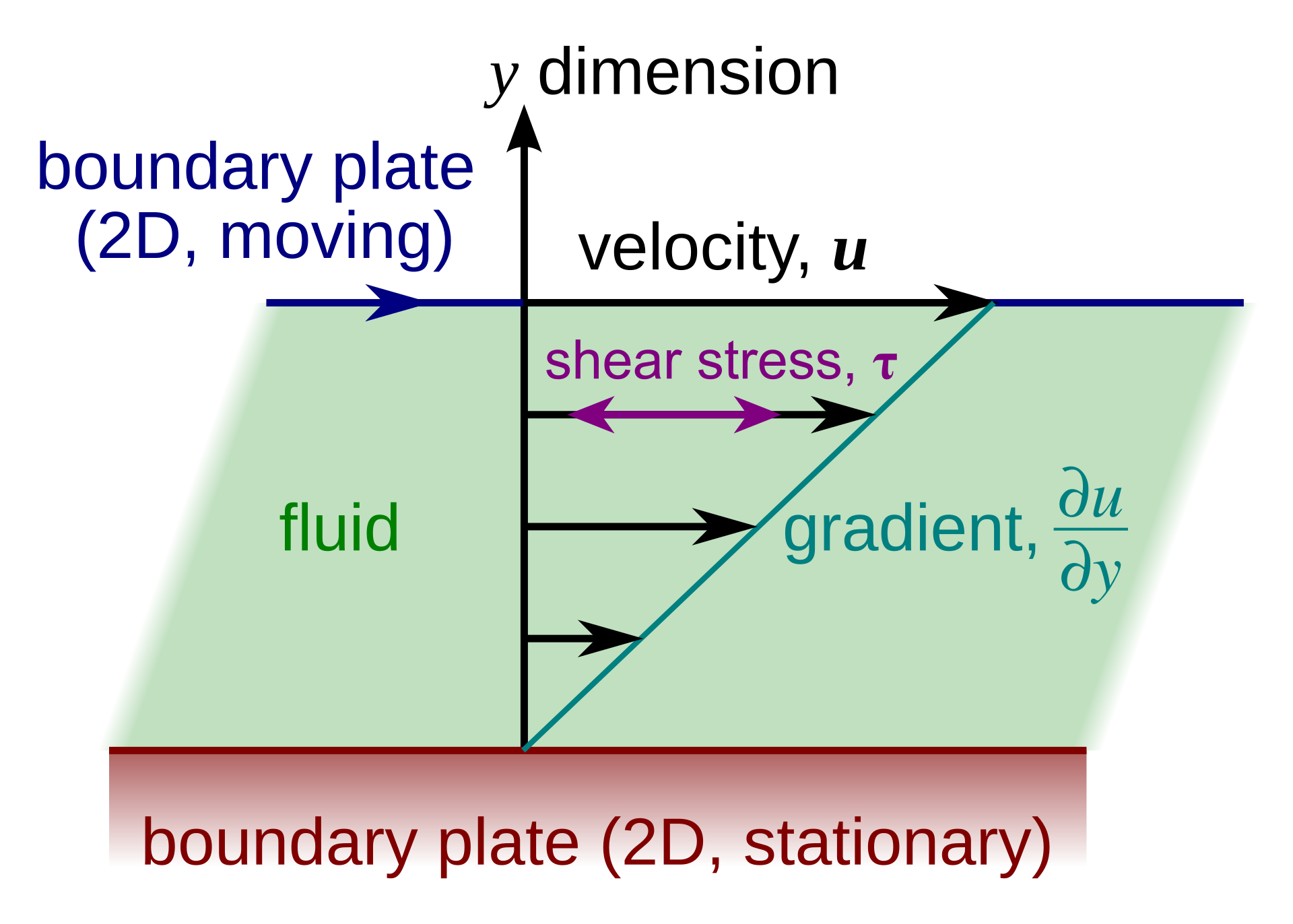
1. 库埃特流（couette flow）：两块平行板，其中一块板以恒定速度，相对另一块板移动，导致流体在黏性作用下被拖曳，形成剪切流动。
   层流状态下，速度沿垂直于板的方向线性分布。
   ​​
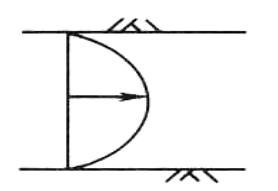
2. 通道流（channel flow）：两块固定的平行板之间，由压力梯度驱动的流动。
   稳态层流条件下，速度沿垂直于板的方向，呈抛物线形分布。
   ​​
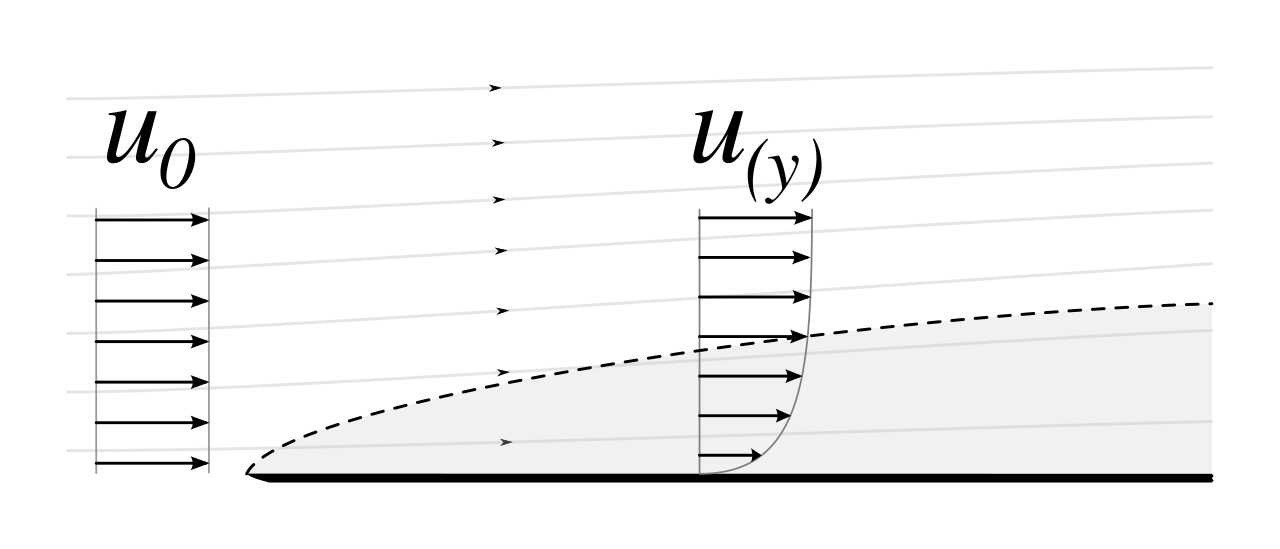
3. 边界层流动：流体在固体壁面附近，由于黏性作用，速度从0（壁面处的无滑移条件）逐渐增大到自由流速度。
   垂直于壁面的速度梯度很大。
   ​​

有以下3种典型的湍流状态：

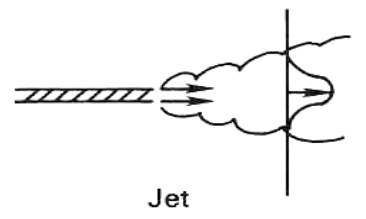
1. 射流（jet）：高速流体通过喷口或开口，进入静止或慢速环境时，由于喷口附近存在较大的速度差/速度梯度，该梯度引发了不确定性，在周围环境中产生剪切应力，导致湍流发展。
   如吹风机吹出的高速气流进入周围空气中。
   ​​
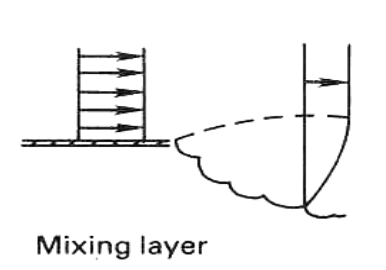
2. 混合层（mixing layer）：两股速度不同的平行流体之间的过渡区域中，由于速度差异，产生速度梯度，导致不确定性，产生滚动的涡结构，最终演化为湍流。
   大尺度的涡卷促进两股流体的混合。
   如打开教室门，外面的气压略高于里面的，有气流从教室外涌入，形成混合层。
   ​​
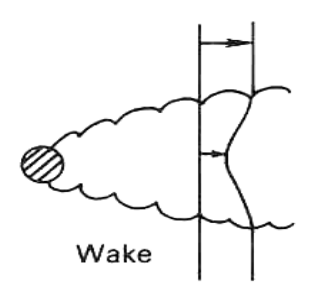
3. 尾流（wake）：当流体绕过物体时，由于边界层分离和压力梯度，物体后方形成低压区和涡流结构，产生尾流湍流。
   卡门涡街出现，涡旋交替脱落；尾流中的不稳定涡流导致压力脉动；尾流区域平均速度低于自由流速度。
   如桥梁的桥墩在水流中产生尾流湍流，形成涡街。
   ​​

时间平均雷诺方程

给定一物理量\(\varphi(t)\)，该物理量可代表流体的速度、压力等，其在时间上的均值（或稳态分量）为\(\Phi(t)\)，随时间波动的扰动分量为\(\varphi ^{'}\)。

\[\Phi=\frac{1}{T}\int_0^T\varphi(t)dt \]

\[\overline{\varphi^{\prime}}=\frac{1}{T}\int_{0}^{T}\varphi^{\prime}(t)dt\equiv0 \]

将\(\varphi(t)\)分解为时间平均+扰动分量：

\[\varphi = \Phi + \varphi ^{'} \]

给定另一物理量\(\psi (t)\)，其稳态分量为\(\Psi (t)\)，随时间波动的扰动分量为\(\psi ^{'}\)。

分解方法同上，有\(\psi = \Psi + \psi ^{'}\)。

在时间平均过程中，定义如下规则：

1. \(\overline{\varphi^\prime}=\overline{\psi^\prime}=0\)
   波动量是关于平均值的偏差，长时间而言，这些偏差的正负相互抵消，结果为0.

2. \(\bar{\Phi}=\Phi\)
   稳态分量的时间平均值始终等于其本身。

3. \(\frac{\partial\overline{\varphi}}{\partial s}=\frac{\overline{\partial\varphi}}{\partial s}\)
   左边意为先对物理量\(\varphi\)进行时间平均，再对其结果进行空间导数（这里的s不是拉普拉斯变换，而代表空间）；
   右边意为先对\(\varphi\)进行空间导数运算，再对导数结果进行时间平均。
   该规则意味着空间导数与时间平均操作是可以互换的。

4. \(\overline{\int\varphi ds}=\int\Phi ds\)
   类似条目3，空间积分操作和时间平均操作的先后顺序可以互换。

5. \(\overline{\varphi+\psi}=\overline\varphi+\overline\psi\)
   时间平均值的和等于各分量平均值的和。

6. \(\overline{\varphi^{\prime}\psi}=0\)
   波动量和稳态量乘积的平均值为0，表明波动量对稳态量没有显著影响。

7. 雷诺分解：

   \[\begin{aligned} \overline{\varphi(t)\psi(t)} &= \frac{1}{T} \int_0^T \varphi(t)\psi(t)dt\\ &= \frac{1}{T} (\Phi+\varphi^{'})(\Psi+\psi^{'})dt\\ &= \frac{1}{T} (\Phi\cdot \psi+\Phi \cdot \psi^{'}+\varphi^{'}\Psi+\varphi^{'}\psi^{'})dt\\ &= \frac{1}{T} (\Phi\cdot \psi+\varphi^{'}\psi^{'})dt\\ &= \Phi \Psi + \overline{\varphi^{'}(t)\psi^{'}(t)} \end{aligned} \]

   看到最后的式子，其中\(\Phi \Psi\)反映了两个变量的稳态之间的相互作用，\(\overline{\varphi^{'}(t)\psi^{'}(t)}\)量化的湍流引起的额外相互作用。

   注意，从步骤1到步骤2的拆括号，是将物理量分解为平均值和波动分量；
   从步骤3到步骤4的消元，是因为我们认为波动分量的时间平均值为0。

8. 梯度和散度：

   • 梯度描述一个标量场在空间中变化的最快方向和速率。
     对于一个标量场\(\varphi(x,y,z)\)：

     \[\nabla\varphi=\left(\frac{\partial\varphi}{\partial x},\frac{\partial\varphi}{\partial y},\frac{\partial\varphi}{\partial z}\right) \]

   • 散度表示向量场在各个方向上的变化和，描述一个向量场的“发散”程度，或者说这个场是否有源头或汇集。
     对于一个向量场\(\mathrm{u(x,~y,~z)~=~(u_x,~u_y,~u_z)}\)：

     \[\nabla\cdot\mathbf{u}=\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z} \]

   • 散度的时间平均：

     \[\overline{\nabla\cdot u}=\nabla\cdot\boldsymbol{U} \]

     时间平均操作下，向量场u的散度等于其平均场U的散度，即平均流动下，向量场的发散性没有因为波动部分而改变。

   • 质量守恒定律的时间平均应用：

     \[\overline{\nabla\cdot(\varphi\boldsymbol{u})}=\nabla\cdot\overline{(\varphi\boldsymbol{u})}=\nabla\cdot(\Phi\boldsymbol{U})+\nabla\cdot\overline{\varphi^{\prime}}\overline{\boldsymbol{u}^{\prime}} \]

     物理量标量场和速度场的乘积的散度，可以分解为平均值部分和波动部分。即使考虑到平均流动，也不能忽略波动部分对流动的影响。

   • 梯度的时间平均操作：

     \[\overline{\nabla\cdot\nabla\varphi}=\nabla\cdot\nabla\Phi \]

     一个标量场的时间平均值的梯度，等于该标量场平均值的梯度。即标量场的梯度只与其平均值有关，波动部分在平均后对整体物理量变化没有影响。

雷诺平均处理速度场

根据雷诺分解，一个瞬时速度可以被分解为平均速度和波动速度的和。

\[u(t)=\overline{U}+u' \]

计算时间平均速度：

\[\bar{u}=\frac{1}{T}\int_{t_0}^{t_0+T}udt \]

波动部分的时间平均值为零：

\[\frac1T\int_{t_0}^{t_0+T}\boldsymbol{u}^{\prime}dt=\overline{\boldsymbol{u}^{\prime}}=0 \]

若考虑所有三个速度分量，则有：

\[\overline{u^{\prime}}=\overline{v^{\prime}}=\overline{w^{\prime}}=0 \]

连续性方程

在不可压缩流动中，速度场的散度为0，流体体积保持不变，流入和流出的速度平衡。连续性方程描述了这一现象。

\[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 \]

通过雷诺平均，将速度分量分解为平均速度和波动速度，代入连续性方程中，并对每一项进行时间平均：

\[\frac1T\int_{t_0}^{t_0+T}\left(\frac{\partial(\overline{U}+u')}{\partial x}+\frac{\partial(\overline{V}+v')}{\partial y}+\frac{\partial(\overline{W}+w')}{\partial z}\right)dt=0 \]

从这一步可得：

\[\frac{\overline{\partial\bar{U}}}{\partial x}+\frac{\overline{\partial u^{\prime}}}{\partial x}+\frac{\overline{\partial\bar{V}}}{\partial y}+\frac{\overline{\partial v^{\prime}}}{\partial y}+\frac{\overline{\partial\bar{W}}}{\partial z}+\frac{\overline{\partial w^{\prime}}}{\partial z}=0 \]

注意，波动项对最终结果没有贡献，故：

\[\frac{\partial\overline{U}}{\partial x}+\frac{\partial\overline{V}}{\partial y}+\frac{\partial\overline{W}}{\partial z}=0 \]

这表明，即使在湍流中，平均速度场仍然必须满足不可压缩流体的连续性方程。

湍流中的动量输运

考虑一个体积为\(\delta x \delta y \delta z\)的小流体单元，设动量在x方向上的输运量为\(M_{xx}\)。

​​

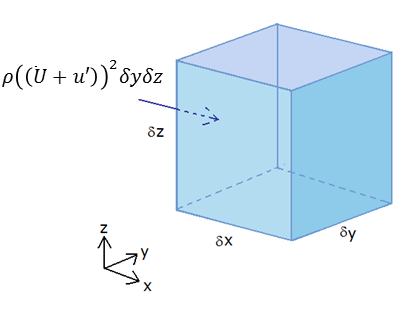
注意：动量的输运量=质量流量*流速

• 关于质量流量：

  1. 速度u表示流体在x方向上，单位时间内，流体移动的距离。
     流体在单位时间内，通过截面积\(\delta y \delta z\)的体积是\(u\delta y \delta z\)，这就是体积流量。
  2. 密度\(\rho\)表示单位体积内的质量，反映了流体的浓度。
     体积流量乘以密度，就得到了质量流量。

\[M_{xx}=(\rho u \delta y \delta z)u=\rho u^2 \delta y \delta z \]

平均动量输运\(\bar{M_{xx}}\)是通过单位表面积的平均动量通量，可表示为：

\[\bar{M}_{xx}=\rho(\bar{U}^2+\overline{(u^{\prime})^2}) \]

这里相当于把上面的\(\delta y \delta z\)消掉，然后把u拆成平均量和波动量；同时使用了波动量和平均量乘积为0的规则，得到该方程。

湍流是混乱、随机、多尺度的运动，流体粒子会在各个方向上产生不规则的运动。因此，在流体的湍流中，动量不仅沿着主流动方向输运，还会因为其他方向的流体运动（脉动速度），产生动量的传递。

让我们讨论y方向上的速度v引起的质量流量，对x方向动量的贡献，记为\(M_{xy}\)（在垂直于y轴的表面上的x方向动量，如经过上图的xz表面中心，有一个进入流体小块的速度，对图中已有的速度产生影响）：

\[\begin{aligned} M_{xy}& =(\rho v\delta x\delta z)u \\ &=\rho\delta x\delta zvu \\ &= \rho\delta x\delta z(\bar{V}+v')(\overline{U}+u') \\ &=\rho\delta x\delta z(\bar{V} \bar{U}+\bar{V}u'+\bar{U}v'+v'u')\\ &= \rho\delta x\delta z(\bar{V} \bar{U}+v'u') \end{aligned} \]

N-S方程的时间平均

雷诺代数

1. 笛卡尔张量指数表示：用符号\(x_i\)表示空间坐标，其中\(i=1,~2,~3\)分别对应x, y, z方向

2. 爱因斯坦求和约定：当一个表达式出现重复的索引时，隐含着对该索引从1到3的求和。如：关于连续性方程的表达式

   \[\frac{\partial U_i}{\partial x_i}=0 \]

   根据求和约定，该表达式等于：

   \[\frac{\partial U_1}{\partial x_1}+\frac{\partial U_2}{\partial x_2}+\frac{\partial U_3}{\partial x_3}=0 \]

   这样有利于将多个方向上的求和操作，简化为单个紧凑的表达式。

3. 对流（convection）项的表示：

   \[U_j \frac{\partial U_i}{\partial x_j}=\sum_{j=1}^3U_j \frac{\partial U_i}{\partial x_j}=U_1 \frac{\partial U_i}{\partial x_1}+U_2 \frac{\partial U_i}{\partial x_2}+U_3 \frac{\partial U_i}{\partial x_3}=0 \]

   对流项描述了流体质点由于自身运动，和速度场的空间变化共同作用，叠加引起的速度变化。
   假设有一条河，我们在河里划船，河水的流速在不同位置有所变化。
   \(U_j\)表示自身划船的速度；\(\frac{\partial U_i}{\partial x_j}\)表示河流在不同位置的水流速度不同，即河水流速在空间中的变化。

应用雷诺代数：N-S方程

1. 应力张量 ：描述流体内部因应变产生的力，包括压力和粘性剪应力的贡献。

   \[\sigma_{ij}=-p\delta_{ij}+2\mu s_{ij} \]

   其中：

   • p表示瞬时压力

   • \(\delta_{ij}\)是克罗内克符号，用于表示单位矩阵的元素，即当\(i=j\)时，\(\delta_{ij}=1\)，否则该符号表示的数为0

   • \(-p\delta_{ij}\)代表流体内部，由于静压力p引起的正应力（法向应力），它的作用垂直于流体微元的表面，导致流体受到压缩或膨胀。该压力各向同性。负号表示流体微元受到周围流体的挤压。

   • \(\mu\)是动力粘度，描述了流体的粘性性质

   • \(s_{ij}\)是应变速率张量，描述了流体速度场的对称梯度，定义为：

     \[S_{ij}=\frac{\partial U_i}{\partial x_j} \]
     \[s_{ij}=\frac{1}{2}\left(\frac{\partial v_i}{\partial x_j}+\frac{\partial v_j}{\partial x_i}\right) \]

   • \(2\mu s_{ij}\)反映了流体层之间，由于相对运动产生的内部摩擦力，它与速度梯度成正比，即流体流动越剧烈，产生的内部摩擦力越大。

2. 分解应力张量：

   \[s_{ij}=S_{ij}+s_{ij}' \]

   其中\(S_{ij}\)表示平均应变速率，即对应于时间平均流场的变形速率；
   ​\(s_{ij}^{'}\)表示脉动应变速率，描述湍流中瞬时流场相对于平均流场的变化。
   总应力张量\(\sigma_{ij}\)也被分解为：

   \[\sigma_{ij}=\Sigma_{ij}+\sigma_{ij}^{\prime} \]

3. 雷诺平均N-S方程 ：

原N-S方程为：

\[\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac1\rho\frac{\partial p}{\partial x_i}+\nu\frac{\partial^2u_i}{\partial x_j\partial x_j}+g_i \]

其中：

• \(\frac{\partial u_i}{\partial t}\)是局部加速度，表示流体速度在固定空间位置上，随时间的变化率；

• \(u_j\frac{\partial u_i}{\partial x_j}\)是对流加速度，表示由于流体在空间中移动，速度随着位置的变化导致的加速度。

• \(-\frac1\rho\frac{\partial p}{\partial x_i}\)是压力梯度力，表示流体受到的力推动其由高压区域流向低压区域，是流体运动的主要驱动力之一；

• \(\nu\frac{\partial^2u_i}{\partial x_j\partial x_j}\)（这里\(\nu=\frac{\mu}{\rho}\)念nu，是动力粘度系数）是粘性扩散项，表示流体内部由于粘性产生摩擦力，抵抗流体的变形和流动，起到能量耗散作用；

• \(g_i\)表示作用在流体上的外部力，如重力、磁力等。

• 整个方程左侧是加速度，右侧是合力/质量，体现了牛顿第二定律（\(\bar{F}=ma\)）。

  \[\frac{\vec{F}}{m}=\frac{d\vec{U}}{dt}=\frac{d\vec{U}}{ds}\frac{ds}{dt}=\vec{U}\cdot \frac{d\vec{U}}{ds} \]
  \[\frac{\vec{F}}{m}\cdot ds=\vec{U}d\vec{U}=d(\frac{\vec{U}^2}{2}) \]

推导RANS下的N-S方程：

1. 将瞬时变量分解为时间平均值和波动值的和：

   \[u_i=U_i+u_i';~p=P+p' \]

   u代表速度，p代表静压。

2. 将上述分解代入原方程，得：

   \[\frac{\partial(U_i+u_i')}{\partial t}+(U_j+u_j')\frac{\partial(U_i+u_i')}{\partial x_j}=-\frac1\rho\frac{\partial(P+p')}{\partial x_i}+\nu\frac{\partial^2(U_i+u_i')}{\partial x_j\partial x_j}+g_i \]

3. 分别计算各项的时间平均：

   利用以下性质：空间导数与时间平均操作是可以互换的；波动量的时间平均为0；波动量乘积的时间平均不一定为0.

   • 左边第一项（非稳项，局部加速度）：

     \[\frac{\partial(U_i+u_i')}{\partial t}=\frac{\partial U_i}{\partial t} \]

   • 左边第二项（对流项）：先展开。

     \[\overline{(U_j+u_j')\frac{\partial(U_i+u_i')}{\partial x_j}}=U_j\frac{\partial U_i}{\partial x_j}+\overline{u_j'\frac{\partial U_i}{\partial x_j}}+U_j\overline{\frac{\partial u_i'}{\partial x_j}}+\overline{u_j'\frac{\partial u_i'}{\partial x_j}} \]

     考虑波动量的时间平均为0，对流项展开后变成：

     \[U_j\frac{\partial U_i}{\partial x_j}+\overline{u_j^\prime\frac{\partial u_i^\prime}{\partial x_j}} \]

     关于其中的项\(\overline{u_j'\frac{\partial u_i'}{\partial x_j}}\)，我们进行如下推导：

     1. 根据莱布尼茨法则，有：

        \[\frac d{dx}(f(x)g(x))=f(x)\frac{dg}{dx}+g(x)\frac{df}{dx} \]

        反向利用一次，我们可以得到：

        \[u_j'\frac{\partial u_i'}{\partial x_j}=\frac{\partial}{\partial x_j}(u_i'u_j')-u_i'\frac{\partial u_j'}{\partial x_j} \]

     2. 考虑不可压缩流动：
        利用雷诺分解，已经有：

        \[\frac{\partial u_i}{\partial x_i}=\frac{\partial(U_i+u_i^\prime)}{\partial x_i}=\frac{\partial U_i}{\partial x_i}+\frac{\partial u_i^\prime}{\partial x_i}=0 \]

        在稳态、不可压缩流动中，平均速度场是无散的：

        \[\frac{\partial U_i}{\partial x_i}=0 \]

        故：

        \[\frac{\partial u_i^\prime}{\partial x_i}=0 \]
        \[u_j'\frac{\partial u_i'}{\partial x_j}=\frac{\partial}{\partial x_j}(u_i'u_j') \]

     3. 在时间平均（或称为统计稳态）条件下，平均值运算和空间导数可以交换。最终可得：

        \[\overline{u_j'\frac{\partial u_i'}{\partial x_j}}=\frac{\partial}{\partial x_j}\overline{u_i'u_j'} \]

     4. 最终的对流项为：

        \[U_j\frac{\partial U_i}{\partial x_j}+\frac{\partial}{\partial x_j}\overline{u_i'u_j'} \]

   • 右边第一项（压力梯度项）：

     \[-\frac{1}{\rho}\frac{\overline{\partial(P+p^{\prime})}}{\partial x_{i}}=-\frac{1}{\rho}\frac{\partial P}{\partial x_{i}} \]

   • 右边第二项（粘性扩散项）：

     \[\nu\frac{\overline{\partial^2(U_i+u_i')}}{\partial x_j\partial x_j}=\nu\frac{\partial^2U_i}{\partial x_j\partial x_j}+\nu\overline{\frac{\partial^2u_i'}{\partial x_j\partial x_j}} \]

     注意：通常，波动项的粘性扩散相对于湍流对流可以忽略，或在湍流模型中处理。也就是说，该等式右边第二项在这里先忽略不计。

4. 将上述时间平均后的项组合起来：

   \[\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}=-\frac1\rho\frac{\partial P}{\partial x_i}+\nu\frac{\partial^2U_i}{\partial x_j\partial x_j}-\frac\partial{\partial x_j}\overline{u_i^{\prime}u_j^{\prime}}+g_i \]

5. 引入雷诺应力张量：我们将等式右边的压力梯度项和粘性项统一，综合写成应力张量的散度形式。
   定义粘性应力张量为：

   \[\tau_{ij}=2\mu S_{ij} \]

   其中，应变率张量\(S_{ij}\)定义为：\(S_{ij}=\frac12\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\)
   我们将粘性应力对第i个方向的作用，表示为粘性应力张量的散度，并假设\(\mu\)为常数：

   \[\begin{aligned} \frac{\partial\tau_{ij}}{\partial x_j}&=\frac{\partial}{\partial x_j}(2\mu S_{ij})\\ &=\mu\left(\frac{\partial^2U_i}{\partial x_j\partial x_j}+\frac\partial{\partial x_j}\frac{\partial U_j}{\partial x_i}\right) \end{aligned} \]

   由于\(\frac{\partial U_j}{\partial x_j}=0\)（连续性方程），粘性应力张量的散度简化为：

   \[\frac{\partial\tau_{ij}}{\partial x_j}=\mu\frac{\partial^2U_i}{\partial x_j\partial x_j} \]

6. 定义关于压力和粘性应力的总应力张量为：

   \[\sigma_{ij}=-P\delta_{ij}+\tau_{ij}=-P\delta_{ij}+2\mu S_{ij} \]
   \[\frac1\rho\frac{\partial\sigma_{ij}}{\partial x_j}=\frac1\rho\frac\partial{\partial x_j}(-P\delta_{ij}+2\mu S_{ij}) \]

7. 最终得到的时间平均N-S方程为：

   \[\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}=\frac1\rho\frac\partial{\partial x_j}\left(-P\delta_{ij}+2\mu S_{ij}-\overline{\rho u_i^{\prime}u_j^{\prime}}\right)+g_i \]

   注意，如果想让等式两边的量纲到动量级别，需要同时乘以\(\rho\)。

雷诺应力

雷诺应力描述湍流的脉动对平均应力张量的贡献。
脉动即波动。

\[\tau_{ij}=-\rho\overline{u_i'u_j'} \]

其中，\(\overline{u_i'u_j'}\)是脉动速度分量的时间平均的乘积，代表两个方向上速度脉动的协方差。

协方差用于度量两个随机变量之间的线性相关性，这里定义为：

\[\mathrm{Cov}(u_i',u_j')=\overline{u_i'u_j'} \]

当协方差为正时，表示当\(u_i'\)偏离平均值为正时，\(u_j'\)也倾向于偏正；

当协方差为负时，表示两个脉动分量倾向于朝相反方向，偏离平均值；

当协方差为0时，表示两个脉动分量之间没有线性关联。

将其展开为矩阵形式：

\[\tau_{ij}=-\rho\begin{bmatrix}\overline{u_1'u_1'}&\overline{u_1'u_2'}&\overline{u_1'u_3'}\\\overline{u_2'u_1'}&\overline{u_2'u_2'}&\overline{u_2'u_3'}\\\overline{u_3'u_1'}&\overline{u_3'u_2'}&\overline{u_3'u_3'}\end{bmatrix} \]

其中，主对角线上的项表示沿各个方向的湍流动能（即脉动速度的方差），反映了湍流强度在相应方向上的大小；

非主对角线上的项表示不同方向上，脉动速度间的关联（或协方差），描述湍流中不同方向之间的相互耦合和动量交换。

对于笛卡尔坐标系（用u，v，w表示x，y，z方向上的流体速度），雷诺应力的矩阵形式可转化为：

\[\tau_{ij}=-\rho\begin{bmatrix}\overline{u^{\prime2}}&\overline{u^{\prime}v^{\prime}}&\overline{u^{\prime}w^{\prime}}\\\overline{v^{\prime}u^{\prime}}&\overline{v^{\prime2}}&\overline{v^{\prime}w^{\prime}}\\\overline{w^{\prime}u^{\prime}}&\overline{w^{\prime}v^{\prime}}&\overline{w^{\prime2}}\end{bmatrix} \]

几个重要问题：

1. 从物理角度，雷诺应力反映了湍流中通过脉动速度所引起的动量通量，其中：

   • 主对角线上的项描述了湍流如何在流动的主方向上增加流体的能量；
   • 非主对角线上的项描述湍流如何在不同方向上互相影响，这些项直接影响了湍流的旋转和剪切特性。

2. 为什么雷诺应力会有负号：
   它表示湍流的脉动对平均流动的减速作用，由于在湍流中，脉动脉动引起的动量传递，会对平均速度场施加额外的阻力。

3. 湍流封闭问题（closure problem）：
   引入雷诺应力项使得RANS方程组不能直接求解，因为\(\overline{u_i'u_j'}\)是新的未知量，此时方程的未知量多于方程数量。
   为了求解RANS方程，需要借助湍流模型近似这些应力。

((20241029145337-wduesg3 '2.1 湍流-续'))

湍流动能方程

闭合方法

现在，我们有10个未知数：1个平均压力P，3个平均速度分量\(U_i\)，6个雷诺应力分量\(\tau_{ij}\)；有4个方程：1个质量守恒方程，3个动量方程（每个方向一个）。

未知数多于方程数量，故无法直接求解湍流流场。

湍流动能的引入

平均流动动能方程

将时间平均N-S方程乘以\(U_i\)，并针对稳态流动进行简化，可得：

\[U_j\frac\partial{\partial x_j}\left(\frac12U_iU_i\right)= \frac{\partial}{\partial x_j}\left(-\frac{P}{\rho}U_i\right) +\frac{\partial}{\partial x_j}\left(2\nu U_iS_{ij}\right) -\frac{\partial}{\partial x_j}\left(\overline{u_i^{\prime}u_j^{\prime}}U_i\right)+P\delta_{ij}S_{ij} -2\nu S_{ij}S_{ij} +\overline{u_i^{\prime}u_j^{\prime}}S_{ij} \]

该能量平衡方程中各项的含义：

1. 左侧项\(U_j\frac\partial{\partial x_j}\left(\frac12U_iU_i\right)\)：平均流动动能的对流传递。
2. 右1 \(\frac{\partial}{\partial x_j}\left(-\frac{P}{\rho}U_i\right)\)：压力或流动做功
3. 右2 \(\frac{\partial}{\partial x_j}\left(2\nu U_iS_{ij}\right)\)：通过粘性应力的动能传递
4. 右3 \(-\frac{\partial}{\partial x_j}\left(\overline{u_i^{\prime}u_j^{\prime}}U_i\right)\)：通过雷诺应力的动能传递
5. 右4 \(P\delta_{ij}S_{ij}\)：压力对形变的做功
6. 右5 \(-2\nu S_{ij}S_{ij}\)：粘性耗散，将湍流能量转化为内能
7. 右6 \(\overline{u_i^{\prime}u_j^{\prime}}S_{ij}\)：湍流能量的生成

其中，雷诺应力项、粘性耗散项起着更大作用，而湍流能量生成项应为负值，表示平均动能不断被转化为湍流能量。

故简化后的方程如下：

\[U_j\frac\partial{\partial x_j}\left(\frac12U_iU_i\right)=\frac{\partial}{\partial x_j}\left(2\nu U_iS_{ij}\right)-\frac{\partial}{\partial x_j}\left(\overline{u_i^{\prime}u_j^{\prime}}U_i\right)-\overline{u_i^{\prime}u_j^{\prime}}S_{ij} \]

该方程表示雷诺分解后，平均流动的时间变化和空间输运。能量从平均流动，经湍流生产项传递到湍流。

湍流动能预算方程

将时间平均N-S方程乘以\(u_i\)，可得：

\[U_j\frac{\partial}{\partial x_j}\left(\frac{1}{2}\overline{u_i^{\prime}u_i^{\prime}}\right) = \frac{\partial}{\partial x_j}\left(-\frac{1}{2}\overline{Pu_j^{\prime}}\right) +\frac{\partial}{\partial x_j}\left(2\nu\overline{u_j^{\prime}s_{ij}^{\prime}}\right) -\frac{\partial}{\partial x_j}\left(u_j^{\prime}\frac{1}{2}u_i^{\prime}u_j^{\prime}\right) -2\nu\overline{s_{ij}^{\prime}s_{ij}^{\prime}} -\overline{u_i^{\prime}u_j^{\prime}}S_{ij} \]

这里同样，右2湍流动能传递项\(\frac{\partial}{\partial x_j}\left(2\nu\overline{u_j^{\prime}s_{ij}^{\prime}}\right)\)和右4粘性耗散项\(2\nu\overline{s_{ij}^{\prime}s_{ij}^{\prime}}\)比右1粘性传递项\(\frac{\partial}{\partial x_j}\left(-\frac{1}{2}\overline{Pu_j^{\prime}}\right)\)更重要。

注意到粘性耗散项，我们定义粘性耗散率\(\varepsilon\)为：

\[\varepsilon=2\nu{s_{ij}^{\prime}s_{ij}^{\prime}} \]

其中\(s_{ij}'\)是扰动流的应变率：

\[s_{ij}'=\frac{1}{2}\left(\frac{\partial u_i'}{\partial x_j}+\frac{\partial u_j'}{\partial x_i}\right) \]

该方程描述湍流动能（即雷诺分解后的波动项）的产生、输运和耗散过程。

当稳态流动中，对流与扩散局部平衡时（A=T），湍流的生成速率和耗散速率相等（P=\(\varepsilon\)）。

定义特征长度尺度\(\ell\)，描述湍流中能量含量最高的涡结构的空间尺度：

\[\ell=\int_0^\infty\overline{u_i'(x)u_i'(x+r)} dr \]

定义湍流的参考速度\(\vartheta\)，代表湍流中涡旋或脉动的典型速度大小：

\[\vartheta\approx\sqrt{\overline{u_i^\prime u_i^\prime}} \]

有如下关系式：

1. 湍流脉动应变率在能量耗散中占主导地位：

   \[\overline{s_{ij}'s_{ij}'}\gg S_{ij}S_{ij} \]

2. 在稳态湍流中，湍流动能的生产和耗散达到平衡：

   \[P=\varepsilon\Rightarrow-\overline{u_i'u_j'}S_{ij}=2\nu\overline{s_{ij}'s_{ij}'} \]

   其中，P是湍流动能的生产率，\(\varepsilon\)是湍流动能的耗散率；
   \(-\overline{u_i'u_j'}S_{ij}\)表示由于平均速度梯度引起的湍动能生产，\(2\nu\overline{s_{ij}'s_{ij}'}\)表示由于黏性作用导致的湍流动能耗散。

3. 平均应变率与参考速度和特征长度尺度的关系：

   \[S_{ij}\sim\frac\vartheta\ell \]

4. 湍流雷诺应力和参考速度的关系：

   \[-\overline{u_i^{\prime}u_j^{\prime}}\sim\vartheta^2 \]

5. 将关系3和4代入湍流动能的能量平衡方程2：

   \[\vartheta^2\cdot\frac\vartheta\ell \sim 2\nu\overline{s_{ij}^\prime s_{ij}^\prime} \]

   加入一个调整量纲的常数\(C_1\)：

   \[C_1\vartheta\ell S_{ij}S_{ij}=2\nu\overline{s_{ij}^{\prime}s_{ij}^{\prime}} \]

   整理得：

   \[\frac{\vartheta\ell}{\nu}S_{ij}S_{ij}=\overline{{s_{ij}^{\prime}s_{ij}^{\prime}}} \]

   这意味着湍流的脉动应变率可以通过参考速度、特征长度尺度、动力粘性系数和平均应变率描述。

几个重要定义

1. 涡粘性（eddy viscosity）：模拟湍流中涡流对动量传输的影响。

   \[\nu_t\propto\sqrt{k}\cdot L \]

   其中k是湍流动能，L是湍流的参考尺度。
   其单位为\(m^2/s\)，即速度\(\times\)长度尺度。

2. 湍流动能（turbulent kinetic energy）：表示湍流中速度波动的平均动能。

   \[k=\frac12\left(\overline{u'^2}+\overline{v'^2}+\overline{w'^2}\right) \]

3. 湍流的雷诺数：用于衡量涡流的强度。

   \[R=\frac{\nu_t}\nu=\frac{C_1\sqrt{k}L}\nu \]

描述湍流的理论

混合长度理论

​​

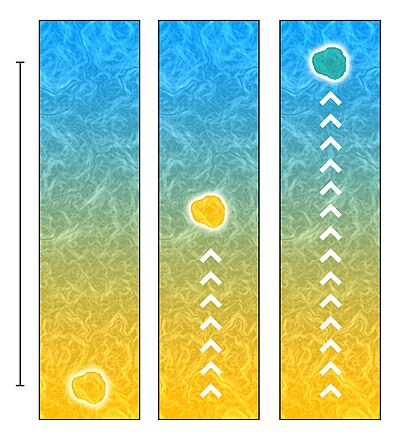
该理论提出，流体团在一个梯度上移动（如上图所示的温度梯度），混合长度（上图左侧的标尺）是这团流体与附近流体充分混合前（或理解为以整体移动时）所移动的距离。在移动过程中，流体团保持自身的物理性质，直到与周围介质混合。

在湍流中，速度波动分量使得流体微团不断相互混合：假设有一个速度较大的流体微团，从高速区域移动到低速区域，它将带去部分动量，使得低速区域的速度增加。这一过程导致了动量亏损或动量增益，也就产生了雷诺应力。

​​

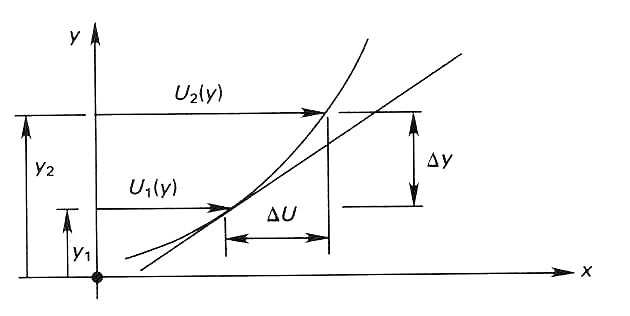
这张图描述了位置y1和y2处的不同速度\(U_1 (y)\)和\(U_2 (y)\)，此时两点之间的距离为\(\Delta y\)，速度差为\(\Delta U\)。

在位置y2处的动量亏损近似为：

\[\rho \Delta U\sim\rho\Delta y\frac{\partial U}{\partial y} \]

两边同时乘以 垂直方向 上的速度波动分量\(v'\)，可得湍流的平均动量通量（momentum flux，或每单位面积的动量传输）为：

\[(\rho\Delta U)v'\sim\rho\Delta yv'\frac{\partial U}{\partial y} \]

假设在某个横向距离l（即混合长度）处， 垂直速度波动 ​ \(v'\) ​ 和垂直间距 ​ \(\Delta y\) ​ 之间的相关性消失 。

此时，时间平均后的动量通量应为：

\[\rho\overline{v'}\cdot l\frac{\partial U}{\partial y} \]

平均动量通量等价于剪应力分量\(\tau_{xy}\)：

\[\tau_{xy}=c_1 \rho \bar{v'}\cdot l \frac{\partial U}{\partial y} \]

其中，\(c_1\)是用于调整涡流大小的常数。

下一步，参照牛顿粘性定律\(\tau=\mu \frac{dU}{dy}\)，定义一个湍流涡粘性系数（turbulent eddy viscosity coefficient）​\(\nu_t\)（再次注意，这里\(\nu\)​仍然念nu，不是速度那个v），用于扮演类似于分子粘性\(\nu\)的角色，描述湍流中的动量传递：

\[\nu_t=c_1\overline{v'}\cdot l \]

这样，剪应力分量可以表示为：

\[\tau_{xy}=\rho \nu_t \frac{\partial U}{\partial y} \]

接下来，对于简化的二维湍流流动，唯一显著的雷诺应力分量为：

\[\tau_{xy}=\tau_{yx}=-\rho\overline{u'v'} \]

唯一显著的速度梯度是\(\frac{\partial U}{\partial y}\)。

假设湍流中的垂直速度波动\(\bar{v'}\)可以用混合长度l和速度梯度估计，其中c是一个常数：

\[\overline{v'}=cl\left|\frac{\partial U}{\partial y}\right| \]

注意前面描述剪应力分量的方程，我们将所有常数合并成一个新的长度尺度\(l_m\)，可得涡粘性系数的新表达形式：

\[\nu_t=l_m^2\left|\frac{\partial U}{\partial y}\right| \]

这样我们可以得到剪应力的最终表达式：

\[\tau_{xy}=\tau_{yx}=-\rho\overline{u^{\prime}v^{\prime}}=\rho\ell_m^2\left|\frac{\partial U}{\partial y}\right|\frac{\partial U}{\partial y} \]

标准k-\(\varepsilon\)理论

方程

首先，根据Kolmogorov-Prandtl模型，我们定义湍流粘性系数\(\nu_t\)为：

\[\nu_t=C_\mu^{\prime}\sqrt{k}\cdot L \]

其中，\(C_\mu^{\prime}\)是经验常数，k是湍流动能，L和前文的\(\ell\)相同，代表湍流的特征长度尺度。

在该理论中，定义湍流能量耗散率（逐渐转化为内能）为：

\[\varepsilon\propto\frac{\vartheta^3}L \]

注意，这里\(\vartheta\)是湍流的参考速度。

我们令\(\vartheta \equiv \sqrt{k}\)，那么湍流能量耗散率变成：

\[\varepsilon=C_D\frac{k^{3/2}}L \]

其中\(C_D\)是与湍流模型有关的常数。

由如上公式，推导出湍流涡粘性常数的最终表达式：

\[\nu_t=C_\mu'C_D\frac{k^2}{\varepsilon}\Rightarrow\nu_t=C_\mu\frac{k^2}{\varepsilon} \]

考虑对湍流动能预算方程的简化：

• 扩散：湍流动能k和湍流能量耗散率\(\varepsilon\)中都出现了扩散项，它是由湍流的涡流效应主导的。
  在标准k-\(\varepsilon\)模型中，使用一个与梯度成比例的涡系数描述湍流扩散。

• 生产：湍流动能和能量耗散率中的生产项，描述了主流（平均流动）中的应变如何把能量传递给湍流。
  在标准k-\(\varepsilon\)模型中，假设湍流能量和耗散的生产，与平均流动的应变率张量\(S_{ij}\)成正比：

  \[S_{ij}=\frac{1}{2}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right) \]

得到湍流动能k的输运方程：

\[\frac{\partial k}{\partial t}+U_i\frac{\partial k}{\partial x_i}=\frac\partial{\partial x_i}\left(\frac{\nu_t}{\sigma_k}\frac{\partial k}{\partial x_i}\right)+\nu_t\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\frac{\partial U_i}{\partial x_j}-\varepsilon \]

湍流能量耗散率\(\varepsilon\)的输运方程：

\[\frac{\partial\varepsilon}{\partial t}+U_i\frac{\partial\varepsilon}{\partial x_i}=\frac\partial{\partial x_i}\left(\frac{\nu_t}{\sigma_\varepsilon}\frac{\partial\varepsilon}{\partial x_i}\right)+C_{1\varepsilon}\frac\varepsilon k\nu_t\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\frac{\partial U_i}{\partial x_j}-C_{2\varepsilon}\frac{\varepsilon^2}{k} \]

这里，定义湍流涡粘性常数\(\nu_t\)为：

\[\nu_t=C_\mu\frac{k^2}{\varepsilon} \]

注意上述3个方程中的常数分别为：

\[C_\mu{=}0.09,C_{l\varepsilon},{=}1.44,C_{2\varepsilon},{=}1.92,\sigma_k{=}1.00\mathrm{~and~}\sigma_\varepsilon{=}1.30 \]

边界条件

使用标准k-\(\varepsilon\)模型计算时候，不同区域需要不同边界条件定义湍流变量。

常见的边界条件有：

• 入口：需要给定湍流动能k和湍流动能耗散率\(\varepsilon\)。

  1. 湍动能

     \[k=\frac32(U_\infty T_i)^2 \]

     其中，\(U_\infty\)是自由流速度，\(T_i\)是湍流强度。

  2. 湍流动能耗散率

     \[\varepsilon=C_\mu^{3/4}\frac{k^{3/2}}\ell \]

     其中，\(C_\mu\)是常数，\(\ell\)是特征长度尺度，这里定义：

     \[\ell=0.07L \]

• 出口或对称轴：假设湍流动能和耗散率在法向方向上的导数为0

  \[\frac{\partial k}{\partial n}=0,~\frac{\partial\varepsilon}{\partial n}=0 \]

• 自由流：湍流动能和耗散率均为0，即k=0，\(\varepsilon=0\)​

• 固体壁面条件：壁面附近存在一个很薄的粘性子层，直接计算这一层的湍流非常复杂，故采取壁面函数法简化计算。

  1. 使用局部平衡假设：在一定范围内（\(30<y_p^+ <500\)），湍流的生产率P与耗散率\(\varepsilon\)相等

  2. 湍流边界层结构
     ​
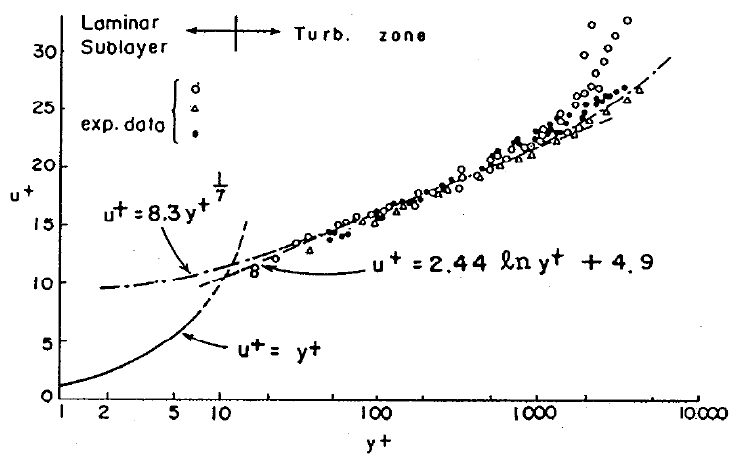
     在湍流边界层中，流动区域分为：

     • 层流子层（laminar sublayer）或粘性子层：速度剖面与到壁面的距离呈线性关系。

       \[u^+=y^+ \]

       通常应避免将第一个网格点设定在粘性子层内。

     • 缓冲层（buffer layer）：介于层流子层和对数层之间，流动之间变得不稳定。

     • 对数层（log layer）：速度剖面满足对数规律。

       \[u^+=2.44~lny^++4.9 \]

     • 湍流核心区（turbulent core zone）：远离壁面的区域，流动完全由湍流主导。

     • 值得注意的是，在高雷诺数条件下，粘性主导的子层非常薄，难以在数值计算中直接求解这一区域，故通常采用近似模型处理。

  3. 壁面法则：

     \[u^+=\frac{U}{u_\tau}=\frac{1}{\kappa}\ln(Ey_p^+) \]

     其中，\(u^+=\frac{U}{u_\tau}\)是无量纲的速度（这里\(u_\tau=\sqrt{\frac{\tau_w}{\rho}}\)是摩擦速度，\(\tau_w\)是壁面剪应力），\(\kappa=0.4\)是冯.卡门常数，E=9.8是壁面粗糙度参数，\(y_p^+\)是无量纲的法向距离。
     湍流动能和耗散率的壁面关系：

     \[k=\frac{u_\tau^2}{\sqrt{C_\mu}},\quad\varepsilon=\frac{u_\tau^3}{\kappa y} \]

     壁面边界条件通常包括：

     • 滑移条件（slip condition）：在壁面处施加剪应力，使得速度\(u\ne 0\)​
     • 湍流动能k：通常设定为零梯度
     • 耗散率\(\varepsilon\)：湍流生产和耗散达到平衡。

  4. ‍

  5. \(y^+\)
     ​\(y^+\)是一个无量纲参数，用于描述壁面附近的流动特性，表示壁面附近的第一个网格单元与壁面之间的距离。

     \[y^+=\frac{\rho u_\tau y_p}\mu \]

     注意，这里\(y_p\)才是真正的第一个网格单元到壁面的法向距离。
     \(y^+\)本质上是一个基于壁面附近单元尺寸的雷诺数，当该值很小（接近0）时，表示网格单元处于流动的粘性子层；\(30<y_p^+ <500\)范围内，流动符合对数定律层，湍流的主要特性由对数速度剖面描述。
     一般第一个网格单元必须放在符合对数层规律的区域内。
     估算\(y^+\)的方法：

     • 求摩擦系数\(c_f\)：

       \[c_f=\frac{\tau_w}{\frac12\rho U_e^2} \]

       其中，\(U_e\)是边界层以外的自由流速度。

     • 求摩擦速度\(u_\tau\)：

       \[c_f=\frac{u_\tau^2}{\frac12U_e^2}\quad\Rightarrow\quad u_\tau=U_e\sqrt{\frac{c_f}2} \]

       此外，可使用经典的摩擦系数关系：

       1. 平板流动

          \[\frac{c_f}2\approx0.052Re_x^{-0.142}=0.052\left(\frac{\rho U_ex}\mu\right)^{-0.142} \]

          其中，\(Re_x=\frac{\rho U_ex}\mu\)是基于位置x的雷诺数。

       2. 管道流动

          \[\frac{c_f}2\approx0.046Re_x^{-0.2}=0.046\left(\frac{\rho U_ex}\mu\right)^{-0.2} \]

          ‍

网格划分

几何形状

一般建议使用四边形或六面体单元（二维-四边形，三维-六面体），能更好捕捉流动的特征，减少数值耗散。

对于复杂几何形状，可使用混合网格：二维-四边形+三角形，三维-六面体、棱柱、四面体。

网格自适应

有时，为确保网格能捕捉所有流动特征，可对整个网格进行全局加密。

ANSYS Fluent软件提供网格自适应（mesh adaption）功能，可基于前一次解的参数值进行局部网格加密。

一般而言，建议相邻单元的网格密度比尽可能小，确保小于2:1，建议值约在1.3:1上下。

Kolmogorov能量级联

回顾一下，流体流动的动能包括时间平均速度和湍流脉动速度的贡献：

\[E=\frac12\rho\overline{u^2}=\frac12\rho\overline{(\bar{U}+u')^2}=\frac12\rho\left[\overline{(\bar{U})^2}+\overline{(u')^2}\right] \]

这样，湍流贡献的动能表示为：

\[\frac12\rho\overline{(u')^2} \]

这部分能量来自速度脉动，由不规则的小涡结构引起速度变化，这些涡结构是湍流中能量传递的主要机制。

在涡流中，大涡结构含有较高的能量，但由于它们不稳定，会逐渐分裂为更小的涡结构，此时大涡结构的能量逐级传递到更小的涡结构，而当能量传递到非常小的尺度时，这些能量会通过粘性耗散，转化为热能（或内能）。这就是能量级联（energy cascading） 。

​​

这张图是湍流的动能谱，将动能\(KE(k)\)作为波数k的函数绘制。波数k是涡结构的无量纲尺度，定义为：

\[k=\frac{\pi}{l} \]

这里l是涡结构的特征长度。

波数k表示涡结构的尺度，较大的涡结构具有较低的波数，能量较大；，较小的涡结构具有较高的波数，能量较低。

1. 区域I：能量含量区域（energy containing range）
   包含大尺度涡，携带了大部分的湍流能量，是流动中主要的能量来源，但相对不稳定。
   定义能量进入级联的速率\(E_I\)，它表示大涡产生能量，并开始向小涡传递能量的速率：

   \[E_I=\frac{d(\text{KE})}{dt}\sim\frac{d({u'}^2)}{dt}\sim\frac{{u'}_0^2}{L/{u'}}\sim\frac{{u'}_0^3}{L} \]

   其中，\({u'}_0\)是与大尺度涡相关的脉动速度，L是与大涡结构相对应的特征长度。
   定义大涡的周转时间，表示一个大涡完成一次循环（或旋转）所需的时间，它决定了能量传递的速度，因为如果一个大涡需要很长时间绕一圈，能量向小涡的传递速度就会变慢：

   \[\text{周转时间}=\frac{L}{{u'}_0} \]

2. 区域II：惯性子区域（inertial subrange），由于非线性相互作用（不是粘性力），大尺度涡结构逐渐崩解，能量按照固定速率，逐渐从较大的涡结构传递给较小的涡结构，而没有明显的能量耗散。
   该子区域中的能量传递速度，和区域I的能量传递速率\(E_I\)相等，表明能量从大涡到小涡的传递过程中没有能量损失。
   能量谱E(k)满足Kolmogorov能谱定律：

   \[E(k)=K_0\varepsilon^{2/3}k^{-5/3} \]

   其中，E(k)是波数k处的湍流动能；\(K_0\)是Kolmogorov常数，取值范围在1.4~1.7.

3. 区域III：耗散区域（dissipation range），小涡结构主导，粘性效应开始起作用，将湍流能量耗散为热能。这些最小尺度的涡结构也称为Kolmogorov尺度涡。
   能量耗散率公式为：

   \[\varepsilon\sim\frac{\nu u_k^{\prime2}}{L_k^2} \]

   其中，\(\nu\)是流体的动力粘性系数，\({u_k}'\)是与小涡相关的速度脉动，\(L_k\)是小涡相关的特征长度，即Kolmogorov长度尺度。
   涡结构越小，能量耗散速率越高。

值得注意的是，系统中所有进入湍流系统的能量，最终都需要通过耗散变成热能。也就是说，在大尺度涡区域生成的能量，必须在小尺度涡结构中被耗散掉。

‍