搜索推荐论文速读2
1. A Model-Agnostic Causal Learning Framework for Recommendation using Search Data. WWW 2022
从因果分析的角度看,用于表示特征的embedding向量与用户的点击反馈有着复杂的关系。作者认为,这种复杂的关系可以分为两部分,描述用户偏好某个item原因的causal part,以及反映用户与item统计依赖关系的non-causal part。前者是我们最希望模型学会如何建模的,后者是我们希望模型避免受到影响的(如position bias,selection bias, popularity bias等)。
本文的核心思想就是通过引入工具变量来剔除non-causal part的影响,从而让模型去除偏差获得更好的性能。
1.1 什么是工具变量?
工具变量,主要用于评估一个treatment变量 X 与结果变量 Y,在同时受到其他变量(confounders)的影响下,两者之间的因果关系(causal effect)。
原文表述:In causal inference, the
method of IVs [1, 5] aims to estimate the causal effect between a
treatment variable 𝑋 and an outcome variable 𝑌, in the presence
of other variables (e.g., confounders) that are associated with the
treatment and outcome simultaneously.
理论上来说,工具变量 Z 不受到confonder的影响(或者这种影响很小,几乎观测不到),并且只能通过Treatment X 影响到结果 Y 变量。现有利用工具变量的方法(如2SLS),一般都使用两阶段的最小二乘法来找出 treatment X 以及结果变量 Y 的因果关系:首先在工具变量上拟合treatment并获得重构treatment(学习 Z->X 的映射关系,因为不受confounder的影响,所以输出与X不完全相同,这个输出经过一些操作/不操作 成为重构的X),然后利用重构treatment拟合结果变量Y(学习 reconstruct treatment->Y 的映射关系),最后第二步拟合得到的映射关系,即treatment X与结果变量Y之间的无偏因果关系估计。
1.2 为什么使用工具变量?
如下图左侧的图(a)-传统推荐系统的因果图所示,\(T_{u,i}\) 是我们模型输入的用户-物品特征(embedding可视做为因果推断中的treatment),\(Y_{u,i}\)是最终预测的结果(如CTR模型预测的CTR,可是作为因果推断中的结果),我们希望模型能够学会两者之间的映射关系。但从因果推断的角度看,我们希望学习的映射关系里包含了causal part和non-causal part,non-causal part是造成模型性能偏差的主要原因。因果学习的框架中为了能够去除confounder的影响,常用的技巧是引入不受confounder影响的工具变量,利用工具变量就分离出我们真正想要因素的影响。(如下图右侧的图(b)所示,\(Z_{u,i}\) 即引入的工具变量)

在本文中工具变量具体的含义是“用户历史搜索中与候选推荐物品重合的搜索行为”,通过这个工具变量 \(Z_{u,i}\) 我们就可以将传统推荐系统的 \(T_{u,i}\) 拆解为不受confounder影响的causal part \(\hat{T}_{u,i}\)(通过对 \(Z_{u,i}\) -> \(\hat{T}_{u,i}\) 的拟合)以及其残差 \(\widetilde{T}_{u,j}\)。 \(\hat{T}_{u,i}\) -> \(Y_{u,i}\) 即为我们真正想要的causal part。
1.3 模型结构设计
在具体的结构设计中,文中先明确定义因果图中的每一个节点的含义:
treatment \(T_{u,i}\) 的具体含义是特征embedding的集合,包含候选物品、用户行为、上下文等的特征。
工具变量 \(Z_{u,i}\) 的具体含义是与候选物品相关的query embedding矩阵(使用BERT编码)。这里选择的query是在搜索系统中,搜索结果与候选物品相关的query,这些query还可经过排序(如按候选物品的点击率)来取top k个。

如上图所示,网络左侧的图的是粗略的总体框架图。由于本文所提的模型是 model-agnostic 的,总体框架图中的橙色框 Underlying model 可以替换成其他模型结构,本文所提模块(蓝色框)起作用的层次仅在原始特征输出层,用于消偏,消偏特征如何使用完全自由。在本文所提模块的输出\(t_{n}^{re}\)后,可以接任意的模块,比如你想学习用户行为序列信息的话就可以加attention。
本文的核心结构(上图的最右侧子图)总体上可以划分为:treatment decomposition、treatment combination两个基本部分。这里为了方便读者理解数据流向及变化,省略了原文汇总的一大堆公式描述(主要是懒得逐个敲公式),仅以文字描述的方式介绍。
treatment decompositon:这一部分对应使用工具变量的第一阶段,即使用最小二乘法拟合“工具变量\(Z_{u,i}\) => treatment \(T_{u,i}\)”的映射,得到 \(\hat{T}_{u,i}\) 。在图中体现就是工具变量 \(Z_{j}\) 经过 \(f_{proj}: R^{d_{i}} \times R^{d_{q}\times N} -> R^{d_{q}}\) 做维度变换后得到的 \(\hat{t}_{j}\),优化其与 用户特征 \(t_{j}\)(经过 \(MLP_{0}\) 的非线性变换)的MSE loss。
得到 \(\hat{t}_{j}\) 后,很自然的就可以计算出残差 \(\widetilde{t}_{j}\),其值是 \(MLP_{0}(t_{j}) - \hat{t}_{j}\)
treatment reconstruction:说白了就是将 \(MLP_{0}(t_{j})\) 与 \(Z_{j}\) concat 后分别经过两个 MLP 降维为1 获得 两个加权系数 \(\alpha_{j}^{1}\) 与 \(\alpha_{j}^{2}\) 与 \(\hat{t}_{j}\) , \(\widetilde{t}_{j}\) 加权求和就好了。
2. Unbiased Delayed Feedback Label Correction for Conversion Rate Prediction. KDD2023
在推荐/搜索系统中,用户点击后是否真实做出正向反馈(如下载app、购买商品等)对衡量推荐是否有效十分重要,这种正向反馈也是直接产生收益的。衡量这种正向反馈的指标是CVR(Conversion Rate)。
但是直接让模型学会从物品信息、用户信息中学会去预测这个数值存在延迟反馈的问题。所谓延迟反馈,即由于物品被点击到真正转化成收益的过程是相对漫长(如几天、几个星期之后)、不确定的(可能转化,可能不转化),训练模型所使用的一定时间间隔内的数据,不一定是所有物品都完成转化的数据,因此标签为“未转化”的数据样本可能在未来转化,也可能不转化。这个训练数据中问题,反映到模型学习上,会使得模型出现“延迟反馈偏差”。
本文旨在缓解这种偏差,提出了一种基于反事实的损失函数,并设计了相对应的网络结构(单独设计一个网络用来估计已知时间段内成功转化的概率)。
2.1 延迟反馈问题的数学建模
0-T时间间隔内收集到的数据集中,每一条数据包含如下五元组的信息:
其中:
- \(x_{i}\):样本的特征信息
- \(v_{i}\):独热值,表示物品在0-T时间间隔内,被推荐物品是否成功转化(Yes为1,No为0)
- \(e_{i}\):取值为 \(T-cts_{i}\),表示物品被点击后距离T的间隔时长
- \(cvt_{i}\):推荐物品成功转化的时间戳
- \(cts_{i}\):物品被点击的时间戳
- \(c_{i}\):物品最终是否转化成功,这是一个当前不可能获得的真实值
- \(w_{a}\):物品被点击后到完成转化的时间窗口
定义了上述符号后,反馈延迟问题就可以通过如下式子来表达:
被推荐物品最终是否成功转化一般标注为独热值,即模型可以建模为一个分类问题,可用交叉熵作为损失函数。若我们观测到的数据中所有的标签都是真实值 \(c_{i}\),则此时的交叉熵损失被称为 \(L_{oracle}\)。若标签是由延迟反馈的,则此时的交叉熵损失称为 \(L_{vanilla}\)
显然,我们最终希望得到的模型是由 \(L_{oracle}\)训练得到的。
2.2 本文方法介绍
作者认为,如果我们能够准确预测出观测时间0-T内物品是否成功转化,那么我们就能准确的预测出物品的CVR。
包含物品是否成功转化标签的损失函数为:
式子很好理解,不多赘述。作者在论文中证明了该式子等价于 \(L_{oracle}\) 。
那么现在问题来到了“该如何预测当前物品是否成功转化?”。由于物品是否真实转化的标签我们无法获得,所以作者采用了构造的“反事实”样本来训练子网络,从而预测样本最终是否成功转化。
本文称之为的“反事实”样本,说白了就是将现有0-T的观测数据再划分成两部分,即 counterfactual deadline (CD) 以及 actual deadline (AD) 。两者之间的gap记为 \(\tau\),这在文中是个超参数。如此我们就可以将 CD-AD 时间间隔内被转化的物品数据,视作为0-T时间内点击并成功转化的物品,其余视为物品。
如此,网络就可以设计如下:
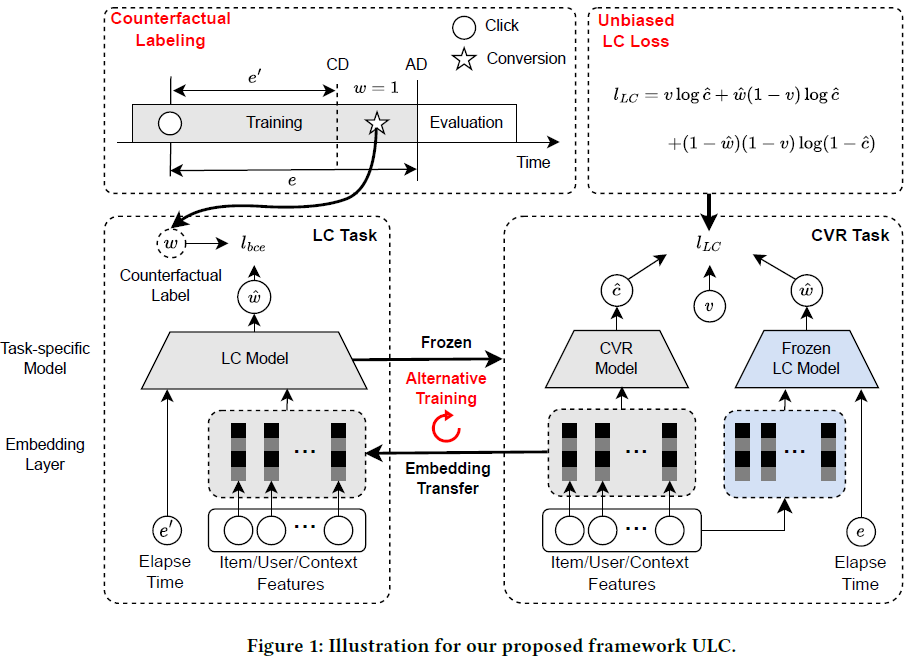
作者在文中分析,他们的方法存在两个问题:
- 产生的 conterfactual data 由于是整体数据的一个子集,所以可能使模型在学习时陷入局部最优
- 作者设计的 LC model 仍然存在反馈延迟的bias,因为未在 CD-AD 内成功转化的样本的真实标签 \(c_{i}\) 有可能是1,即最终会转化成功
对第一个问题,作者通过使 LC model 的 embedding 层与CVR model 交替更新的方式,获得所有数据的非局部最优的表征。
对第二个问题,作者说会在未来的工作中尝试解决。
方法的伪代码:




