PID控制
一、PID
1. P Controller
PID控制是控制学中一个很广的领域。这里首先以 P Controller 的例子讲起,首先给定一条规划好的参考轨迹线,为x轴,小车一开始在预定线路的上方,如图1所示,我们需要让小车重新行驶回预先规划的线路。
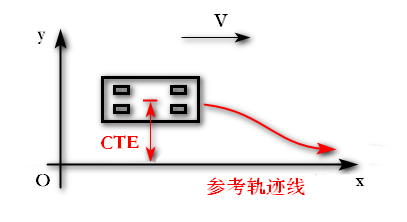
图1. CTE
转向与横切误差CTE是小车与参考轨迹线的垂直距离。因为我们参考的轨迹线是x轴,所以CTE就是小车的当前y位置。之后,通过规划线路的距离CTE获得调整的转向角度 \(\alpha\),即
\begin{equation}
\alpha = -\tau_p \cdot CTE
\end{equation}
这里的\(\tau_p\)是P Controller比例系数。然后我们调用move使得小车根据获得的转向角度开始移动。
def run(robot, tau, n=100, speed=1.0):
x_trajectory = []
y_trajectory = []
# steering = -tau * crosstrack_error
for i in range(n):
# move(self, steering, distance, tolerance=0.001, max_steering_angle=np.pi / 4.0)
crosstrack_error = robot.y - 0
steering = -tau * crosstrack_error
robot.move(steering, speed)
x_trajectory.append(robot.x)
y_trajectory.append(robot.y)
return x_trajectory, y_trajectory
robot = Robot()
robot.set(0, 1, 0) # 初始的坐标(0,1),方向角0
x_trajectory, y_trajectory = run(robot, 0.2) # tau = 0.2
最后的小车的运动曲线如图2所示。虽然小车会向参考轨迹线靠拢,但也没有预想的那样直接运行到参考线上,而是在参考线附近不停的震荡,且有失控的趋势。
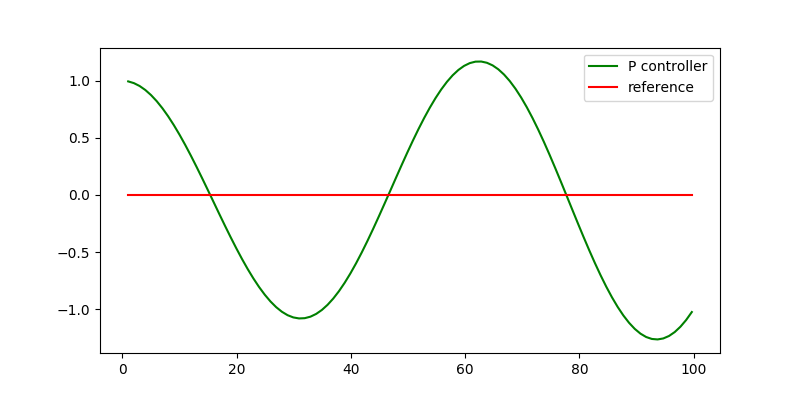
图2. P Controller
2. PD Controller
如果单使用P Controller,会导致轨迹震荡,这是因为P Controller在小车在到达指定轨迹线路时,调整的转向角度的值没有立即变为0。为了使调整的转向角度能随着\(|CTE|\)的减少而减小角度,我们可以增加一个D Controller。微分的作用主要用于克服被控对象的滞后,在温度控制系统中也经常使用。在加入D Controller的功能后, \(\alpha\)的表达式如下
\begin{equation}
\alpha = -\tau_p \cdot CTE - \tau_d \frac{d}{dt} CTE
\end{equation}
这里的$\tau_d $是D Controller比例系数。然后我们调用move使得小车根据获得的转向角度开始移动。
# steering = -tau_p * CTE - tau_d * diff_CTE
# where differential crosstrack error (diff_CTE)
# is given by CTE(t) - CTE(t-1)
def run(robot, tau_p, tau_d, n=100, speed=1.0):
x_trajectory = []
y_trajectory = []
pre_cte = robot.y
for i in range(n):
cte = robot.y
diff_CTE = cte - pre_cte
pre_cte = robot.y
steer = -tau_p * cte - tau_d * diff_CTE
robot.move(steer, speed)
x_trajectory.append(robot.x)
y_trajectory.append(robot.y)
return x_trajectory, y_trajectory
robot = Robot()
robot.set(0, 1, 0) # 初始的坐标(0,1),方向角0
x_trajectory, y_trajectory = run(robot, 0.2, 3.0) # tau_p = 0.2 , tau_d = 3.0
最后的小车的运动曲线如图3所示。小车很快调整到规划的线路,且消除了震荡。
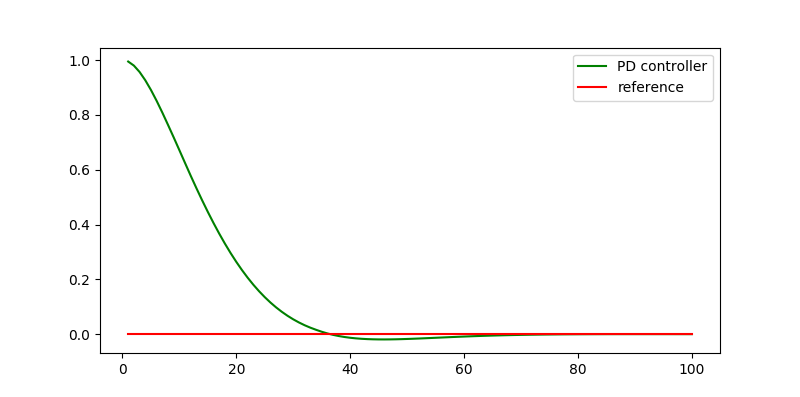
图3. PD Controller
3. PID Controller
在现实的系统中,总会有一些意料之外的系统偏差引入,这部分累计误差的消除可以借助 I Controller。积分的作用主要用于消除自动控制系统的剩余误差,在加入 I Controller的功能后, \(\alpha\)的表达式如下
\begin{equation}
\alpha = -\tau_p \cdot CTE - \tau_d \frac{d}{dt} CTE - \tau_i \sum CTE
\end{equation}
这里的\(\tau_i\)是 I Controller比例系数。然后我们调用move使得小车根据获得的转向角度开始移动。
# steering = -tau_p * CTE - tau_d * diff_CTE - tau_i * int_CTE
def run(robot, tau_p, tau_d, tau_i, n=100, speed=1.0):
x_trajectory = []
y_trajectory = []
# TODO: your code here
pre_cte =robot.y
int_CTE = 0
for i in range(n):
CTE = robot.y
diff_CTE = CTE - pre_cte
pre_cte = CTE
int_CTE += CTE
steering = -tau_p * CTE - tau_d * diff_CTE - tau_i * int_CTE
robot.move(steering, speed)
x_trajectory.append(robot.x)
y_trajectory.append(robot.y)
return x_trajectory, y_trajectory
robot = Robot()
robot.set(0, 1, 0) # 初始的坐标(0,1),方向角0
robot.set_steering_drift(10.0/180.0*np.pi) # 设定系统偏差
x_trajectory, y_trajectory = run(robot, 0.2, 3.0, 0.008) # tau_p = 0.2 , tau_d = 3.0 , tau_d = 0.008
最后的小车的运动曲线如图4所示。小车虽然一开始因为系统偏差导致越界,但是随着时间的累积,积分项会纠正系统误差。而积分项的加入会增加系统控制的鲁棒性。
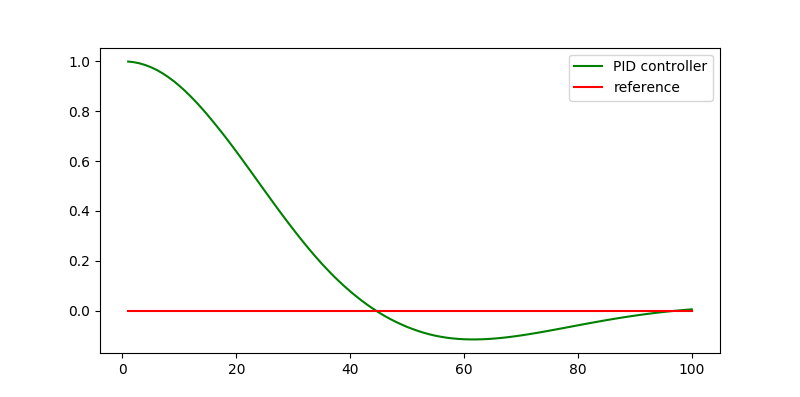
图4. PID Controller
二、Twiddle算法
Twiddle算法是一种局部爬山算法,其通过遍历\(\tau_p\),\(\tau_i\),\(\tau_d\)所有可能值,以获得较优的结果,这降低了PID调参的难度。
def twiddle(tol=0.2):
# Don't forget to call `make_robot` before every call of `run`!
p = [0, 0, 0]
dp = [1, 1, 1]
robot = make_robot()
x_trajectory, y_trajectory, best_err = run(robot, p)
# twiddle loop here
it = 0
while(sum(dp) > tol):
print("Iteration {}, best error = {}".format(it, best_err))
for i in range(len(p)):
p[i] += dp[i]
robot = make_robot()
x_trajectory, y_trajectory, err = run(robot, p)
if err < best_err:
best_err = err
dp[i] *= 1.1
else:
p[i] -= 2 * dp[i]
robot = make_robot()
x_trajectory, y_trajectory, err = run(robot, p)
if err < best_err:
best_err = err
dp[i] *= 1.1
else:
p[i] += dp[i]
dp[i] *= 0.9
it += 1
return p, best_err
params, err = twiddle()
twiddle算法与其他控制器的区别比较,如图5所示。
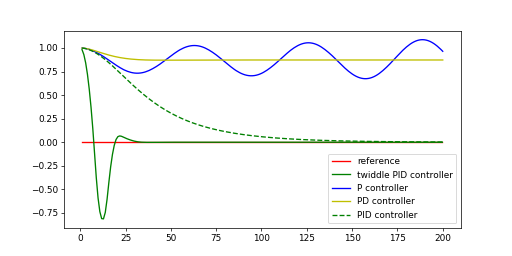
图5. 控制器比较图
三、调参体验
3.1 口诀
业界有个整定口诀:参数整定找最佳, 从小到大顺序查。先是比例后积分, 最后再把微分加。曲线振荡很频繁, 比例度盘要放大。曲线漂浮绕大弯, 比例度盘往小扳。曲线偏离回复慢, 积分时间往下降。曲线波动周期长, 积分时间再加长。曲线振荡频率快, 先把微分降下来。动差大来波动慢, 微分时间应加长。理想曲线两个波, 前高后低四比一。一看二调多分析, 调节质量不会低。
整定步骤:先比例,后积分,再微分。
3.2 实例
经验凑试法在实践中最为实用。在调节参数时,必须认真观察系统响应情况,根据系统的响应情况决定调整那些参数。 以小车为例,首先调节\(\tau_p\),因为\(\tau_p\)与问题建立线性关系,所以\(\tau_p\)越大,响应越快。然后考虑怎么用积分项消除系统的偏差。最后再调节\(\tau_d\),以此来减小系统震荡。
- 起初,我将所有PID系数设置为0.01。
- 首先,我保持I和D的系数不变,只调整了P的参数,发现当P=1.5时,相对较好。
- 之后,我调整了D的参数,发现当D =6时,它是比较好的,我可以跑很长的距离。
- 最后,保持D的参数不变,调整P的参数,当P=0.25时,顺利跑完整个路程。
P = 0.25, I = 0.01, D = 6