定位(粒子滤波)

一、粒子滤波

1.1 介绍

粒子滤波器是一种基于蒙特卡罗的近似解法，由于计算机计算能力的不断提高和易于实现，粒子滤波器在机器人定位领域得到了广泛的应用，其优势在于对复杂问题的求解上，比如一些非线性、非高斯动态系统的状态递推估计或概率推理问题。粒子滤波器的本质是使用一组有限的加权随机样本（粒子）来近似表征任意状态的后验概率密度 \(bel(x_t)\) 。

1.2 算法

粒子滤波器的算法流程主要是对粒子集\(X\)的预测和更新。

该算法的输入是粒子集\(X_{t-1}\)，以及最新的控制\(u_t\)和测量\(z_t\)。算法首先构造一个暂时的粒子集 \(\bar{X}\)，表示置信度 \(\bar {bel(x_t)}\)。这通过系统地处理输入粒子集\(X_{t-1}\)中的每个粒子\(x^{[1]}_{t-1}\)完成。随后它将这些粒子转换为粒子集\(X_t\)，用于近似后验分布 \(bel(x_t)\)。值得注意的是，这里 \(M\) 代表粒子集\(X_t\)的粒子数量，\(M\)的要根据实际情况选取合适的值。\(w^{[m]}_t=p(z_t|x^{[m]}_t)\)是测量\(z_t\)在粒子\(x^{[m]}_t\)下的概率，是粒子滤波表征后验概率密度的由来，即通过当前的观测到的数据来预测当前状态的发生概率。还有就是算法的更新部分，采用了重采样（有一个版本是不进行重采样的）。

二、定位

2.1 初始化

假定机器人是在一个二维的世界中，在这个世界中可以被感知到的路标点有4个，分别是\(L1(20.0, 20.0)\), \(L2(80.0, 80.0)\), \(L3(20.0, 80.0)\), \(L4(80.0, 20.0)\)，同时地图的大小是100X100。那么首先我们在地图上随机一个机器人的坐标(x,y)和运动方向orientation，设定粒子集的M为1000，每个粒子都初始化一个和机器人相同数据结构的状态。

N = 1000 #初始粒子个数
p = [] #粒子集
world_size = 100.0 #地图尺寸

for i in range(N):
    x = random.random() * world_size
    y = random.random() * world_size
    orientation = random.random() * 2.0 * pi
    p.append([x,y,orientation])

接着给机器人设定初始噪声参数，分别是前进噪声\(forward_{noise}\)，转向噪声\(turn_{noise}\)和传感器噪声 \(sense_{noise}\)。

forward_noise = 5.0
turn_noise = 0.1
sense_noise = 5.0

2.2 预测

对每一个粒子根据机器人的运动状态，进行下一个状态的预测，例如，机器人的运动指令是先顺时针转动pi/2，再前进10米，则所有的粒子都采用相同的运动指令。

myrobot = myrobot.move(-pi/2, 10.0) #机器人先顺时针转动pi/2，再前进10米

p2 = [] #粒子和机器人做出同样的动作
for i in range(N):
    p2.append(p[i].move(-pi/2, 10.0)) 
p = p2

接着运动之后的，机器人感知路标点，获得与4个路标点的测量距离Z，然后那些粒子也都进行一次路标点的距离dist的计算，然后每个粒子通过各自dist和Z的相近程度，分配权值w。dist与Z越接近，权值w越大，即该粒子越可能是当前机器人的所在点。

2.3 重采样

重采样采用Resampling wheel算法。我们将所有粒子摆在轮盘上，并规定粒子权重的大小和其所占的转轮面积成正比。随后确定一个转盘指针的位置index，beta是在当前index的粒子中，可否被采样的指标。初始beta为0，每次转动转盘我们随机增加r给beta。在重采样中会出现两种情况：

• 当\(beta > w[index]\)时，此时算没有抽中，我们将index更新为index+1，同时beta更新为beta-w[index]。
• 当\(beta \leqslant w[index]\)时，此时算抽中， 将编号为index的粒子采样到新的粒子集中，之后转动转盘接着抽，且beta更新为beta+r，直到beta的值大于index所指的权重。

p3 = []
index = int(random.random()*N) # 从N个粒子中随机选择一个粒子的编号index
beta = 0.0
mw = max(w) #获取粒子集中最大一个粒子的权值w
for i in range(N):
    r = random.random() * 2.0 * mw 
    beta += r
    while beta > w[index]:
        beta -= w[index]
        index = (index + 1) % N
    p3.append(p[index])

2.4 结果

最终，经过不断的预测，重采样更新粒子集，把那些和机器人有着相似观测数据的粒子保留了下来。之后我们可能将权值最大的粒子的状态当作此时机器人的状态，完成了定位。粒子滤波定位的演示如下，绿色是机器人，红色是粒子，一开始这些粒子是均匀分布在地图的，随着机器人的不断运动，慢慢只剩下符合机器人状态的粒子。

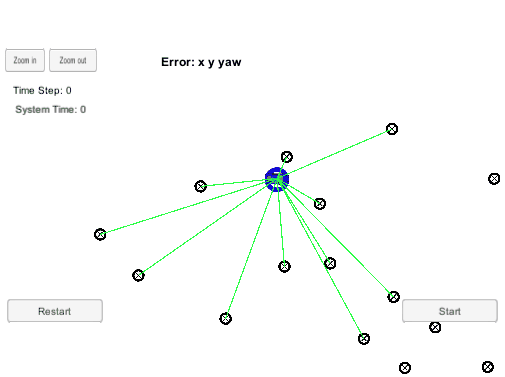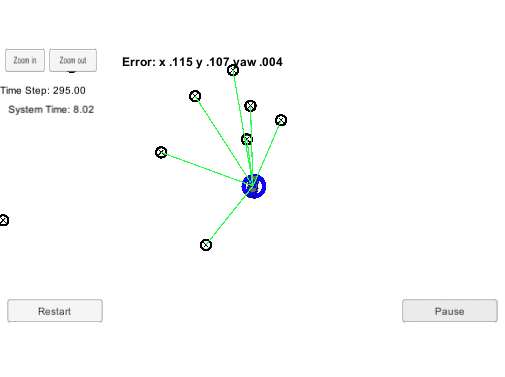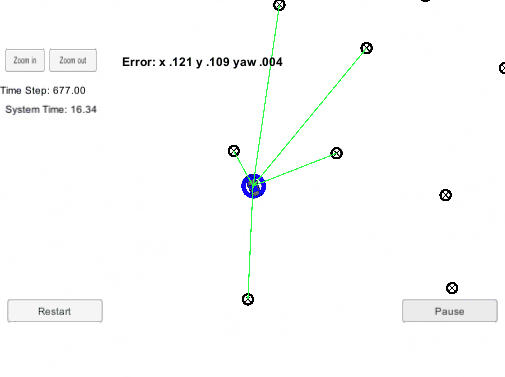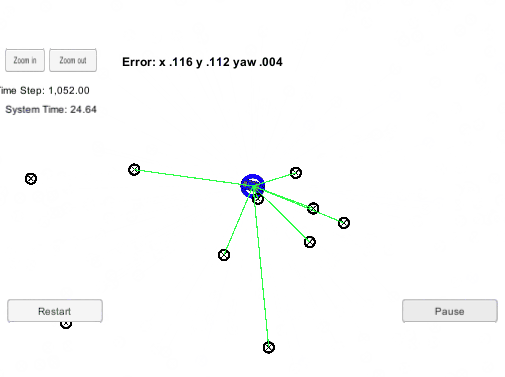
图2. 粒子滤波demo