CF460D Little Victor and Set (找规律)
Codeforces Round #262 (Div. 2) D
|
D. Little Victor and Set
time limit per test
1 secondmemory limit per test
256 megabytesinput
standard inputoutput
standard outputLittle Victor adores the sets theory. Let us remind you that a set is a group of numbers where all numbers are pairwise distinct. Today Victor wants to find a set of integers S that has the following properties:
Help Victor find the described set. Input
The first line contains three space-separated integers l, r, k (1 ≤ l ≤ r ≤ 1012; 1 ≤ k ≤ min(106, r - l + 1)). Output
Print the minimum possible value of f(S). Then print the cardinality of set |S|. Then print the elements of the set in any order. If there are multiple optimal sets, you can print any of them. Sample test(s)
Input
8 15 3 Output
1 Input
8 30 7 Output
0 Note
Operation |
题意:给出l,r,k,要从[l,r]中的数选出最多k个组成集合,使这些元素异或起来得到的结果最小,输出最小值和这些元素,若多解输出任意满足条件的解。
题解:分析,找到规律然后搞。
题目要求异或得的值尽量小,所以我们研究如何能异或得到小值。
可以发现如下规律:
1. 一个偶数和 它本身加一 异或,得1。(xxxxxx0 xor xxxxxx1 = 0000001)
2. 4的倍数和它背身加1 加2 加3 一共4个数异或,得0。(...00 xor ...01 xor ...10 xor ...11=0)
由上面两个规律,当k>=4的时候,我们找区间内有没有完整的4的倍数x, x+1, x+2, x+3,若有,则直接得0。若没有,则区间内元素个数肯定小于6,直接2^6暴力得到最优解。
若k==1,则直接返回l。
如k==2,则区间元素个数只要大于等于3,肯定能得1。两个不同的元素不可能异或得0,只有相同的两个才能异或得0,所以k==2最少也就是1了。如果区间只有l和r两个元素,l还是奇数,那就得不了1,最小异或结果就是min( l , l^r),也就是单独L一个不异或和l异或r中比较小的。
然后就是比较难想的,k==3的情况了。
k==3是可以异或得到0的,这个情况也比较特殊,因为三个1异或是会得1的,所以不可能像上面连续找好几个数异或得0,因为连续的数高位是一样的,都是1的话就会异或得1。
所以我们要找的三个数,每位上需要有2个1或者0个1。像上面一样,我们尽量找接近的数,这样比较容易在区间中找到。
110000000
101111111
011111111
看这三个异或结果为0的二进制数,很接近了。如果区间内有3个数能异或成0,区间内肯定能找到形式为这样的3个数异或为0。具体证明比较复杂,我脑内反证了很久……我就不详细写了。
然后我们根据这个,知道l和r的二进制位数必须不一样才能组成这样的3个数(位数一样的话最高位都是1,肯定不能得0),我们可以用l的二进制位数来试一试,不行的话用l的位数加一试一试,就是看看这样构造出来的三个数是不是都在区间内。如果这两种位数都不行的话就不行了,行的话肯定在这两种位数里有答案。
k==3这部分的代码:
1 if(k==3) { 2 int lwei,rwei; 3 lwei=0; 4 rwei=0; 5 ll t=l; 6 while(t)t>>=1,lwei++; 7 t=r; 8 while(t)t>>=1,rwei++; 9 if(rwei>=2 && lwei<rwei) { 10 ll q[3]; 11 for(i=lwei+1-2; i<=lwei+2-2; i++){ 12 q[0]=(3LL<<i); 13 q[1]=q[0]-1; 14 q[2]=(1LL<<(i+1))-1; 15 bool dou=0; 16 for(int j=0;j<3;j++) 17 if(q[j]<l || q[j]>r){dou=1;break;} 18 if(dou)continue; 19 v.pb(q[0]); 20 v.pb(q[1]); 21 v.pb(q[2]); 22 return 0; 23 } 24 } 25 }
全代码:

1 //#pragma comment(linker, "/STACK:102400000,102400000") 2 #include<cstdio> 3 #include<cmath> 4 #include<iostream> 5 #include<cstring> 6 #include<algorithm> 7 #include<cmath> 8 #include<map> 9 #include<set> 10 #include<stack> 11 #include<queue> 12 using namespace std; 13 #define ll long long 14 #define usll unsigned ll 15 #define mz(array) memset(array, 0, sizeof(array)) 16 #define minf(array) memset(array, 0x3f, sizeof(array)) 17 #define REP(i,n) for(i=0;i<(n);i++) 18 #define FOR(i,x,n) for(i=(x);i<=(n);i++) 19 #define RD(x) scanf("%d",&x) 20 #define RD2(x,y) scanf("%d%d",&x,&y) 21 #define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z) 22 #define WN(x) prllf("%d\n",x); 23 #define RE freopen("D.in","r",stdin) 24 #define WE freopen("1biao.out","w",stdout) 25 #define mp make_pair 26 #define pb push_back 27 28 ll l,r,k; 29 vector<ll>v; 30 31 ll b[10],bn; 32 ll c[10],cn,miny; 33 void dfs(ll x,ll y,int cnt) { 34 if(cnt>k)return; 35 if(x>r) { 36 if(cnt!=0 && y<miny) { 37 cn=bn; 38 int i; 39 REP(i,bn)c[i]=b[i]; 40 miny=y; 41 } 42 return; 43 } 44 b[bn++]=x; 45 dfs(x+1,y^x,cnt+1); 46 bn--; 47 dfs(x+1,y,cnt); 48 } 49 50 ll farm() { 51 ll i; 52 v.clear(); 53 if(k==1) { 54 v.pb(l); 55 return l; 56 } 57 58 if(k>=4) { 59 ll wa=(ll)(l/4)*4; 60 while(wa<l)wa+=4; 61 if(wa+3<=r) { 62 v.pb(wa); 63 v.pb(wa+1); 64 v.pb(wa+2); 65 v.pb(wa+3); 66 return 0; 67 } 68 bn=0; 69 miny=1LL<<60; 70 dfs(l,0,0); 71 REP(i,cn)v.pb(c[i]); 72 return miny; 73 } 74 75 if(k==3) { 76 int lwei,rwei; 77 lwei=0; 78 rwei=0; 79 ll t=l; 80 while(t)t>>=1,lwei++; 81 t=r; 82 while(t)t>>=1,rwei++; 83 if(rwei>=2 && lwei<rwei) { 84 ll q[3]; 85 for(i=lwei+1-2; i<=lwei+2-2; i++){ 86 q[0]=(3LL<<i); 87 q[1]=q[0]-1; 88 q[2]=(1LL<<(i+1))-1; 89 bool dou=0; 90 for(int j=0;j<3;j++) 91 if(q[j]<l || q[j]>r){dou=1;break;} 92 if(dou)continue; 93 v.pb(q[0]); 94 v.pb(q[1]); 95 v.pb(q[2]); 96 return 0; 97 } 98 } 99 } 100 101 if(l==1) { 102 v.pb(1); 103 return 1; 104 } 105 106 ll wa=((ll)((l+1)/2))*2; 107 if(wa>=l && wa+1<=r){ 108 v.pb(wa); 109 v.pb(wa+1); 110 return 1; 111 }///区间内元素大于3的话肯定行,不然区间内只有l和r两个元素 112 113 if(l< (l^r)){ 114 v.pb(l); 115 return l; 116 }else{ 117 v.pb(l); 118 v.pb(r); 119 return l^r; 120 } 121 } 122 123 int main() { 124 ll i; 125 scanf("%I64d%I64d%I64d",&l,&r,&k); 126 ll ans=farm(); 127 printf("%I64d\n",ans); 128 ll maxi=v.size(); 129 printf("%I64d\n",maxi); 130 if(maxi>0)printf("%I64d",v[0]); 131 for(i=1; i<maxi; i++)printf(" %I64d",v[i]); 132 return 0; 133 }
这道题我觉得是有点复杂,我比赛后还WA了好多次,细节没处理好。真没法在比赛中搞出来,真难玩,日后一定要碉。


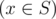 the following inequality holds
the following inequality holds 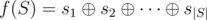 must be as small as possible.
must be as small as possible. 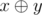 represents the operation of bitwise exclusive OR. In other words, it is the XOR operation.
represents the operation of bitwise exclusive OR. In other words, it is the XOR operation.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号