信息论——信道编码定理，反馈信道，信源信道分离，Hamming码笔记

信道编码定理

 

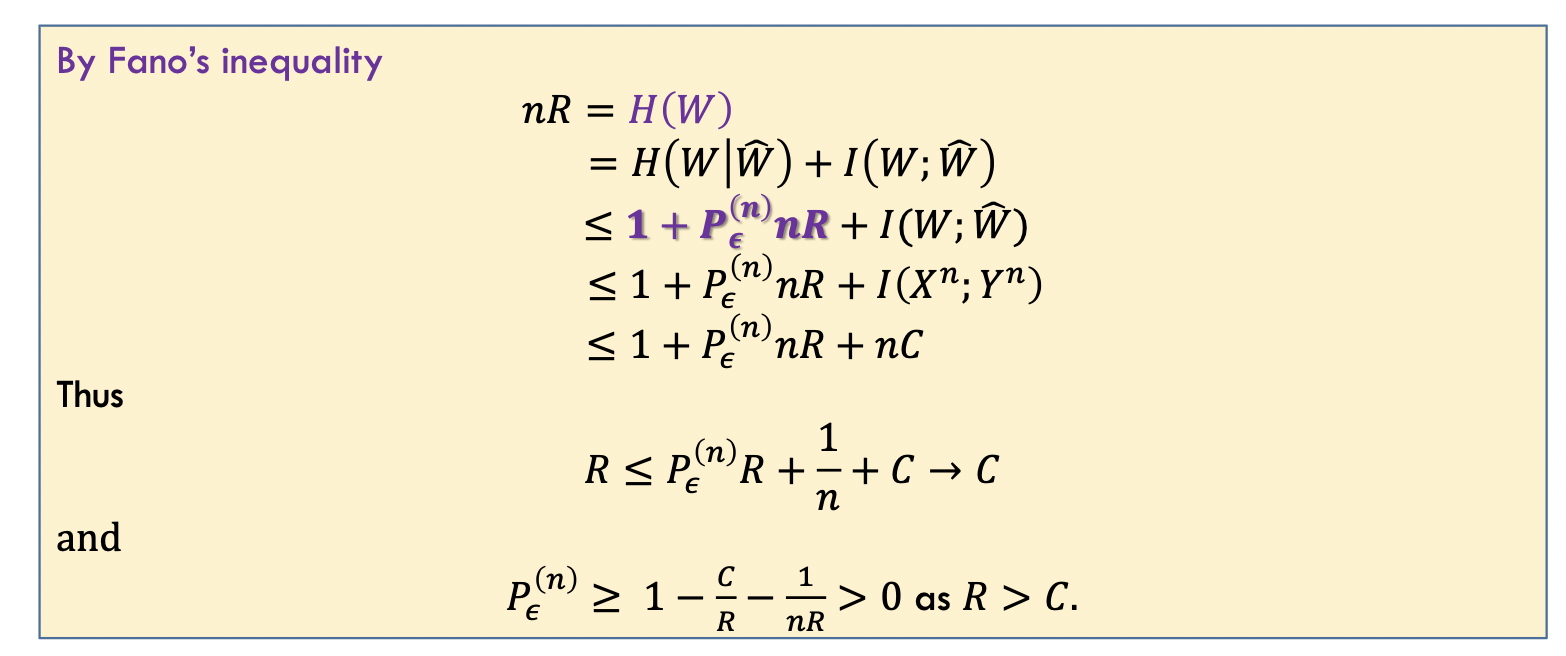
编码构建

 

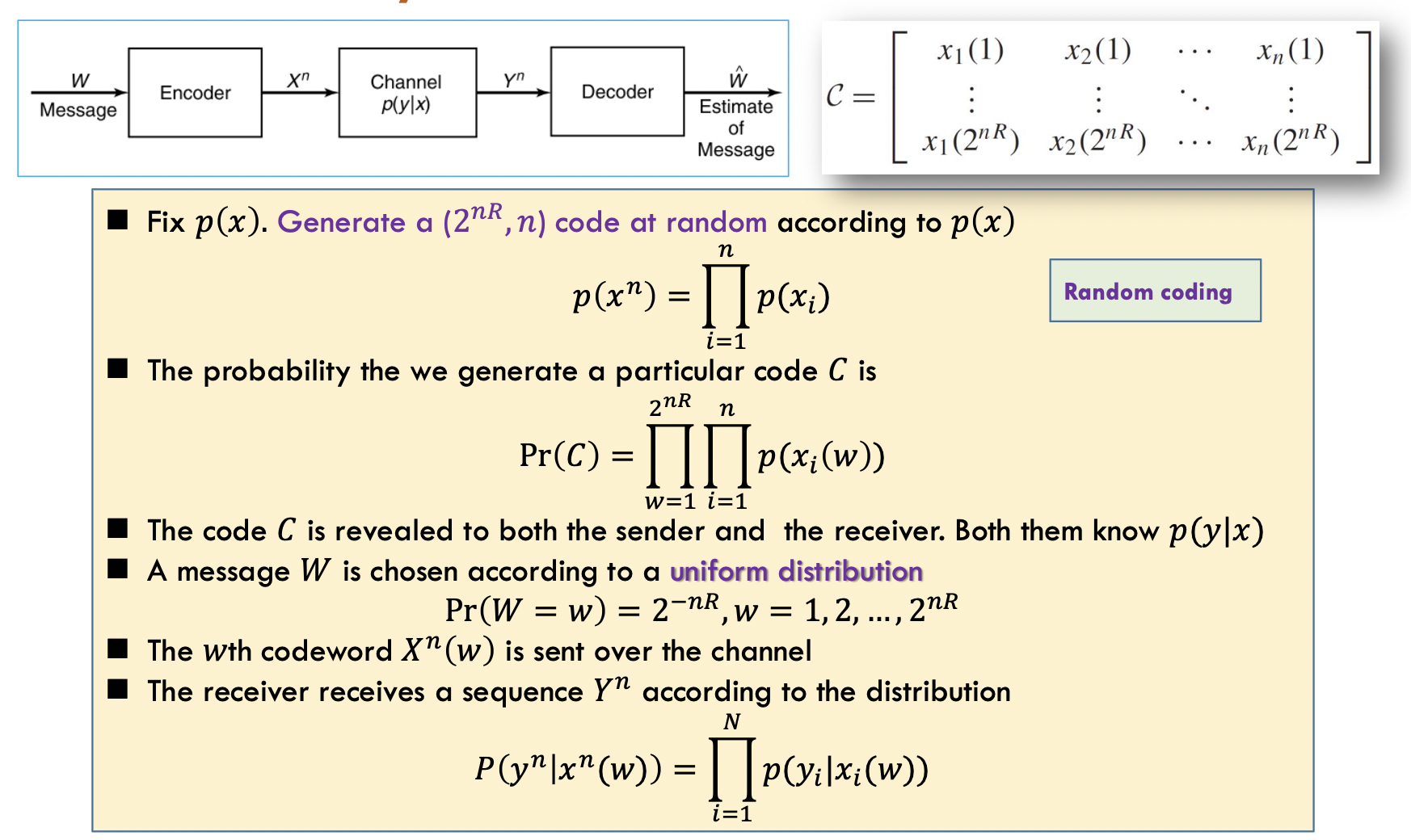
解码构建

基于联合典型集解码

 

误差估计

 

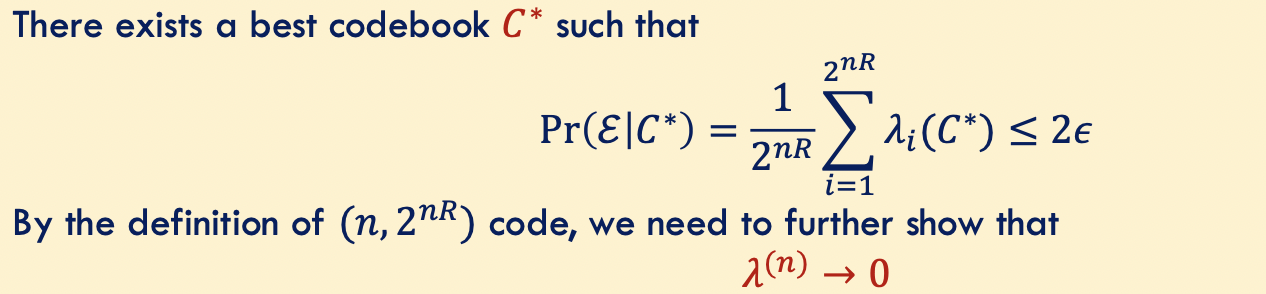
 即存在一种码本使误差趋于0

并且根据证明过程我们可以获得调整码本的方法：

 

有反馈时信道容量并不能增加

 

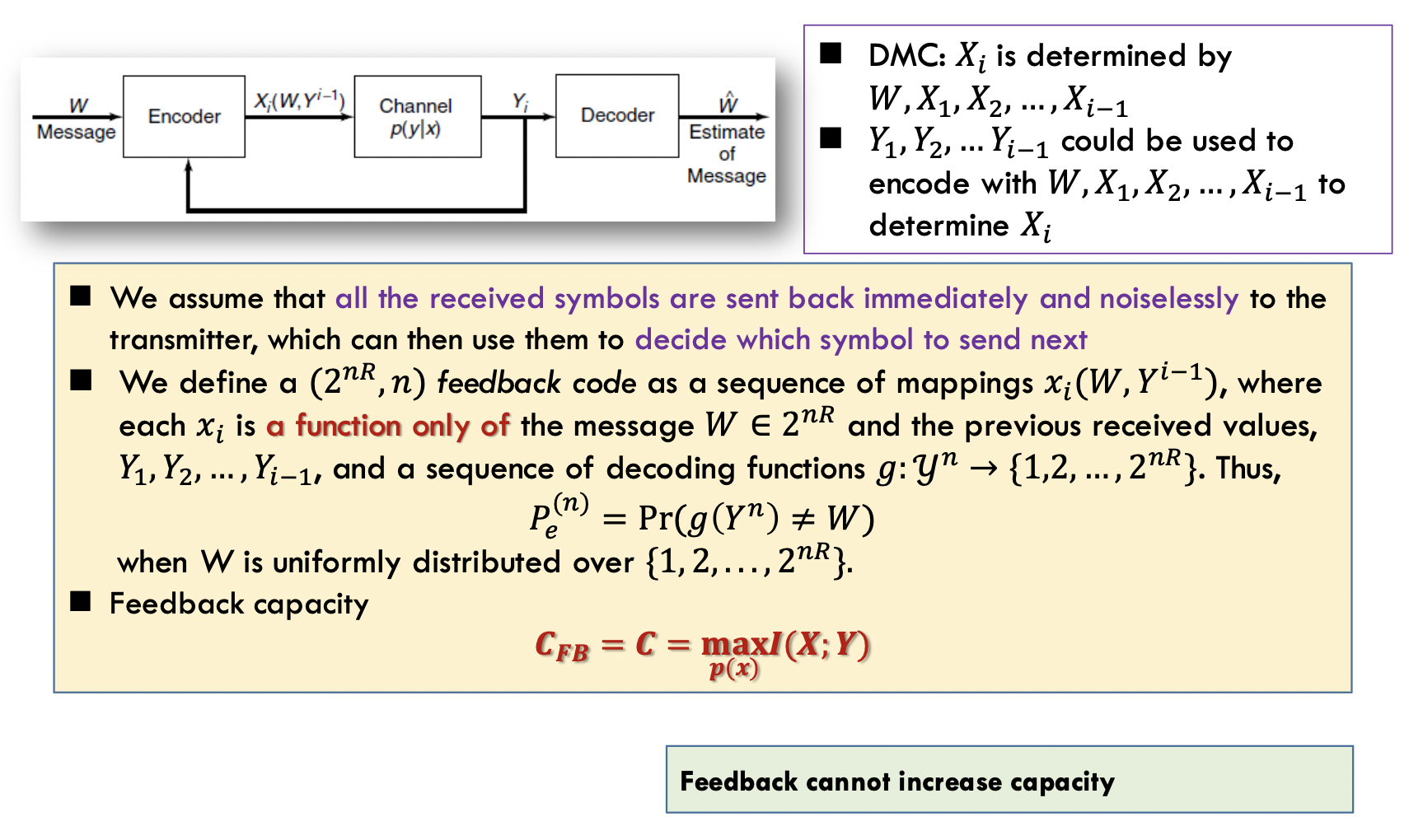
 哲学意义？

证明：

 

 

由：

 

 我们有：

信源信道独立定理

 

 

对恢复源信息的建模

最后，我们希望在丢失或发生错误的情况下也能恢复源信息，那就要给源信息增加冗余：

首先我们建模：对于一种传输方案X->Y，我们把发生错误的概率刻画为对每个信息x->y的改变量，记为d（x , y），

如：

 

那么相当于对每个x，我们要在信道容量空间中放入一个半径为d（x , y）的球（这样才能保证恢复出信息）。

为了充分利用信道，我们尽量放入更多的球：

 

 

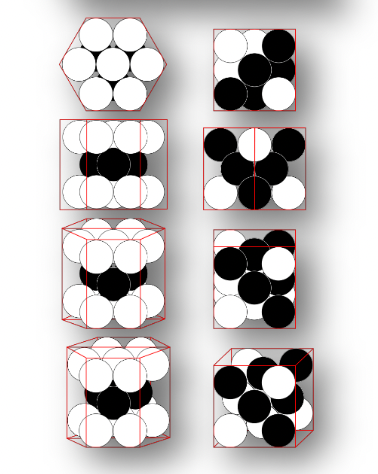
Hamming Code

 

 比如以每个园内数和mod2为0我为判断条件，如果发出左下角的信息，收到右下角的信息，那么显然可以看出哪里出现了问题。