信息论——Huffman编码、Shannon-Fano-Elias编码笔记

学到这一讲不禁再一次被信息论的魅力所征服～

同时也感到优秀的大学的课程资源确实更好，羡慕。。。

 

Huffman编码

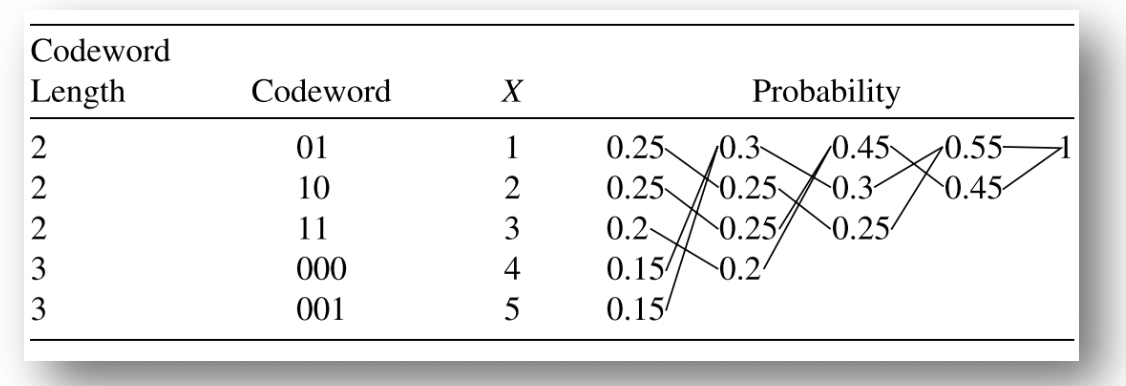
这里并不局限于两两合并，三三合并等也是可以的。

Huffman编码的平均码长是最优的。

Huffman编码的结果不唯一。

如果出现编码元素不够的情况可以增加空内容来解决：

 

由于每次合并减少（D-1）个符号，所以我们要加1+k(D-1)个空符号。

 

最优编码性质

 

 

对比Shannon编码

Shannon编码对于p都是D^(-n)是最优的。

Shannon编码的问题：当p趋于0时，编码长度过大。

 

Huffman编码最优性证明

（太强了～）

 

 

 

Shannon-Fano-Elias编码

核心：累计概率中值截取

 

 其性能仅比Huffman差一点，但是是一种全新的编码方式。

实例及性质：

上述结论表明任一种编码不可能在所有方面比Shannon-Fano-Elias编码好。

由此也能看出Shannon-Fano-Elias编码的强大。

 

最后我觉得Huffman的经历也很精彩，贴上：

Huffman的经历