信息论——近似均分性、典型集、数据压缩笔记

这一讲研究的是独立同分布的样本空间。

首先定义样本空间中某件事情的概率：

 

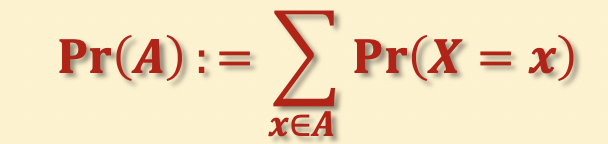
即组成成分的概率的和。（独立性使然）

 

大数定理

 

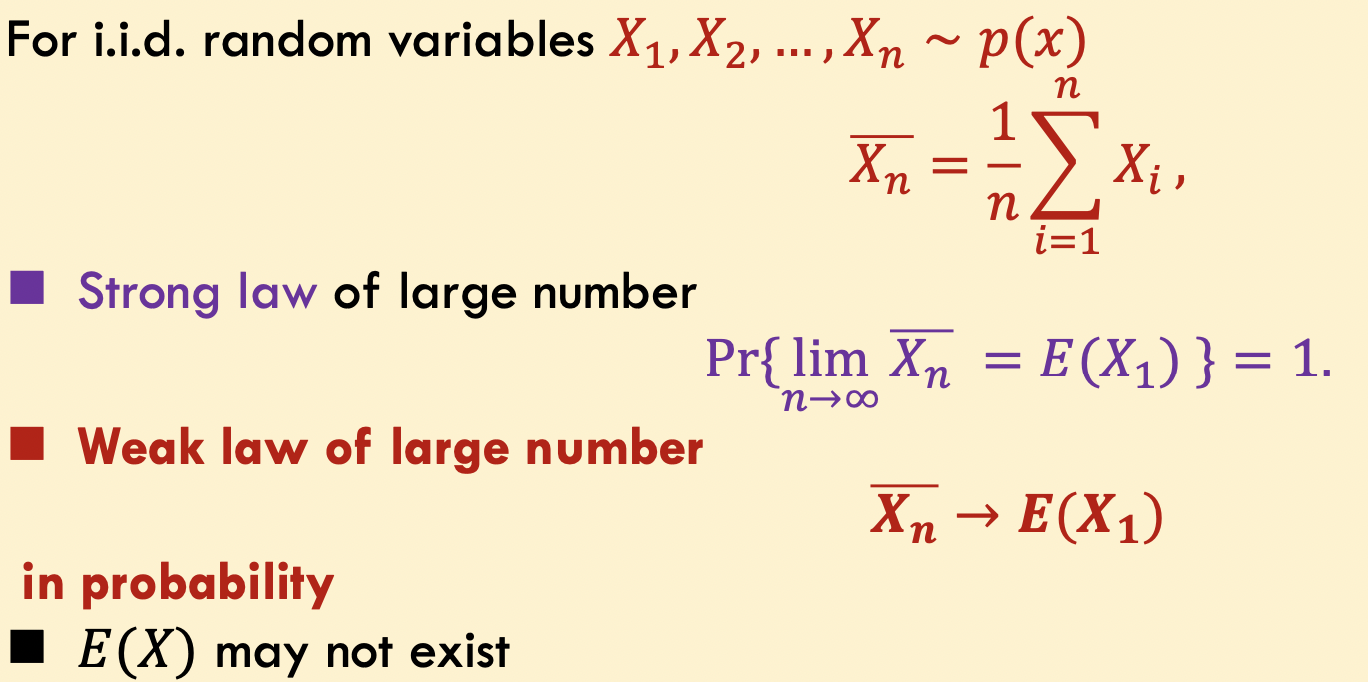
渐进均分性

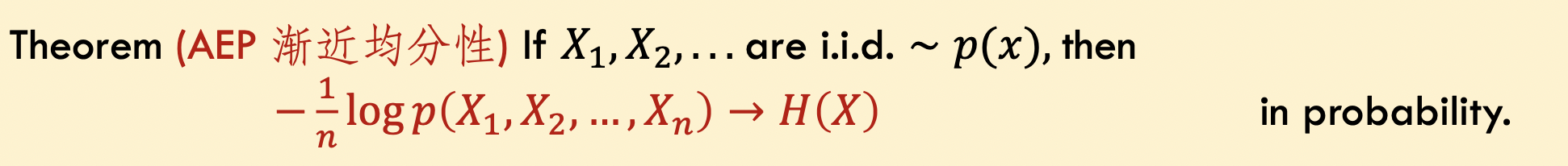
基于此，我们能推出

 

这个式子说明，n充分大时，p（X1,X2...Xn）趋于1。

于是我们可以把所有事件分为两类：概率小的和概率大的。

概率大的部分我们称为:

 

典型集

我们可以对典型集的元素个数估计：

 

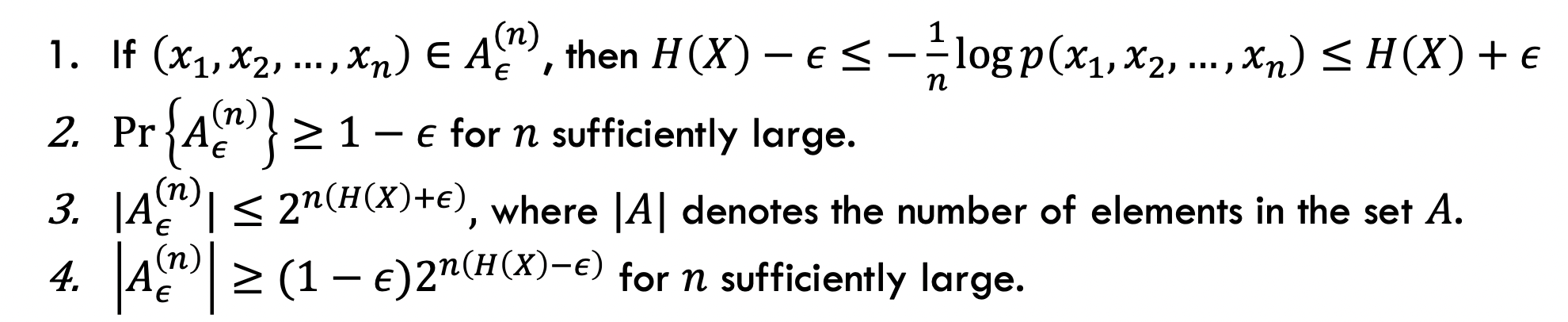
 其中3、4的证明（经典技巧）：

 

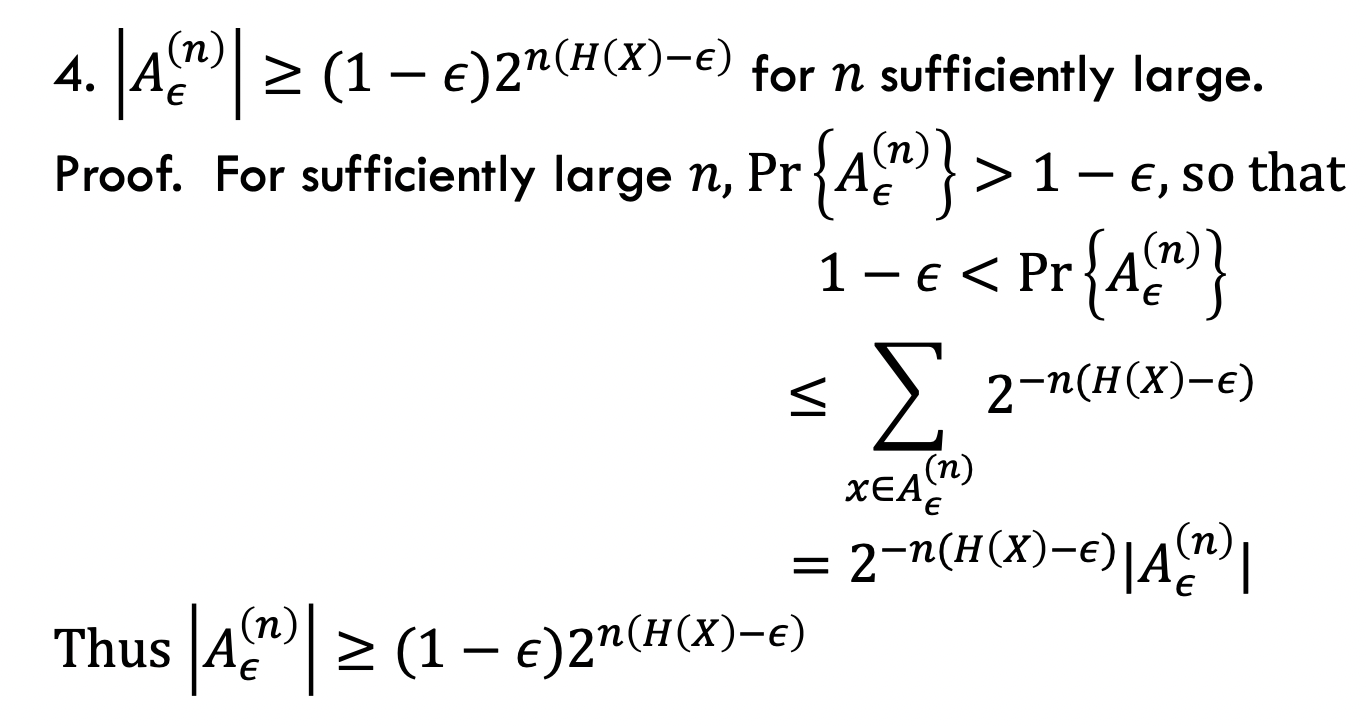
既然典型集的出现概率非常大，那么在这个样本空间里其他发生概率的事件一定跟典型集交集很多，那么其元素也会很多：

 

最后来看信源传输：

 

 

 

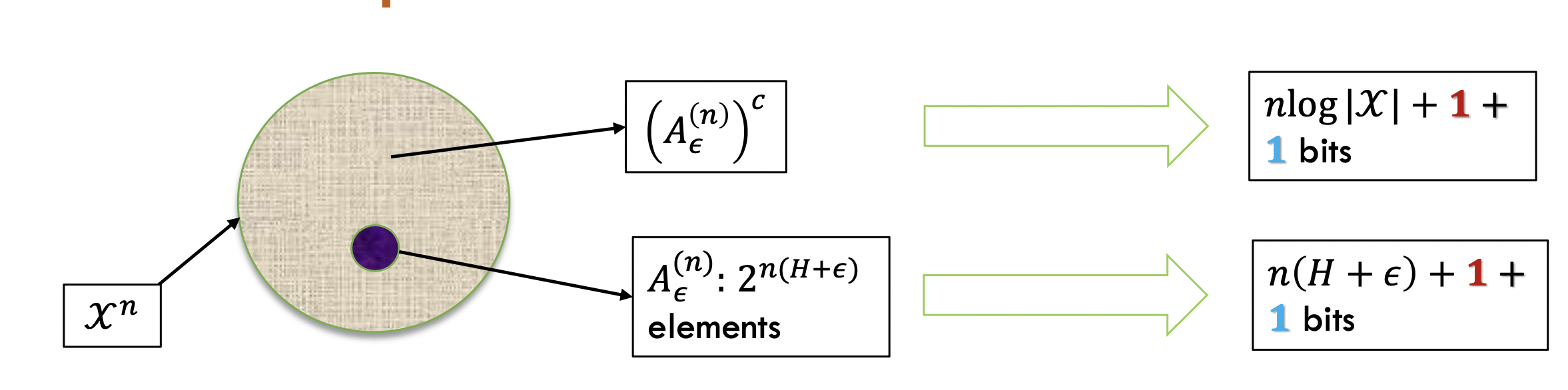
我们把样本分成两类：典型集和非典型集。

非典型集要n*log|X|+1的信息量，典型集要n*(H+e)+1的信息量（类似向上取整），然后再用1bit来分辨典型集和非典型集。

最后推出：

 

 即这种编码方式码率小于H（X）且可以在n充分大正确率趋于1。