倍道而行：二分搜索树->[搜索+查找]

二分搜索数的结构，如图：

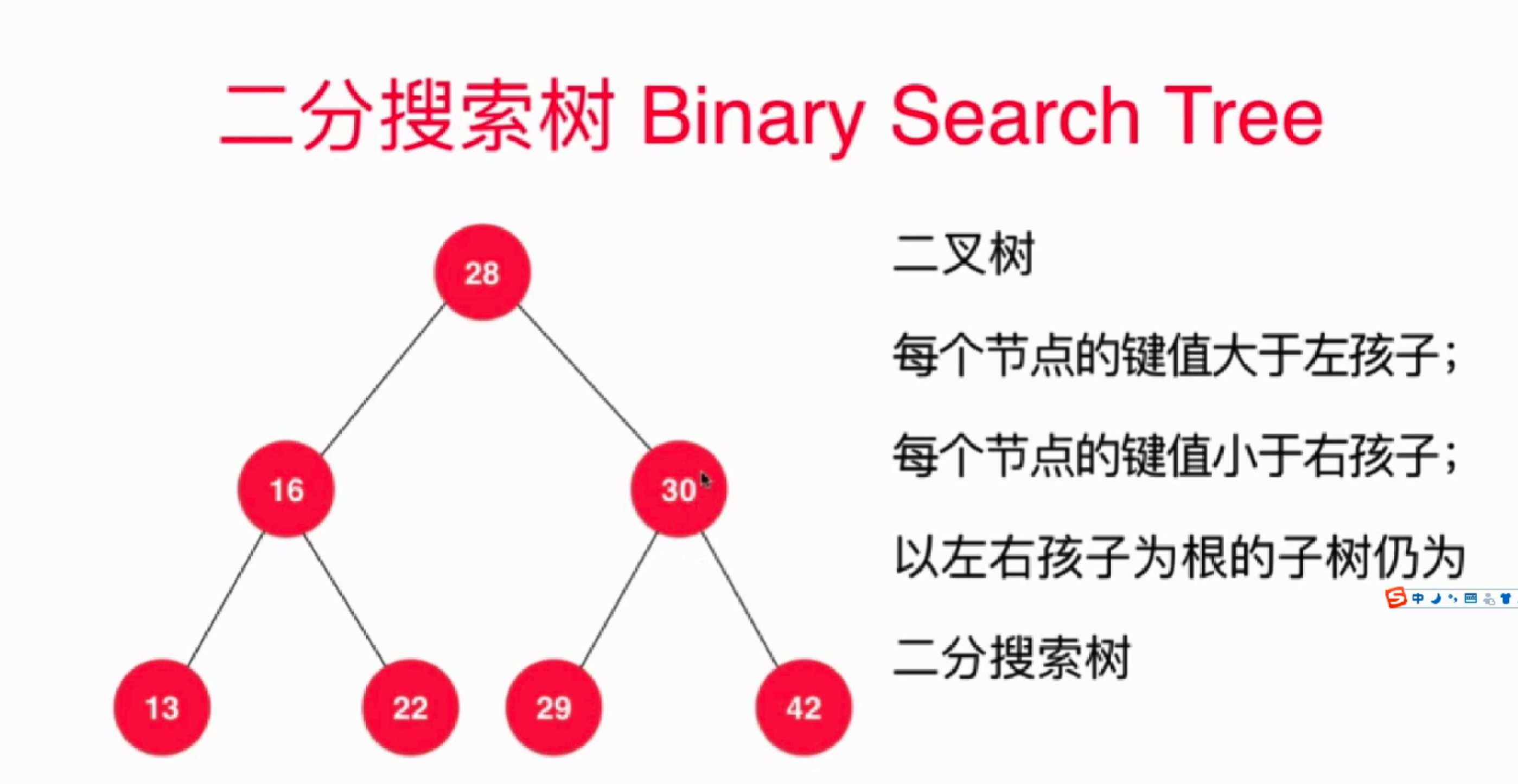
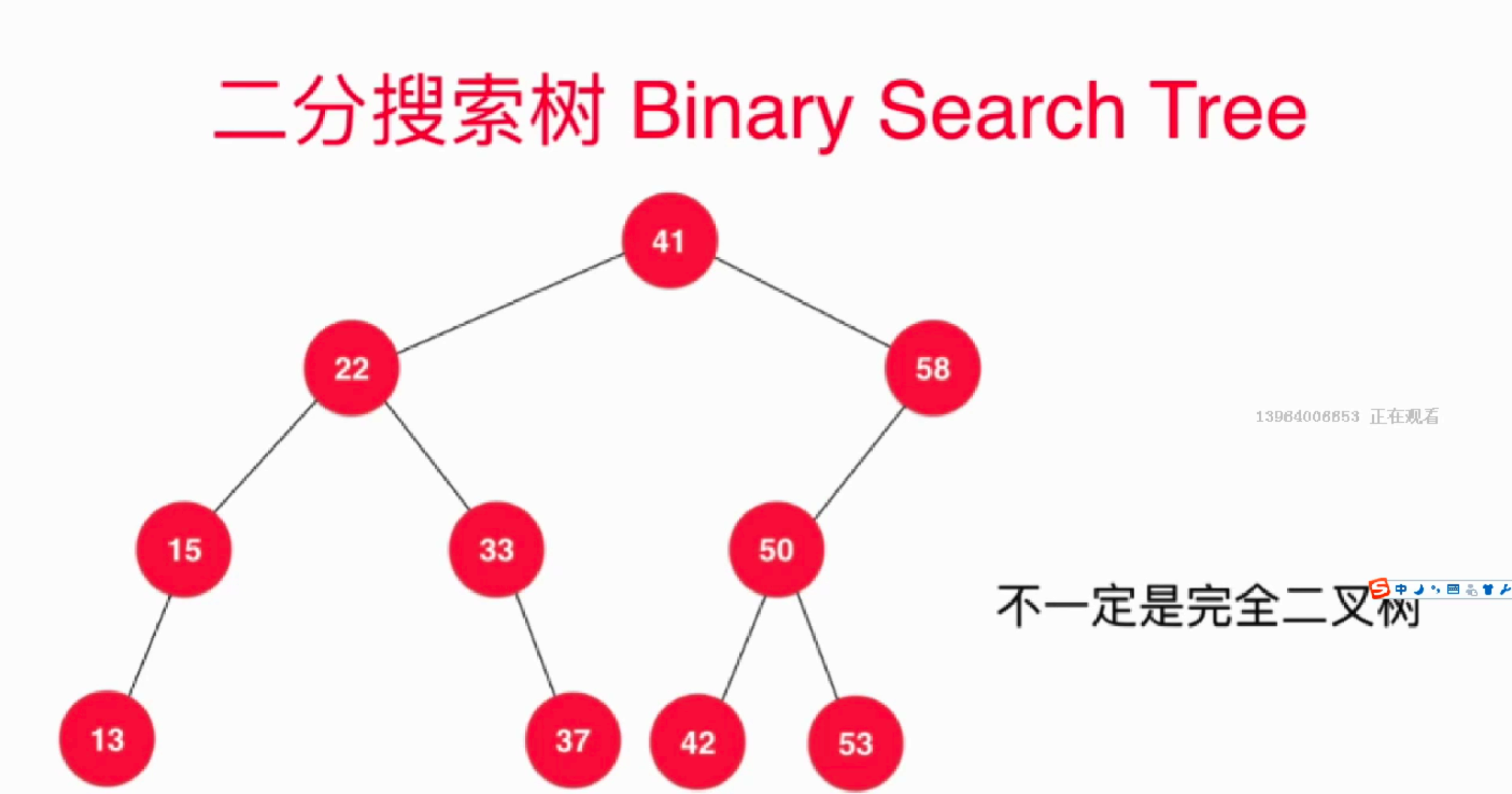
满足以上的结构即可；和之前的堆结构（完全二叉树）是不一样的。因此，二分搜索的构造是不好用数组存储的，这里用的是节点这个对象存储其键值对。

---

二分搜索树的构建（也就是插入的流程）

主要讲解下面这个递归函数：

 

Node * insert(Node *node,Key key,Value value){
        
        if (node == NULL) {
            count ++;
            return  new Node(key,value);
        }
        if (node->value == key)
            node->value = key;
        else if(node->value < key)
            node->right = insert(node->right, key, value);
        else if(node->value > key)
            node->left = insert(node->left, key, value);
        
        return node;
    }

 

• 1.从根节点开始遍历，如果相同就更新value的值，
• 2. 如果 node->value < key，那么就遍历右节点，进行递归
• 3. 如果  node->value > key，那么就遍历左节点，进行递归
• 4。也就是递归结束条件，如果遍历的节点为空，就开始创建新的节点，也就是插入一个新的节点

下面是真个程序的详细代码：

//
//  main.cpp
//  二分搜索树
//
//  Created by 余辉 on 2018/3/19.
//  Copyright © 2018年 余辉. All rights reserved.
//

#include <iostream>
using namespace std;

template <typename Key, typename Value>
class BST{
    
private:
    struct Node{
        Key key;
        Value value;
        Node * left;
        Node * right;
        
        Node(Key key, Value value){
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
        }
    };
    
    Node *root;
    int count;
    
public:
    BST(){
        root = NULL;
        count = 0;
    }
    ~BST(){
        // TODO: ~BST()
    }
    
    int size(){
        return count;
    }
    
    bool isEmpty(){
        return count == 0;
    }
    
   void insert(Key key,Value value){
       root = insert(root, key,value);
    }
private:
    Node * insert(Node *node,Key key,Value value){
        
        if (node == NULL) {
            count ++;
            return  new Node(key,value);
        }
        if (node->value == key)
            node->value = key;
        else if(node->value < key)
            node->right = insert(node->right, key, value);
        else if(node->value > key)
            node->left = insert(node->left, key, value);
        
        
        return node;
    }
};

---

 

 说完插入：咱在谈谈查找：【本质和插入非常的相似】

 

    // 查看以node为根的二叉搜索树中是否包含键值为key的节点
    bool contain(Node* node, Key key){

        if( node == NULL )
            return false;

        if( key == node->key )
            return true;
        else if( key < node->key )
            return contain( node->left , key );
        else // key > node->key
            return contain( node->right , key );
    }

 

 

这也是一个递归函数，如果包含就返回true,都则返回false【也是递归结束的条件】。

本质和insert函数很相似。

整个实现的核心：就是二叉树的构造性质，父节点的键值大于左孩子但是小于右孩子。