【研究生学习】深度学习中几种常用的卷积形式的原理以及其Pytorch调用

本篇博客主要记录一下在深度学习中几种常用的卷积形式的基本原理、输入输出维度，以及如何在Pytorch中实现这些卷积

普通卷积

卷积实际上是对图像的不同区域进行特征提取，一般认为输入图像的维度为H×W×C，如下图所示：

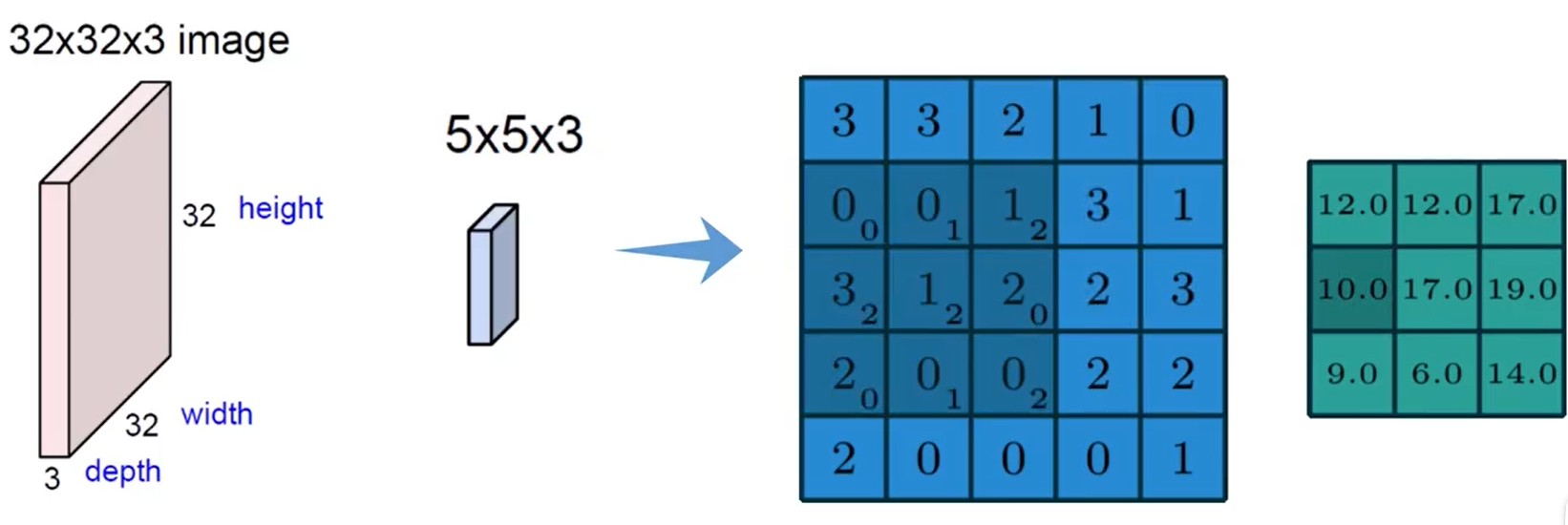
图像具有颜色通道，一般是RGB，需要理解的是不同通道数的图像和不同的通道数的滤波器如何计算得到结果，通过下面的图比较直观的理解：

可见图像中的通道数C与滤波器中的通道数要保持一致
同时需要进行滑动来计算下一个值：

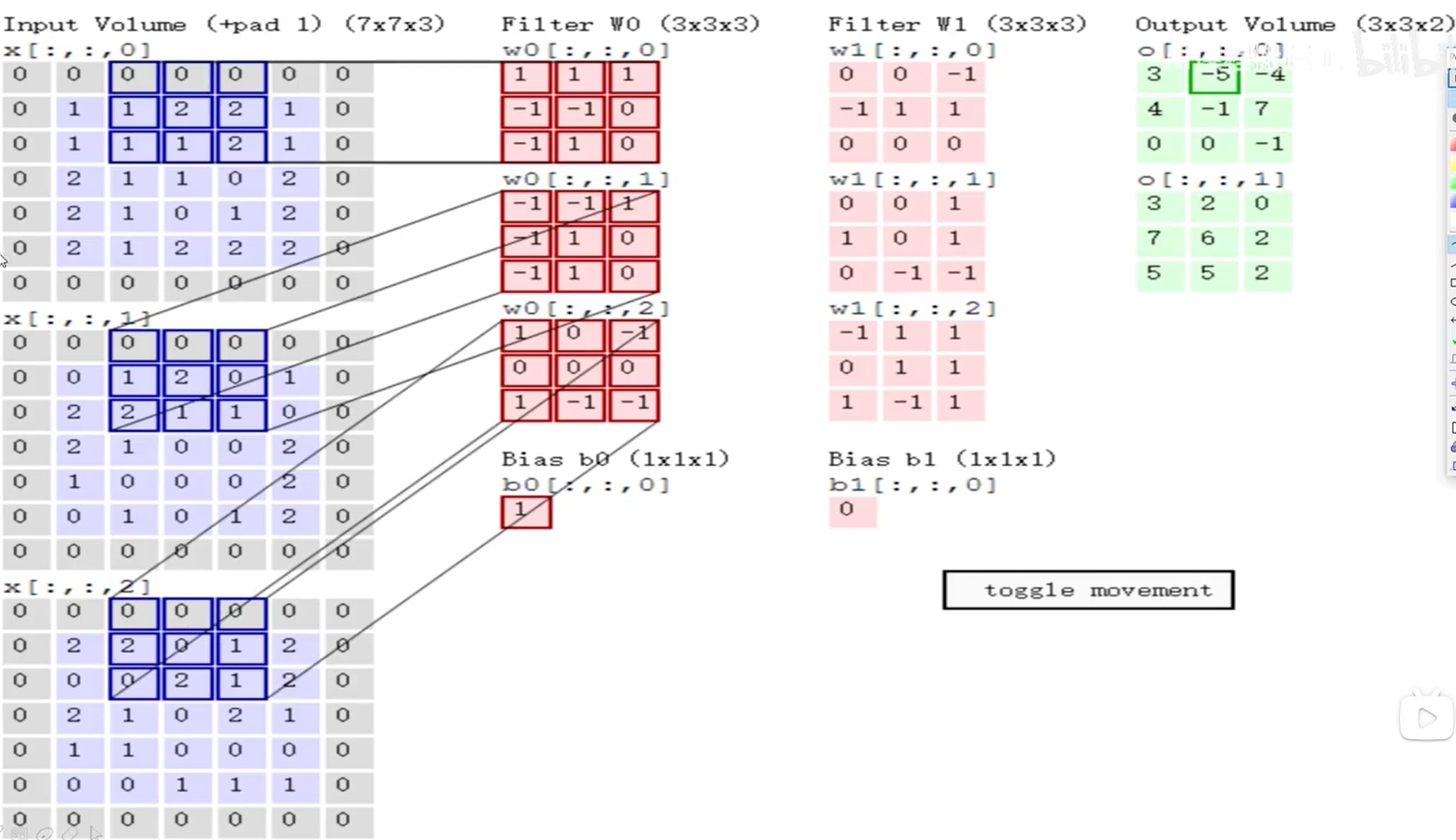
可见卷积层中设计的参数如下：
（1） 滑动窗口步长
（2） 卷积核尺寸
（3） 边缘填充
（4） 卷积核个数
 
 

• 步长与卷积核大小对结果的影响
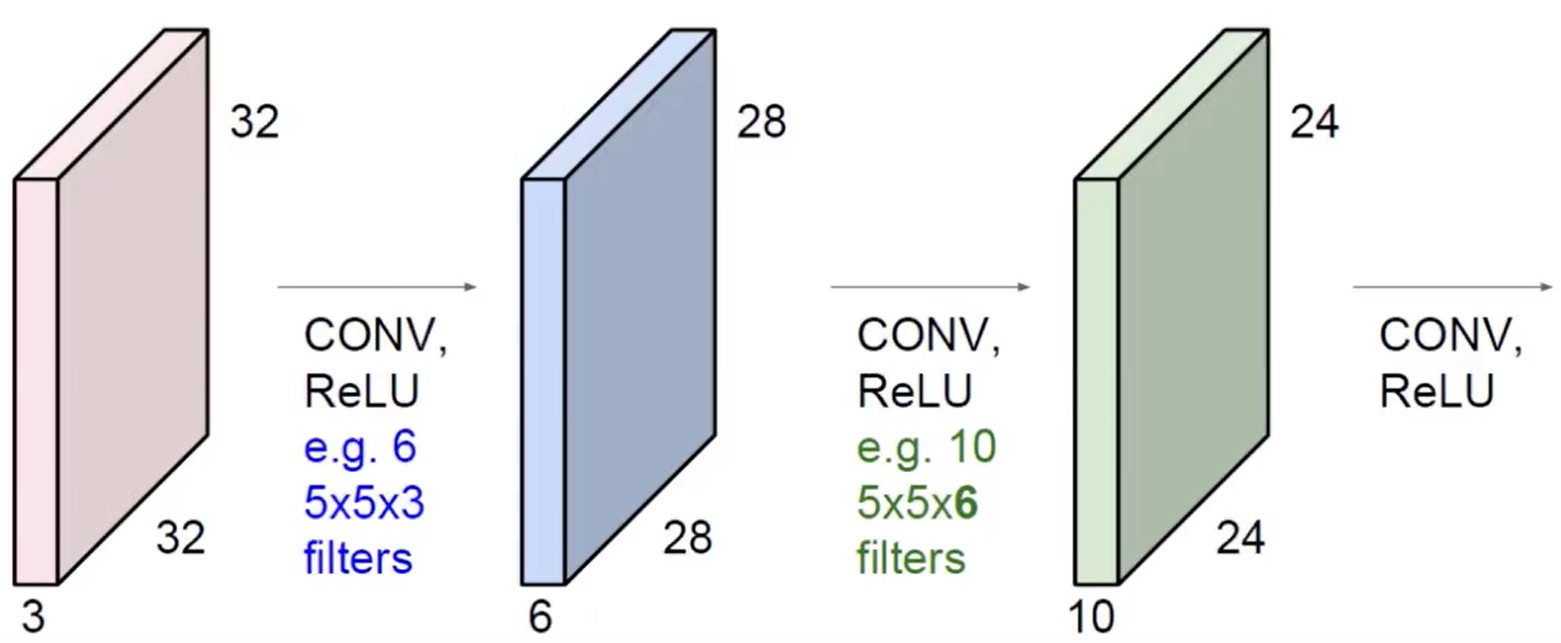
  在卷积神经网络中往往需要进行多次卷积，如下图所示：
  
  堆叠的卷积层可以用下图中的例子来理解其维度的变化：
  

步长也会影响输出的结果，如下图所示：

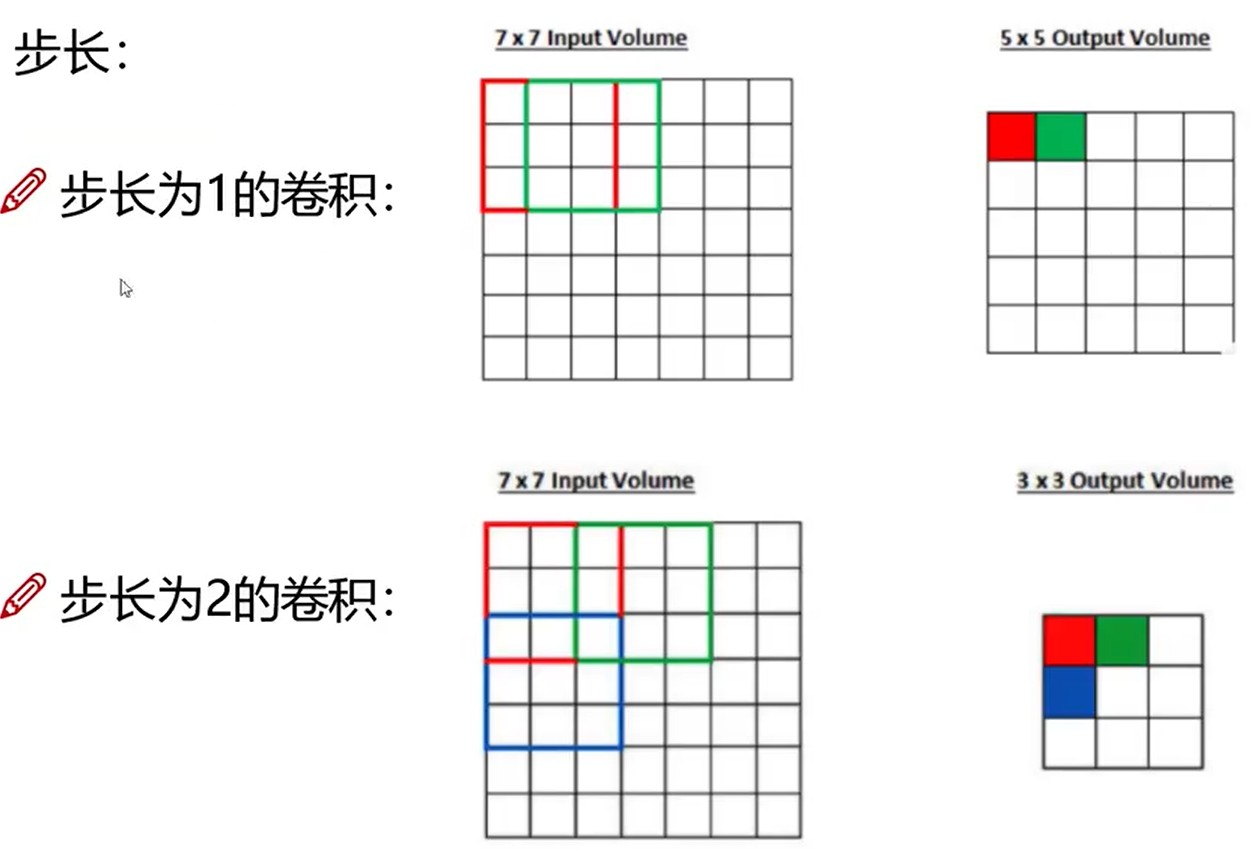
• 边缘填充方法
  边缘填充一定程度上弥补了边界信息缺失的问题

• 特征图尺寸计算与参数共享
  卷积结果尺寸计算公式：$ D_2=\left\lfloor\frac{D_1-F+2P}{S}+1\right\rfloor $

其中D1表示输入的尺寸，D2表示输出的尺寸，F表示卷积核的大小，S表示滑动窗口的步长，P表示边界填充
如果步长为1，填充大小只要满足$ P=\frac{F-1}{2} $，输入输出的大小就是一致的

 
 
图像的底层特征是跟具体位置无关的，故对于主要用于提取底层特征的前几层网络，每一个位置选用相同的卷积核，在这种思想下，可以通过下面的例子体会一下卷积神经网络中有多少参数：

• 数据是32*32*3的图像，用10个5*5*3的filter进行卷积操作，所需的权重参数为：5*5*3*10=750，同时还有b参数，每个卷积核都有一个对应的偏置参数，故最终需要750+10=760个参数

转置卷积

转置卷积(Transposed Convolution)也称为反卷积，可以理解为卷积的逆过程

转置卷积结果尺寸计算公式：$ D_2=(D_1-1)\times S-2\times P+F $

其中D1表示输入的尺寸，D2表示输出的尺寸，F表示卷积核的大小，S表示滑动窗口的步长，P表示边界填充

在Pytorch中，转置卷积层的参数还含有output_padding，用于解决输出大小不唯一(歧义)的问题，因此转置卷积的结果尺寸计算公式变为：$ D_2=(D_1-1)\times S-2\times P+F+OutputPadding $

空洞卷积

如何在Pytorch中实现这些卷积

为了和之前的原理对应，这里只介绍Pytorch中这几种卷积的二维形式，如下：

• torch.nn.Conv2d
• torch.nn.ConvTranspose2d