【研究生学习】移动通信系统学习——移动通信电波传播与传播预测模型与matlab中的AWGN以及瑞利信道

章节知识

概述

对于无线信道的电波传播，可以如下图简单建模：

其中 $ r=h*s+n $，n是高斯白噪声
而h有所不同，比如当 $ h=\delta(t) $ 时，$ r=s+n $
而在无线通信中h就比较复杂，比如可以建模成 $ h=\sum_{i=0}^N exp(-j\varphi_i) $

如果一个噪声，其幅度分布服从高斯分布，功率谱密度是均匀分布的，则称其为高斯白噪声。而之所以被称为“白”，是因为白光是由各种频率(颜色)的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是白色的，此信号也被称为白噪声。
而信道h的不同也会导致传输性能发生变化，如下图所示：

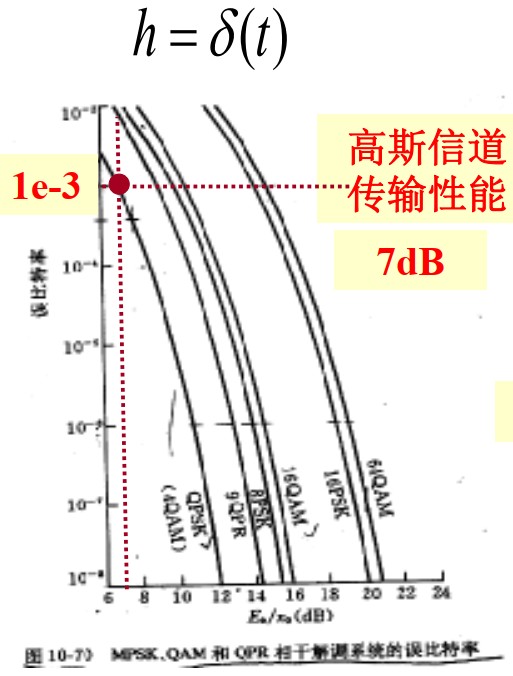
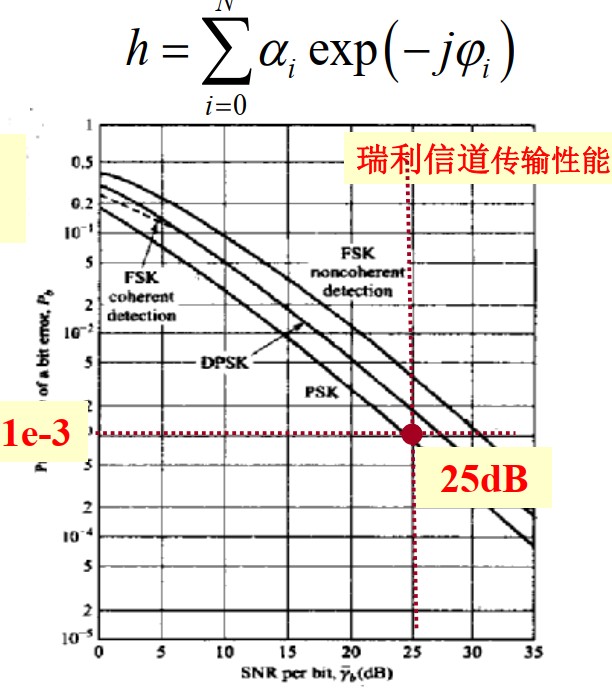
信道可以按照是否存在视距分类，分为视距信道 和 非视距信道：

• 视距信道：直射传播(LOS：Light-Of-Sight)，即直射波，是最强的，比如卫星传播信道
• 非视距信道：非直射传播(Non-LOS)：绕射(次强)、散射(最弱)、反射(次强)

自由空间的电波传播

研究自由空间的电波传播，就要对天线有一定的了解，对于各向同性天线，是没有体积、不存在损耗的点源辐射器。其方向图为球体，在各个方向具有相同的辐射强度，如下图所示：

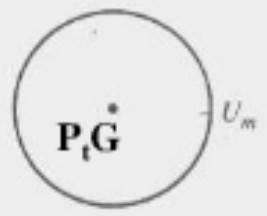
而对于方向性天线，其在某方向的某位置达到辐射场强Um的发射功率为Pt，而均匀辐射的点源天线所需的功率P0，则可定义天线增益$ G=\frac{P_0}{P_t} $，如下图所示：

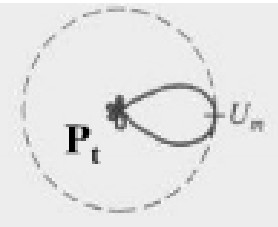
可推导自由空间的电波传播公式如下：

• 发射天线为各向均匀辐射时，以发射源为中心，d为半径的球面上单位面积的功率为：

\[S_{ave}=\frac{P_T}{4\pi d^2}(W/m^2) \]

• 如果天线具有方向性(发射天线增益为GT)，在主波束方向通过单位面积的功率为：

\[S_D=G_T*S_{ave}=\frac{P_TG_T}{4\pi d^2}(W/m^2) \]

• 接收天线有效面积：

\[A_R=\frac{\lambda^2}{4\pi}G_R \]

• 接收天线所截获的功率为：

\[P_R=P_TG_TG_R(\frac{\lambda}{4\pi d})^2(W) \]

• 定义传播损耗，也称为路径损耗：

\[L=\frac{P_T}{P_R}=(\frac{4\pi d}{\lambda})^2\frac{1}{G_TG_R} \]

当GT=GR=1时，自由空间的传播损耗(其中f的单位改为MHz，d的单位改为km)：

\[L_{dB}=10lg(L)=10lg((\frac{4\pi d}{\lambda})^2)=10lg((\frac{4\pi}{c})^2d^2f^2)=32.45+20lgf+20lgd \]

当GT和GR非1时，自由空间的传播损耗为：

\[L_{dB}=32.45+20lgf+20lgd-10lgG_T-10lgG_R \]

由于在移动无线系统中通常接收电平的动态范围很大，因此计算功率时常用dBm和dBW作为单位，，其换算关系如下：

\[P_{dBm}(dBm)=10log(P(mW)) \]

\[P_{dBW}(dBW)=10log(P(W)) \]

比如，1W=30dBm

对于非理想的自由空间传输损耗，实测表明，在发射功率，天线参数和工作频率给定的条件下，平均路径损耗为：

\[P(d) \propto (\frac{d}{d_0})^n 当d>d0 \]

• d0为靠近发端的参考点距发端的距离，该处的损耗可以由实测获取
• n为路径损耗指数，取决于传播环境
  典型环境的路径损耗指数如下图所示：
  
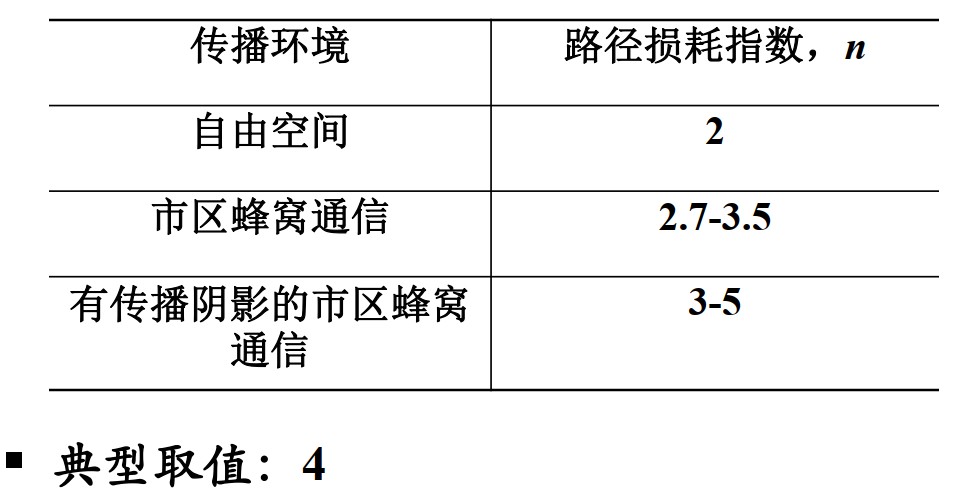
  对数距离路径损耗模型：$ L_{dB}=L(d_0)+10nlg(\frac{d}{d_0}) $

3种基本电波传播机制

• 反射：阻挡体比传输波长大得多的物体，也是产生多径衰落的主要因素
• 绕射：阻挡体具有尖锐边缘，频率越低，绕射能力越强
• 散射：产生于粗糙表面、小物体或其他不规则物体

无线电波频段划分如下图所示：

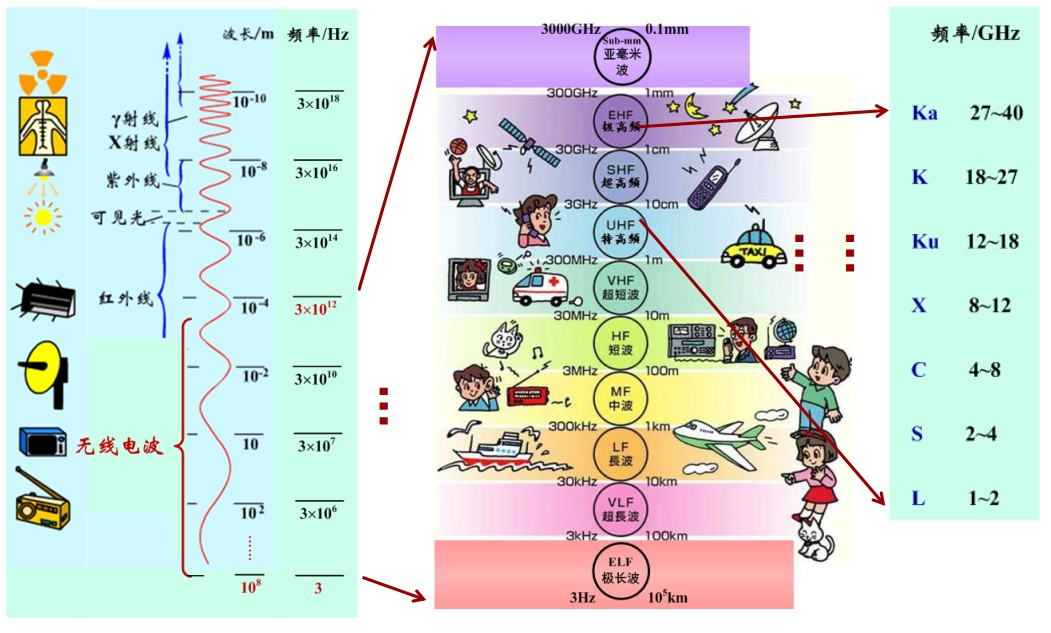
阴影衰落的基本特性

阴影衰落就是由移动无线通信信道传播环境中的地形起伏、建筑物及其他障碍物对电波路径的阻挡而形成的电磁场半盲区，也称为阴影效应，如下图所示：

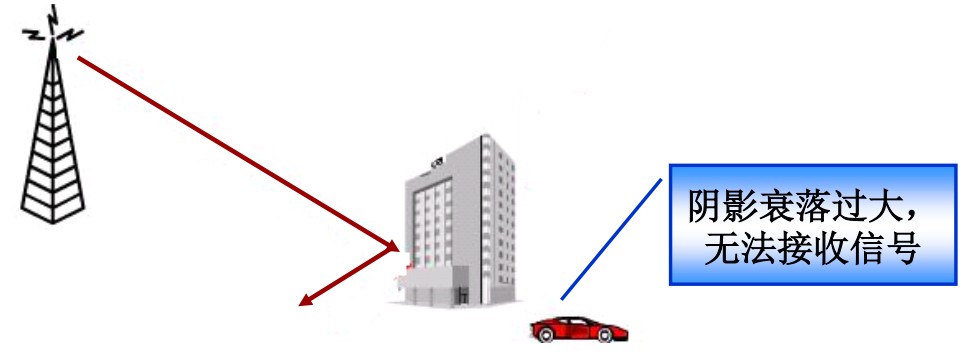
传播损耗也受阴影衰落的影响，可表示如下：

\[l(r,\zeta)=r^m*10^{\frac{\zeta}{10}} \]

• r：传播距离，m为路径损耗指数
• ζ：阴影产生的对数损耗，服从均值为0，方差为σ的正态分布
  对数形式表示为：

\[10lgl(r,\zeta)=10mlgr+ζ \]

移动无线信道及特征参数

无线信道的衰落分为大尺度衰落和小尺度衰落：

• 大尺度衰落：用于描述发射机与接收机之间的长距离(几百或几千米)或长时间上信号强度的变化
• 小尺度衰落：用于描述发射机与接收机之间的短距离(几个波长)或短时间(秒级)内信号强度的快速变化
  大尺度衰落和小尺度衰落的示意如下图所示：
  
  其各自造成的损耗有不一样的特征，如下图所示：
  

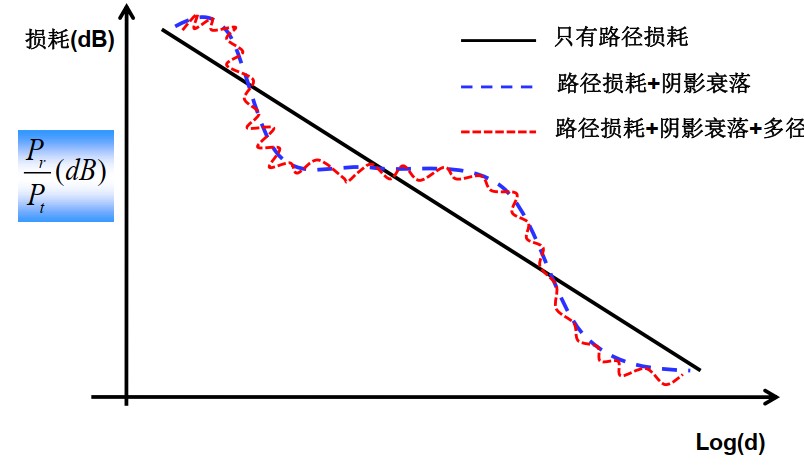
可以看出无线通信信道的响应$ h(t)=m(t)*r_0(t) $ ，式中：

• $ m(t) $：大尺度衰落/长期慢衰落，主要由路径损耗和阴影衰落造成。从无线系统工程的角度看，传播的衰落主要影响到无线区的覆盖
• $ r_0(t) $：小尺度衰落/短期快衰落，主要由移动台的运动和环境变化产生，主要特征是多径。多径产生时间扩散，引起信号符号间干扰；运动产生多普勒效应，引起信号随机调频
  两种衰落是共同作用的

多径衰落的基本特性

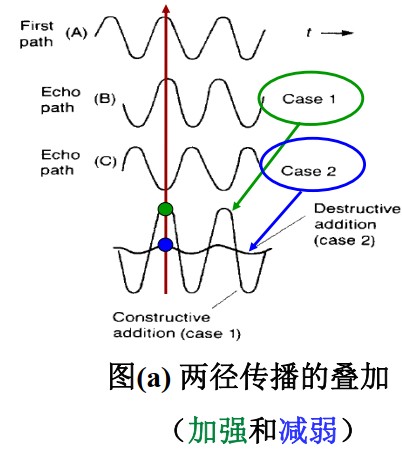
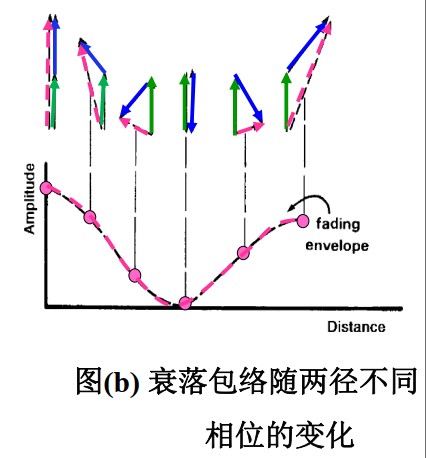
在移动通信环境中，发射的电波经历了不同路径，导致传播时间和相位均不相同，故接收信号的幅度在较短时间内急剧变化，产生了衰落
多径衰落可由下面的两张图直观看出，第一张图是两径传播的叠加(加强和减弱)，第二张图是衰落包络随两径不同相位的变化：

多普勒频移

多普勒效应：移动台在移动中通信，接收信号频率会发生变化的现象，其推导如下：

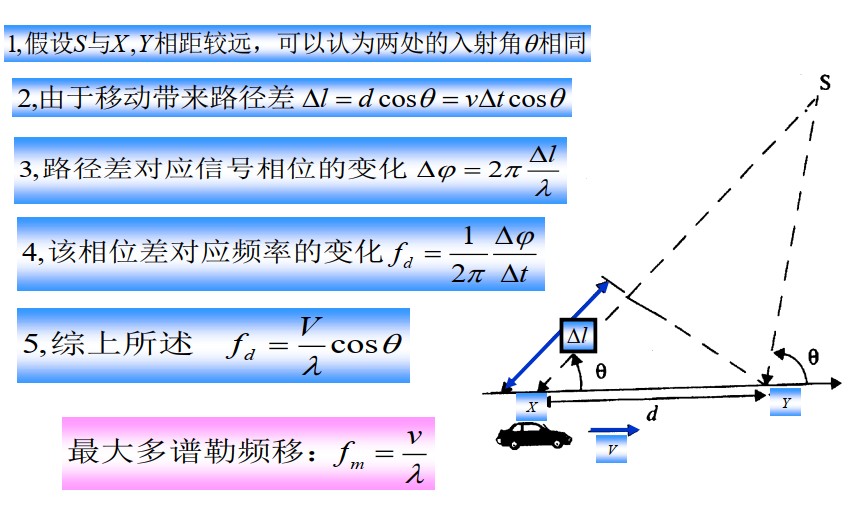
其中$ f_c $ 为信号频率，c为光速，信号波长为 $ \lambda=\frac{c}{f_c} $
可见，多普勒效应具有如下特点：

• 移动台朝着入射波方向运动，多普勒频移为正
• 移动台背向入射波方向运动，多普勒频移为负
• 由于接收信号是发送信号经过不同方向传播后的叠加，形成多普勒扩展，$ f_d\in[-f_m,f_m] $

多径信道的信道模型

将信道看成作用于信号上的滤波器，可以通过分析滤波器的冲激响应和传递函数得到多径信道的特性
假设传输信号为：

\[x(t)=Re\left\{s(t)exp(j2\pi f_ct)\right\} \]

当信号通过无线信道时，会受到多径信道的影响而产生多径效应，故假设第i径的路径长度为xi，衰落系数为ai，则接受信号可表示为：

\[y(t)=\sum_ia_ix(t-\frac{x_i}{c})=\sum_ia_iRe\left\{s(t-\frac{x_i}{c})exp[j2\pi f_c(t-\frac{x_i}{c})]\right\}=Re\left\{\sum_ia_is(t-\frac{x_i}{c})exp[j2\pi (f_ct-\frac{x_i}{\lambda})]\right\} \]

可推导出接受信号的包络：

\[y(t)=Re\left\{r(t)exp(j2\pi f_ct)\right\} \]

r(t)是接收信号的复包络模型：

\[r(t)=\sum_ia_iexp(-j2\pi \frac{x_i}{\lambda})s(t-\frac{x_i}{c})=\sum_ia_iexp(-j2\pi f_c\tau_i)s(t-\tau_i) \]

再考虑多普勒频移，假设路径i的到达方向和移动台运动方向之间的夹角为θi，则路径的变化量为：

\[\Delta x_i=-vtcos\theta_i \]

此时信号输出的复包络为：

\[r(t)=\sum_ia_iexp(-j2\pi \frac{x_i+\Delta x_i}{\lambda})s(t-\frac{x_i+\Delta x_i}{c})=\sum_ia_iexp(-j2\pi \frac{x_i}{\lambda})exp(j2\pi \frac{v}{\lambda}tcos\theta_i)s(t-\frac{x_i}{c}+\frac{vtcos\theta_i}{c}) \]

对于上式可以进行化简，由于$ \frac{vtcos\theta_i}{c}的数量级比\frac{x_i}{c} $ 小得多，故可以忽略其在时延变化量的影响，但不可以忽略其在相位中的影响，故上式变为：

\[r(t)=\sum_ia_iexp(j2\pi [\frac{v}{\lambda}tcos\theta_i-\frac{x_i}{\lambda}])s(t-\frac{x_i}{c})=\sum_ia_is(t-\tau_i)exp(-j[2\pi f_c\tau_i-2\pi f_mtcos\theta_i]) \]

上式就体现了多径和多普勒效应对传输信号s(t)施加的影响，进一步可以得到信道的冲激响应函数：

\[h(t,\tau)=\sum_ia_i(t)e^{-j\phi_i(t)}\delta(\tau-\tau_i(t)) \]

研究表明相位$ \phi_i $服从[0,2π]的均匀分布，多径信号的个数，每个多径信号的幅度以及时延需要进行测试，找出其统计规律。

多径信道的统计分析

由上一节中可得：

\[r(t)=\sum_ia_is(t-\tau_i)exp(-j\phi_i) \]

定义：

\[T_c(t)=Re(r(t)) \]

\[T_s(t)=Im(r(t)) \]

由中心极限定理，大量相互独立同分布的变量和服从高斯分布，故当N->∞时，$ T_c(t) $ 和$ T_s(t) $ 为高斯随机过程，其概率密度函数如下：

\[\]

多径信道主要参数与多径衰落信道分类

多径信道主要参数如下：

• 时间色散参数和相关带宽
• 频率色散系数和相干时间
• 角度色散参数和相关距离

时间色散参数和相关带宽

时域上分析：存在时延扩展，即最大传输时延和最小传输时延的差值，也可以是最后一个可分辨的时延信号与最早的时延信号到达时间的差值
时延扩展可以如下图所示：

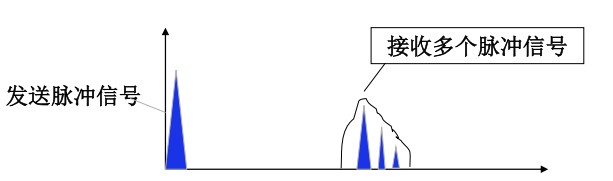
而从数学的角度上，可以通过功率的延迟分布来定义两个数学量：平均时延和均方值时延扩展，功率延迟分布的示意如下图所示：

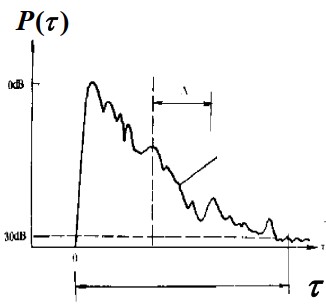
• 平均时延

\[\overline{\tau}=\frac{\sum_kP(\tau_k)\tau_k}{\sum_kP(\tau_k)} \]

• 均方值时延扩展

\[\sigma_{\tau}^2=E(\tau^2)-(\overline{\tau})^2=\frac{\sum_kP(\tau_k)\tau_k^2}{\sum_kP(\tau_k)}-(\frac{\sum_kP(\tau_k)\tau_k}{\sum_kP(\tau_k)})^2 \]

以下有道例题，可以理解以下这些参数如何计算：

在时域上的分析中，衰落可以分为频率选择性衰落以及平坦衰落，主要要比较发送信号的码元周期\(T_s\) 与信道时延扩展$ \sigma_{\tau} $

• 平坦衰落信道
• 频率选择性衰落

衰落特性的度量

衰落特性即衰落包络与时间的关系

• 衰落率：信号包络在单位时间内以正斜率通过中值电平的次数
• 衰落深度：信号的有效值与该次衰落的信号最小值的差值
• 电平通过率(LCR，Level Cross Rate)：信号包络在单位时间内以正斜率通过某一规定电平值R的平均次数，描述衰落次数的统计规律
• 平均衰落持续时间(ADF，Average Duration of Fades)：信号包络低于某个给定电平值的时间与该电平对应的电平通过率之比
  衰落特性具有工程意义，当接收信号电平低于接收机门限电平时，就可能导致语音中断或者误比特率突然增大。故衰落特性的研究可以帮助判定语音受影响的程度，以及在数字通信中是否会发生突发性错误和突发错误的长度，对于设计纠错控制编码和分集方案十分有用。

simulink仿真

为了进一步理解本章的知识，在simulink中搭建相关的链路来加以应用，实验的链路为QPSK发送链路，经过瑞利衰落信道，使用的matlab版本为R2021a，实验参数如下：

• 信源比特速率为500kbps
• 多径相对时延为[0 4e-06 8e-06 1.2e-05]
• 相对平均功率为[0 -3 -6 -9]dB
• 最大多普勒频移为200Hz
  实验主要观察瑞利信道的一些信道特征图，比如Impulse Response、Frequency Response和Doppler Spectrum，同时还要观察信号经过瑞利衰落前后的星座图变化
  在simulink中搭建的链路如下图所示：
  
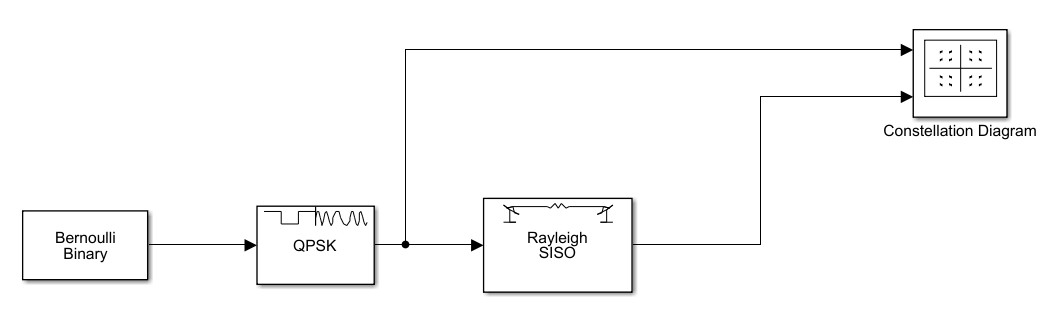
  其中信源采用伯努利二进制发生器模块，模块的Sample time参数根据实验要求设置为1/500e3即可，而Samples per frame参数设置每一帧的输出个数；调制模块直接使用QPSK基带调制模块，信源采用的是伯努利二进制输出，因此Input type参数为bit。
  信道采用的是SISO Fading Channel模块，这个模块是实验主要用到的模块，其参数有两个部分，一个是Main，另一个是Visualization：
• Visualization：可以自行设置仿真时显示哪些信道的参数，包括Impulse response、Frequency Response、Doppler Spectrum和Impulse and Frequency Response，当然也可以选择Off关掉，后面就用这种可视化的方式直观观察一下信道的特征
• Main：这个选项主要设置信道的一些参数，有以下参数：
  • Discrete path delay(s)
  • Average path gains(dB)
  • Fading distribution
  • Maximum Doppler shift(Hz)
  • Doppler spectrum
  • Output channel path gains
  • Output channel filter delay

在仿真一些通信链路的性能时，一般用到的是matlab，这篇博客介绍一下matlab的通信模块中的AWGN信道部分

matlab中的AWGN信道

实例说明

现在就用下面的几个实际的通信系统的仿真例子来看一下如何运用上面的公式，通信系统直接使较用matlab中的simulink搭建，这样子比直观，我使用的matlab版本是R2021a

BPSK、QPSK、16QAM通信链路

在simulink中搭建BPSK、QPSK、16QAM的通信链路如下图所示，经过AWGN信道以及解调后统计误比特率，并与bertool中的理论误比特率进行分析比较

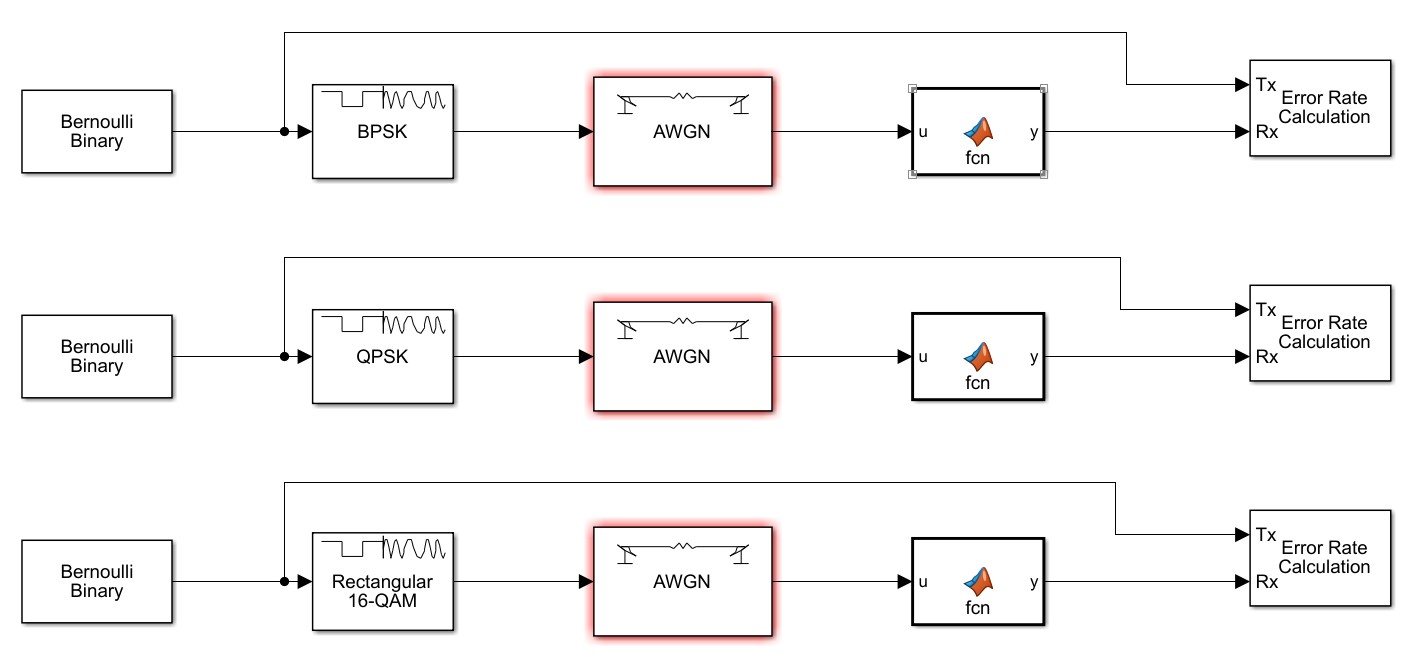
链路的具体参数如下：

• 信源比特速率：1Mbps(即伯努利二进制发生器模块的Sample time参数设置为1e-6)
• AWGN模块

OFDM