回归分析

回归分析

相关分析是研究两个或两个以上的变量之间相关程度及大小的一种统计方法

回归分析是寻找存在相关关系的变量间的数学表达式，并进行统计推断的一种统计方法

在对回归分析进行分类时，主要有两种分类方式：

• 根据变量的数目，可以分类一元 回归、多元回归

• 根据自变量与因变量的表现形式，分为线性与非线性

所以，回归分析包括四个方向：一元线性回归分析、多元线性回归分析、一元非线性回归分析、多元非线性回归分析。

回归分析的一般步骤：

一元线性回归分析

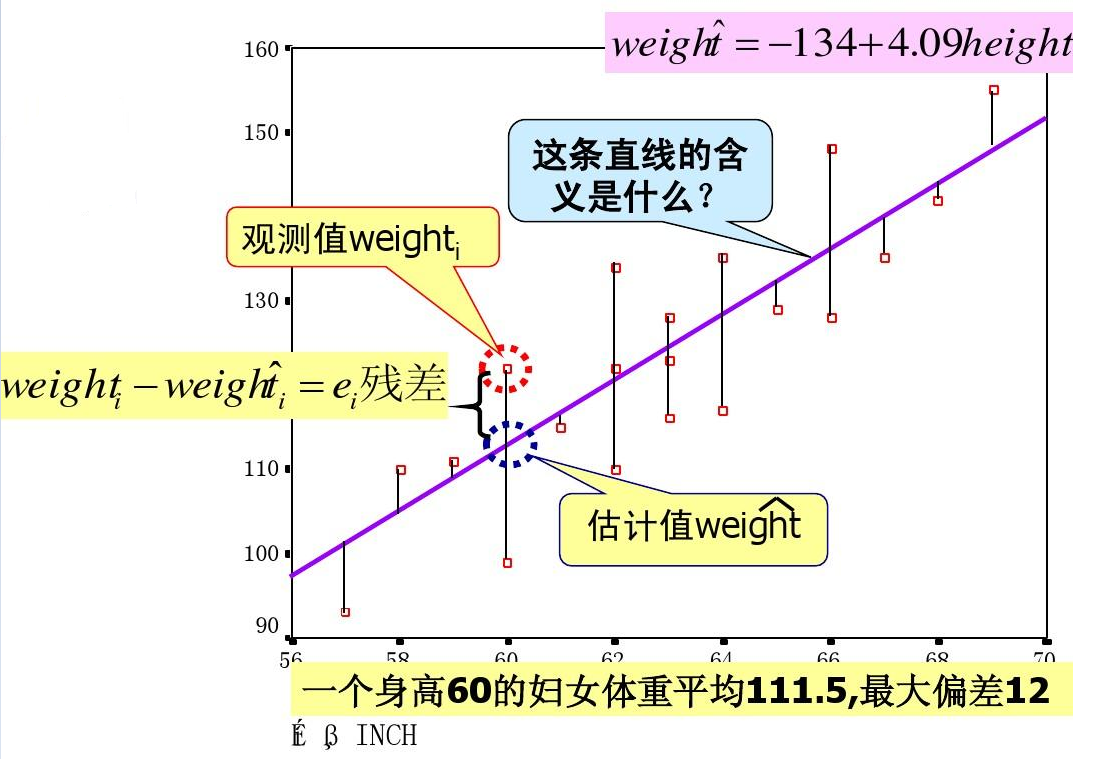
• 因变量(dependent variable)：被预测或被解释的变量，用y表示

• 自变量(independent variable)：预测或解释因变量的一个或多个变量，用x表示

• 对于具有线性关系的两个变量，可以用一个方程来表示它们之间的线性关系

• 描述因变量y如何依赖于自变量x和误差项ε的方程称为回归模型。对于只涉及一个自变量的一元线性回归模型可表示为：

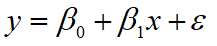
• y叫做因变量或被解释变量
• x叫做自变量或解释变量
• β0 表示截距
• β1 表示斜率
• ε表示误差项，反映除x和y之间的线性关系之外的随机因素对y的影响

一元小例子：

• 人均收入是否会显著影响人均食品消费支出

• 贷款余额是否会影响到不良贷款

• 航班正点率是否对顾客投诉次数有显著影响

回归方程

描述因变量y的期望值如何依赖于自变量x的方程称为回归方程。根据对一元线性回归模型的假设，可以得到它的回归方程为：

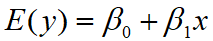
• 如果回归方程中的参数已知，对于一个给定的x值，利用回归方程就能计算出y的期望值

• 用样本统计量代替回归方程中的未知参数 ，就得到估计的回归方程，简称回归直线

参数的最小二乘法估计

对于回归直线，关键在于求解参数，常用高斯提出的最小二乘法，它是使因变量的观察值y与估计值之间的离差平方和达到最小来求解

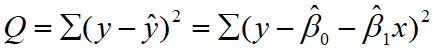
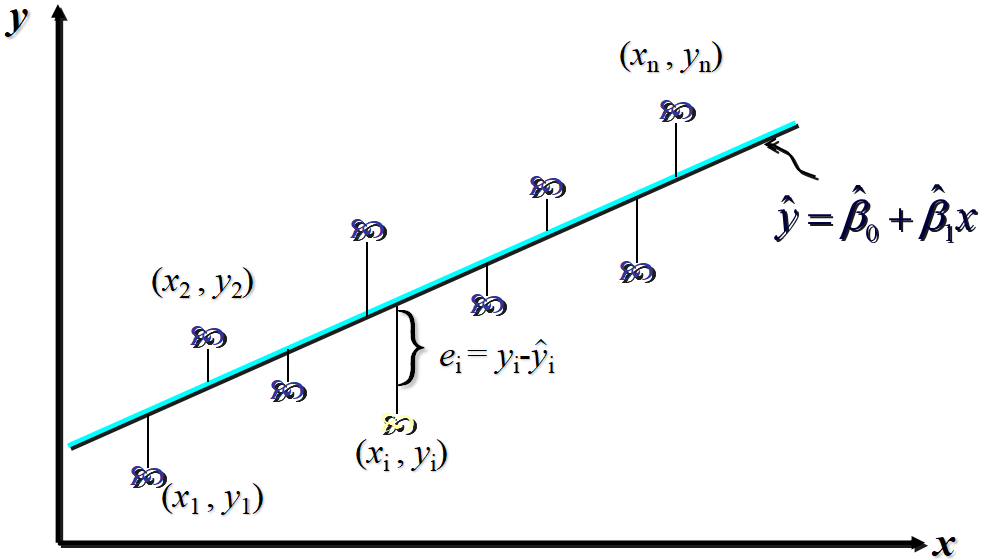
展开可得：

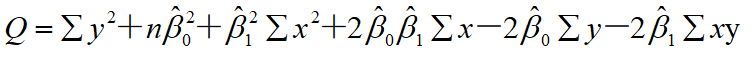
求偏导可得：

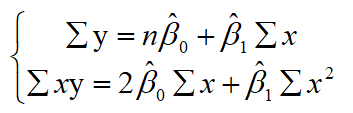
求解：

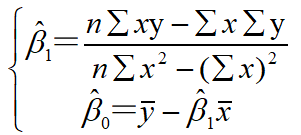
实例：70年代世界制造业总产量与世界制成品总出口量的变化关系如表

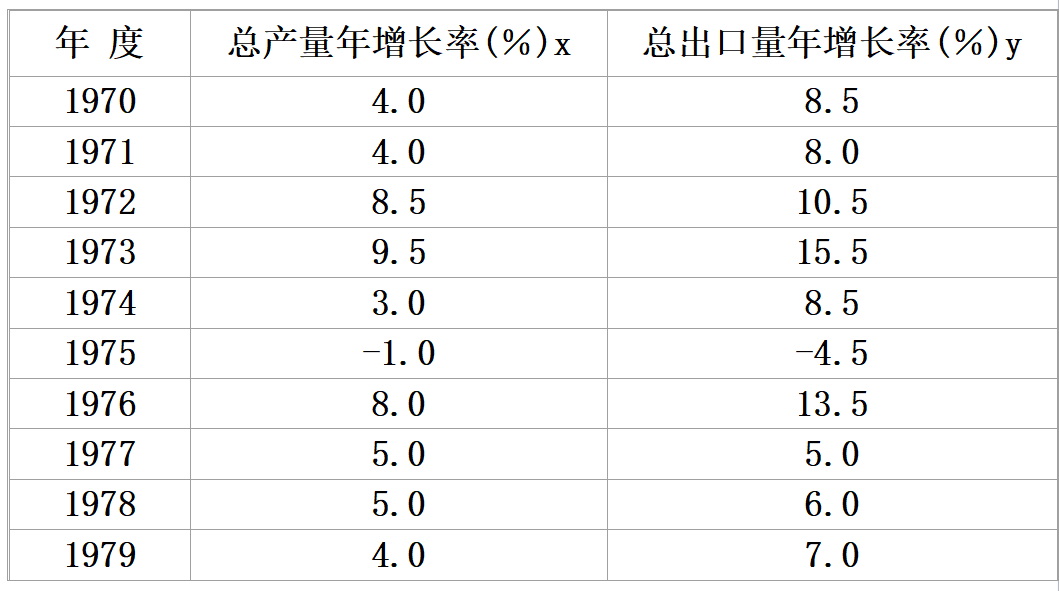
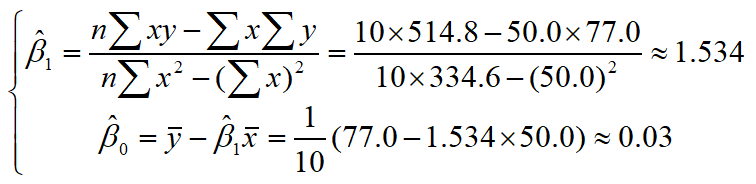
利用回归直线进行估计和预测：

• 点估计：利用估计的回归方程，对于x的某一个特定的值 ，求出y的一个估计值 就是点估计

• 区间估计：利用估计的回归方程，对于x的一个特定值 ，求出y的一个估计值的区间就是区间估计

估计标准误差的计算

为了度量回归方程的可靠性，通常计算估计标准误差。它度量观察值回绕着回归直线的变化程度或分散程度。

估计平均误差：

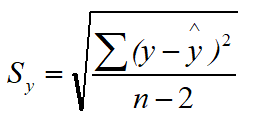
• 公式中根号内的分母是n-2,而不是n，因而自由度为n-2。

• 估计标准误差越大，则数据点围绕回归直线的分散程度就越大，回归方程的代表性越小。

• 估计标准误差越小，则数据点围绕回归直线的分散程度越小，回归方程的代表愈大，其可靠性越高。

置信区间估计：

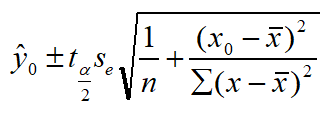
在1－α置信水平下预测区间为：

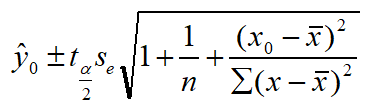
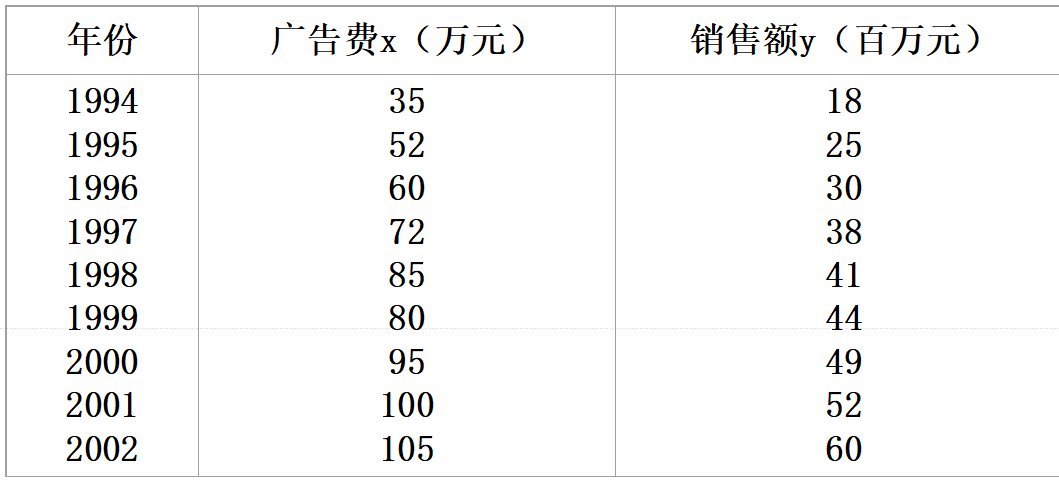
某企业从有关资料中发现广告投入和产品销售有较密切的关系。近年该企业广告费和销售额资料见表10-3，若2003年广告费为120万元，请用一元线性回归求2003年产品销售额的置信区间与预测区间（α＝0.05）

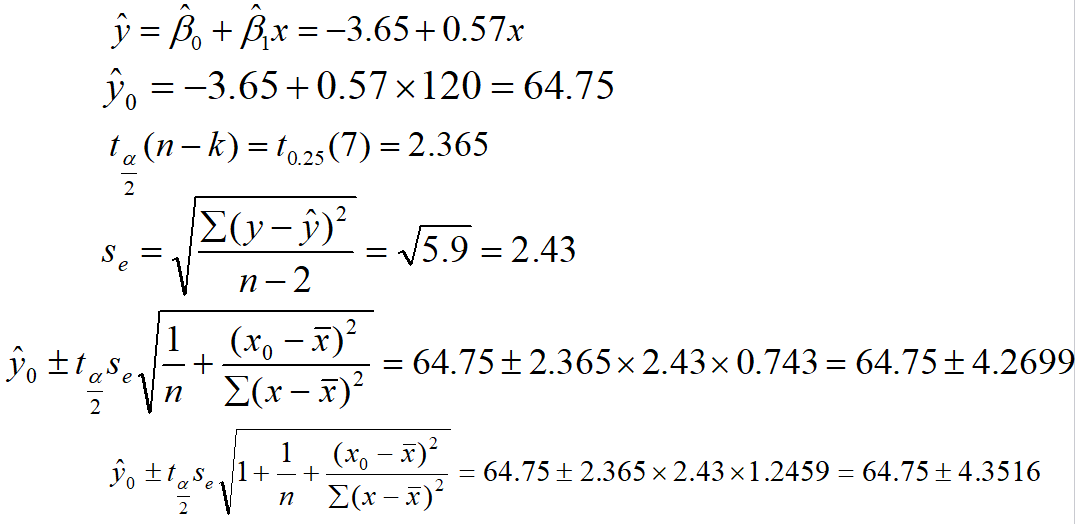
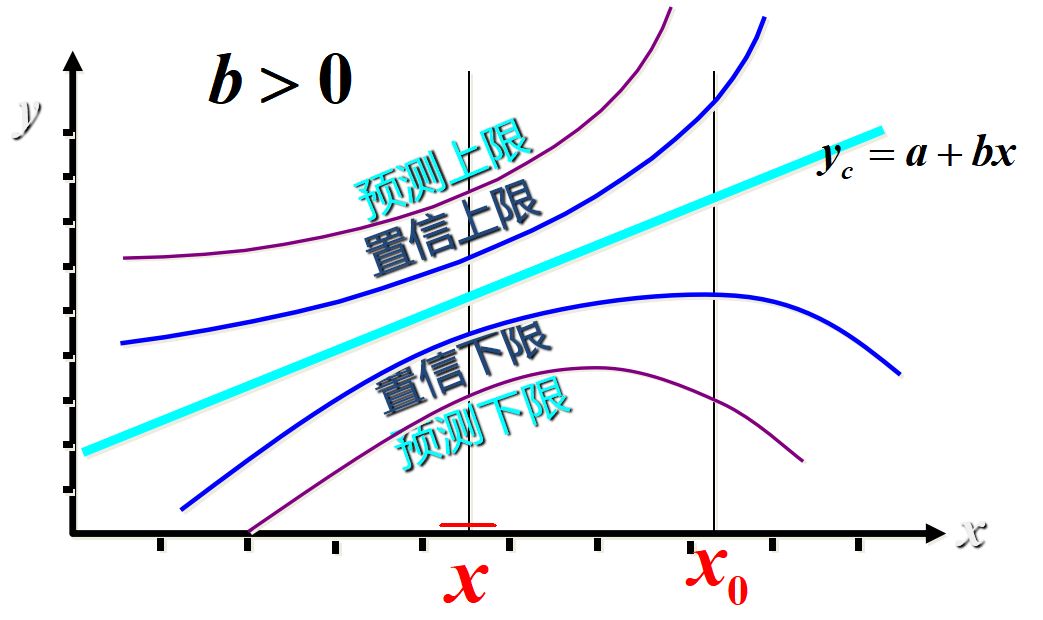
影响区间宽度的因素：

• 置信水平 (1 - α)，区间宽度随置信水平的增大而增大

• 数据的离散程度Se，区间宽度随离程度的增大而增大

• 样本容量，区间宽度随样本容量的增大而减小

• X0与X均值之间的差异，随着差异程度的增大而增大

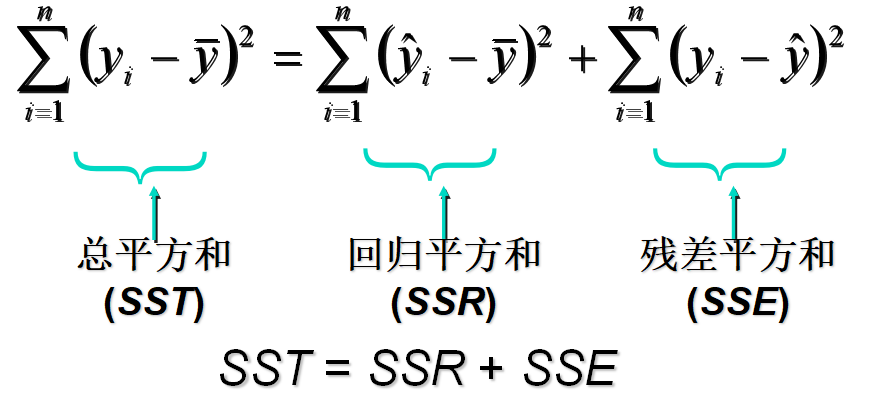
回归直线的拟合优度

回归直线与各观测点的接近程度称为回归直线对数据的拟合优度

• 总平方和（SST）：

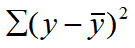
• 回归平方和（SSR）：

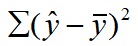
• 残差平方和（SSE）：

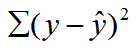
总平方和可以分解为回归平方和、残差平方和两部分：SST＝SSR+SSE

• 总平方和(SST)，反映因变量的 n 个观察值与其均值的总离差

• 回归平方和SSR反映了y的总变差中，由于x与y之间的线性关系引起的y的变化部分

• 残差平方和SSE反映了除了x对y的线性影响之外的其他因素对y变差的作用，是不能由回归直线来解释的y的变差部分

判定系数

回归平方和占总平方和的比例，用R^2表示,其值在0到1之间。

• R^2 == 0：说明y的变化与x无关，x完全无助于解释y的变差

• R^2 == 1：说明残差平方和为0，拟合是完全的，y的变化只与x有关

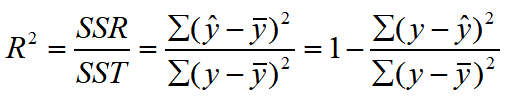
显著性检验

显著性检验的主要目的是根据所建立的估计方程用自变量x来估计或预测因变量y的取值。当建立了估计方程后，还不能马上进行估计或预测，因为该估计方程是根据样本数据得到的，它是否真实的反映了变量x和y之间的关系，则需要通过检验后才能证实。

根据样本数据拟合回归方程时，实际上就已经假定变量x与y之间存在着线性关系，并假定误差项是一个服从正态分布的随机变量，且具有相同的方差。但这些假设是否成立需要检验

显著性检验包括两方面：

• 线性关系检验

• 回归系数检验

线性关系检验

线性关系检验是检验自变量x和因变量y之间的线性关系是否显著，或者说，它们之间能否用一个线性模型来表示。

将均方回归 (MSR)同均方残差 (MSE)加以比较，应用F检验来分析二者之间的差别是否显著。

• 均方回归：回归平方和SSR除以相应的自由度(自变量的个数K)

• 均方残差：残差平方和SSE除以相应的自由度(n-k-1)

H0：β1=0 所有回归系数与零无显著差异，y与全体x的线性关系不显著

计算检验统计量F：

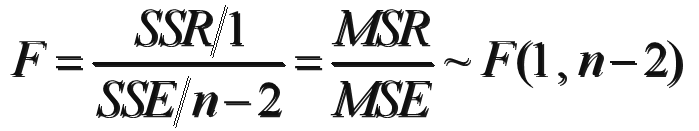
回归系数的显著性检验

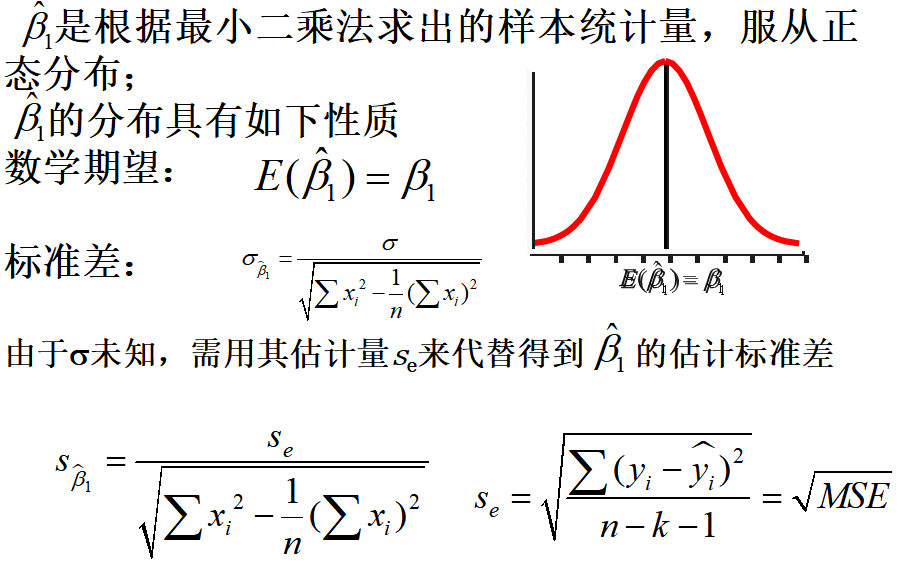
回归系数显著性检验的目的是通过检验回归系数β的值与0是否有显著性差异，来判断Y与X之间是否有显著的线性关系.若β=0,则总体回归方程中不含X项(即Y不随X变动而变动),因此,变量Y与X之间并不存在线性关系;若β≠0,说明变量Y与X之间存在显著的线性关系。

计算检验的统计量：

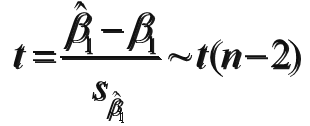
线性关系检验与回归系数检验的区别：

线性关系的检验是检验自变量与因变量是否可以用线性来表达，而回归系数的检验是对样本数据计算的回归系数检验总体中回归系数是否为0

• 在一元线性回归中，自变量只有一个，线性关系检验与回归系数检验是等价的

• 多元回归分析中，这两种检验的意义是不同的。线性关系检验只能用来检验总体回归关系的显著性，而回归系数检验可以对各个回归系数分别进行检验

多元线性回归分析

经常会遇到某一现象的发展和变化取决于几个影响因素的情况，也就是一个因变量和几个自变量有依存关系的情况，这时需用多元线性回归分析。

• 多元线性回归分析预测法，是指通过对两上或两个以上的自变量与一个因变量的相关分析，建立预测模型进行预测和控制的方法

• 多元线性回归预测模型一般式为：

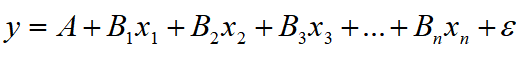
调整的多重判定系数：

用样本容量n和自变量的个数k去修正R^2得到:

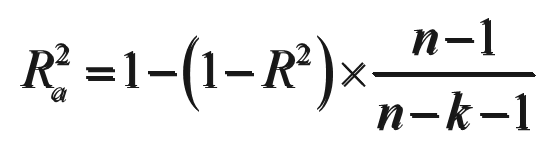
• 避免增加自变量而高估R^2

曲线回归分析：

直线关系是两变量间最简单的一种关系，曲线回归分析的基本任务是通过两个相关变量x与y的实际观测数据建立曲线回归方程，以揭示x与y间的曲线联系的形式。

曲线回归分析最困难和首要的工作是确定自变量与因变量间的曲线关系的类型，曲线回归分析的基本过程：

• 先将x或y进行变量转换
• 对新变量进行直线回归分析、建立直线回归方程并进行显著性检验和区间估计
• 将新变量还原为原变量，由新变量的直线回归方程和置信区间得出原变量的曲线回归方程和置信区间

由于曲线回归模型种类繁多，所以没有通用的回归方程可直接使用。但是对于某些特殊的回归模型，可以通过变量代换、取对数等方法将其线性化，然后使用标准方程求解参数，再将参数带回原方程就是所求。

实例：某商店各个时期的商品流通费率和商品零售额资料

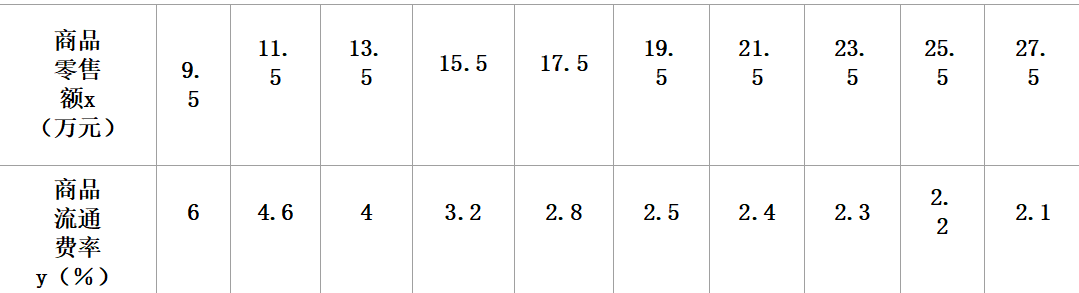
散点图如下：

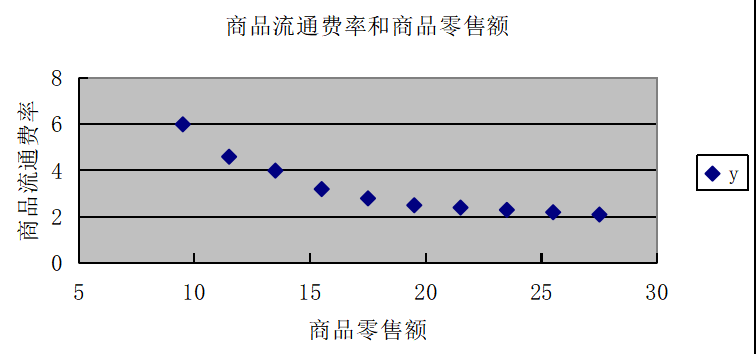
散点图显示出x与y的变动关系为一条递减的双曲线。

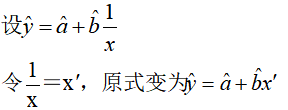
多重共线性

回归模型中两个或两个以上的自变量彼此相关的现象

多重共线性带来的问题有:

• 回归系数估计值的不稳定性增强

• 回归系数假设检验的结果不显著等

多重共线性检验的主要方法:

• 容忍度
• 方差膨胀因子（VIF）

容忍度:

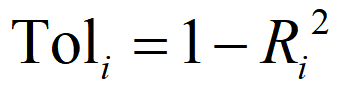
• Ri是解释变量xi与方程中其他解释变量间的复相关系数；
• 容忍度在0~1之间，越接近于0，表示多重共线性越强，越接近于1，表示多重共线性越弱。

方差膨胀因子

方差膨胀因子是容忍度的倒数

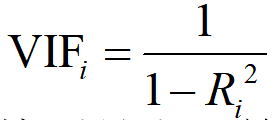
• VIFi越大，特别是大于等于10，说明解释变量xi与方程中其他解释变量之间有严重的多重共线性；
• VIFi越接近1，表明解释变量xi和其他解释变量之间的多重共线性越弱。