方差分析

方差分析

检验多个总体均值是否相等，通过分析察数据的误差判断各总体均值是否相等

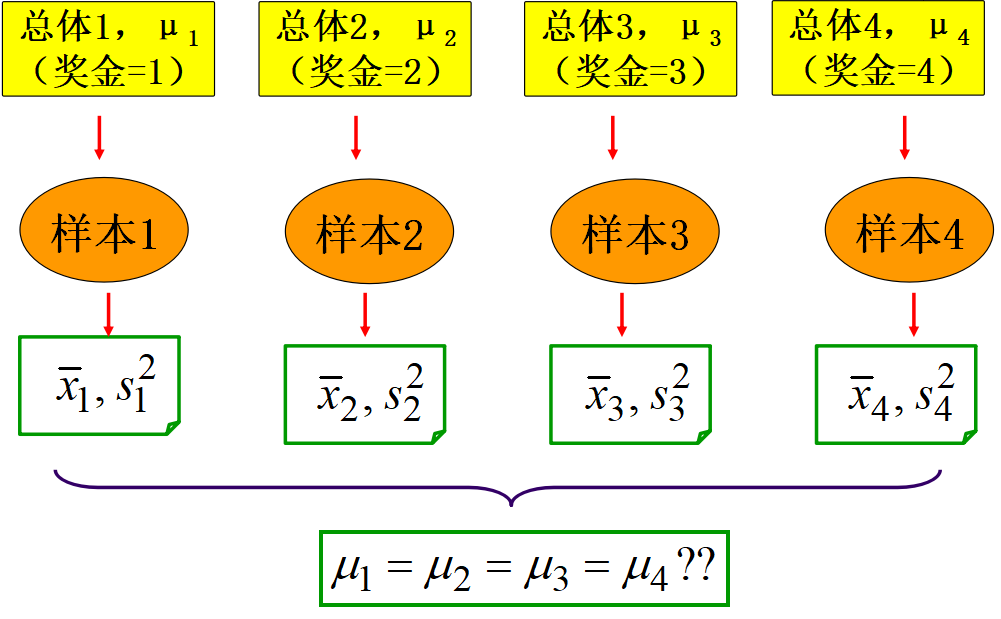
variance1 variance2

实例：

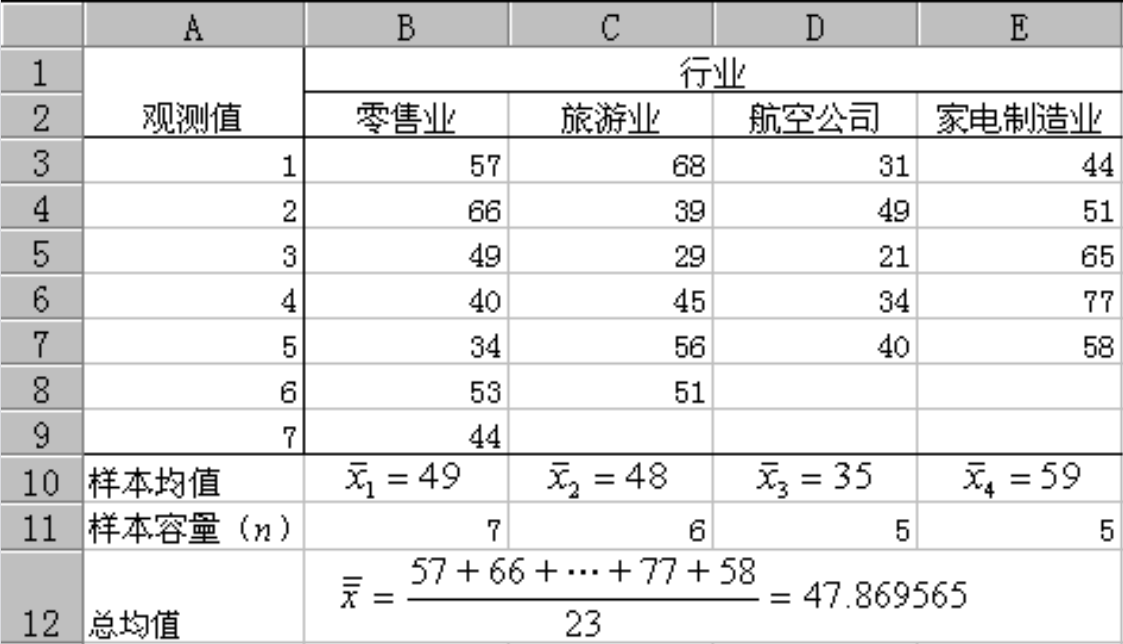
为了对几个行业的服务质量进行评价，消费者协会在四个行业分别抽取了不同的企业作为样本。最近一年中消费者对总共23家企业投诉的次数如下表

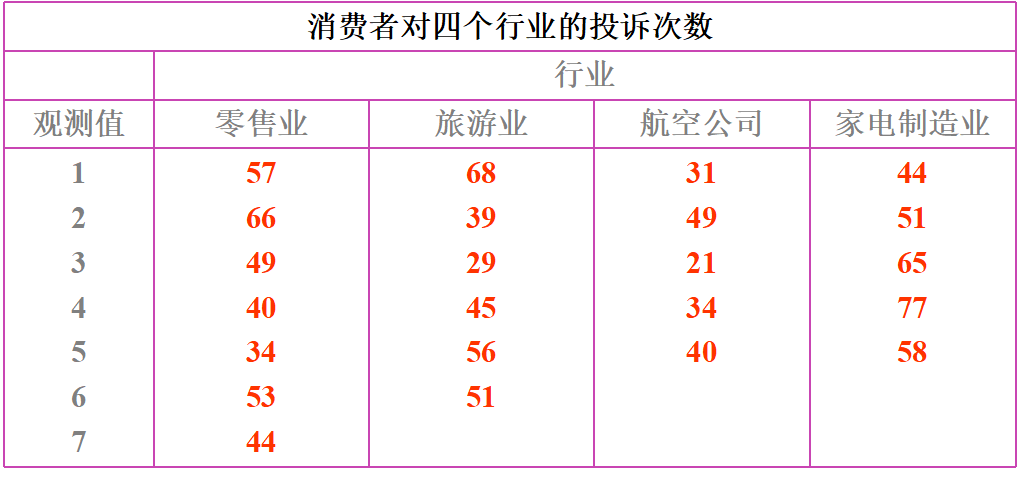
variance3

要做的事：

分析四个行业之间的服务质量是否有显著差异，也就是要判断“行业”对“投诉次数”是否有显著影响

如果它们的均值相等，就意味着“行业”对投诉次数是没有影响的，即它们之间的服务质量没有显著差异；如果均值不全相等，则意味着“行业”对投诉次数是有影响的，它们之间的服务质量有显著差异

相关概念：

  • 因素或因子(factor)：所要检验的对象，要分析行业对投诉次数是否有影响，行业是要检验的因素或因子
  • 水平或处理(treatment)：因素的不同表现，即每个自变量的不同取值称为因素的水平
  • 观察值：在每个因素水平下得到的样本值，每个行业被投诉的次数就是观察值
  • 试验：这里只涉及一个因素，因此称为单因素四水平的试验
  • 总体：因素的每一个水平可以看作是一个总体，比如零售业、旅游业、航空公司、家电制造业可以看作是四个总体
  • 样本数据：被投诉次数可以看作是从这四个总体中抽取的样本数据

散点图观察

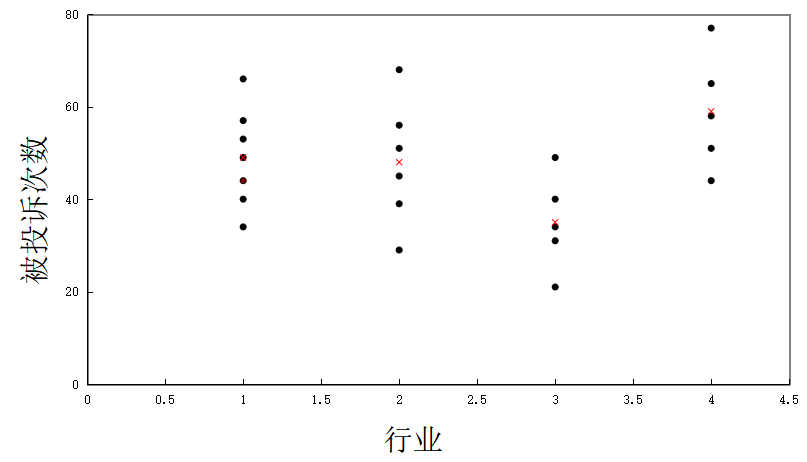
variance5
  • 不同行业被投诉的次数是有明显差异的
  • 即使是在同一个行业，不同企业被投诉的次数也明显不同
  • 家电制造也被投诉的次数较高，航空公司被投诉的次数较低
  • 行业与被投诉次数之间有一定的关系

但是

  • 仅从散点图上观察还不能提供充分的证据证明不同行业被投诉的次数之间有显著差异

  • 这种差异也可能是由于抽样的随机性所造成的

  • 需要有更准确的方法来检验这种差异是否显著，也就是进行方差分析

  • 之所以叫方差分析，因为虽然我们感兴趣的是均值，但在判断均值之间是否有差异时则需要借助于方差

基本思想：

  • 比较两类误差，以检验均值是否相等
  • 比较的基础是方差比
  • 如果系统(处理)误差显著地不同于随机误差，则均值就是不相等的；反之，均值就是相等的

随机误差：

  • 因素的同一水平(总体)下，样本各观察值之间的差异

  • 比如，同一行业下不同企业被投诉次数是不同的

  • 这种差异可以看成是随机因素的影响，称为随机误差

系统误差：

  • 因素的不同水平(不同总体)下，各观察值之间的差异
  • 比如，不同行业之间的被投诉次数之间的差异
  • 这种差异可能是由于抽样的随机性所造成的，也可能是由于行业本身所造成的，后者所形成的误差是由系统性因素造成的，称为系统误差

组内方差：

  • 因素的同一水平(同一个总体)下样本数据的方差
  • 比如，零售业被投诉次数的方差
  • 组内方差只包含随机误差

组间方差：

  • 因素的不同水平(不同总体)下各样本之间的方差
  • 比如，四个行业被投诉次数之间的方差
  • 组间方差既包括随机误差，也包括系统误差

方差的比较：

  • 若不同行业对投诉次数没有影响，则组间误差中只包含随机误差，没有系统误差。这时，组间误差与组内误差经过平均后的数值就应该很接近，它们的比值就会接近1

  • 若不同行业对投诉次数有影响，在组间误差中除了包含随机误差外，还会包含有系统误差，这时组间误差平均后的数值就会大于组内误差平均后的数值，它们之间的比值就会大于1

  • 这个比值大到某种程度时，就可以说不同水平之间存在着显著差异，也就是自变量对因变量有影响

  • 判断行业对投诉次数是否有显著影响，实际上也就是检验被投诉次数的差异主要是由于什么原因所引起的。如果这种差异主要是系统误差，说明不同行业对投诉次数有显著影响

方差分析的前提：

每个总体都应服从正态分布

  • 对于因素的每一个水平，其观察值是来自服从正态分布总体的简单随机样本
  • 比如，每个行业被投诉的次数必需服从正态分布

各个总体的方差必须相同

  • 各组观察数据是从具有相同方差的总体中抽取的
  • 比如，四个行业被投诉次数的方差都相等

观察值是独立的

  • 比如，每个行业被投诉的次数与其他行业被投诉的次数独立

在上述假定条件下，判断行业对投诉次数是否有显著影响，实际上也就是检验具有同方差的四个正态总体的均值是否相等

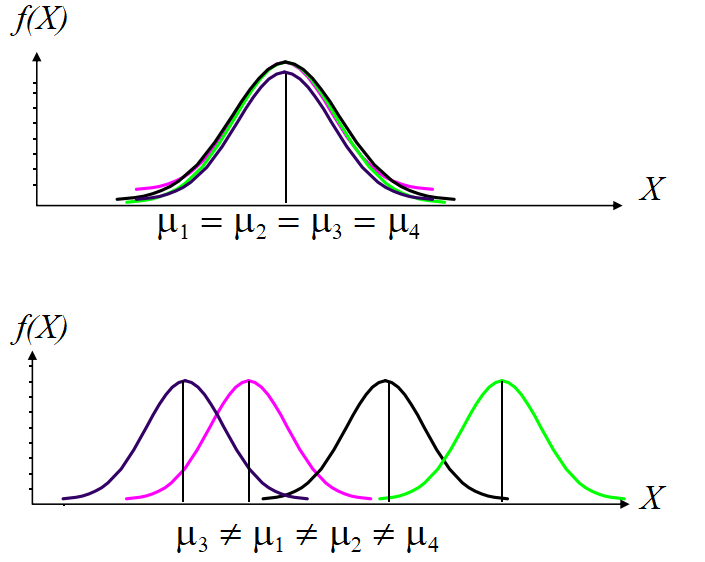
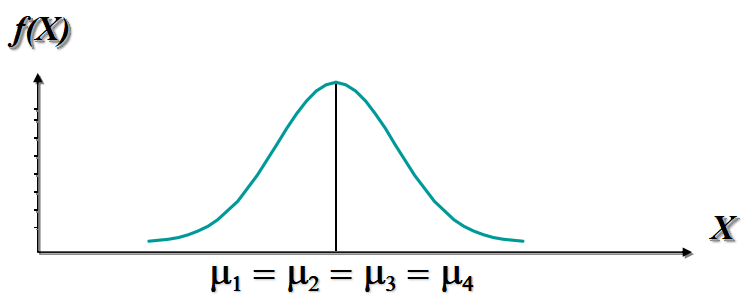
原假设成立，即H0: μ1 = μ2 = μ3 = μ4

  • 四个行业被投诉次数的均值都相等意味着每个样本都来自均值为μ、方差为σ^2的同一正态总体
variance7

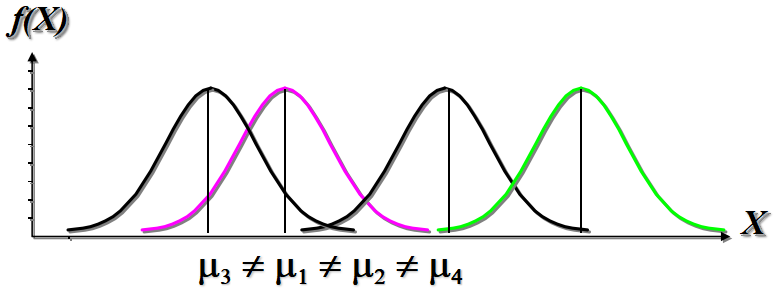
备择假设成立，即H1: μ1 μ2 μ3 μ4 不完全相等

  • 至少有一个总体的均值是不同的,四个样本分别来自均值不同的四个正态总体
variance8

单因素方差分析

  • 模型中有一个自变量（因素）和一个观测变量,其实就是关于在一个影响因素的不同水平下，观测变量均值差异的显著性检验。
variance9

提出假设：

  • H0: μ1 = μ2 = 。。。 =μk ，自变量对因变量没有显著影响
  • 即H1: μ1 μ2 。。。μ4 不完全相等， 自变量对因变量有显著影响

拒绝原假设，只表明至少有两个总体的均值不相等，并不意味着所有的均值都不相等

检验的统计量

  • 水平的均值
  • 全部观察值的总均值
  • 误差平方和
  • 均方(MS)

水平的均值：

假定从第i个总体中抽取一个容量为ni的简单随机样本，第i个总体的样本均值为该样本的全部观察值总和除以观察值的个数
variance10

全部观察值的总均值：

全部观察值的总和除以观察值的总个数

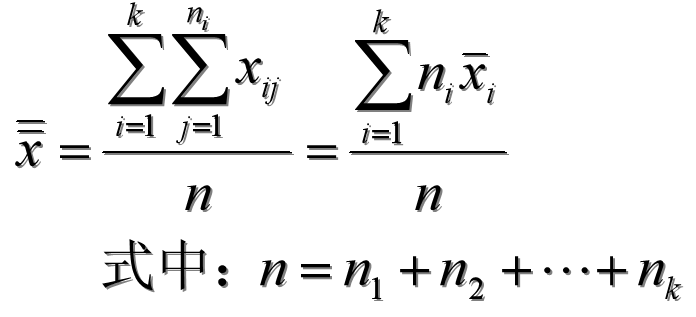
variance11

均值计算结果






总误差平方和 SST：

全部观察值与总平均值的离差平方和，反映全部观察值的离散状况




水平项平方和 SSA

各组平均值与总平均值的离差平方和，反映各总体的样本均值之间的差异程度，又称组间平方和，该平方和既包括随机误差，也包括系统误差



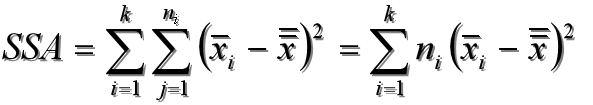
误差项平方和 SSE

每个水平或组的各样本数据与其组平均值的离差平方和，反映每个样本各观察值的离散状况，又称组内平方和，该平方和反映的是随机误差的大小



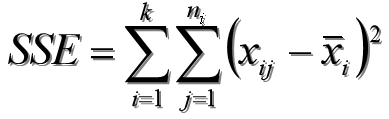
平方和之间的关系

总离差平方和(SST)、误差项离差平方和(SSE)、水平项离差平方和 (SSA) 之间的关系





SST反映全部数据总的误差程度；SSE反映随机误差的大小；SSA反映随机误差和系统误差的大小

如果原假设成立，则表明没有系统误差，组间平方和SSA除以自由度后的均方与组内平方和SSE和除以自由度后的均方差异就不会太大；如果组间均方显著地大于组内均方，说明各水平(总体)之间的差异不仅有随机误差，还有系统误差，判断因素的水平是否对其观察值有影响，实际上就是比较组间方差与组内方差之间差异的大小

均方MS

各误差平方和的大小与观察值的多少有关，为消除观察值多少对误差平方和大小的影响，需要将其平均，这就是均方，也称为方差，计算方法是用误差平方和除以相应的自由度

各自自由度

  • SST 的自由度为n-1，其中n为全部观察值的个数

  • SSA的自由度为k-1，其中k为因素水平(总体)的个数

  • SSE 的自由度为n-k

F统计量

将MSA（组间方差，SSA的均方，记为MSA）和MSE（组内方差，SSE的均方，记为MSE）进行对比，即得到所需要的检验统计量F







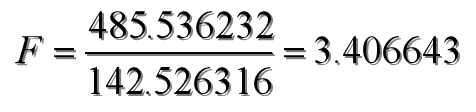
根据给定的显著性水平，在F分布表中查找与第一自由度df1＝k-1、第二自由度df2=n-k 相应的临界值

  • 若F>Fα ，则拒绝原假设H0 ，表明均值之间的差异是显著的，所检验的因素对观察值有显著影响
  • 若F<Fα ，则不拒绝原假设H0 ，不能认为所检验的因素对观察值有显著影响

方差分析表：





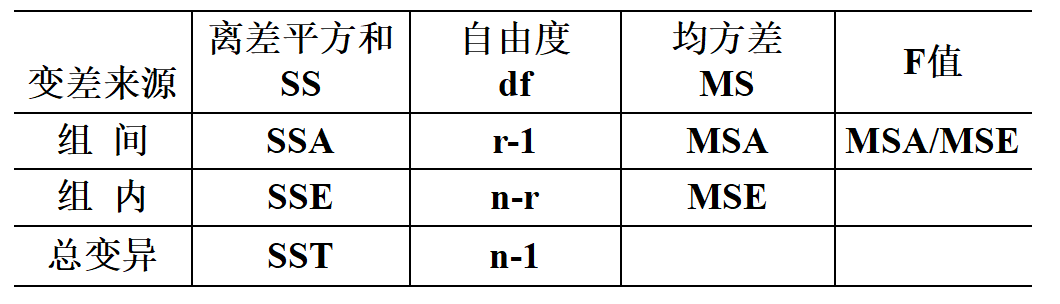
实例：
在评价某药物耐受性及安全性的I期临床试验中，对符合纳入标准的30名健康自愿者随机分为3组每组10名，各组注射剂量分别为0.5U、1U、2U，观察48小时部分凝血活酶时间（s）试问不同剂量的部分凝血活酶时间有无不同？







提出假设： H0:μ1=μ2=μ3 H1:μ1，μ2，μ3不全相同 显著水平a=0.05





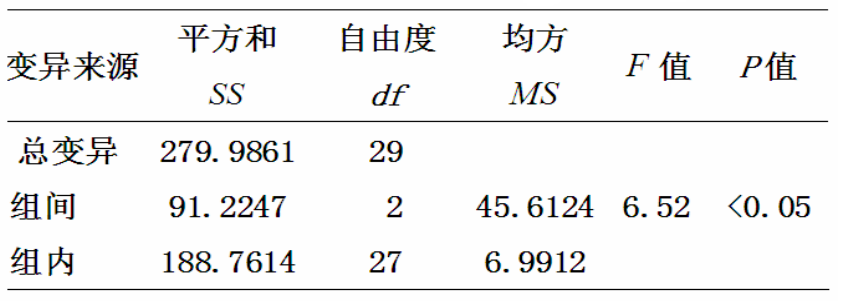
- F0.05(2，26) =2.52，F>F0.05(2，26) ，P<0.05 - 拒绝 H0。 三种不同剂量48小时部分凝血活酶时间不全相同。

方差分析中的多重比较

  • 通过对总体均值之间的配对比较来进一步检验到底哪些均值之间存在差异

  • 可采用Fisher提出的最小显著差异方法，简写为LSD

  • LSD方法是对检验两个总体均值是否相等的t检验方法的总体方差估计而得到的

LSD方法：

对k组中的两组的平均数进行比较，当两组样本容量分别为ni,nj都为时，有





实例：颜色对销售额的影响







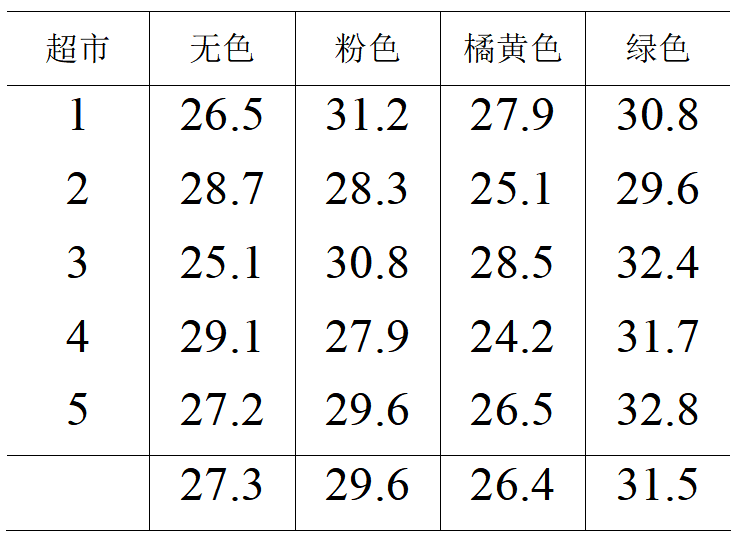
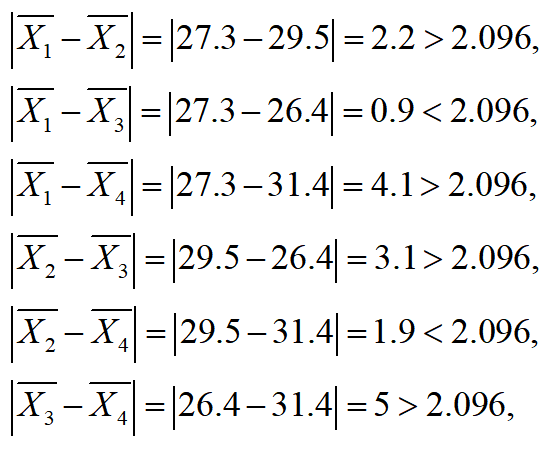
依据上局结果可得出影响效果

多因素方差分析

  • 无交互效应的多因素方差分析
  • 有交互效应的多因素方差分析

主效应与交互效应

  • 主效应（main effect）：各个因素对观测变量的单独影响称为主效应。
  • 交互效应（interaction effect）：各个因素不同水平的搭配所产生的新的影响称为交互效应。

双因素方差分析的类型

  • 双因素方差分析中因素A和B对结果的影响相互独立时称为无交互效应的双因素方差分析。
  • 如果除了A和B对结果的单独影响外还存在交互效应，这时的双因素方差分析称为有交互效应的双因素方差分析 。

无交互效应的双因素方差分析模型

  • 离差平方和的分解：






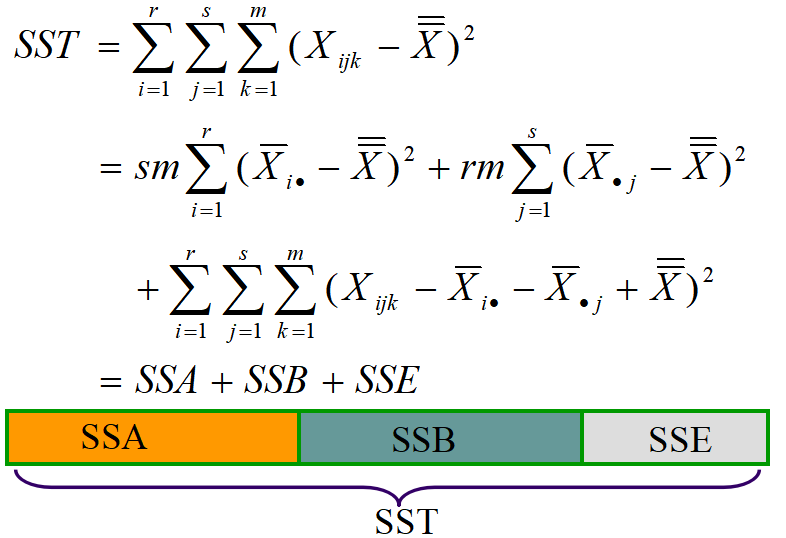
有交互效应的双因素方差分析模型

  • 离差平方和的分解:








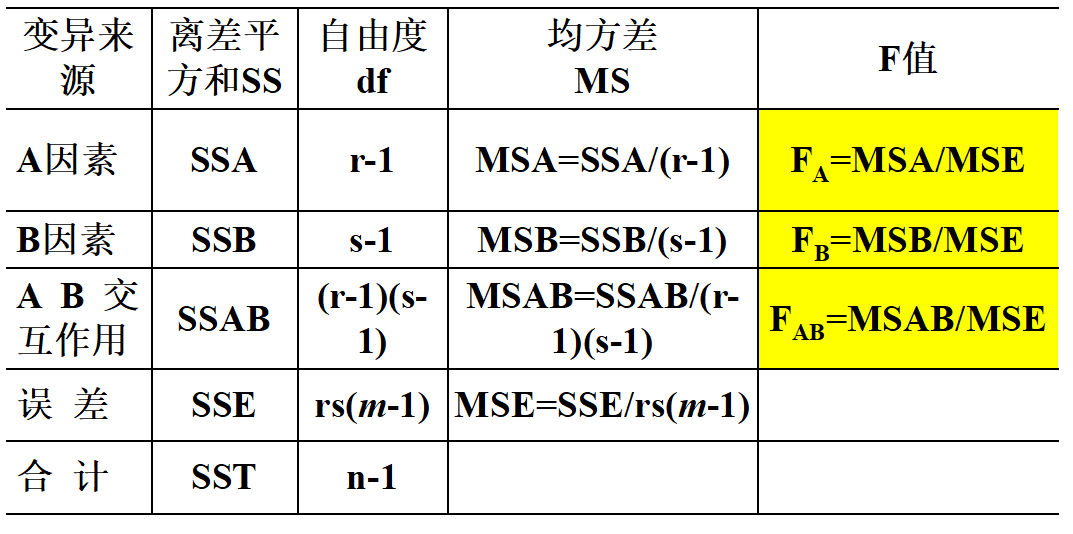
双因素方差分析的步骤

提出假设

  • 要说明因素A有无显著影响，就是检验如下假设：

H0：因素A不同水平下观测变量的总体均值无显著差异。

H1：因素A不同水平下观测变量的总体均值存在显著差异。

  • 要说明因素B有无显著影响，就是检验如下假设：

H0：因素B不同水平下观测变量的总体均值无显著差异。

H1：因素B不同水平下观测变量的总体均值存在显著差异。

  • 在有交互效应的双因素方差中，要说明两个因素的交互效应是否显著，还要检验第三组零假设和备择假设：

H0：因素A和因素B的交互效应对观测变量的总体均值无显著差异。

H1：因素A和因素B的交互效应对观测变量的总体均值存在显著差异。

构造统计量

在原假设成立的情况下，三个统计量分别服从自由度为（r-1,rs(m-1)）、（s-1,rs(m-1)）、（(r-1)(s-1),rs(m-1)）的F分布。



利用原假设和样本数据分别计算3个F统计量的值和其对应的p值,对比p值和α，结合原假设作出推断。若p<α，则拒绝关于这个因素的原假设，得出此因素不同水平下观测变量各总体均值存在显著差异的结论。

实例：
有四个品牌的彩电在五个地区销售，为分析彩电的品牌(品牌因素)和销售地区(地区因素)对销售量是否有影响，对每个品牌在各地区的销售量取得以下数据。试分析品牌和销售地区对彩电的销售量是否有显著影响？(α=0.05)







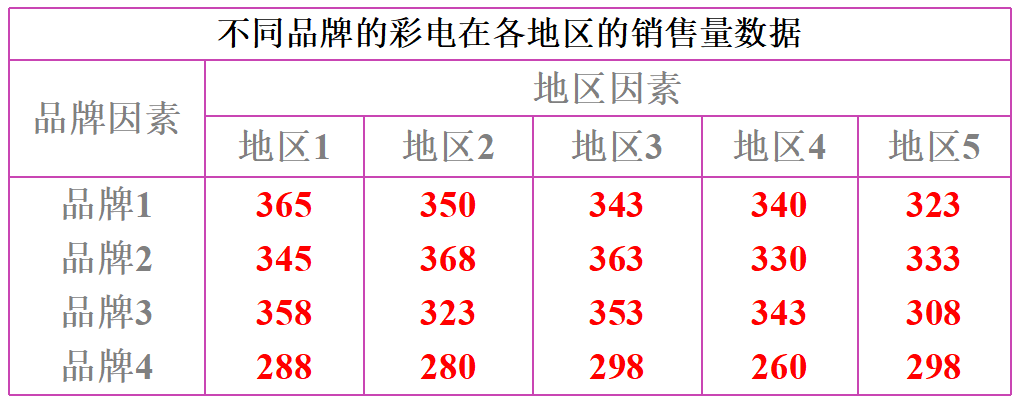
提出假设：

  • 对行因素提出的假设为：

H0: μ1 = μ2 = … = μi = …= μk (μi为第i个水平的均值)
H1: μi (i =1,2, … , k) 不全相等

  • 对列因素提出的假设为：

H0: μ1 = μ2 = … = μj = …= μr (mj为第j个水平的均值)
H1: μj (j =1,2,…,r) 不全相等

计算各平方和





计算均方

误差平方和除以相应的自由度

  • 总离差平方和SST的自由度为 kr-1
  • 行因素的离差平方和SSR的自由度为 k-1
  • 列因素的离差平方和SSC的自由度为 r-1
  • 随机误差平方和SSE的自由度为 (k-1)×(r-1)

计算检验统计量(F)

  • 计算检验统计量(F)


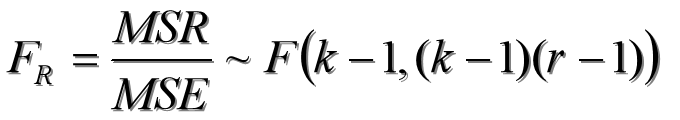
  • 检验列因素的统计量




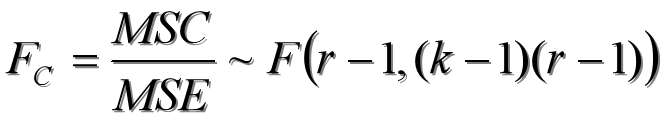
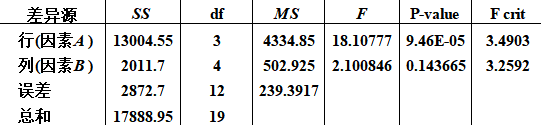
FA＝18.10777>Fα＝3.4903，拒绝原假设H0，说明彩电的品牌对销售量有显著影响

FB＝2.100846< Fα＝3.2592，接受原假设H0，说明销售地区对彩电的销售量没有显著影响

posted @ 2022-03-08 13:36  9~  阅读(1226)  评论(0)  编辑  收藏  举报