因子分析-降维算法LDA/PCA
因子分析-降维算法LDA/PCA
因子分析是将具有错综复杂关系的变量(或样本)综合为少数几个因子,以再现原始变量和因子之间的相互关系,探讨多个能够直接测量,并且具有一定相关性的实测指标是如何受少数几个内在的独立因子所支配,并且在条件许可时借此尝试对变量进行分类。
因子分析的基本思想
根据变量间相关性的大小把变量分组,使得同组内的变量之间的相关性(共性)较高,并用一个公共因子来代表这个组的变量,而不同组的变量相关性较低(个性)。
因子分析的目的
因子分析的目的,通俗来讲就是简化变量维数。即要使因素结构简单化,希望以最少的共同因素(公共因子),能对总变异量作最大的解释,因而抽取得因子越少越好,但抽取的因子的累积解释的变异量越大越好。
主要内容:
(1):主成分分析PCA
(2):线性判别分析LDA
线性判别分析LDA(Linear Discriminant Analysis)
LCA主要用于数据预处理中的降维,分类任务。LCA关心的是能够最大化类间区分度的坐标轴成分,将特征空间(数据集中的多维样本)投影到一个维度更小的k 维子空间中,同时保持区分类别的信息。其原理是投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近方法。与PCA不同,LDA更关心分类而不是方差。
- LDA分类的一个目标是使得不同类别之间的距离越远越好,同一类别之中的距离越近越好
- 每类样例的均值:
![image-20220308102350539]()
- 投影后的均值:
![image-20220308102407195]()
- 投影后的两类样本中心点尽量分离:
![image-20220308102422910]()
散列值:样本点的密集程度,值越大,越分散,反之,越集中。
同类之间应该越密集些: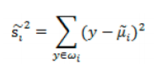
- 目标函数:
![image-20220308110450622]()
- 散列值公式展开:
![image-20220308110504676]()
- 散列矩阵(scatter matrices):
![image-20220308110540622]()
- 类内散布矩阵𝑆𝐵:
![image-20220308110613948]()
- 分子展开:
![image-20220308110437585]()
- 最终目标函数:
![image-20220308110422659]()
- 分母进行归一化:如果分子、分母是都可以取任意值的,那就会使得有无穷解,我们将分母限制为长度为1
- 拉格朗日乘子法:
![image-20220308110714010]()
- 两边都乘以Sw的逆:
![image-20220308110804839]()
feature_dict = {i:label for i,label in zip(
range(4),
('sepal length in cm',
'sepal width in cm',
'petal length in cm',
'petal width in cm', ))}
import pandas as pd
df = pd.io.parsers.read_csv(
filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
header=None,
sep=',',
)
df.columns = [l for i,l in sorted(feature_dict.items())] + ['class label']
df.dropna(how="all", inplace=True) # to drop the empty line at file-end
df.tail()
sepal length in cm sepal width in cm petal length in cm petal width in cm class label 145 6.7 3.0 5.2 2.3 Iris-virginica 146 6.3 2.5 5.0 1.9 Iris-virginica 147 6.5 3.0 5.2 2.0 Iris-virginica 148 6.2 3.4 5.4 2.3 Iris-virginica 149 5.9 3.0 5.1 1.8 Iris-virginica

from sklearn.preprocessing import LabelEncoder
X = df[['sepal length in cm','sepal width in cm','petal length in cm','petal width in cm']].values
y = df['class label'].values
enc = LabelEncoder()
label_encoder = enc.fit(y)
y = label_encoder.transform(y) + 1
#label_dict = {1: 'Setosa', 2: 'Versicolor', 3:'Virginica'}
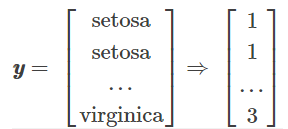
分别求三种鸢尾花数据在不同特征维度上的均值向量 mi

import numpy as np
np.set_printoptions(precision=4)
mean_vectors = []
for cl in range(1,4):
mean_vectors.append(np.mean(X[y==cl], axis=0))
print('Mean Vector class %s: %s\n' %(cl, mean_vectors[cl-1]))
Mean Vector class 1: [ 5.006 3.418 1.464 0.244] Mean Vector class 2: [ 5.936 2.77 4.26 1.326] Mean Vector class 3: [ 6.588 2.974 5.552 2.026]
计算两个 4×4 维矩阵:类内散布矩阵和类间散布矩阵
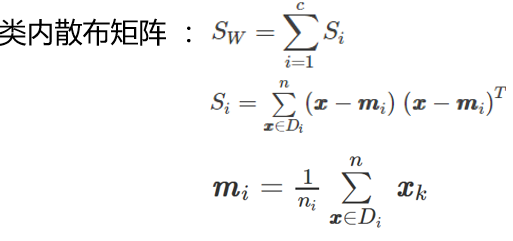
S_W = np.zeros((4,4))
for cl,mv in zip(range(1,4), mean_vectors):
class_sc_mat = np.zeros((4,4)) # scatter matrix for every class
for row in X[y == cl]:
row, mv = row.reshape(4,1), mv.reshape(4,1) # make column vectors
class_sc_mat += (row-mv).dot((row-mv).T)
S_W += class_sc_mat # sum class scatter matrices
print('within-class Scatter Matrix:\n', S_W)
S_W = np.zeros((4,4))
for cl,mv in zip(range(1,4), mean_vectors):
class_sc_mat = np.zeros((4,4)) # scatter matrix for every class
for row in X[y == cl]:
row, mv = row.reshape(4,1), mv.reshape(4,1) # make column vectors
class_sc_mat += (row-mv).dot((row-mv).T)
S_W += class_sc_mat # sum class scatter matrices
print('within-class Scatter Matrix:\n', S_W)
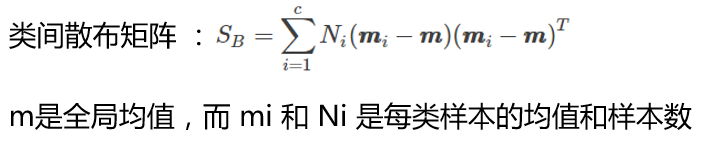
overall_mean = np.mean(X, axis=0)
S_B = np.zeros((4,4))
for i,mean_vec in enumerate(mean_vectors):
n = X[y==i+1,:].shape[0]
mean_vec = mean_vec.reshape(4,1) # make column vector
overall_mean = overall_mean.reshape(4,1) # make column vector
S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
print('between-class Scatter Matrix:\n', S_B)
between-class Scatter Matrix: [[ 63.2121 -19.534 165.1647 71.3631] [ -19.534 10.9776 -56.0552 -22.4924] [ 165.1647 -56.0552 436.6437 186.9081] [ 71.3631 -22.4924 186.9081 80.6041]]

eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
for i in range(len(eig_vals)):
eigvec_sc = eig_vecs[:,i].reshape(4,1)
print('\nEigenvector {}: \n{}'.format(i+1, eigvec_sc.real))
print('Eigenvalue {:}: {:.2e}'.format(i+1, eig_vals[i].real))
Eigenvector 1:
[[ 0.2049]
[ 0.3871]
[-0.5465]
[-0.7138]]
Eigenvalue 1: 3.23e+01
Eigenvector 2:
[[-0.009 ]
[-0.589 ]
[ 0.2543]
[-0.767 ]]
Eigenvalue 2: 2.78e-01
Eigenvector 3:
[[-0.7113]
[ 0.0353]
[-0.0267]
[ 0.7015]]
Eigenvalue 3: -5.76e-15
Eigenvector 4:
[[ 0.422 ]
[-0.4364]
[-0.4851]
[ 0.6294]]
Eigenvalue 4: 7.80e-15
特征值与特征向量:
- 特征向量:表示映射方向
- 特征值:特征向量的重要程度
#Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in decreasing order:\n')
for i in eig_pairs:
print(i[0])
Eigenvalues in decreasing order:
32.2719577997
0.27756686384
7.7995841654e-15
5.76433252705e-15
print('Variance explained:\n')
eigv_sum = sum(eig_vals)
for i,j in enumerate(eig_pairs):
print('eigenvalue {0:}: {1:.2%}'.format(i+1, (j[0]/eigv_sum).real))
Variance explained:
eigenvalue 1: 99.15%
eigenvalue 2: 0.85%
eigenvalue 3: 0.00%
eigenvalue 4: 0.00%
W = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))
print('Matrix W:\n', W.real)
Matrix W:
[[ 0.2049 -0.009 ]
[ 0.3871 -0.589 ]
[-0.5465 0.2543]
[-0.7138 -0.767 ]]
X_lda = X.dot(W)
assert X_lda.shape == (150,2), "The matrix is not 150x2 dimensional."
from matplotlib import pyplot as plt
def plot_step_lda():
ax = plt.subplot(111)
for label,marker,color in zip(
range(1,4),('^', 's', 'o'),('blue', 'red', 'green')):
plt.scatter(x=X_lda[:,0].real[y == label],
y=X_lda[:,1].real[y == label],
marker=marker,
color=color,
alpha=0.5,
label=label_dict[label]
)
plt.xlabel('LD1')
plt.ylabel('LD2')
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title('LDA: Iris projection onto the first 2 linear discriminants')
# hide axis ticks
plt.tick_params(axis="both", which="both", bottom="off", top="off",
labelbottom="on", left="off", right="off", labelleft="on")
# remove axis spines
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.spines["left"].set_visible(False)
plt.grid()
plt.tight_layout
plt.show()
plot_step_lda()
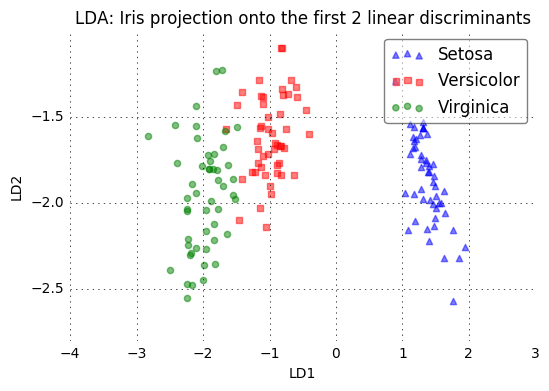
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
# LDA
sklearn_lda = LDA(n_components=2)
X_lda_sklearn = sklearn_lda.fit_transform(X, y)
def plot_scikit_lda(X, title):
ax = plt.subplot(111)
for label,marker,color in zip(
range(1,4),('^', 's', 'o'),('blue', 'red', 'green')):
plt.scatter(x=X[:,0][y == label],
y=X[:,1][y == label] * -1, # flip the figure
marker=marker,
color=color,
alpha=0.5,
label=label_dict[label])
plt.xlabel('LD1')
plt.ylabel('LD2')
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
# hide axis ticks
plt.tick_params(axis="both", which="both", bottom="off", top="off",
labelbottom="on", left="off", right="off", labelleft="on")
# remove axis spines
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.spines["left"].set_visible(False)
plt.grid()
plt.tight_layout
plt.show()
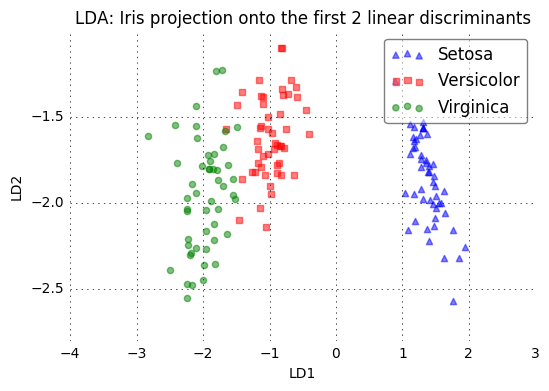
plot_step_lda()
plot_scikit_lda(X_lda_sklearn, title='Default LDA via scikit-learn')
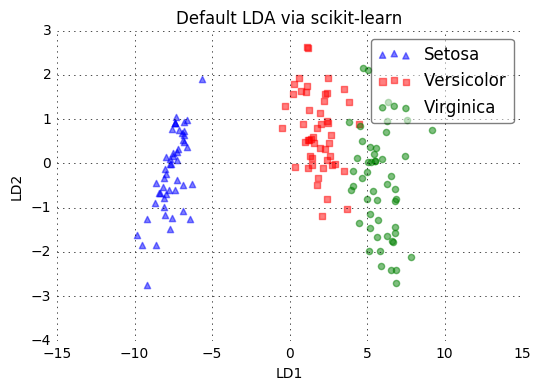
主成分分析PCA(Principal Component Analysis)
PCA是降维中最常用的一种手段,提取最有价值的信息(基于方差)。
向量的表示:
- 内积:
![image-20220308115212486]()
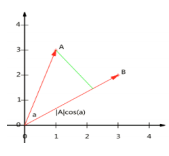
- 解释:
![image-20220308115203677]()
- 设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度
![image-20220308115154425]()
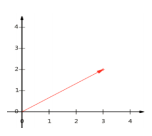
- 向量可以表示为(3,2)实际上表示线性组合:
![image-20220308115106877]()
![image-20220308115056099]()
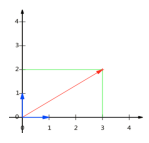
- 基:(1,0)和(0,1)叫做二维空间中的一组基
![image-20220308115022287]()
基变换:
- 基是正交的(即内积为0,或直观说相互垂直)。要求:线性无关
![image-20220308114947251]()
- 变换:数据与一个基做内积运算,结果作为第一个新的坐标分量,然后与第二个基做内积运算,结果作为第二个新坐标的分量
- 数据(3,2)映射到基中坐标:
![image-20220308114850816]()
- 两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去:
![image-20220308114839207]()
协方差矩阵:
- 方向:如何选择这个方向(或者说基)才能尽量保留最多的原始信息呢?一种直观的看法是:希望投影后的投影值尽可能分散
- 方差:
![image-20220308114824871]()
- 寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大
- 协方差(假设均值为0时):
![image-20220308114810825]()
协方差:
- 如果单纯只选择方差最大的方向,后续方向应该会和方差最大的方向接近重合。
- 解决方案:为了让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的
- 协方差:可以用两个字段的协方差表示其相关性
![image-20220308114754745]()
- 当协方差为0时,表示两个字段完全独立。为了让协方差为0,选择第二个基时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。
优化目标:
- 将一组N维向量降为K维(K大于0,小于N),目标是选择K个单位正交基,使原始数据变换到这组基上后,各字段两两间协方差为0,字段的方差则尽可能大
- 协方差矩阵:
![image-20220308114731170]()
- 矩阵对角线上的两个元素分别是两个字段的方差,而其它元素是a和b的协方差。
- 协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上将元素按大小从上到下排列
- 协方差矩阵对角化:
![image-20220308114715950]()
- 实对称矩阵:一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量:
![image-20220308114652697]()
- 实对称阵可进行对角化:
![image-20220308114638996]()
- 根据特征值的从大到小,将特征向量从上到下排列,则用前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要的降维后的数据矩阵Y
PCA实例:
数据:
协方差矩阵: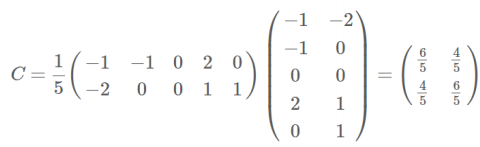
特征值: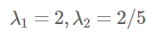
特征向量: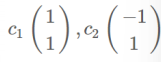
对角化: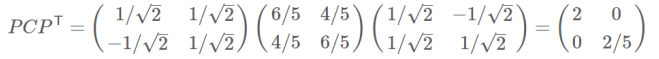
降维: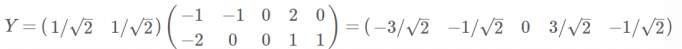
import numpy as np
import pandas as pd
df = pd.read_csv('iris.data')
df.head()
5.1 3.5 1.4 0.2 Iris-setosa 0 4.9 3.0 1.4 0.2 Iris-setosa 1 4.7 3.2 1.3 0.2 Iris-setosa 2 4.6 3.1 1.5 0.2 Iris-setosa 3 5.0 3.6 1.4 0.2 Iris-setosa 4 5.4 3.9 1.7 0.4 Iris-setosa
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
df.head()
sepal_len sepal_wid petal_len petal_wid class 0 4.9 3.0 1.4 0.2 Iris-setosa 1 4.7 3.2 1.3 0.2 Iris-setosa 2 4.6 3.1 1.5 0.2 Iris-setosa 3 5.0 3.6 1.4 0.2 Iris-setosa
# split data table into data X and class labels y
X = df.ix[:,0:4].values
y = df.ix[:,4].values
from matplotlib import pyplot as plt
import math
label_dict = {1: 'Iris-Setosa',
2: 'Iris-Versicolor',
3: 'Iris-Virgnica'}
feature_dict = {0: 'sepal length [cm]',
1: 'sepal width [cm]',
2: 'petal length [cm]',
3: 'petal width [cm]'}
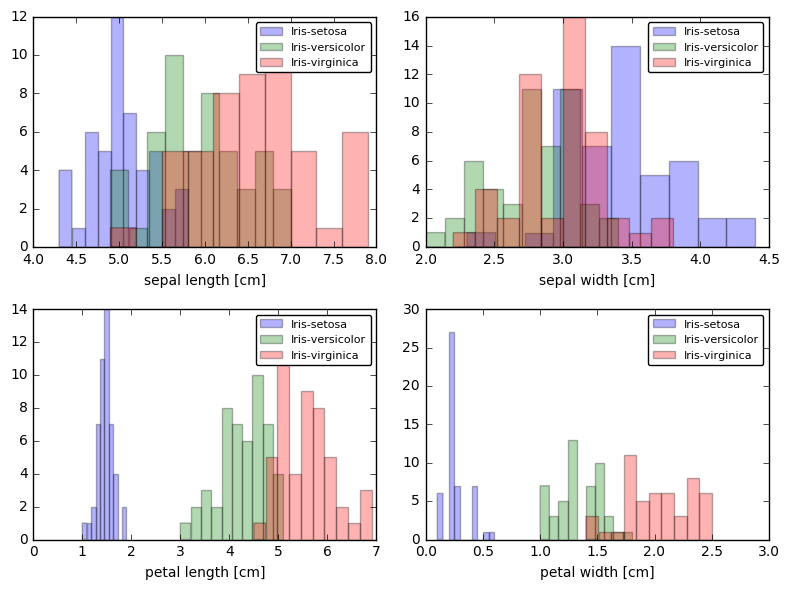
plt.figure(figsize=(8, 6))
for cnt in range(4):
plt.subplot(2, 2, cnt+1)
for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
plt.hist(X[y==lab, cnt],
label=lab,
bins=10,
alpha=0.3,)
plt.xlabel(feature_dict[cnt])
plt.legend(loc='upper right', fancybox=True, fontsize=8)
plt.tight_layout()
plt.show()
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
print (X_std)
Output exceeds the size limit. Open the full output data in a text editor
[[-1.1483555 -0.11805969 -1.35396443 -1.32506301] [-1.3905423 0.34485856 -1.41098555 -1.32506301] [-1.51163569 0.11339944 -1.29694332 -1.32506301] [-1.02726211 1.27069504 -1.35396443 -1.32506301] [-0.54288852 1.9650724 -1.18290109 -1.0614657 ] [-1.51163569 0.8077768 -1.35396443 -1.19326436] [-1.02726211 0.8077768 -1.29694332 -1.32506301] [-1.75382249 -0.34951881 -1.35396443 -1.32506301] [-1.1483555 0.11339944 -1.29694332 -1.45686167] [-0.54288852 1.50215416 -1.29694332 -1.32506301] [-1.2694489 0.8077768 -1.23992221 -1.32506301] [-1.2694489 -0.11805969 -1.35396443 -1.45686167] [-1.87491588 -0.11805969 -1.52502777 -1.45686167] [-0.05851493 2.19653152 -1.46800666 -1.32506301] [-0.17960833 3.122368 -1.29694332 -1.0614657 ] [-0.54288852 1.9650724 -1.41098555 -1.0614657 ] [-0.90616871 1.03923592 -1.35396443 -1.19326436] [-0.17960833 1.73361328 -1.18290109 -1.19326436] [-0.90616871 1.73361328 -1.29694332 -1.19326436] [-0.54288852 0.8077768 -1.18290109 -1.32506301] [-0.90616871 1.50215416 -1.29694332 -1.0614657 ] [-1.51163569 1.27069504 -1.58204889 -1.32506301] [-0.90616871 0.57631768 -1.18290109 -0.92966704] [-1.2694489 0.8077768 -1.06885886 -1.32506301] [-1.02726211 -0.11805969 -1.23992221 -1.32506301]
[ 1.03132564 -0.11805969 0.81283789 1.4427088 ] [ 0.54695205 -1.27535529 0.69879566 0.91551417] [ 0.78913885 -0.11805969 0.81283789 1.04731282] [ 0.42585866 0.8077768 0.92688012 1.4427088 ] [ 0.06257847 -0.11805969 0.75581678 0.78371551]]
mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
print('Covariance matrix \n%s' %cov_mat)
Covariance matrix [[ 1.00675676 -0.10448539 0.87716999 0.82249094] [-0.10448539 1.00675676 -0.41802325 -0.35310295] [ 0.87716999 -0.41802325 1.00675676 0.96881642] [ 0.82249094 -0.35310295 0.96881642 1.00675676]]
print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))
NumPy covariance matrix: [[ 1.00675676 -0.10448539 0.87716999 0.82249094] [-0.10448539 1.00675676 -0.41802325 -0.35310295] [ 0.87716999 -0.41802325 1.00675676 0.96881642] [ 0.82249094 -0.35310295 0.96881642 1.00675676]]
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
print('Eigenvectors \n%s' %eig_vecs)
print('\nEigenvalues \n%s' %eig_vals)
Eigenvectors [[ 0.52308496 -0.36956962 -0.72154279 0.26301409] [-0.25956935 -0.92681168 0.2411952 -0.12437342] [ 0.58184289 -0.01912775 0.13962963 -0.80099722] [ 0.56609604 -0.06381646 0.63380158 0.52321917]]
Eigenvalues [ 2.92442837 0.93215233 0.14946373 0.02098259]
# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print (eig_pairs)
print ('----------')
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i[0])
[(2.9244283691111144, array([ 0.52308496, -0.25956935, 0.58184289, 0.56609604])), (0.93215233025350641, array([-0.36956962, -0.92681168, -0.01912775, -0.06381646])), (0.14946373489813314, array([-0.72154279, 0.2411952 , 0.13962963, 0.63380158])), (0.020982592764270606, array([ 0.26301409, -0.12437342, -0.80099722, 0.52321917]))]
----------
Eigenvalues in descending order:
2.92442836911
0.932152330254
0.149463734898
0.0209825927643
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
print (var_exp)
cum_var_exp = np.cumsum(var_exp)
cum_var_exp
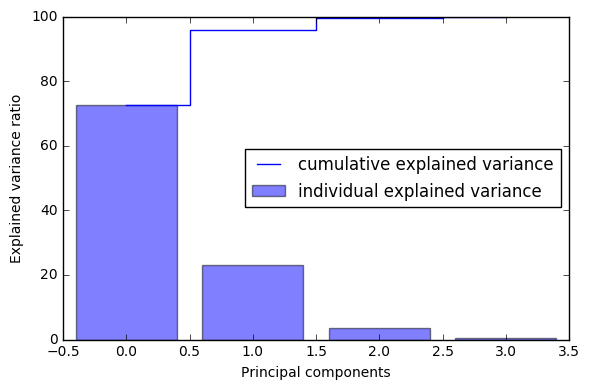
[72.620033326920336, 23.147406858644135, 3.7115155645845164, 0.52104424985101538]
array([ 72.62003333, 95.76744019, 99.47895575, 100. ])
a = np.array([1,2,3,4])
print (a)
print ('-----------')
print (np.cumsum(a))
[1 2 3 4]
-----------
[ 1 3 6 10]
plt.figure(figsize=(6, 4))
plt.bar(range(4), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
eig_pairs[1][1].reshape(4,1)))
print('Matrix W:\n', matrix_w)
Matrix W:
[[ 0.52308496 -0.36956962]
[-0.25956935 -0.92681168]
[ 0.58184289 -0.01912775]
[ 0.56609604 -0.06381646]]
Y = X_std.dot(matrix_w)
Y
Output exceeds the size limit. Open the full output data in a text editor
array([[-2.10795032, 0.64427554], [-2.38797131, 0.30583307], [-2.32487909, 0.56292316], [-2.40508635, -0.687591 ], [-2.08320351, -1.53025171], [-2.4636848 , -0.08795413], [-2.25174963, -0.25964365], [-2.3645813 , 1.08255676], [-2.20946338, 0.43707676], [-2.17862017, -1.08221046], [-2.34525657, -0.17122946], [-2.24590315, 0.6974389 ], [-2.66214582, 0.92447316], [-2.2050227 , -1.90150522], [-2.25993023, -2.73492274], [-2.21591283, -1.52588897], [-2.20705382, -0.52623535], [-1.9077081 , -1.4415791 ], [-2.35411558, -1.17088308], [-1.93202643, -0.44083479], [-2.21942518, -0.96477499], [-2.79116421, -0.50421849], [-1.83814105, -0.11729122], [-2.24572458, -0.17450151], [-1.97825353, 0.59734172],
[ 1.99464025, -1.04517619], [ 1.85977129, -0.37934387], [ 1.54200377, 0.90808604], [ 1.50925493, -0.26460621], [ 1.3690965 , -1.01583909], [ 0.94680339, 0.02182097]])
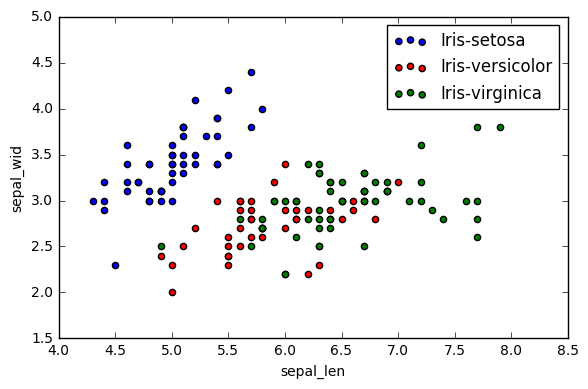
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(X[y==lab, 0],
X[y==lab, 1],
label=lab,
c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
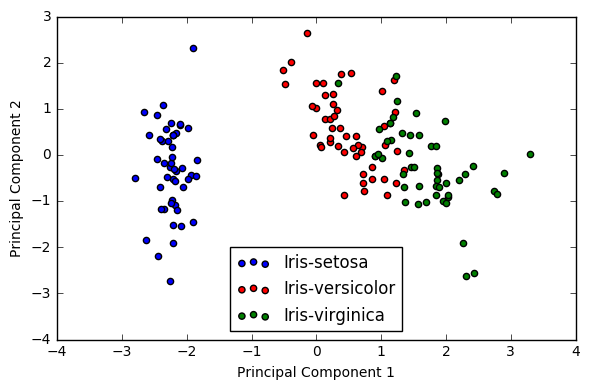
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y[y==lab, 0],
Y[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()

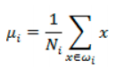
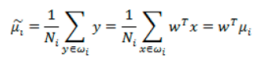
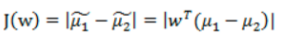
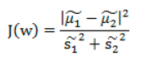
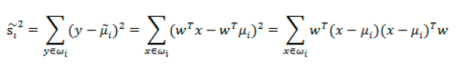
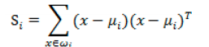
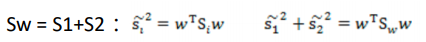
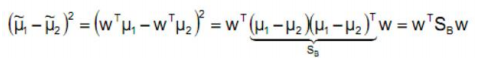
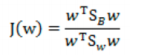
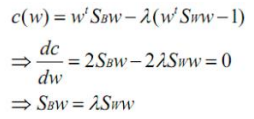

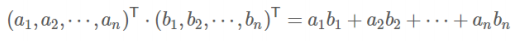

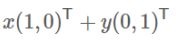
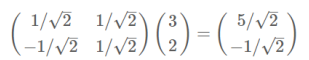
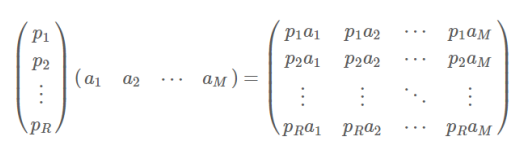
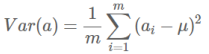
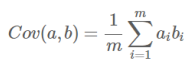
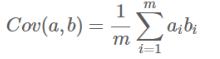
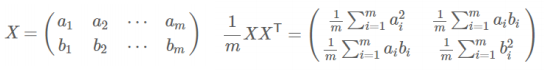
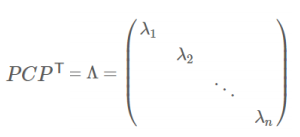
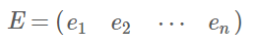
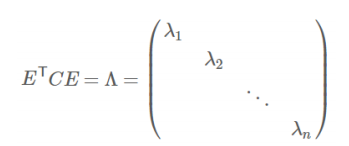

 浙公网安备 33010602011771号
浙公网安备 33010602011771号