6.1 机器学习之数学基础

机器学习之数学基础[1][2][3][4]

基础概念

极限

  • 对于数列 $ { u_n} $，如果当n无限增大时，其通项无限接近于一个常数A，则称该数列以A为称数列收敛于A，否则称数列为发散。

    $ {\lim\limits_{n\to\infty}u_n = A}，或 \quad u_n\rightarrow A ,(n\rightarrow\infty) $

  • $ \lim\limits_{x\to x_0} f(x) = A 的充要条件是\lim\limits_{x\to x_0^-} f(x) = \lim\limits_{x\to x_0^+} f(x) = A $

导数

  • 如果平均变化率的极限存在，

\[\lim\limits_{\Delta x\to0} \frac{\Delta y}{\Delta x} = \lim\limits_{\Delta x\to0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}， \]

则称此极限为函数y=f(x)在点x_0处的导数，

\[f^\prime(x_0)，y^\prime \mid _{x=x_0}, \left. \frac{{\rm d}f(x)}{{\rm d}x} \right | _{x=x_0} \]

​ image-20220221180028466

梯度

偏导数

  • 设函数z=f(x,y)在点(x0, y0)的某个领域内有定义，对于y=y0，一元函数f(x, y0)在点x=x0处可导，即极限

\[\lim\limits_{\Delta x\to0} \frac{f(x_0+\Delta x, y_0)-f(x_0,y_0)}{\Delta x}=A， \]

则称A为函数：$ z=f(x,y)在点(x_0,y_0)处关于自变量X的偏导数，记作： $

\[f_x(x_0, y_0) \quad 或者 \quad \left. \frac{\partial z}{\partial x} \right | _{\substack{x=x_0 \\ y=y_0}}，\left. \frac{\partial f}{\partial x} \right | _{\substack{x=x_0 \\ y=y_0}}，\left. z_x \right | _{\substack{x=x_0 \\ y=y_0}} \]

方向导数

  • 如果函数的增量与这两点距离的比例存在，则称此为在P点沿着L的方向导数：$ \frac{\partial f}{\partial l} = \lim\limits_{\rho\to0} \frac{f(x+\Delta x, y+\Delta y)-f(x,y)}{\rho} $
  • 如果函数z=f(x,y)在点P(x,y)是可微分的，那么在该点沿任意方向L的方向导数都存在：$ \frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} \cos\varphi + \frac{\partial f}{\partial y} \sin\varphi $。

求函数$ z=xe^{2y} $在点P(1,0)处沿从点P到点Q(2,-1)的方向的方向导数

解：
这里方向 $ \vec{l} $ 即为 $ \vec{PQ}={1,-1}$ ，因此x轴到方向 $ \vec{l} $ 的转角$ \varphi=-\frac \pi4 $

\[\because \quad \left. \frac{\partial z}{\partial x} \right | _{(1,0)}=\left. e^{2y} \right |_{(1,0)} =1; \; \left. \frac{\partial z}{\partial y} \right | _{(1,0)}=\left. 2xe^{2y} \right |_{(1,0)} = 2, \]

所求方向导数：

\[\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} \cos(-\frac \pi4) + \frac{\partial f}{\partial y} \sin(-\frac \pi4)=-\frac {\sqrt{2}}{2} \]

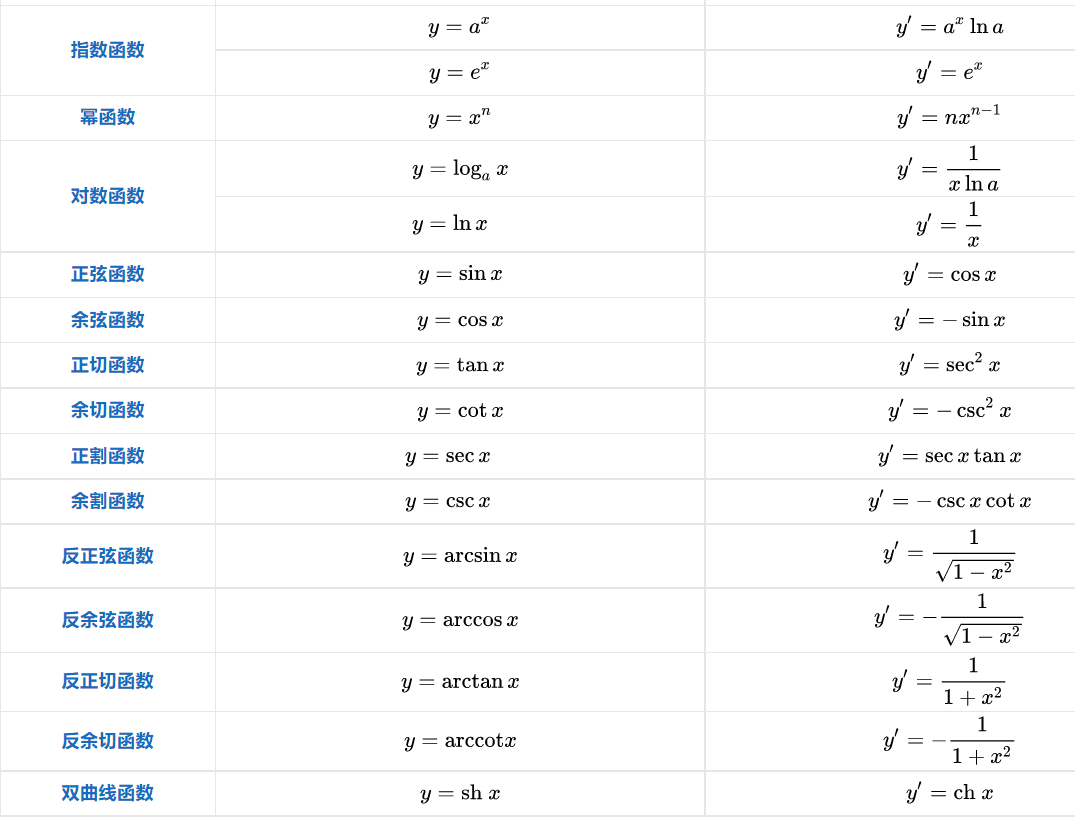
梯度

  • 函数z=f(x,y)在平面域内具有连续的一阶偏导数，对于其中每一个点P(x,y)都有向量

\[ \frac{\partial f}{\partial x}\,\vec{i}+\frac{\partial f}{\partial x}\,\vec{j} , 则称其为函数在点P的梯度： gradf(x,y)= \frac{\partial f}{\partial x}\,\vec{i}+\frac{\partial f}{\partial x}\,\vec{j} \]

  • $ \vec{e}=\cos\varphi\vec{i}+\sin\varphi\vec{j} $ 是方向L上的单位向量

    \[\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} \cos\varphi + \frac{\partial f}{\partial y} \sin\varphi=\{\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\}\cdot\{\cos\varphi, \sin\varphi\} = gradf(x,y)\cdot\vec{e} = |gradf(x,y)|\cos\theta \]

    \[\theta=(gradf(x,y),\vec{e}) ，可见，只有 \cos(gradf(x,y), \vec{e}) =1 时， \frac{\partial f}{\partial l} 才有最大值 \]

​ image-20220222000841210

$ 设u=xyz+z^2+5 , 求grad u $, 并求在点M(0,1,-1)处方向导数的最大(小)值。

解：

\[\because \frac{\partial u}{\partial x} = yz, \frac{\partial u}{\partial y} = xz, \frac{\partial u}{\partial z} = xy+2z, \]

\[\therefore \left. gradu \right |_{(0,1,-1)}=\left. (yz,xz,xy+2z) \right |_{(0,1,-1)} = (-1,0,-2) \]

从而：

\[max\lbrace\frac{\partial u}{\partial x}|_M \rbrace=\lVert gradu \rVert = \sqrt{5} \]

\[min\lbrace\frac{\partial u}{\partial x}|_M \rbrace=\lVert gradu \rVert = -\sqrt{5} \]

微积分

牛顿-莱布尼茨公式

  • 如果F(x)是连续函数f(x)在区间[a,b]上的一个原函数，则：
    $ \int_a^b f(x)dx = F(b)-F(a) $

    有$ f(x)\in C[a,b], 且F^\prime(x)=f(x) $, 则：

    \[\underbrace{\int_a^b f(x)dx=f(\xi)(b-a)}_{积分中值定理}=\underbrace{F^\prime(\xi)(b-a)=F(b)-F(a)}_{微分中值定理} \]

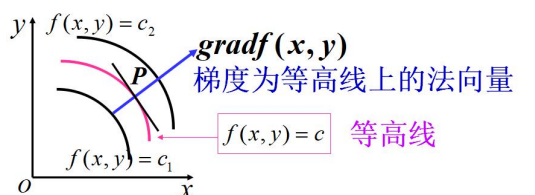
  • 不定积分基本公式（原函数）：
    image-20220222123010208

泰勒多项式与麦克劳林公式

  • \[P_n(x)=f(x_0)+f^\prime(x_0)(x-x_0)+\frac{f^{\prime\prime}(x_0)}{2!}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \]

    称为f(x)在x0关于(x-x0)的n阶泰勒多项式

  • 麦克劳林公式：

    \[f(x)=f(0)+f^\prime(0)x+\frac{f^{\prime\prime}(0)}{2!}(x)^2+\cdots+\frac{f^{(n)}(0)}{n!}(x)^n+\frac{f^{(n+1)(\theta x)}}{(n+1)!}x^{n+1} \; (0<\theta<1) \]

    近似可得：

\[f(x)\approx f(0)+f^\prime(0)x+\frac{f^{\prime\prime}(0)}{2!}(x)^2+\cdots+\frac{f^{(n)}(0)}{n!}(x)^n \]

拉格朗日乘子法

  • 函数z=f(x,y)在条件$ \varphi(x,y)=0 $条件下的极值

    • 构造函数：$ F(x,y)=f(x,y)+\lambda\varphi(x,y) ，其中 \lambda $ 为拉格朗日乘数

      \[\begin{cases} f_x(x,y)+\lambda\varphi_x(x,y)=0 \\ f_y(x,y)+\lambda\varphi_y(x,y)=0 \\ \varphi(x,y)=0 \end{cases} \]

      其中(x,y)就是极值点坐标

  • 多个自变量，函数$ u=f(x,y,z,t) 在条件\varphi(x,y,z,t)=0, \psi(x,y,z,t)=0下的极值 $

    • 构造函数：$ F(x,y,z,t)=f(x,y,z,t)+\lambda_1\varphi(x,y,z,t)+\lambda_2\psi(x,y,z,t) $

      其中$ \lambda_1 , \lambda_2 $为拉格朗日乘数，同样通过偏导为0以及条件求解。

1.函数 $ u=x3y2z $ 在约束条件：x,y,z之和为12，求其最大值

2.在第一卦限内作椭球面 $ \frac{x2}{a2}+\frac{x2}{a2}+\frac{x2}{a2}=1 $
的切平面，使切平面与三个坐标面所转成的四面体体积最小，求切点坐标。

矩阵

  • \[AX=b \quad \begin{cases} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n =b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n =b_1 \\ \cdots\cdots \\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n =b_1 \\ \end{cases} \]

\[A= \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{22} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} ,\quad X= \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{m} \\ \end{pmatrix} ,\quad b= \begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \\ \end{pmatrix} \]

  • 矩阵乘法没有交换律

  • 矩阵转置：行列调换，$ (AT)T=A $

  • 对称矩阵：$ A^T = A $，A即为对称矩阵

  • 逆矩阵：n阶方阵A，如果存在n阶方阵B，使得AB=BA=I（单位阵），则：$ B=A^{-1}$

  • 矩阵的秩：矩阵中最大不相关的向量个数即为矩阵的秩

  • 向量的长度：$ \lVert x \rVert=\sqrt{[x,x]}=\sqrt{x_12+x_22+\cdots+x_n^2}\geq 0 $

  • 向量的正交：两两正交的非零向量组的向量组成为正交向量组。$ a_1\bot a_2 $

特征值与SVD矩阵分解

  • 若σ是线性空间V的线性变换，σ对V中某非零向量x的作用是伸缩：σ（x）=aζ，则称x是σ的属于a的特征向量，a称为σ的特征值。位似变换σk（即对V中所有a，有σk（a）=kα）使V中非零向量均为特征向量，它们同属特征值k；而旋转角θ（0<θ<π）的变换没有特征向量。可以通过矩阵表示求线性变换的特征值、特征向量。

  • 特征值表达了重要程度且和特征向量所对应，那么特征值大的就是主要信息了

  • 奇异值分解( The singular value decomposition )

    一个非方矩阵$ A_{n\times d} $，经过SVD分解后由3个矩阵相乘来表示: $ A_{n\times d} = U_{n\times r}\sum_{r\times n}V_{d\times d}^T $。

    使用另一组正交基$ u_1、u_2表示Mv_1和Mv_2的方向 $

    $σ1 和 σ2分别表示这不同方向向量上的模: Mv_1=\sigma_1u_1 ; Mv_2=\sigma_2u_2 $

    对于向量X在这组基中的表示：$ x=(v_1\cdot x)v_1+(v_2\cdot x)v_2 $ $ (v\cdot x=v^Tx) $

    \[Mx=(v_1\cdot x)Mv_1+(v_2\cdot x)Mv_2 \\ Mx=(v_1\cdot x)\sigma_1u_1+(v_2\cdot x)\sigma_2u_2 \\ Mx=u1\sigma_1v_1^Tx+u_2\sigma_2v_2^Tx \\ M=u_1\sigma_1v_1^T+u_2\sigma_2v_2^T \\ 化简即得：\\ M = U\Sigma V^T \]

随机变量

  • $ f(x_i)=P(X=x_i) $为离散型随机变量的概率函数
  • X为连续随机变量，X在任意区间(a,b]上的概率可以表示为：
    $ P(a<X\leq b) = \int_a^b f(x) dx $
    其中f(x)就叫做X的概率密度函数

极大似然估计

  • 给定联合样本值x关于参数$ \theta 的函数：L(\theta |x)=f(x|\theta) $

    x是随机变量X取得的值，$ \theta $是未知的参数

    $ f(x|\theta)是密度函数，表示给定\theta下的联合密度函数$

    似然函数是关于$ \theta $的函数而密度函数是关于x的函数

  • 极大似然估计：
    离散型样本：$ L(\theta)=\prod_{i=1}^np(x_i;\theta) $

    连续型样本：$ L(\theta)=\prod_{i=1}^nf(x_i;\theta) $

    极大似然估计：$ L(x_1,x_2,\cdots,x_n;\hat\theta)=max_{\theta\in\Theta} L(x_1,x_2,\cdots,x_n;\theta) $

  • 极大似然估计求解：

    • 构造似然函数：$ L(\theta) $
    • 取对数：$ lnL(\theta) $
    • 求偏导：$ \frac{dlnL}{d\theta}=0，得解\theta $

概率论基础

  • 条件概率：$ P(B|A)=\frac{P(AB)}{P(A)} $

  • n重伯努利试验：$ P_n(k)=C_nkpkq^{n-k},, \quad k=0,1,\cdots,n\quad q=1-p $

  • 二维随机变量(X,Y)的分布函数F(x,y)如果存在非负函数f(x,y)有：

    $ F(x,y)=\int_{-\infty}y\int_{-\infty}x{f(u,v)dudv} $

    称f(x,y)为其概率密度

  • 连续型的边缘概率密度：
    对于连续型随机变量(X,Y)，概率密度为f(x,y)。X,Y的边缘概率为：
    $ f_x(x)=\int_{-\infty}^{+\infty}f(x,y)dy \quad f_y(y)=\int_{-\infty}^{+\infty}f(x,y)dx $

    $ F_x(x)=\int_{-\infty}^{+\infty}f_x(t)dt \quad F_y(y)=\int_{-\infty}^{+\infty}f_y(t)dt $

  • 期望
    连续型随机变量X的概率密度为f(x)，若积分$\int_{-\infty}^{+\infty}xf(x)dx $ 绝对收敛，则称积分的值为X的数学期望：

    $ E(X)=\int_{-\infty}^{+\infty}xf(x)dx $

    对于二维连续型随机变量(X,Y)的概率密度z=g(x,y):

    $ E(Z)=E(g(X,Y))=\int_{-\infty}{+\infty}\int_{-\infty}g(x,y)dxdy $

  • 方差
    X为随机变量，如果$ E[X-E(X)]^2 $存在，则称为方差：

    $ D(X)=E[X-E(X)]2=E(X2)-[E(X)]^2 $

  • 马尔科夫不等式：$ P(X\geq a)\leq\frac{E(X)}{a}\quad X\geq0, a>0 $

  • 切比雪夫不等式：

    $ P{|X-E(X)|\geq\epsilon}\leq\frac{\sigma2}{\epsilon2} $

    $ P{|X-E(X)|<\epsilon}\geq 1-\frac{\sigma2}{\epsilon2} $

常用几种分布

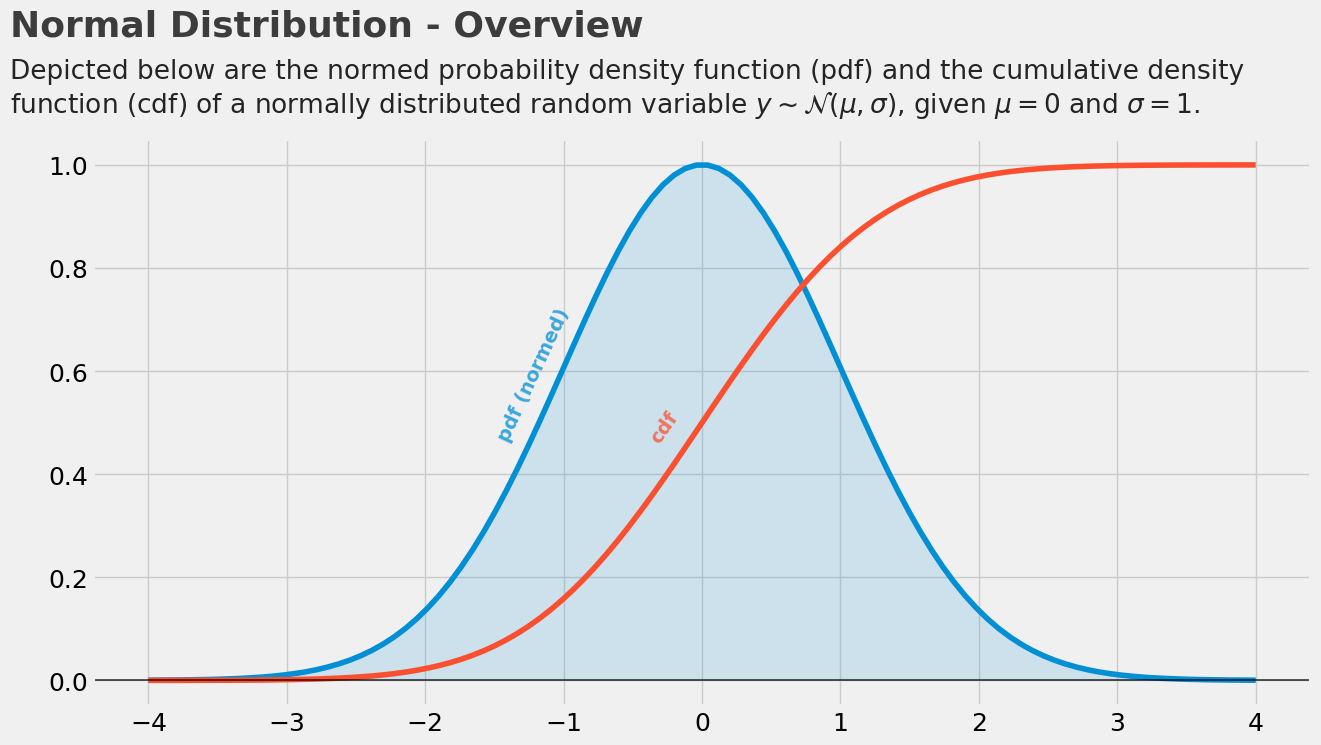
正态分布(Normal Distribution)

若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

\[f(x|\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \quad (\mu是均值 \quad \sigma是标准差) \]

normal_distribution

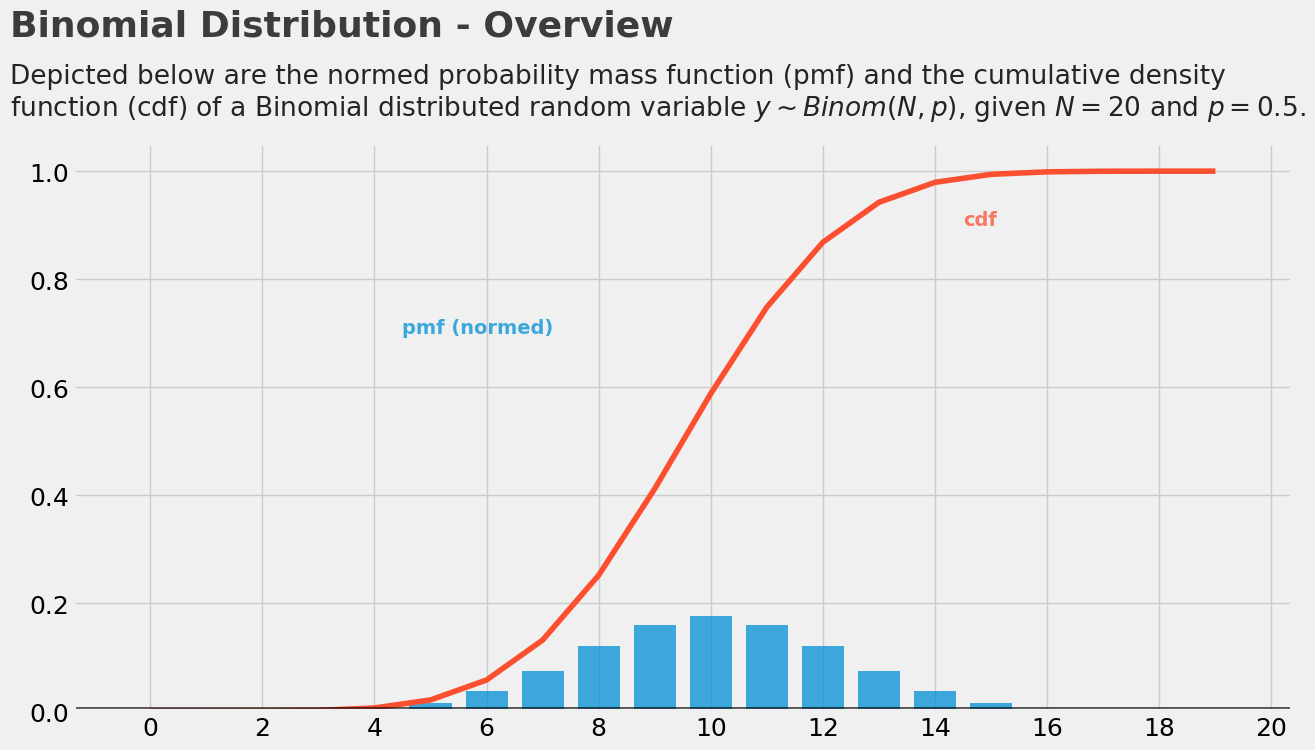
二项式分布(Binomial Distribution)

  • 每个试验都是独立的。

  • 在试验中只有两个可能的结果：成功或失败。

  • 总共进行了n次相同的试验。

  • 所有试验成功和失败的概率是相同的。 （试验是一样的）

\[Binom(k|N,p) = {N \choose k}p^{k}(1-p)^{N-k} \]

\(N \cdot p\) 表示分布的均值

Binomial_Distribution

泊松分布(Poisson Distribution)

  • 任何一个成功的事件都不应该影响另一个成功的事件。

  • 在短时间内成功的概率必须等于在更长的间内成功的概率。

  • 时间间隔很小时，在给间隔时间内成功的概率趋向于零。

泊松分布中使用了这些符号：

  • λ是事件发生的速率

  • t是时间间隔的长

  • X是该时间间隔内的事件数。

  • 其中，X称为泊松随机变量，X的概率分布称为泊松分布。

  • 令μ表示长度为t的间隔中的平均事件数。那么，µ = λ*t。

    \[f(x|\lambda) = \frac{\lambda^{x}e^{-\lambda}}{x!} \]

    where \(\lambda\) denotes the mean of the distribution.

Poisson_Distribution

均匀分布

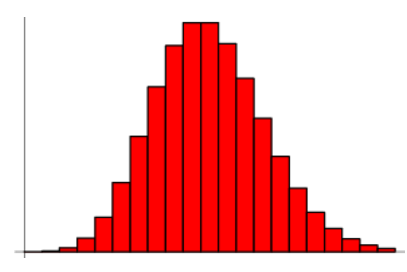
对于投骰子来说，结果是1到6。得到任何一个结果的概率是相等的，这就是均匀分布的基础。与伯努利分布不同，均匀分布的所有可能结果的n个数也是相等的。

7

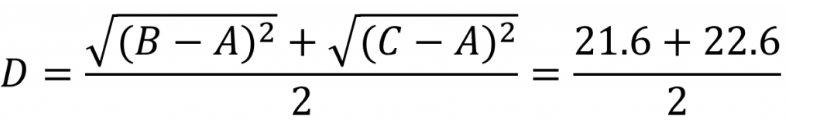
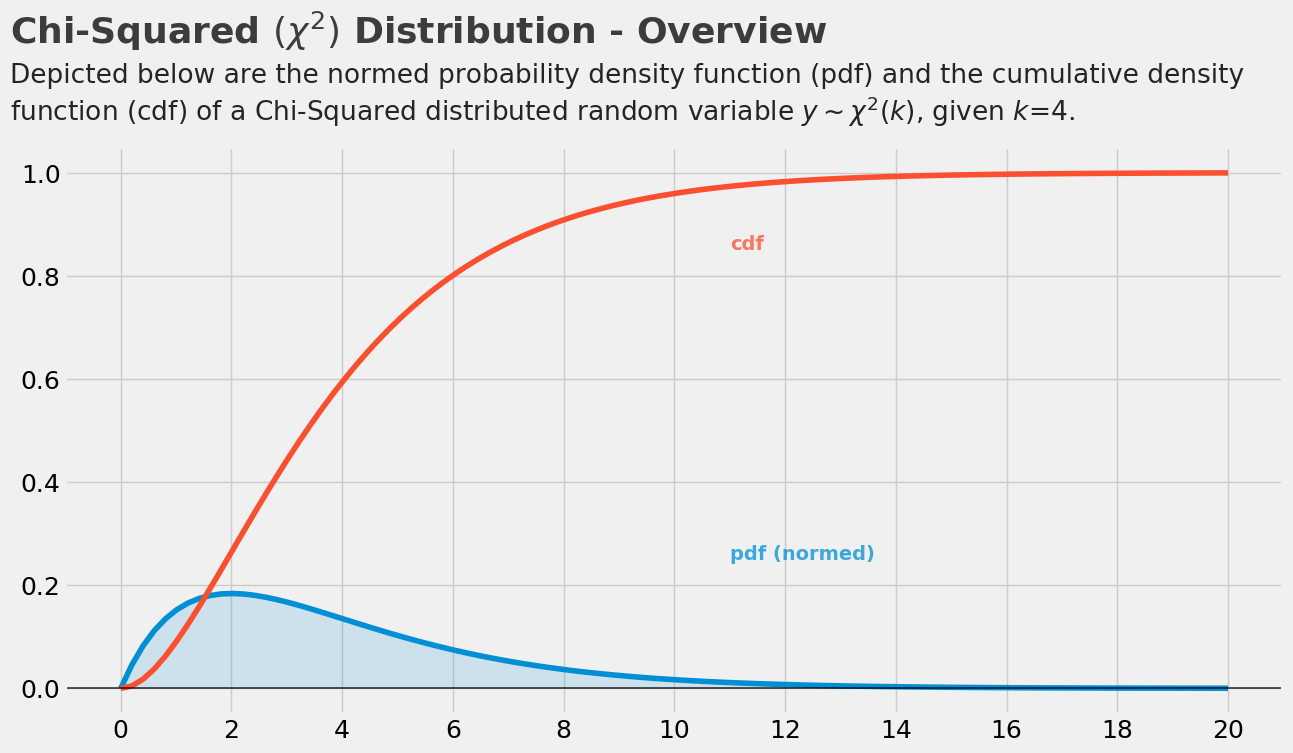
卡方分布（chi-square distribution）

通俗的说就是通过小数量的样本容量去预估总体容量的分布情况

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）

\[\begin{equation} f(x|k) = \begin{cases} \frac{x^{\frac{k}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{k}{2}}\Gamma(\frac{k}{2})}, & \text{if}\ x>0 \\ 0, & \text{otherwise} \end{cases} \end{equation} \]

​ where $ \Gamma(n) = (n-1)! $ and \(k\) denotes the degrees of freedom.

chi-square_distribution

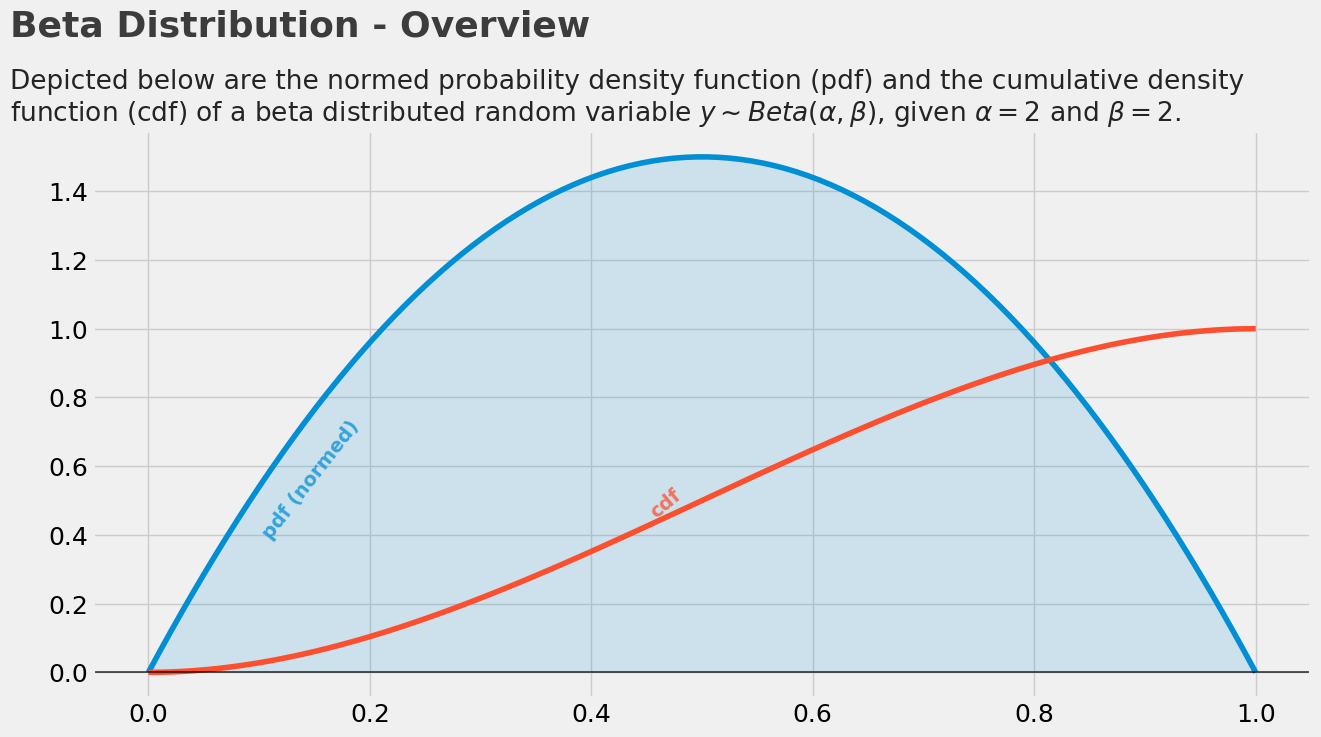
beta分布

beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小

\[Beta(x|\alpha,\beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)} \]

where

\[B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} \]

and

\[\Gamma(n) = (n-1)! \]

\(\alpha\) and \(\beta\) 可以当成是我们成功，失败的次数。

beta_distribution

核函数变换

线性核函数

  • Linear核函数对数据不做任何变换。$ K(x_i,x_j)=x_i^Tx_j $

高斯核函数

  • $ K(X,Y)=exp{-\frac{|X-Y|2}{2\sigma2}} $

熵与激活函数

  • 熵：物体内部的混乱程度。（一件事发生的不确定性）
  • $ H(X)=-\sum_{x\in X}P(x)logP(x) $
  • 常见的激活函数：Sigmoid Tanh Relu 等
    • Sigmoid 函数：是常用的非线性的激活函数, 能够把连续值压缩到0-1区间上。缺点：杀死梯度，非原点中心对称。输出值全为整数会导致梯度全为正或者全为负，优化更新会产生阶梯式情况
    • Tanh函数：原点中心对称，输出在-1到1之间，梯度消失现象依然存在
    • Relu函数：公式简单实用，解决了梯度消失现象，计算速度更快
    • Leaky ReLU：解决了Relu会杀死一部分神经元的情况

描述统计


回归分析


假设检验


相关分析


方差分析


聚类分析


贝叶斯分析与建模


因子分析与降维算法LDA/PCA



  1. 路飞学城 《2周搞定人工智能必备数学基础》 ↩︎

  2. https://scikit-learn.org/stable/ ↩︎

  3. https://www.statsmodels.org/stable/index.html ↩︎

  4. https://docs.scipy.org/doc/scipy-0.19.1/reference/stats.html#module-scipy.stats ↩︎

posted @ 2022-03-08 15:23  9~  阅读(307)  评论(0)  编辑  收藏  举报