1.2.4 动态规划DynamicProgramming
动态规划DynamicProgramming
- 动态规划DynamicProgramming
- 1.0-1 背包问题(0-1 Knapsack Problem)(10)
- 2.最长递增子序列 (LIS)(3)
- 3.最长公共子序列 (LCS)(4)
- 4.找零钱(Coin change)(7)
- 4.Find minimum number of coins that make a given value(45)
- 5.矩阵链乘法(Matrix Chain Multiplication)(8)
- 6.Bellman–Ford Algorithm(29)
- 7.Floyd Warshall Algorithm(16)
- 8.爬楼梯(Count ways to reach the n’th stair)(36)
- 9.切割杆(Cutting a Rod)(13)
- 10.编辑距离(Edit Distance)(5)
- 11.子集和问题(Subset Sum Problem)(32)
- 12.最大和递增子序列(Maximum Sum Increasing Subsequence)(14)
- 13.最大和连续子阵列(Largest Sum Contiguous Subarray)(27)
- 14.最小成本路径(Min Cost Path)(6)
- 15.优化二叉搜索树(Optimal Binary Search Tree)(30)
- 16.划分问题(Partition problem)(18)
- 17.斐波那契数列(Program for Fibonacci numbers)(23)
动态规划是一种算法范式,它通过将给定的复杂问题分解为子问题并存储子问题的结果以避免再次计算相同的结果来解决给定的复杂问题。以下是问题的两个主要属性,表明可以使用动态规划解决给定的问题。
1)重叠子问题
2)最优子结构
1)重叠子问题:
与分而治之,动态规划结合了子问题的解决方案。动态规划主要用于重复需要相同子问题的解决方案时。在动态规划中,子问题的计算解决方案存储在表中,因此不必重新计算这些解决方案。因此,当没有常见(重叠)子问题时,动态规划没有用,因为如果不再需要它们,则存储解决方案没有意义。例如,二分搜索没有常见的子问题。如果我们以斐波那契数列的递归程序为例,就会发现很多子问题需要一次又一次地解决。
# a simple recursive program for Fibonacci numbers
def fib(n):
if n <= 1:
return n
return fib(n - 1) + fib(n - 2)
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
我们可以看到函数 fib(3) 被调用了 2 次。如果我们要存储 fib(3) 的值,那么我们可以重用旧的存储值而不是再次计算它。有以下两种不同的方法来存储这些值,以便可以重复使用这些值:
a)记忆化(自上而下)
b)制表(自下而上)
a) 记忆化(自上而下):问题的记忆化程序类似于递归版本,只是在计算解决方案之前查看查找表进行了小修改。我们初始化一个查找数组,所有初始值都为 NIL。每当我们需要子问题的解决方案时,我们首先查看查找表。如果存在预先计算的值,则返回该值,否则,我们计算该值并将结果放入查找表中,以便稍后重用。
# a program for Memoized version of nth Fibonacci number
# function to calculate nth Fibonacci number
def fib(n, lookup):
# base case
if n <= 1:
lookup[n] = n
# if the value is not calculated previously then calculate it
if lookup[n] is None:
lookup[n] = fib(n-1, lookup) + fib(n-2, lookup)
# return the value corresponding to that value of n
return lookup[n]
# end of function
# Driver program to test the above function
def main():
n = 34
# Declaration of lookup table
# Handles till n = 100
lookup = [None] * 101
print "Fibonacci Number is ", fib(n, lookup)
if __name__ == "__main__":
main()
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
Output
Fibonacci number is 102334155
b) 制表(自下而上):给定问题的制表程序以自下而上的方式构建表格并返回表格中的最后一个条目。例如,对于相同的斐波那契数,我们首先计算 fib(0) 然后 fib(1) 然后 fib(2) 然后 fib(3),依此类推。所以从字面上看,我们正在自下而上地构建子问题的解决方案。
# Python program Tabulated (bottom up) version
def fib(n):
# array declaration
f = [0] * (n + 1)
# base case assignment
f[1] = 1
# calculating the fibonacci and storing the values
for i in xrange(2, n + 1):
f[i] = f[i - 1] + f[i - 2]
return f[n]
# Driver program to test the above function
def main():
n = 9
print "Fibonacci number is ", fib(n)
if __name__ == "__main__":
main()
# This code is contributed by Nikhil Kumar Singh (nickzuck_007)
Output
Fibonacci number is 34
Tabulated 和 Memoized 都存储子问题的解决方案。Memoized 版是按需填表,Tabulated 版是从第一个条目开始,一个个填满。
2)最优子结构:如果给定问题的最优解可以通过使用其子问题的最优解来获得,则给定问题具有最优子结构属性。
例如,最短路径问题具有以下最优子结构性质:
如果节点 x 位于从源节点 u 到目的节点 v 的最短路径中,那么从 u 到 v 的最短路径是从 u 到 x 的最短路径和最短路径的组合从 x 到 v 的路径。标准的 All Pair Shortest Path 算法(如Floyd-Warshall)和单源最短路径算法(如Bellman-Ford)是动态规划的典型示例。
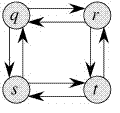
另一方面,最长路径问题没有最优子结构属性。这里的最长路径是指两个节点之间最长的简单路径(没有循环的路径)。考虑以下给出的未加权图。从 q 到 t 有两条最长的路径:q→r→t 和 q→s→t。与最短路径不同,这些最长路径不具有最优子结构属性。例如,最长路径 q→r→t 不是从 q 到 r 的最长路径和从 r 到 t 的最长路径的组合,因为从 q 到 r 的最长路径是 q→s→t→r 和最长路径从r到t是r→q→s→t。
1.0-1 背包问题(0-1 Knapsack Problem)(10)
给定n个物品的重量和价值,将这些物品放入容量为W的背包中,得到背包中的最大总价值。换句话说,给定两个整数数组 val[0..n-1] 和 wt[0..n-1],它们分别代表与 n 个项目相关的值和权重。同样给定一个代表背包容量的整数 W,找出 val[] 的最大值子集,使得该子集的权重之和小于或等于 W。你不能破坏一个项目,要么选择完整的项目,要么不不选择它(0-1 属性)。

方法 1:通过 Brute-Force 算法或穷举搜索递归。
方法:一个简单的解决方案是考虑项目的所有子集,并计算所有子集的总权重和价值。考虑总权重小于 W 的唯一子集。从所有这些子集中选择最大值子集。
最优子结构:要考虑项目的所有子集,每个项目可以有两种情况。
- 情况 1:该项目包含在最优子集中。
- 情况 2:该项目未包含在最优集合中。
因此,可以从'n'个项目中获得的最大值是以下两个值中的最大值。
- n-1 项和 W 权重(不包括第 n 项)得到的最大值。
- 第n个项目的值加上n-1个项目得到的最大值和W减去第n个项目(包括第n个项目)的权重。
如果'nth' 项的权重大于'W',则不能包括第n 项,情况1是唯一的可能性。
# A naive recursive implementation
# of 0-1 Knapsack Problem
# Returns the maximum value that
# can be put in a knapsack of
# capacity W
def knapSack(W, wt, val, n):
# Base Case
if n == 0 or W == 0:
return 0
# If weight of the nth item is
# more than Knapsack of capacity W,
# then this item cannot be included
# in the optimal solution
if (wt[n-1] > W):
return knapSack(W, wt, val, n-1)
# return the maximum of two cases:
# (1) nth item included
# (2) not included
else:
return max(
val[n-1] + knapSack(
W-wt[n-1], wt, val, n-1),
knapSack(W, wt, val, n-1))
# end of function knapSack
#Driver Code
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
print knapSack(W, wt, val, n)
# This code is contributed by Nikhil Kumar Singh
输出
220
需要注意的是,上述函数一次又一次地计算相同的子问题。请参阅以下递归树,K(1, 1) 被评估两次。这个朴素的递归解决方案的时间复杂度是指数级的 (2^n)。
In the following recursion tree, K() refers
to knapSack(). The two parameters indicated in the
following recursion tree are n and W.
The recursion tree is for following sample inputs.
wt[] = {1, 1, 1}, W = 2, val[] = {10, 20, 30}
K(n, W)
K(3, 2)
/ \
/ \
K(2, 2) K(2, 1)
/ \ / \
/ \ / \
K(1, 2) K(1, 1) K(1, 1) K(1, 0)
/ \ / \ / \
/ \ / \ / \
K(0, 2) K(0, 1) K(0, 1) K(0, 0) K(0, 1) K(0, 0)
Recursion tree for Knapsack capacity 2
units and 3 items of 1 unit weight.
复杂度分析:
- 时间复杂度: O(2 n )。
因为有多余的子问题。 - 辅助空间: O(1)。
因为没有使用额外的数据结构来存储值。
由于再次评估子问题,因此该问题具有重叠子问题的属性。
方法2:与其他典型的动态规划(DP)问题一样,通过自底向上构造临时数组K[][]可以避免相同子问题的重新计算。以下是基于动态规划的实现。
方法:在动态编程中,我们将考虑与递归方法中提到的相同的情况。在 DP[][] 表中,让我们考虑从“1”到“W”的所有可能权重作为列,权重可以保留为行。
状态 DP[i][j] 将表示考虑从“1”到“i”的所有值的“j-weight”的最大值。因此,如果我们考虑 'wi'('ith' 行中的权重),我们可以将其填充到所有具有 'weight values > wi' 的列中。现在有两种可能:
- 在给定的列中填写“wi”。
- 不要在给定的列中填写“wi”。
现在我们必须取这两种可能性中的最大值,如果我们不在 'jth' 列中填充 'ith' 权重,那么 DP[i][j] 状态将与 DP[i-1][j] 相同,但是如果我们填充权重,DP[i][j] 将等于 'wi' 的值 + 前一行中权重为 'j-wi' 的列的值。所以我们取这两种可能性中的最大值来填充当前状态。此可视化将使概念清晰:
Let weight elements = {1, 2, 3}
Let weight values = {10, 15, 40}
Capacity=6
0 1 2 3 4 5 6
0 0 0 0 0 0 0 0
1 0 10 10 10 10 10 10
2 0 10 15 25 25 25 25
3 0
Explanation:
For filling 'weight = 2' we come
across 'j = 3' in which
we take maximum of
(10, 15 + DP[1][3-2]) = 25
| |
'2' '2 filled'
not filled
0 1 2 3 4 5 6
0 0 0 0 0 0 0 0
1 0 10 10 10 10 10 10
2 0 10 15 25 25 25 25
3 0 10 15 40 50 55 65
Explanation:
For filling 'weight=3',
we come across 'j=4' in which
we take maximum of (25, 40 + DP[2][4-3])
= 50
For filling 'weight=3'
we come across 'j=5' in which
we take maximum of (25, 40 + DP[2][5-3])
= 55
For filling 'weight=3'
we come across 'j=6' in which
we take maximum of (25, 40 + DP[2][6-3])
= 65
# A Dynamic Programming based Python
# Program for 0-1 Knapsack problem
# Returns the maximum value that can
# be put in a knapsack of capacity W
def knapSack(W, wt, val, n):
K = [[0 for x in range(W + 1)] for x in range(n + 1)]
# Build table K[][] in bottom up manner
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0:
K[i][w] = 0
elif wt[i-1] <= w:
K[i][w] = max(val[i-1]
+ K[i-1][w-wt[i-1]],
K[i-1][w])
else:
K[i][w] = K[i-1][w]
return K[n][W]
# Driver code
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
print(knapSack(W, wt, val, n))
# This code is contributed by Bhavya Jain
输出
220
复杂度分析:
- 时间复杂度: O(N*W)。
其中“N”是权重元素的数量,“W”是容量。对于每个权重元素,我们遍历所有权重容量 1<=w<=W。 - 辅助空间: O(N*W)。
使用大小为“N*W”的二维数组。
改进范围:- 我们使用了相同的方法,但优化了空间复杂度
#include <bits/stdc++.h>
using namespace std;
// we can futher improve the above Knapsack function's space
// complexity
int knapSack(int W, int wt[], int val[], int n)
{
int i, w;
int K[2][W + 1];
// We know we are always using the the current row or
// the previous row of the array/vector . Thereby we can
// improve it further by using a 2D array but with only
// 2 rows i%2 will be giving the index inside the bounds
// of 2d array K
for (i = 0; i <= n; i++) {
for (w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i % 2][w] = 0;
else if (wt[i - 1] <= w)
K[i % 2][w] = max(
val[i - 1]
+ K[(i - 1) % 2][w - wt[i - 1]],
K[(i - 1) % 2][w]);
else
K[i % 2][w] = K[(i - 1) % 2][w];
}
}
return K[n % 2][W];
}
// Driver Code
int main()
{
int val[] = { 60, 100, 120 };
int wt[] = { 10, 20, 30 };
int W = 50;
int n = sizeof(val) / sizeof(val[0]);
cout << knapSack(W, wt, val, n);
return 0;
}
// This code was improved by Udit Singla
复杂度分析:
- 时间复杂度: O(N*W)。
- 辅助空间: O(2*W)
因为我们使用的是二维数组,但只有 2 行。
方法 3:此方法使用记忆技术(递归方法的扩展)。
这种方法基本上是递归方法的扩展,因此我们可以克服计算冗余案例从而增加复杂性的问题。我们可以通过简单地创建一个二维数组来解决这个问题,如果我们第一次得到它,它可以存储一个特定的状态 (n, w)。现在,如果我们再次遇到相同的状态 (n, w) 而不是以指数复杂度计算它,我们可以在恒定时间内直接返回其存储在表中的结果。这种方法在这方面优于递归方法。
# This is the memoization approach of
# 0 / 1 Knapsack in Python in simple
# we can say recursion + memoization = DP
# driver code
val = [60, 100, 120 ]
wt = [10, 20, 30 ]
W = 50
n = len(val)
# We initialize the matrix with -1 at first.
t = [[-1 for i in range(W + 1)] for j in range(n + 1)]
def knapsack(wt, val, W, n):
# base conditions
if n == 0 or W == 0:
return 0
if t[n][W] != -1:
return t[n][W]
# choice diagram code
if wt[n-1] <= W:
t[n][W] = max(
val[n-1] + knapsack(
wt, val, W-wt[n-1], n-1),
knapsack(wt, val, W, n-1))
return t[n][W]
elif wt[n-1] > W:
t[n][W] = knapsack(wt, val, W, n-1)
return t[n][W]
print(knapsack(wt, val, W, n))
# This code is contributed by Prosun Kumar Sarkar
输出
220
复杂度分析:
- 时间复杂度: O(N*W)。
因为避免了状态的冗余计算。 - 辅助空间: O(N*W)。
使用二维数组数据结构存储中间状态-:
方法 4:- 我们再次使用动态规划方法,其空间复杂度更优化。
# code
# A Dynamic Programming based Python
# Program for 0-1 Knapsack problem
# Returns the maximum value that can
# be put in a knapsack of capacity W
def knapSack(W, wt, val, n):
dp = [0 for i in range(W+1)] # Making the dp array
for i in range(1, n+1): # taking first i elements
for w in range(W, 0, -1): # starting from back,so that we also have data of
# previous computation when taking i-1 items
if wt[i-1] <= w:
# finding the maximum value
dp[w] = max(dp[w], dp[w-wt[i-1]]+val[i-1])
return dp[W] # returning the maximum value of knapsack
# Driver code
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
# This code is contributed by Suyash Saxena
print(knapSack(W, wt, val, n))
输出
220
复杂度分析:
时间复杂度:O(N*W)。因为避免了状态的冗余计算。
辅助空间:O(W) 因为我们使用的是一维数组而不是二维数组。
2.最长递增子序列 (LIS)(3)
最长递增子序列 (LIS) 问题是找到给定序列的最长子序列的长度,使子序列的所有元素按递增顺序排序。例如,{10, 22, 9, 33, 21, 50, 41, 60, 80}的LIS长度为6,LIS为{10, 22, 33, 50, 60, 80}。
例:
Input: arr[] = {3, 10, 2, 1, 20}
Output: Length of LIS = 3
The longest increasing subsequence is 3, 10, 20
Input: arr[] = {3, 2}
Output: Length of LIS = 1
The longest increasing subsequences are {3} and {2}
Input: arr[] = {50, 3, 10, 7, 40, 80}
Output: Length of LIS = 4
The longest increasing subsequence is {3, 7, 40, 80}
方法一:递归。
最优子结构:令 arr[0..n-1] 是输入数组,L(i) 是 LIS 的长度,以索引 i 结束,这样 arr[i] 是 LIS 的最后一个元素。
然后,L(i) 可以递归地写为:
L(i) = 1 + max( L(j) ) where 0 < j < i and arr[j] < arr[i]; or
L(i) = 1, if no such j exists.
要找到给定数组的 LIS,我们需要返回 max(L(i)) 其中 0 < i < n。
形式上,以索引 i 结尾的最长递增子序列的长度将比以 i 之前的索引结尾的所有最长递增子序列的最大长度大 1,其中 arr[j] < arr[i] (j < i)。
因此,我们看到 LIS 问题满足最优子结构属性,因为主要问题可以使用子问题的解来解决。
下面给出的递归树将使方法更清晰:
Input : arr[] = {3, 10, 2, 11}
f(i): Denotes LIS of subarray ending at index 'i'
(LIS(1)=1)
f(4) {f(4) = 1 + max(f(1), f(2), f(3))}
/ | \
f(1) f(2) f(3) {f(3) = 1, f(2) and f(1) are > f(3)}
| | \
f(1) f(2) f(1) {f(2) = 1 + max(f(1)}
|
f(1) {f(1) = 1}
# A naive Python implementation of LIS problem
""" To make use of recursive calls, this function must return
two things:
1) Length of LIS ending with element arr[n-1]. We use
max_ending_here for this purpose
2) Overall maximum as the LIS may end with an element
before arr[n-1] max_ref is used this purpose.
The value of LIS of full array of size n is stored in
*max_ref which is our final result """
# global variable to store the maximum
global maximum
def _lis(arr, n):
# to allow the access of global variable
global maximum
# Base Case
if n == 1:
return 1
# maxEndingHere is the length of LIS ending with arr[n-1]
maxEndingHere = 1
"""Recursively get all LIS ending with arr[0], arr[1]..arr[n-2]
IF arr[n-1] is maller than arr[n-1], and max ending with
arr[n-1] needs to be updated, then update it"""
for i in xrange(1, n):
res = _lis(arr, i)
if arr[i-1] < arr[n-1] and res+1 > maxEndingHere:
maxEndingHere = res + 1
# Compare maxEndingHere with overall maximum. And
# update the overall maximum if needed
maximum = max(maximum, maxEndingHere)
return maxEndingHere
def lis(arr):
# to allow the access of global variable
global maximum
# length of arr
n = len(arr)
# maximum variable holds the result
maximum = 1
# The function _lis() stores its result in maximum
_lis(arr, n)
return maximum
# Driver program to test the above function
arr = [10, 22, 9, 33, 21, 50, 41, 60]
n = len(arr)
print "Length of lis is ", lis(arr)
# This code is contributed by NIKHIL KUMAR SINGH
输出
lis 的长度为 5
复杂度分析:
时间复杂度:这种递归方法的时间复杂度是指数级的,因为上面的递归树图中存在重叠子问题的情况。
辅助空间: O(1)。除了内部堆栈空间外,没有用于存储值的外部空间。
方法二:动态规划。
我们可以看到,在上述递归解中,有很多子问题被反复求解。所以这个问题具有重叠子结构的性质,并且可以通过使用 Memoization 或 Tabulation 来避免相同子问题的重新计算。
方法的模拟将使事情变得清楚:
Input : arr[] = {3, 10, 2, 11}
LIS[] = {1, 1, 1, 1} (initially)
迭代模拟:
- arr[2] > arr[1]
- arr[3] < arr[1]
- arr[3] < arr[2]
- arr[4] > arr[1]
- arr[4] > arr[2]
- arr[4] > arr[3]
我们可以通过使用制表来避免重新计算子问题,如下面的代码所示:
# Dynamic programming Python implementation
# of LIS problem
# lis returns length of the longest
# increasing subsequence in arr of size n
def lis(arr):
n = len(arr)
# Declare the list (array) for LIS and
# initialize LIS values for all indexes
lis = [1]*n
# Compute optimized LIS values in bottom up manner
for i in range(1, n):
for j in range(0, i):
if arr[i] > arr[j] and lis[i] < lis[j] + 1:
lis[i] = lis[j]+1
# Initialize maximum to 0 to get
# the maximum of all LIS
maximum = 0
# Pick maximum of all LIS values
for i in range(n):
maximum = max(maximum, lis[i])
return maximum
# end of lis function
# Driver program to test above function
arr = [10, 22, 9, 33, 21, 50, 41, 60]
print "Length of lis is", lis(arr)
# This code is contributed by Nikhil Kumar Singh
输出
lis 的长度为 5
复杂度分析:
- 时间复杂度: O(n 2 )。
由于使用了嵌套循环。 - 辅助空间: O(n)。
使用任何数组在每个索引处存储 LIS 值。
注意:上述动态规划 (DP) 解决方案的时间复杂度为 O(n^2),而 LIS 问题有一个 O(N log N) 解决方案。我们没有在这里讨论 O(N log N) 解决方案,因为这篇文章的目的是用一个简单的例子来解释动态规划。请参阅下面的帖子以了解 O(N log N) 解决方案。
最长递增子序列大小 (N log N)
方法 3:动态规划
如果我们仔细观察这个问题,那么我们可以将这个问题转换为最长公共子序列问题。首先,我们将创建另一个原始数组的唯一元素数组并对其进行排序。现在,我们数组的最长递增子序列必须作为排序数组中的一个子序列存在。这就是为什么我们的问题现在简化为找到两个数组之间的公共子序列。
Eg. arr =[50,3,10,7,40,80]
// Sorted array
arr1 = [3,7,10,40,50,80]
// LIS is longest common subsequence between the two arrays
ans = 4
The longest increasing subsequence is {3, 7, 40, 80}
# Dynamic Programming Approach of Finding LIS by reducing the problem to longest common Subsequence
def lis(a):
n = len(a)
# Creating the sorted list
b = sorted(list(set(a)))
m = len(b)
# Creating dp table for storing the answers of sub problems
dp = [[-1 for i in range(m+1)] for j in range(n+1)]
# Finding Longest common Subsequence of the two arrays
for i in range(n+1):
for j in range(m+1):
if i == 0 or j == 0:
dp[i][j] = 0
elif a[i-1] == b[j-1]:
dp[i][j] = 1+dp[i-1][j-1]
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
# Driver program to test above function
arr = [10, 22, 9, 33, 21, 50, 41, 60]
print("Length of lis is ", lis(arr))
# This code is Contributed by Dheeraj Khatri
输出
lis 的长度为 5
复杂度分析:O(n*n) 由于使用了嵌套循环
空间复杂度:O(n*n) 因为矩阵用于存储值。
3.最长公共子序列 (LCS)(4)
最长公共子序列 (LCS) 问题,作为可以使用动态规划解决的另一个示例问题。
LCS 问题陈述:给定两个序列,找出它们中存在的最长子序列的长度。子序列是以相同的相对顺序出现的序列,但不一定是连续的。例如,“abc”、“abg”、“bdf”、“aeg”、'”acefg”等都是“abcdefg”的子序列。
示例:
输入序列“ABCDGH”和“AEDFHR”的
LCS是长度为 3 的“ADH”。 输入序列“AGGTAB”和“GXTXAYB”的 LCS 是长度为 4 的“GTAB”。
这个问题的天真解决方案是生成两个给定序列的所有子序列并找到最长的匹配子序列。该解决方案在时间复杂度方面呈指数级增长。让我们看看这个问题如何拥有动态规划 (DP) 问题的两个重要属性。
1) 最优子结构:
让输入序列分别为长度为 m 和 n 的 X[0..m-1] 和 Y[0..n-1]。并令 L(X[0..m-1], Y[0..n-1]) 为两个序列 X 和 Y 的 LCS 长度。以下是 L(X[0..n-1]) 的递归定义。 m-1], Y[0..n-1])。
如果两个序列的最后一个字符匹配(或 X[m-1] == Y[n-1]),则
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])
如果两个序列的最后一个字符不匹配(或 X[m-1] != Y[n-1]),则
L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2]) )
示例:
1) 考虑输入字符串“AGGTAB”和“GXTXAYB”。字符串的最后一个字符匹配。所以LCS的长度可以写成:
L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”)
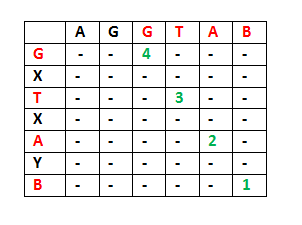
2) 考虑输入字符串“ABCDGH”和“AEDFHR”。字符串的最后一个字符不匹配。所以LCS的长度可以写成:
L(“ABCDGH”, “AEDFHR”) = MAX ( L(“ABCDG”, “AEDFH R ”), L(“ABCDG H ”, “AEDFH”) )
所以LCS问题具有最优子结构性质,因为主要问题可以使用子问题的解来解决。
2) 重叠子问题:
以下是 LCS 问题的简单递归实现。实现只是遵循上面提到的递归结构。
# A Naive recursive Python implementation of LCS problem
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0;
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1);
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
# Driver program to test the above function
X = "AGGTAB"
Y = "GXTXAYB"
print "Length of LCS is ", lcs(X , Y, len(X), len(Y))
Output:
Length of LCS is 4
上述朴素递归方法的时间复杂度在最坏情况下为 O(2^n),最坏情况发生在 X 和 Y 的所有字符不匹配时,即 LCS 的长度为 0。
考虑到上述实现,以下是输入字符串“AXYT”和“AYZX”的部分递归树
lcs("AXYT", "AYZX")
/
lcs("AXY", "AYZX") lcs("AXYT", "AYZ")
/ /
lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")
在上面的部分递归树中,lcs(“AXY”, “AYZ”) 被求解了两次。如果我们画出完整的递归树,那么我们可以看到有很多子问题被一次又一次地解决了。所以这个问题具有重叠子结构的性质,并且可以通过使用 Memoization 或 Tabulation 来避免相同子问题的重新计算。以下是 LCS 问题的列表实现。
# Dynamic Programming implementation of LCS problem
def lcs(X , Y):
# find the length of the strings
m = len(X)
n = len(Y)
# declaring the array for storing the dp values
L = [[None]*(n+1) for i in xrange(m+1)]
"""Following steps build L[m+1][n+1] in bottom up fashion
Note: L[i][j] contains length of LCS of X[0..i-1]
and Y[0..j-1]"""
for i in range(m+1):
for j in range(n+1):
if i == 0 or j == 0 :
L[i][j] = 0
elif X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1]+1
else:
L[i][j] = max(L[i-1][j] , L[i][j-1])
# L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1]
return L[m][n]
#end of function lcs
# Driver program to test the above function
X = "AGGTAB"
Y = "GXTXAYB"
print "Length of LCS is ", lcs(X, Y)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
输出:
LCS的长度为4
上述实现的时间复杂度为 O(mn),这比 Naive Recursive 实现的最坏情况时间复杂度要好得多。
4.找零钱(Coin change)(7)
给定一个价值 N,如果我们想用 N 美分找零,并且我们有无限供应每个 S = { S1, S2, .. , Sm} 价值的硬币,我们有多少种方法可以找零?硬币的顺序无关紧要。
例如,对于 N = 4 和 S = {1,2,3},有四种解:{1,1,1,1},{1,1,2},{2,2},{1, 3}。所以输出应该是 4。对于 N = 10 和 S = {2, 5, 3, 6},有五种解:{2,2,2,2,2}, {2,2,3,3}, {2,2,6}、{2,3,5} 和 {5,5}。所以输出应该是5。
1) 最优子结构
为了计算解的总数,我们可以将所有集合解分成两个集合。
1) 不包含第 m 个硬币(或 Sm)的解决方案。
2) 包含至少一个 Sm 的解决方案。
设 count(S[], m, n) 为计算解个数的函数,则可写为 count(S[], m-1, n) 和 count(S[], m, n-Sm)。
因此,该问题具有最优子结构性质,因为该问题可以使用子问题的解来解决。
2) 重叠子问题
以下是硬币找零问题的简单递归实现。实现只是遵循上面提到的递归结构。
3)方法(算法)
这里给定面额的每个硬币都可以无限次出现。(允许重复),这就是我们所说的UNBOUNDED KNAPSACK。对于特定面额的硬币,我们有 2 种选择,i) 包含或 ii) 排除。但在这里,包容过程不仅仅是一次;我们可以将任何面额包含任意次数,直到 N<0。
基本上,如果我们在 s[m-1] 处,我们可以采用该硬币的多个实例(无限包含),即count(S, m, n – S[m-1] );然后我们移动到 s[m-2]。移动到 s[m-2] 后,我们无法向后移动,也无法为 s[m-1] 做出选择,即count(S, m-1, n )。
最后,由于我们必须找到方法的总数,因此我们将添加这两种可能的选择,即count(S, m, n – S[m-1] ) + count(S, m-1, n ) ;这将是我们需要的答案。
# Recursive Python3 program for
# coin change problem.
# Returns the count of ways we can sum
# S[0...m-1] coins to get sum n
def count(S, m, n ):
# If n is 0 then there is 1
# solution (do not include any coin)
if (n == 0):
return 1
# If n is less than 0 then no
# solution exists
if (n < 0):
return 0;
# If there are no coins and n
# is greater than 0, then no
# solution exist
if (m <=0 and n >= 1):
return 0
# count is sum of solutions (i)
# including S[m-1] (ii) excluding S[m-1]
return count( S, m - 1, n ) + count( S, m, n-S[m-1] );
# Driver program to test above function
arr = [1, 2, 3]
m = len(arr)
print(count(arr, m, 4))
# This code is contributed by Smitha Dinesh Semwal
输出
4
需要注意的是,上述函数一次又一次地计算相同的子问题。对于 S = {1, 2, 3} 和 n = 5,请参见以下递归树。
函数 C({1}, 3) 被调用了两次。如果我们绘制完整的树,那么我们可以看到有许多子问题被多次调用。
C() --> count()
C({1,2,3}, 5)
/ \
/ \
C({1,2,3}, 2) C({1,2}, 5)
/ \ / \
/ \ / \
C({1,2,3}, -1) C({1,2}, 2) C({1,2}, 3) C({1}, 5)
/ \ / \ / \
/ \ / \ / \
C({1,2},0) C({1},2) C({1,2},1) C({1},3) C({1}, 4) C({}, 5)
/ \ / \ /\ / \
/ \ / \ / \ / \
. . . . . . C({1}, 3) C({}, 4)
/ \
/ \
. .
由于再次调用相同的子问题,该问题具有重叠子问题的性质。因此,硬币找零问题具有动态规划问题的两个性质。与其他典型的动态规划 (DP) 问题一样,通过以自下而上的方式构造临时数组 table[][] 可以避免相同子问题的重新计算。
# Dynamic Programming Python implementation of Coin
# Change problem
def count(S, m, n):
# We need n+1 rows as the table is constructed
# in bottom up manner using the base case 0 value
# case (n = 0)
table = [[0 for x in range(m)] for x in range(n+1)]
# Fill the entries for 0 value case (n = 0)
for i in range(m):
table[0][i] = 1
# Fill rest of the table entries in bottom up manner
for i in range(1, n+1):
for j in range(m):
# Count of solutions including S[j]
x = table[i - S[j]][j] if i-S[j] >= 0 else 0
# Count of solutions excluding S[j]
y = table[i][j-1] if j >= 1 else 0
# total count
table[i][j] = x + y
return table[n][m-1]
# Driver program to test above function
arr = [1, 2, 3]
m = len(arr)
n = 4
print(count(arr, m, n))
# This code is contributed by Bhavya Jain
输出
4
时间复杂度: O(mn)
以下是方法2的简化版,这里需要的辅助空间仅为O(n)。
# Dynamic Programming Python implementation of Coin
# Change problem
def count(S, m, n):
# table[i] will be storing the number of solutions for
# value i. We need n+1 rows as the table is constructed
# in bottom up manner using the base case (n = 0)
# Initialize all table values as 0
table = [0 for k in range(n+1)]
# Base case (If given value is 0)
table[0] = 1
# Pick all coins one by one and update the table[] values
# after the index greater than or equal to the value of the
# picked coin
for i in range(0,m):
for j in range(S[i],n+1):
table[j] += table[j-S[i]]
return table[n]
# Driver program to test above function
arr = [1, 2, 3]
m = len(arr)
n = 4
x = count(arr, m, n)
print (x)
# This code is contributed by Afzal Ansari
4.Find minimum number of coins that make a given value(45)
给定值 V,如果我们想改变 V 美分,并且我们有无限供应 C = { C1, C2, .., Cm} 价值的硬币中的每一个,那么最少的硬币数量是多少?改变?如果无法进行更改,则打印 -1。
Input: coins[] = {25, 10, 5}, V = 30
Output: Minimum 2 coins required
We can use one coin of 25 cents and one of 5 cents
Input: coins[] = {9, 6, 5, 1}, V = 11
Output: Minimum 2 coins required
We can use one coin of 6 cents and 1 coin of 5 cents
这个问题是讨论的找零钱问题的变体。在这里,我们需要找到具有最少硬币数量的解决方案,而不是找到可能解决方案的总数。
可以使用以下递归公式计算值 V 的最小硬币数量。
If V == 0, then 0 coins required.
If V > 0
minCoins(coins[0..m-1], V) = min {1 + minCoins(V-coin[i])}
where i varies from 0 to m-1
and coin[i] <= V
下面是基于上述递归公式的递归解决方案。
# A Naive recursive python program to find minimum of coins
# to make a given change V
import sys
# m is size of coins array (number of different coins)
def minCoins(coins, m, V):
# base case
if (V == 0):
return 0
# Initialize result
res = sys.maxsize
# Try every coin that has smaller value than V
for i in range(0, m):
if (coins[i] <= V):
sub_res = minCoins(coins, m, V-coins[i])
# Check for INT_MAX to avoid overflow and see if
# result can minimized
if (sub_res != sys.maxsize and sub_res + 1 < res):
res = sub_res + 1
return res
# Driver program to test above function
coins = [9, 6, 5, 1]
m = len(coins)
V = 11
print("Minimum coins required is",minCoins(coins, m, V))
# This code is contributed by
# Smitha Dinesh Semwal
输出:
所需的最少硬币为 2
上述解决方案的时间复杂度是指数级的。如果我们画出完整的递归树,我们可以观察到很多子问题被一次又一次地解决了。例如,当我们从 V = 11 开始时,我们可以通过减 5 次和减 5 次来达到 6。所以 6 的子问题被调用了两次。
由于再次调用相同的子问题,此问题具有重叠子问题的属性。因此,最小硬币问题具有动态规划问题的两个性质。与其他典型的动态规划 (DP) 问题一样,可以通过以自底向上的方式构造临时数组 table 来避免对相同子问题的重新计算。以下是基于动态规划的解决方案。
# A Dynamic Programming based Python3 program to
# find minimum of coins to make a given change V
import sys
# m is size of coins array (number of
# different coins)
def minCoins(coins, m, V):
# table[i] will be storing the minimum
# number of coins required for i value.
# So table[V] will have result
table = [0 for i in range(V + 1)]
# Base case (If given value V is 0)
table[0] = 0
# Initialize all table values as Infinite
for i in range(1, V + 1):
table[i] = sys.maxsize
# Compute minimum coins required
# for all values from 1 to V
for i in range(1, V + 1):
# Go through all coins smaller than i
for j in range(m):
if (coins[j] <= i):
sub_res = table[i - coins[j]]
if (sub_res != sys.maxsize and
sub_res + 1 < table[i]):
table[i] = sub_res + 1
if table[V] == sys.maxsize:
return -1
return table[V]
# Driver Code
if __name__ == "__main__":
coins = [9, 6, 5, 1]
m = len(coins)
V = 11
print("Minimum coins required is ",
minCoins(coins, m, V))
# This code is contributed by ita_c
输出:
所需的最少硬币为 2
上述解的时间复杂度为O(mV)。
5.矩阵链乘法(Matrix Chain Multiplication)(8)
给定一个矩阵序列,找到将这些矩阵相乘的最有效方法。问题实际上不是执行乘法,而只是决定执行乘法的顺序。
我们有很多选择来乘以矩阵链,因为矩阵乘法是关联的。换句话说,无论我们如何将乘积括起来,结果都是一样的。例如,如果我们有四个矩阵 A、B、C 和 D,我们将有:
(ABC)D = (AB)(CD) = A(BCD) = ....
但是,我们将乘积括起来的顺序会影响计算乘积所需的简单算术运算的数量或效率。例如,假设 A 是一个 10 × 30 的矩阵,B 是一个 30 × 5 的矩阵,而 C 是一个 5 × 60 的矩阵。然后,
(AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 次操作
A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 次操作。
显然,第一个括号需要较少的操作次数。
给定一个数组 p[],它表示矩阵链,使得第 i 个矩阵 Ai 的维度为 p[i-1] xp[i]。我们需要编写一个函数 MatrixChainOrder(),它应该返回乘法链所需的最小乘法次数。
Input: p[] = {40, 20, 30, 10, 30}
Output: 26000
There are 4 matrices of dimensions 40x20, 20x30, 30x10 and 10x30.
Let the input 4 matrices be A, B, C and D. The minimum number of
multiplications are obtained by putting parenthesis in following way
(A(BC))D --> 20*30*10 + 40*20*10 + 40*10*30
Input: p[] = {10, 20, 30, 40, 30}
Output: 30000
There are 4 matrices of dimensions 10x20, 20x30, 30x40 and 40x30.
Let the input 4 matrices be A, B, C and D. The minimum number of
multiplications are obtained by putting parenthesis in following way
((AB)C)D --> 10*20*30 + 10*30*40 + 10*40*30
Input: p[] = {10, 20, 30}
Output: 6000
There are only two matrices of dimensions 10x20 and 20x30. So there
is only one way to multiply the matrices, cost of which is 10*20*30
1)最优子结构:
一个简单的解决方案是在所有可能的位置放置括号,计算每个放置的成本并返回最小值。在大小为 n 的矩阵链中,我们可以以 n-1 种方式放置第一组括号。例如,如果给定的链是 4 个矩阵。设链为ABCD,则第一组括号外侧有3种方式:(A)(BCD)、(AB)(CD)和(ABC)(D)。因此,当我们放置一组括号时,我们将问题划分为更小的子问题。因此,该问题具有最优子结构性质,可以使用递归轻松解决。
将大小为 n 的链相乘所需的最小乘法次数 = 所有 n-1 个放置的最小值(这些放置创建更小的子问题)
2) Overlapping Subproblems
以下是简单地遵循上述最优子结构属性的递归实现。
# A naive recursive implementation that
# simply follows the above optimal
# substructure property
import sys
# Matrix A[i] has dimension p[i-1] x p[i]
# for i = 1..n
def MatrixChainOrder(p, i, j):
if i == j:
return 0
_min = sys.maxsize
# place parenthesis at different places
# between first and last matrix,
# recursively calculate count of
# multiplications for each parenthesis
# placement and return the minimum count
for k in range(i, j):
count = (MatrixChainOrder(p, i, k)
+ MatrixChainOrder(p, k + 1, j)
+ p[i-1] * p[k] * p[j])
if count < _min:
_min = count
# Return minimum count
return _min
# Driver code
arr = [1, 2, 3, 4, 3]
n = len(arr)
print("Minimum number of multiplications is ",
MatrixChainOrder(arr, 1, n-1))
# This code is contributed by Aryan Garg
输出
最小乘法次数为 30
上述朴素递归方法的时间复杂度是指数级的。需要注意的是,上述函数一次又一次地计算相同的子问题。对于大小为 4 的矩阵链,请参见以下递归树。函数 MatrixChainOrder(p, 3, 4) 被调用两次。我们可以看到有很多子问题被多次调用。

由于再次调用相同的子问题,该问题具有重叠子问题的性质。因此,矩阵链乘法问题具有动态规划问题的两个属性。与其他典型的动态规划 (DP) 问题一样,通过以自下而上的方式构造临时数组 m 可以避免相同子问题的重新计算。
动态规划解决方案
以下是使用动态规划(制表与记忆)的矩阵链乘法问题的实现
使用记忆——
# Python program using memoization
import sys
dp = [[-1 for i in range(100)] for j in range(100)]
# Function for matrix chain multiplication
def matrixChainMemoised(p, i, j):
if(i == j):
return 0
if(dp[i][j] != -1):
return dp[i][j]
dp[i][j] = sys.maxsize
for k in range(i,j):
dp[i][j] = min(dp[i][j], matrixChainMemoised(p, i, k) + matrixChainMemoised(p, k + 1, j)+ p[i - 1] * p[k] * p[j])
return dp[i][j]
def MatrixChainOrder(p,n):
i = 1
j = n - 1
return matrixChainMemoised(p, i, j)
# Driver Code
arr = [1, 2, 3, 4]
n = len(arr)
print("Minimum number of multiplications is",MatrixChainOrder(arr, n))
# This code is contributed by rag2127
输出
最小乘法次数为 18
使用制表 --
# Dynamic Programming Python implementation of Matrix
# Chain Multiplication. See the Cormen book for details
# of the following algorithm
import sys
# Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
def MatrixChainOrder(p, n):
# For simplicity of the program,
# one extra row and one
# extra column are allocated in m[][].
# 0th row and 0th
# column of m[][] are not used
m = [[0 for x in range(n)] for x in range(n)]
# m[i, j] = Minimum number of scalar
# multiplications needed
# to compute the matrix A[i]A[i + 1]...A[j] =
# A[i..j] where
# dimension of A[i] is p[i-1] x p[i]
# cost is zero when multiplying one matrix.
for i in range(1, n):
m[i][i] = 0
# L is chain length.
for L in range(2, n):
for i in range(1, n-L + 1):
j = i + L-1
m[i][j] = sys.maxint
for k in range(i, j):
# q = cost / scalar multiplications
q = m[i][k] + m[k + 1][j] + p[i-1]*p[k]*p[j]
if q < m[i][j]:
m[i][j] = q
return m[1][n-1]
# Driver code
arr = [1, 2, 3, 4]
size = len(arr)
print("Minimum number of multiplications is " +
str(MatrixChainOrder(arr, size)))
# This Code is contributed by Bhavya Jain
输出
最小乘法次数为 18
时间复杂度: O(n 3 )
辅助空间: O(n 2 )
6.Bellman–Ford Algorithm(29)
给定一个图和图中的源顶点src,找到从src到给定图中所有顶点的最短路径。该图可能包含负权重边。
我们已经讨论了针对这个问题的Dijkstra 算法。Dijkstra 算法是一种贪心算法,时间复杂度为 O((V+E)LogV)(使用斐波那契堆)。Dijkstra 不适用于负权重循环图,Bellman-Ford 适用于此类图。Bellman-Ford 也比 Dijkstra 更简单,并且非常适合分布式系统。但是 Bellman-Ford 的时间复杂度是 O(VE),比 Dijkstra 还多。
算法
以下是详细步骤。
输入:图形和源顶点src
输出:从src到所有顶点的最短距离。如果存在负重量周期,则不计算最短距离,报告负重量周期。
1)这一步将源到所有顶点的距离初始化为无穷大,到源本身的距离初始化为 0。创建一个大小为 |V| 的数组 dist[] 除了 dist[src] 其中 src 是源顶点之外,所有值都为无穷大。
2)这一步计算最短距离。跟随 |V|-1 次,其中 |V| 是给定图中的顶点数。
..... a)对每个边 uv 执行以下操作
………………如果dist[v] > dist[u] + 边uv 的权重,则更新dist[v]
………………….dist[v] = dist[u] + 边uv 的权重
3)此步骤报告图中是否存在负权重循环。对每条边 uv 进行以下操作
……如果 dist[v] > dist[u] + 边 uv 的权重,则“图包含负权重循环”
步骤 3 的想法是,如果图不存在,则步骤 2 保证最短距离' t 包含负权重循环。如果我们再一次遍历所有边并为任何顶点获得一条更短的路径,那么就会出现负权重循环 这是
如何工作的?与其他动态规划问题一样,该算法以自底向上的方式计算最短路径。它首先计算路径中最多有一条边的最短距离。然后,它计算最多有 2 条边的最短路径,依此类推。在外循环的第 i 次迭代之后,计算最多具有 i 条边的最短路径。可以有最大值 |V| – 任何简单路径中的 1 个边,这就是外循环运行 |v| 的原因 – 1 次。这个想法是,假设没有负权重循环,如果我们计算了最多有 i 条边的最短路径,那么对所有边的迭代保证给出最多有 (i+1) 条边的最短路径。
示例
让我们通过以下示例图来理解算法。
让给定的源顶点为 0。将所有距离初始化为无穷大,除了到源本身的距离。图中的顶点总数为 5,因此所有边都必须处理 4 次。

让所有边按以下顺序处理:(B, E), (D, B), (B, D), (A, B), (A, C), (D, C), (B, C) ), (E, D)。第一次处理所有边时,我们得到以下距离。第一行显示初始距离。第二行显示处理边 (B, E)、(D, B)、(B, D) 和 (A, B) 时的距离。第三行显示处理 (A, C) 时的距离。第四行显示何时处理(D,C),(B,C)和(E,D)。

第一次迭代保证给出最多 1 条边长的所有最短路径。当第二次处理所有边时,我们得到以下距离(最后一行显示最终值)。

第二次迭代保证给出最多 2 条边长的所有最短路径。该算法将所有边再处理 2 次。第二次迭代后距离最小化,因此第三次和第四次迭代不会更新距离。
执行:
# Python3 program for Bellman-Ford's single source
# shortest path algorithm.
# Class to represent a graph
class Graph:
def __init__(self, vertices):
self.V = vertices # No. of vertices
self.graph = []
# function to add an edge to graph
def addEdge(self, u, v, w):
self.graph.append([u, v, w])
# utility function used to print the solution
def printArr(self, dist):
print("Vertex Distance from Source")
for i in range(self.V):
print("{0}\t\t{1}".format(i, dist[i]))
# The main function that finds shortest distances from src to
# all other vertices using Bellman-Ford algorithm. The function
# also detects negative weight cycle
def BellmanFord(self, src):
# Step 1: Initialize distances from src to all other vertices
# as INFINITE
dist = [float("Inf")] * self.V
dist[src] = 0
# Step 2: Relax all edges |V| - 1 times. A simple shortest
# path from src to any other vertex can have at-most |V| - 1
# edges
for _ in range(self.V - 1):
# Update dist value and parent index of the adjacent vertices of
# the picked vertex. Consider only those vertices which are still in
# queue
for u, v, w in self.graph:
if dist[u] != float("Inf") and dist[u] + w < dist[v]:
dist[v] = dist[u] + w
# Step 3: check for negative-weight cycles. The above step
# guarantees shortest distances if graph doesn't contain
# negative weight cycle. If we get a shorter path, then there
# is a cycle.
for u, v, w in self.graph:
if dist[u] != float("Inf") and dist[u] + w < dist[v]:
print("Graph contains negative weight cycle")
return
# print all distance
self.printArr(dist)
g = Graph(5)
g.addEdge(0, 1, -1)
g.addEdge(0, 2, 4)
g.addEdge(1, 2, 3)
g.addEdge(1, 3, 2)
g.addEdge(1, 4, 2)
g.addEdge(3, 2, 5)
g.addEdge(3, 1, 1)
g.addEdge(4, 3, -3)
# Print the solution
g.BellmanFord(0)
# Initially, Contributed by Neelam Yadav
# Later On, Edited by Himanshu Garg
输出:
与源的顶点距离
0 0
1 -1
2 2
3 -2
4 1
注释
1)在各种图形应用中都可以找到负权重。例如,如果我们沿着这条路径走,我们可能会获得一些优势,而不是为一条路径付出代价。
2) Bellman-Ford 在分布式系统上工作得更好(比 Dijkstra 更好)。与 Dijkstra 需要找到所有顶点的最小值不同,在 Bellman-Ford 中,边被一条一条地考虑。
3) Bellman-Ford 不适用于带负边的无向图,因为它会声明为负循环。
7.Floyd Warshall Algorithm(16)
在弗洛伊德Warshall算法是解决所有配对最短路径问题。问题是在给定的边加权有向图中找到每对顶点之间的最短距离。
Example:
Input:
graph[][] = { {0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0} }
which represents the following graph
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3
Note that the value of graph[i][j] is 0 if i is equal to j
And graph[i][j] is INF (infinite) if there is no edge from vertex i to j.
Output:
Shortest distance matrix
0 5 8 9
INF 0 3 4
INF INF 0 1
INF INF INF 0
Floyd Warshall 算法
作为第一步,我们初始化与输入图矩阵相同的解矩阵。然后我们通过将所有顶点视为中间顶点来更新解矩阵。思路是一一选取所有顶点并更新所有最短路径,其中包括选取的顶点作为最短路径中的中间顶点。当我们选择顶点编号 k 作为中间顶点时,我们已经将顶点 {0, 1, 2, .. k-1} 视为中间顶点。对于每对 (i, j) 的源顶点和目标顶点,分别有两种可能的情况。
1) k 不是从 i 到 j 的最短路径中的中间顶点。我们保持 dist[i][j] 的值不变。
2)k 是从 i 到 j 的最短路径中的中间顶点。我们将 dist[i][j] 的值更新为 dist[i][k] + dist[k][j] 如果 dist[i][j] > dist[i][k] + dist[k][ j]
下图显示了上述所有对最短路径问题中的最优子结构性质。

以下是 Floyd Warshall 算法的实现。
# Python Program for Floyd Warshall Algorithm
# Number of vertices in the graph
V = 4
# Define infinity as the large
# enough value. This value will be
# used for vertices not connected to each other
INF = 99999
# Solves all pair shortest path
# via Floyd Warshall Algorithm
def floydWarshall(graph):
""" dist[][] will be the output
matrix that will finally
have the shortest distances
between every pair of vertices """
""" initializing the solution matrix
same as input graph matrix
OR we can say that the initial
values of shortest distances
are based on shortest paths considering no
intermediate vertices """
dist = list(map(lambda i: list(map(lambda j: j, i)), graph))
""" Add all vertices one by one
to the set of intermediate
vertices.
---> Before start of an iteration,
we have shortest distances
between all pairs of vertices
such that the shortest
distances consider only the
vertices in the set
{0, 1, 2, .. k-1} as intermediate vertices.
----> After the end of a
iteration, vertex no. k is
added to the set of intermediate
vertices and the
set becomes {0, 1, 2, .. k}
"""
for k in range(V):
# pick all vertices as source one by one
for i in range(V):
# Pick all vertices as destination for the
# above picked source
for j in range(V):
# If vertex k is on the shortest path from
# i to j, then update the value of dist[i][j]
dist[i][j] = min(dist[i][j],
dist[i][k] + dist[k][j]
)
printSolution(dist)
# A utility function to print the solution
def printSolution(dist):
print "Following matrix shows the shortest distances\
between every pair of vertices"
for i in range(V):
for j in range(V):
if(dist[i][j] == INF):
print "%7s" % ("INF"),
else:
print "%7d\t" % (dist[i][j]),
if j == V-1:
print ""
# Driver program to test the above program
# Let us create the following weighted graph
"""
10
(0)------->(3)
| /|\
5 | |
| | 1
\|/ |
(1)------->(2)
3 """
graph = [[0, 5, INF, 10],
[INF, 0, 3, INF],
[INF, INF, 0, 1],
[INF, INF, INF, 0]
]
# Print the solution
floydWarshall(graph)
# This code is contributed by Mythri J L
Output:
Following matrix shows the shortest distances between every pair of vertices
0 5 8 9
INF 0 3 4
INF INF 0 1
INF INF INF 0
时间复杂度: O(V^3)
以上程序只打印最短距离。我们也可以通过将前驱信息存储在单独的 2D 矩阵中来修改解决方案以打印最短路径。
此外,INF 的值可以作为limits.h 中的INT_MAX,以确保我们处理最大可能值。当我们取INF为INT_MAX时,我们需要改变上面程序中的if条件,以避免算术溢出。
#define INF INT_MAX
......................................
if ( dist[i][k] != INF &&
dist[k][j] != INF &&
dist[i][k] + dist[k][j] < dist[i][j]
)
dist[i][j] = dist[i][k] + dist[k][j];
8.爬楼梯(Count ways to reach the n’th stair)(36)
有n个楼梯,站在底部的人想要到达顶部。该人一次可以爬 1 个楼梯或 2 个楼梯。计算多少种方法人能登顶。
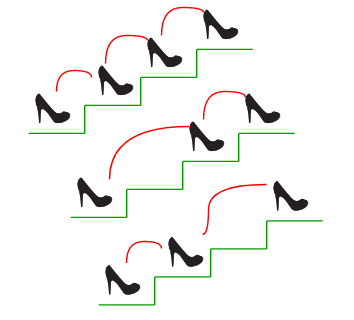
考虑图中所示的示例。n 的值为 3。有 3 种方法可以到达顶部。
Input: n = 1
Output: 1
There is only one way to climb 1 stair
Input: n = 2
Output: 2
There are two ways: (1, 1) and (2)
Input: n = 4
Output: 5
(1, 1, 1, 1), (1, 1, 2), (2, 1, 1), (1, 2, 1), (2, 2)
方法一:第一种方法使用递归技术来解决这个问题。
方法:我们可以很容易地发现上述问题中的递归性质。该人可达到nth可以从第(n-1)个台阶或从第(n-2)个台阶到达。因此,对于每个楼梯n,我们尝试找出到达(n-1)th台阶和(n-2)th台阶的方法数量,并将它们相加以给出nth楼梯的答案。因此,这种方法的表达式是:
ways(n) = ways(n-1) + ways(n-2)
上面的表达式实际上是斐波那契数的表达式,但是有一点需要注意,way(n) 的值等于 fibonacci(n+1)。
ways(1) = fib(2) = 1
ways(2) = fib(3) = 2
ways(3) = fib(4) = 3
为了更好地理解,让我们参考下面的递归树 -:
Input: N = 4
fib(5)
'3' / \ '2'
/ \
fib(4) fib(3)
'2' / \ '1' / \
/ \ / \
fib(3) fib(2)fib(2) fib(1)
/ \ '1' / \ '0'
'1' / '1'\ / \
/ \ fib(1) fib(0)
fib(2) fib(1)
所以我们可以使用斐波那契数的函数来找到 way(n) 的值
# Python program to count
# ways to reach nth stair
# Recursive function to find
# Nth fibonacci number
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
# Returns no. of ways to
# reach sth stair
def countWays(s):
return fib(s + 1)
# Driver program
s = 4
print "Number of ways = ",
print countWays(s)
# Contributed by Harshit Agrawal
输出:
方式数 = 5
复杂度分析:
- 时间复杂度: O(2^n)
由于冗余计算,上述实现的时间复杂度是指数级的(黄金比例增加到 n 次方)。可以使用前面讨论的 Fibonacci 函数优化优化以在 O(Logn) 时间内工作. - 辅助空间: O(1)
问题的概括
如果对于给定的值 m,一个人可以爬上 m 个楼梯,如何计算路径的数量。例如,如果 m 为 4,则此人一次可以爬 1 级或 2 级或 3 级或 4 级。
方法:对于上述方法的推广,可以使用以下递归关系。
way(n, m) = way(n-1, m) + way(n-2, m) + ... way(nm, m)
在这种到达nth个楼梯的方法中,尝试从当前楼梯爬上所有可能数量小于等于 n 的楼梯。
以下是上述递归的实现。
# A program to count the number of ways
# to reach n'th stair
# Recursive function used by countWays
def countWaysUtil(n, m):
if n <= 1:
return n
res = 0
i = 1
while i<= m and i<= n:
res = res + countWaysUtil(n-i, m)
i = i + 1
return res
# Returns number of ways to reach s'th stair
def countWays(s, m):
return countWaysUtil(s + 1, m)
# Driver program
s, m = 4, 2
print "Number of ways =", countWays(s, m)
# Contributed by Harshit Agrawal
输出:
方式数 = 5
复杂度分析:
- 时间复杂度: O(2^ n) 由于冗余计算,上述实现的时间复杂度是指数级的(黄金比例提高到 n 次方)。可以使用动态规划将其优化为 O(m*n)。
- 辅助空间: O(1)
方法 2:该方法使用动态规划技术来得出解决方案。
方法:我们使用以下关系以自下而上的方式创建一个表res[]:
res[i] = res[i] + res[i-j] for every (i-j) >= 0
使得ith数组的索引将包含的路的数目需要到达ith 步骤考虑攀登的所有可能性(即,从1到i)。
下面的代码实现了上述方法:
# A program to count the number of
# ways to reach n'th stair
# Recursive function used by countWays
def countWaysUtil(n, m):
# Creates list res with all elements 0
res = [0 for x in range(n)]
res[0], res[1] = 1, 1
for i in range(2, n):
j = 1
while j<= m and j<= i:
res[i] = res[i] + res[i-j]
j = j + 1
return res[n-1]
# Returns number of ways to reach s'th stair
def countWays(s, m):
return countWaysUtil(s + 1, m)
# Driver Program
s, m = 4, 2
print "Number of ways =", countWays(s, m)
# Contributed by Harshit Agrawal
输出:
方式数 = 5
复杂度分析:
- 时间复杂度: O(m*n)
- 辅助空间: O(n)
方法三:第三种方法是利用滑动窗口技术得出解。
方法:该方法有效地实现了上述动态规划方法。
在第i个楼梯的这种方法中,我们保留了最后m 个可能的楼梯总和的窗口,我们可以从中爬到第i个楼梯。我们没有运行内循环,而是将内循环的结果保存在一个临时变量中。我们删除前一个窗口的元素并添加当前窗口的元素并更新总和。
下面的代码实现了上面的想法
# Python3 program to count the number
# of ways to reach n'th stair when
# user climb 1 .. m stairs at a time.
# Function to count number of ways
# to reach s'th stair
def countWays(n, m):
temp = 0
res = [1]
for i in range(1, n + 1):
s = i - m - 1
e = i - 1
if (s >= 0):
temp -= res[s]
temp += res[e]
res.append(temp)
return res[n]
# Driver Code
n = 5
m = 3
print('Number of ways =', countWays(n, m))
# This code is contributed by 31ajaydandge
输出:
方式数 = 13
复杂度分析:
- 时间复杂度: O(n)
- 辅助空间: O(n)
方法 4:第四种方法使用简单的数学方法,但这仅适用于在计算步数时(顺序无关紧要)的问题。
方法:在这种方法中,我们简单地计算具有 2 的集合的数量。
n = 5
# Here n/2 is done to count the number 2's in n
# 1 is added for case where there is no 2.
# eg: if n=4 ans will be 3.
# {1,1,1,1} set having no 2.
# {1,1,2} ans {2,2} (n/2) sets containing 2.
print("Number of ways when order "
"of steps does not matter is : ", 1 + (n // 2))
# This code is contributed by rohitsingh07052
输出:
Number of ways when order of steps does not matter is : 3
复杂度分析:
- 时间复杂度:O(1)
- 空间复杂度:O(1)
注意:此方法只适用于Count way to N'th Stair(Order并不重要)的问题。
9.切割杆(Cutting a Rod)(13)
给定一根长度为 n 英寸的杆和一组价格,其中包括所有尺寸小于 n 的零件的价格。确定通过切割杆并出售碎片可获得的最大值。例如,如果杆的长度为 8,并且不同部分的值如下所示,则可获得的最大值为 22(通过切割长度为 2 和 6 的两段)
长度 | 1 2 3 4 5 6 7 8
-----------------------------------------------
价格 | 1 5 8 9 10 17 17 20
并且如果价格如下,那么最大可获得值是24(将8个长度剪成1个)
长度 | 1 2 3 4 5 6 7 8
-----------------------------------------------
价格 | 3 5 8 9 10 17 17 20
这个问题的一个简单的解决方案是生成不同部分的所有配置并找到价格最高的配置。该解决方案在时间复杂度方面呈指数级增长。让我们看看这个问题如何拥有动态规划 (DP) 问题的两个重要属性,并且可以使用动态规划有效地解决。
1)最优子结构:
我们可以通过在不同位置进行切割并比较切割后获得的值来获得最佳价格。我们可以为切割后获得的一块递归调用相同的函数。
令 cutRod(n) 是长度为 n 的杆所需的(最佳可能价格)值。cutRod(n) 可以写成如下。
cutRod(n) = max(price[i] + cutRod(ni-1)) 对于 {0, 1 .. n-1} 中的所有 i
2) 重叠子问题
下面是杆切割问题的简单递归实现。
实现只是遵循上面提到的递归结构。
输出
最大可获得值是 22
考虑到上述实现,以下是长度为 4 的 Rod 的递归树。
cR() ---> cutRod()
cR(4)
/ /
/ /
cR(3) cR(2) cR(1) cR(0)
/ | / |
/ | / |
cR(2) cR(1) cR(0) cR(1) cR(0) cR(0)
/ | |
/ | |
cR(1) cR(0) cR(0) cR(0)
/
/
CR(0)
在上面的部分递归树中,cR(2) 求解了两次。我们可以看到有很多子问题被一次又一次地解决了。由于再次调用相同的子问题,此问题具有重叠子问题的属性。因此,棒切割问题具有动态规划问题的两个性质。与其他典型的动态规划 (DP) 问题一样,可以通过以自底向上的方式构造临时数组 val[] 来避免对相同子问题的重新计算。
# A Dynamic Programming solution for Rod cutting problem
INT_MIN = -32767
# Returns the best obtainable price for a rod of length n and
# price[] as prices of different pieces
def cutRod(price, n):
val = [0 for x in range(n+1)]
val[0] = 0
# Build the table val[] in bottom up manner and return
# the last entry from the table
for i in range(1, n+1):
max_val = INT_MIN
for j in range(i):
max_val = max(max_val, price[j] + val[i-j-1])
val[i] = max_val
return val[n]
# Driver program to test above functions
arr = [1, 5, 8, 9, 10, 17, 17, 20]
size = len(arr)
print("Maximum Obtainable Value is " + str(cutRod(arr, size)))
# This code is contributed by Bhavya Jain
输出
最大可获得值是 22
上述实现的时间复杂度为O(n^2),比Naive Recursive实现的最坏情况时间复杂度要好很多。
3)利用无界背包的思想。
这个问题与无界背包问题非常相似,其中同一项目多次出现。这里是杆的碎片。
现在将在无界背包和杆切割问题之间进行类比。

# Python program for above approach
# Global Array for
# the purpose of memoization.
t = [[0 for i in range(9)] for j in range(9)]
# A recursive program, using ,
# memoization, to implement the
# rod cutting problem(Top-Down).
def un_kp(price, length, Max_len, n):
# The maximum price will be zero,
# when either the length of the rod
# is zero or price is zero.
if (n == 0 or Max_len == 0):
return 0;
# If the length of the rod is less
# than the maximum length, Max_lene will
# consider it.Now depending
# upon the profit,
# either Max_lene we will take
# it or discard it.
if (length[n - 1] <= Max_len):
t[n][Max_len] = max(price[n - 1] + un_kp(price, length, Max_len - length[n - 1], n),
un_kp(price, length, Max_len, n - 1));
# If the length of the rod is
# greater than the permitted size,
# Max_len we will not consider it.
else:
t[n][Max_len] = un_kp(price, length, Max_len, n - 1);
# Max_lene Max_lenill return the maximum
# value obtained, Max_lenhich is present
# at the nth roMax_len and Max_lenth column.
return t[n][Max_len];
if __name__ == '__main__':
price = [1, 5, 8, 9, 10, 17, 17, 20 ];
n =len(price);
length = [0]*n;
for i in range(n):
length[i] = i + 1;
Max_len = n;
print("Maximum obtained value is " ,un_kp(price, length, n, Max_len));
# This code is contributed by gauravrajput1
输出
获得的最大值为 22
10.编辑距离(Edit Distance)(5)
给定两个字符串 str1 和 str2 以及可以在 str1 上执行的操作。查找将“str1”转换为“str2”所需的最少编辑(操作)次数。
- 插入
- 消除
- 代替
以上所有操作都是等价的。
Examples:
Input: str1 = "geek", str2 = "gesek"
Output: 1
We can convert str1 into str2 by inserting a 's'.
Input: str1 = "cat", str2 = "cut"
Output: 1
We can convert str1 into str2 by replacing 'a' with 'u'.
Input: str1 = "sunday", str2 = "saturday"
Output: 3
Last three and first characters are same. We basically
need to convert "un" to "atur". This can be done using
below three operations.
Replace 'n' with 'r', insert t, insert a
这种情况下的子问题是什么?
这个想法是从两个字符串的左侧或右侧开始一个一个地处理所有字符。
让我们从右角开始遍历,每对被遍历的字符都有两种可能性。
m: Length of str1 (first string)
n: Length of str2 (second string)
- 如果两个字符串的最后一个字符相同,则没什么可做的。忽略最后一个字符并获取剩余字符串的计数。所以我们重复长度为 m-1 和 n-1。
- 否则(如果最后一个字符不相同),我们考虑对 'str1' 的所有操作,考虑对第一个字符串的最后一个字符的所有三个操作,递归计算所有三个操作的最小成本并取三个值的最小值。
- 插入:重复 m 和 n-1
- 删除:重复 m-1 和 n
- 替换:对 m-1 和 n-1 重复
以下是上述递归解决方案的实现。
# A Naive recursive Python program to fin minimum number
# operations to convert str1 to str2
def editDistance(str1, str2, m, n):
# If first string is empty, the only option is to
# insert all characters of second string into first
if m == 0:
return n
# If second string is empty, the only option is to
# remove all characters of first string
if n == 0:
return m
# If last characters of two strings are same, nothing
# much to do. Ignore last characters and get count for
# remaining strings.
if str1[m-1] == str2[n-1]:
return editDistance(str1, str2, m-1, n-1)
# If last characters are not same, consider all three
# operations on last character of first string, recursively
# compute minimum cost for all three operations and take
# minimum of three values.
return 1 + min(editDistance(str1, str2, m, n-1), # Insert
editDistance(str1, str2, m-1, n), # Remove
editDistance(str1, str2, m-1, n-1) # Replace
)
# Driver code
str1 = "sunday"
str2 = "saturday"
print editDistance(str1, str2, len(str1), len(str2))
# This code is contributed by Bhavya Jain
输出
3
上述解决方案的时间复杂度是指数级的。在最坏的情况下,我们可能最终会进行 O(3 m ) 次操作。最坏的情况发生在两个字符串的字符都不匹配时。下面是最坏情况的递归调用图。
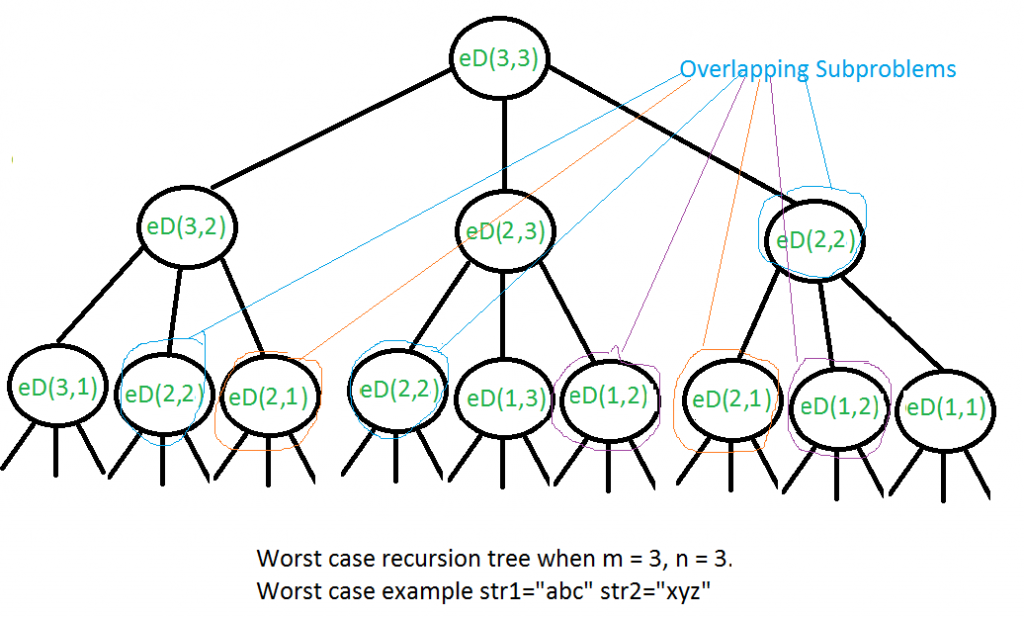
我们可以看到很多子问题都被解决了,一次又一次,例如eD(2, 2)被调用了3次。由于再次调用相同的子问题,该问题具有重叠子问题的性质。因此,编辑距离问题具有动态规划问题的两个属性。与其他典型的动态规划 (DP) 问题一样,可以通过构造一个存储子问题结果的临时数组来避免对相同子问题的重新计算。
# A Dynamic Programming based Python program for edit
# distance problem
def editDistDP(str1, str2, m, n):
# Create a table to store results of subproblems
dp = [[0 for x in range(n + 1)] for x in range(m + 1)]
# Fill d[][] in bottom up manner
for i in range(m + 1):
for j in range(n + 1):
# If first string is empty, only option is to
# insert all characters of second string
if i == 0:
dp[i][j] = j # Min. operations = j
# If second string is empty, only option is to
# remove all characters of second string
elif j == 0:
dp[i][j] = i # Min. operations = i
# If last characters are same, ignore last char
# and recur for remaining string
elif str1[i-1] == str2[j-1]:
dp[i][j] = dp[i-1][j-1]
# If last character are different, consider all
# possibilities and find minimum
else:
dp[i][j] = 1 + min(dp[i][j-1], # Insert
dp[i-1][j], # Remove
dp[i-1][j-1]) # Replace
return dp[m][n]
# Driver code
str1 = "sunday"
str2 = "saturday"
print(editDistDP(str1, str2, len(str1), len(str2)))
# This code is contributed by Bhavya Jain
输出
3
时间复杂度: O(m x n)
辅助空间: O(m x n)
空间复杂解决方案:在上面给出的方法中,我们需要 O(m x n) 空间。如果字符串的长度大于 2000,这将不合适,因为它只能创建 2000 x 2000 的二维数组。要填充 DP 数组中的一行,我们只需要上一行的一行。例如,如果我们在 DP 数组中填充 i = 10 行,我们只需要第 9 行的值。所以我们简单地创建一个 2 x str1 长度的 DP 数组。这种方法降低了空间复杂度。
# A Space efficient Dynamic Programming
# based Python3 program to find minimum
# number operations to convert str1 to str2
def EditDistDP(str1, str2):
len1 = len(str1)
len2 = len(str2)
# Create a DP array to memoize result
# of previous computations
DP = [[0 for i in range(len1 + 1)]
for j in range(2)];
# Base condition when second String
# is empty then we remove all characters
for i in range(0, len1 + 1):
DP[0][i] = i
# Start filling the DP
# This loop run for every
# character in second String
for i in range(1, len2 + 1):
# This loop compares the char from
# second String with first String
# characters
for j in range(0, len1 + 1):
# If first String is empty then
# we have to perform add character
# operation to get second String
if (j == 0):
DP[i % 2][j] = i
# If character from both String
# is same then we do not perform any
# operation . here i % 2 is for bound
# the row number.
elif(str1[j - 1] == str2[i-1]):
DP[i % 2][j] = DP[(i - 1) % 2][j - 1]
# If character from both String is
# not same then we take the minimum
# from three specified operation
else:
DP[i % 2][j] = (1 + min(DP[(i - 1) % 2][j],
min(DP[i % 2][j - 1],
DP[(i - 1) % 2][j - 1])))
# After complete fill the DP array
# if the len2 is even then we end
# up in the 0th row else we end up
# in the 1th row so we take len2 % 2
# to get row
print(DP[len2 % 2][len1], "")
# Driver code
if __name__ == '__main__':
str1 = "food"
str2 = "money"
EditDistDP(str1, str2)
# This code is contributed by gauravrajput1
输出
4
时间复杂度: O(mxn)
辅助空间: O(m)
这是递归的记忆版本,即自顶向下 DP:
def minDis(s1, s2, n, m, dp) :
# If any string is empty,
# return the remaining characters of other string
if(n == 0) :
return m
if(m == 0) :
return n
# To check if the recursive tree
# for given n & m has already been executed
if(dp[n][m] != -1) :
return dp[n][m];
# If characters are equal, execute
# recursive function for n-1, m-1
if(s1[n - 1] == s2[m - 1]) :
if(dp[n - 1][m - 1] == -1) :
dp[n][m] = minDis(s1, s2, n - 1, m - 1, dp)
return dp[n][m]
else :
dp[n][m] = dp[n - 1][m - 1]
return dp[n][m]
# If characters are nt equal, we need to
# find the minimum cost out of all 3 operations.
else :
if(dp[n - 1][m] != -1) :
m1 = dp[n - 1][m]
else :
m1 = minDis(s1, s2, n - 1, m, dp)
if(dp[n][m - 1] != -1) :
m2 = dp[n][m - 1]
else :
m2 = minDis(s1, s2, n, m - 1, dp)
if(dp[n - 1][m - 1] != -1) :
m3 = dp[n - 1][m - 1]
else :
m3 = minDis(s1, s2, n - 1, m - 1, dp)
dp[n][m] = 1 + min(m1, min(m2, m3))
return dp[n][m]
# Driver code
str1 = "voldemort"
str2 = "dumbledore"
n = len(str1)
m = len(str2)
dp = [[-1 for i in range(m + 1)] for j in range(n + 1)]
print(minDis(str1, str2, n, m, dp))
# This code is contributed by divyesh072019.
输出
7
11.子集和问题(Subset Sum Problem)(32)
给定一组非负整数和一个值sum,确定给定集合的子集是否存在 sum 等于给定sum的子集。
例子:
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True
There is a subset (4, 5) with sum 9.
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 30
Output: False
There is no subset that add up to 30.
方法一:递归。
方法:对于递归方法,我们将考虑两种情况。
- 考虑的最后一个元件和现在的所需金额=目标总和- “最后”元素的值和元素=总要素数- 1
- 保留“最后一个”元素,现在所需的总和 = 目标总和和元素数 = 总元素 – 1
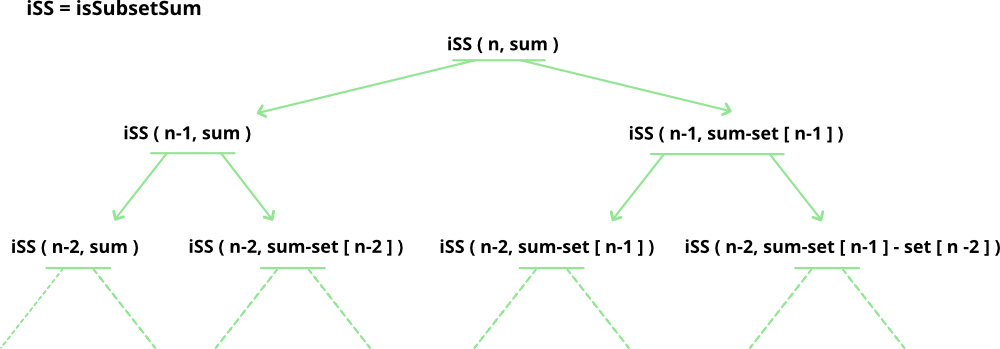
以下是 isSubsetSum() 问题的递归公式。
isSubsetSum(set, n, sum)
= isSubsetSum(set, n-1, sum) ||
isSubsetSum(set, n-1, sum-set[n-1])
Base Cases:
isSubsetSum(set, n, sum) = false, if sum > 0 and n == 0
isSubsetSum(set, n, sum) = true, if sum == 0
让我们来看看上述方法的模拟-:
set[]={3, 4, 5, 2}
sum=9
(x, y)= 'x' is the left number of elements,
'y' is the required sum
(4, 9)
{True}
/ \
(3, 6) (3, 9)
/ \ / \
(2, 2) (2, 6) (2, 5) (2, 9)
{True}
/ \
(1, -3) (1, 2)
{False} {True}
/ \
(0, 0) (0, 2)
{True} {False}
# A recursive solution for subset sum
# problem
# Returns true if there is a subset
# of set[] with sun equal to given sum
def isSubsetSum(set, n, sum):
# Base Cases
if (sum == 0):
return True
if (n == 0):
return False
# If last element is greater than
# sum, then ignore it
if (set[n - 1] > sum):
return isSubsetSum(set, n - 1, sum)
# else, check if sum can be obtained
# by any of the following
# (a) including the last element
# (b) excluding the last element
return isSubsetSum(
set, n-1, sum) or isSubsetSum(
set, n-1, sum-set[n-1])
# Driver code
set = [3, 34, 4, 12, 5, 2]
sum = 9
n = len(set)
if (isSubsetSum(set, n, sum) == True):
print("Found a subset with given sum")
else:
print("No subset with given sum")
# This code is contributed by Nikita Tiwari.
Output
Found a subset with given sum
复杂性分析:上述解决方案可能会在最坏情况下尝试给定集合的所有子集。因此上述解决方案的时间复杂度是指数级的。问题实际上是NP-Complete(此问题没有已知的多项式时间解决方案)。
方法2:使用动态规划解决伪多项式时间问题。
所以我们将创建一个大小为 (arr.size() + 1) * (target + 1) 的boolean类型的二维数组。如果存在来自 A[0.... i ] 且总和值 = 'j'的元素子集,则状态 DP[i][j] 将为真****。问题的处理方法是:
if (A[i-1] > j)
DP[i][j] = DP[i-1][j]
else
DP[i][j] = DP[i-1][j] OR DP[i-1][j-A[i-1]]
- 这意味着如果当前元素的值大于“当前总和值”,我们将复制以前案例的答案
- 如果当前的总和值大于 'ith' 元素,我们将查看是否有任何先前的状态已经经历过sum='j' 或任何先前的状态经历了一个值 'j – A[i]'这将解决我们的问题目的。
下面的模拟将阐明上述方法:
set[]={3, 4, 5, 2}
target=6
0 1 2 3 4 5 6
0 T F F F F F F
3 T F F T F F F
4 T F F T T F F
5 T F F T T T F
2 T F T T T T T
下面是上述方法的实现:
# A Dynamic Programming solution for subset
# sum problem Returns true if there is a subset of
# set[] with sun equal to given sum
# Returns true if there is a subset of set[]
# with sum equal to given sum
def isSubsetSum(set, n, sum):
# The value of subset[i][j] will be
# true if there is a
# subset of set[0..j-1] with sum equal to i
subset =([[False for i in range(sum + 1)]
for i in range(n + 1)])
# If sum is 0, then answer is true
for i in range(n + 1):
subset[i][0] = True
# If sum is not 0 and set is empty,
# then answer is false
for i in range(1, sum + 1):
subset[0][i]= False
# Fill the subset table in bottom up manner
for i in range(1, n + 1):
for j in range(1, sum + 1):
if j<set[i-1]:
subset[i][j] = subset[i-1][j]
if j>= set[i-1]:
subset[i][j] = (subset[i-1][j] or
subset[i - 1][j-set[i-1]])
# uncomment this code to print table
# for i in range(n + 1):
# for j in range(sum + 1):
# print (subset[i][j], end =" ")
# print()
return subset[n][sum]
# Driver code
if __name__=='__main__':
set = [3, 34, 4, 12, 5, 2]
sum = 9
n = len(set)
if (isSubsetSum(set, n, sum) == True):
print("Found a subset with given sum")
else:
print("No subset with given sum")
# This code is contributed by
# sahil shelangia.
Output
Found a subset with given sum
查找子集和的记忆技术:
方法:
- 在这种方法中,我们也遵循递归方法,但在这种方法中,我们使用另一个二维矩阵,首先用 -1 或任何负值进行初始化。
- 在这种方法中,我们避免了少数重复的递归调用,这就是我们使用二维矩阵的原因。在这个矩阵中,我们存储了前一个调用值的值。
下面是上述方法的实现:
# Python program for the above approach
# Taking the matrix as globally
tab = [[-1 for i in range(2000)] for j in range(2000)]
# Check if possible subset with
# given sum is possible or not
def subsetSum(a, n, sum):
# If the sum is zero it means
# we got our expected sum
if (sum == 0):
return 1
if (n <= 0):
return 0
# If the value is not -1 it means it
# already call the function
# with the same value.
# it will save our from the repetition.
if (tab[n - 1][sum] != -1):
return tab[n - 1][sum]
# if the value of a[n-1] is
# greater than the sum.
# we call for the next value
if (a[n - 1] > sum):
tab[n - 1][sum] = subsetSum(a, n - 1, sum)
return tab[n - 1][sum]
else:
# Here we do two calls because we
# don't know which value is
# full-fill our criteria
# that's why we doing two calls
tab[n - 1][sum] = subsetSum(a, n - 1, sum)
return tab[n - 1][sum] or subsetSum(a, n - 1, sum - a[n - 1])
# Driver Code
n = 5
a = [1, 5, 3, 7, 4]
sum = 12
if (subsetSum(a, n, sum)):
print("YES")
else:
print("NO")
# This code is contributed by shivani.
Output
YES
复杂度分析:
- 时间复杂度: O(sum*n),其中 sum 是“目标总和”,“n”是数组的大小。
- 辅助空间: O(sum*n),因为二维数组的大小是 sum*n。
12.最大和递增子序列(Maximum Sum Increasing Subsequence)(14)
给定一个由 n 个正整数组成的数组。编写一个程序,求给定数组的最大和子序列之和,使子序列中的整数按升序排列。例如,如果输入是{1, 101, 2, 3, 100, 4, 5},那么输出应该是106 (1 + 2 + 3 + 100),如果输入数组是{3, 4, 5, 10 },则输出应为 22 (3 + 4 + 5 + 10),如果输入数组为 {10, 5, 4, 3},则输出应为 10
解决方案
此问题是标准最长递增子序列(LIS) 问题的变体。我们需要对LIS 问题的动态规划解决方案稍作改动。我们需要改变的只是使用 sum 作为标准而不是增加子序列的长度。
以下是该问题的动态规划解决方案:
# Dynamic Programming bsed Python
# implementation of Maximum Sum
# Increasing Subsequence (MSIS)
# problem
# maxSumIS() returns the maximum
# sum of increasing subsequence
# in arr[] of size n
def maxSumIS(arr, n):
max = 0
msis = [0 for x in range(n)]
# Initialize msis values
# for all indexes
for i in range(n):
msis[i] = arr[i]
# Compute maximum sum
# values in bottom up manner
for i in range(1, n):
for j in range(i):
if (arr[i] > arr[j] and
msis[i] < msis[j] + arr[i]):
msis[i] = msis[j] + arr[i]
# Pick maximum of
# all msis values
for i in range(n):
if max < msis[i]:
max = msis[i]
return max
# Driver Code
arr = [1, 101, 2, 3, 100, 4, 5]
n = len(arr)
print("Sum of maximum sum increasing " +
"subsequence is " +
str(maxSumIS(arr, n)))
# This code is contributed
# by Bhavya Jain
Output :
Sum of maximum sum increasing subsequence is 106
时间复杂度:O(n^2)
空间复杂度 O(n)
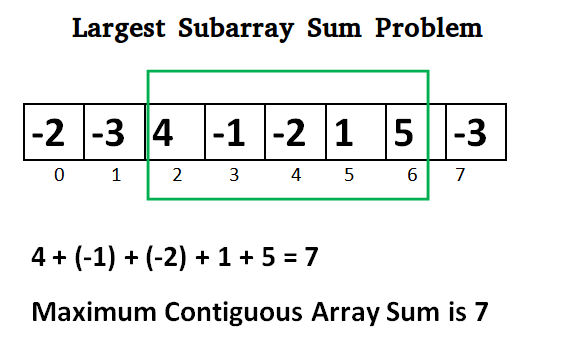
13.最大和连续子阵列(Largest Sum Contiguous Subarray)(27)
编写一个高效的程序,在具有最大和的一维数字数组中找到连续子数组的和。
Kadane 算法:
Initialize:
max_so_far = INT_MIN
max_ending_here = 0
Loop for each element of the array
(a) max_ending_here = max_ending_here + a[i]
(b) if(max_so_far < max_ending_here)
max_so_far = max_ending_here
(c) if(max_ending_here < 0)
max_ending_here = 0
return max_so_far
说明:
Kadane 算法的简单思想是寻找数组的所有正连续段(max_ending_here 用于此)。并跟踪所有正段中的最大和连续段(为此使用 max_so_far)。每次我们得到一个正和时,将它与 max_so_far 进行比较,如果它大于 max_so_far 则更新 max_so_far
Lets take the example:
{-2, -3, 4, -1, -2, 1, 5, -3}
max_so_far = max_ending_here = 0
for i=0, a[0] = -2
max_ending_here = max_ending_here + (-2)
Set max_ending_here = 0 because max_ending_here < 0
for i=1, a[1] = -3
max_ending_here = max_ending_here + (-3)
Set max_ending_here = 0 because max_ending_here < 0
for i=2, a[2] = 4
max_ending_here = max_ending_here + (4)
max_ending_here = 4
max_so_far is updated to 4 because max_ending_here greater
than max_so_far which was 0 till now
for i=3, a[3] = -1
max_ending_here = max_ending_here + (-1)
max_ending_here = 3
for i=4, a[4] = -2
max_ending_here = max_ending_here + (-2)
max_ending_here = 1
for i=5, a[5] = 1
max_ending_here = max_ending_here + (1)
max_ending_here = 2
for i=6, a[6] = 5
max_ending_here = max_ending_here + (5)
max_ending_here = 7
max_so_far is updated to 7 because max_ending_here is
greater than max_so_far
for i=7, a[7] = -3
max_ending_here = max_ending_here + (-3)
max_ending_here = 4
实现:
# Python program to find maximum contiguous subarray
# Function to find the maximum contiguous subarray
from sys import maxint
def maxSubArraySum(a,size):
max_so_far = -maxint - 1
max_ending_here = 0
for i in range(0, size):
max_ending_here = max_ending_here + a[i]
if (max_so_far < max_ending_here):
max_so_far = max_ending_here
if max_ending_here < 0:
max_ending_here = 0
return max_so_far
# Driver function to check the above function
a = [-13, -3, -25, -20, -3, -16, -23, -12, -5, -22, -15, -4, -7]
print "Maximum contiguous sum is", maxSubArraySum(a,len(a))
#This code is contributed by _Devesh Agrawal_
Output:
Maximum contiguous sum is 7
另一种方法:
def maxSubArraySum(a,size):
max_so_far = a[0]
max_ending_here = 0
for i in range(0, size):
max_ending_here = max_ending_here + a[i]
if max_ending_here < 0:
max_ending_here = 0
# Do not compare for all elements. Compare only
# when max_ending_here > 0
elif (max_so_far < max_ending_here):
max_so_far = max_ending_here
return max_so_far
时间复杂度: O(n)
算法范式:动态规划
以下是Mohit Kumar建议的另一个简单实现。该实现处理数组中所有数字都为负的情况。
# Python program to find maximum contiguous subarray
def maxSubArraySum(a,size):
max_so_far =a[0]
curr_max = a[0]
for i in range(1,size):
curr_max = max(a[i], curr_max + a[i])
max_so_far = max(max_so_far,curr_max)
return max_so_far
# Driver function to check the above function
a = [-2, -3, 4, -1, -2, 1, 5, -3]
print"Maximum contiguous sum is" , maxSubArraySum(a,len(a))
#This code is contributed by _Devesh Agrawal_
Output:
Maximum contiguous sum is 7
为了打印具有最大总和的子数组,我们在获得最大总和时维护索引。
# Python program to print largest contiguous array sum
from sys import maxsize
# Function to find the maximum contiguous subarray
# and print its starting and end index
def maxSubArraySum(a,size):
max_so_far = -maxsize - 1
max_ending_here = 0
start = 0
end = 0
s = 0
for i in range(0,size):
max_ending_here += a[i]
if max_so_far < max_ending_here:
max_so_far = max_ending_here
start = s
end = i
if max_ending_here < 0:
max_ending_here = 0
s = i+1
print ("Maximum contiguous sum is %d"%(max_so_far))
print ("Starting Index %d"%(start))
print ("Ending Index %d"%(end))
# Driver program to test maxSubArraySum
a = [-2, -3, 4, -1, -2, 1, 5, -3]
maxSubArraySum(a,len(a))
Output:
Maximum contiguous sum is 7
Starting index 2
Ending index 6
Kadane 算法可以被视为贪婪算法和 DP。正如我们所看到的,我们保持整数的运行总和,当它小于 0 时,我们将其重置为 0(贪婪部分)。这是因为继续负和比重新开始新范围要糟糕得多。现在它也可以被视为一个 DP,在每个阶段我们有 2 个选择:获取当前元素并继续之前的总和或重新启动一个新的范围。这两个选择都在实施中得到照顾。
时间复杂度: O(n)
辅助空间: O(1)
14.最小成本路径(Min Cost Path)(6)
给定成本矩阵 cost[][] 和在 cost[][] 中的位置 (m, n),编写一个函数,返回从 (0, 0) 到达 (m, n) 的最小成本路径的成本。矩阵的每个单元格表示遍历该单元格的成本。到达路径 (m, n) 的总成本是该路径上所有成本(包括源和目的地)的总和。您只能从给定的单元格向下、向右和斜下方的单元格遍历,即从给定的单元格 (i, j)、单元格 (i+1, j)、(i, j+1) 和 (i+1 , j+1) 可以遍历。您可以假设所有成本都是正整数。
例如,在下图中,到 (2, 2) 的最小成本路径是什么?
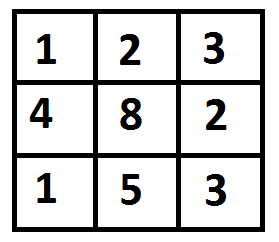
下图突出显示了成本最低的路径。路径是(0, 0) –> (0, 1) –> (1, 2) –> (2, 2)。路径的成本是 8 (1 + 2 + 2 + 3)。
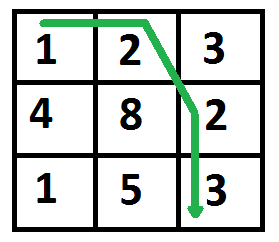
1)最优子结构
到达(m,n)的路径必须通过3个单元格之一:(m-1,n-1)或(m-1,n)或(m,n-1)。因此,达到 (m, n) 的最小成本可以写为“3 个单元的最小值加上成本 [m][n]”。
minCost(m, n) = min (minCost(m-1, n-1), minCost(m-1, n), minCost(m, n-1)) + cost[m][n]
2) 重叠子问题
以下是 MCP(最小成本路径)问题的简单递归实现。实现只是遵循上面提到的递归结构。
# A Naive recursive implementation of MCP(Minimum Cost Path) problem
R = 3
C = 3
import sys
# Returns cost of minimum cost path from (0,0) to (m, n) in mat[R][C]
def minCost(cost, m, n):
if (n < 0 or m < 0):
return sys.maxsize
elif (m == 0 and n == 0):
return cost[m][n]
else:
return cost[m][n] + min( minCost(cost, m-1, n-1),
minCost(cost, m-1, n),
minCost(cost, m, n-1) )
#A utility function that returns minimum of 3 integers */
def min(x, y, z):
if (x < y):
return x if (x < z) else z
else:
return y if (y < z) else z
# Driver program to test above functions
cost= [ [1, 2, 3],
[4, 8, 2],
[1, 5, 3] ]
print(minCost(cost, 2, 2))
# This code is contributed by
# Smitha Dinesh Semwal
输出
8
时间复杂度: O(m * n)
需要注意的是,上述函数一次又一次地计算相同的子问题。看下面的递归树,有很多节点出现了不止一次。这种朴素的递归解决方案的时间复杂度是指数级的,而且速度非常慢。
mC refers to minCost()
mC(2, 2)
/ | \
/ | \
mC(1, 1) mC(1, 2) mC(2, 1)
/ | \ / | \ / | \
/ | \ / | \ / | \
mC(0,0) mC(0,1) mC(1,0) mC(0,1) mC(0,2) mC(1,1) mC(1,0) mC(1,1) mC(2,0)
因此,MCP 问题具有动态规划问题的两个性质。与其他典型的动态规划 (DP) 问题一样,可以通过以自底向上的方式构造临时数组 tc 来避免对相同子问题的重新计算。
# Dynamic Programming Python implementation of Min Cost Path
# problem
R = 3
C = 3
def minCost(cost, m, n):
# Instead of following line, we can use int tc[m+1][n+1] or
# dynamically allocate memoery to save space. The following
# line is used to keep te program simple and make it working
# on all compilers.
tc = [[0 for x in range(C)] for x in range(R)]
tc[0][0] = cost[0][0]
# Initialize first column of total cost(tc) array
for i in range(1, m+1):
tc[i][0] = tc[i-1][0] + cost[i][0]
# Initialize first row of tc array
for j in range(1, n+1):
tc[0][j] = tc[0][j-1] + cost[0][j]
# Construct rest of the tc array
for i in range(1, m+1):
for j in range(1, n+1):
tc[i][j] = min(tc[i-1][j-1], tc[i-1][j], tc[i][j-1]) + cost[i][j]
return tc[m][n]
# Driver program to test above functions
cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3]]
print(minCost(cost, 2, 2))
# This code is contributed by Bhavya Jain
输出
8
DP 实现的时间复杂度为 O(mn),这比 Naive Recursive 实现要好得多。
辅助空间: O(m * n)
空间优化:想法是使用相同的给定数组来存储子问题的解决方案。
# Python3 program for the
# above approach
def minCost(cost, row, col):
# For 1st column
for i in range(1, row):
cost[i][0] += cost[i - 1][0]
# For 1st row
for j in range(1, col):
cost[0][j] += cost[0][j - 1]
# For rest of the 2d matrix
for i in range(1, row):
for j in range(1, col):
cost[i][j] += (min(cost[i - 1][j - 1],
min(cost[i - 1][j],
cost[i][j - 1])))
# Returning the value in
# last cell
return cost[row - 1][col - 1]
# Driver code
if __name__ == '__main__':
row = 3
col = 3
cost = [ [ 1, 2, 3 ],
[ 4, 8, 2 ],
[ 1, 5, 3 ] ]
print(minCost(cost, row, col));
# This code is contributed by Amit Katiyar
输出
8
时间复杂度: O(row * col)
辅助空间: O(1)
替代解决方案
我们也可以使用Dijkstra 的最短路径算法。下面是该方法的实现:
/* Minimum Cost Path using Dijkstra’s shortest path
algorithm with Min Heap by dinglizeng */
#include <stdio.h>
#include <queue>
#include <limits.h>
using namespace std;
/* define the number of rows and the number of columns */
#define R 4
#define C 5
/* 8 possible moves */
int dx[] = {1,-1, 0, 0, 1, 1,-1,-1};
int dy[] = {0, 0, 1,-1, 1,-1, 1,-1};
/* The data structure to store the coordinates of \\
the unit square and the cost of path from the top left. */
struct Cell{
int x;
int y;
int cost;
};
/* The compare class to be used by a Min Heap.
* The greater than condition is used as this
is for a Min Heap based on priority_queue.
*/
class mycomparison
{
public:
bool operator() (const Cell &lhs, const Cell &rhs) const
{
return (lhs.cost > rhs.cost);
}
};
/* To verify whether a move is within the boundary. */
bool isSafe(int x, int y){
return x >= 0 && x < R && y >= 0 && y < C;
}
/* This solution is based on Dijkstra’s shortest path algorithm
* For each unit square being visited, we examine all
possible next moves in 8 directions,
* calculate the accumulated cost of path for each
next move, adjust the cost of path of the adjacent
units to the minimum as needed.
* then add the valid next moves into a Min Heap.
* The Min Heap pops out the next move with the minimum
accumulated cost of path.
* Once the iteration reaches the last unit at the lower
right corner, the minimum cost path will be returned.
*/
int minCost(int cost[R][C], int m, int n) {
/* the array to store the accumulated cost
of path from top left corner */
int dp[R][C];
/* the array to record whether a unit
square has been visited */
bool visited[R][C];
/* Initialize these two arrays, set path cost
to maximum integer value, each unit as not visited */
for(int i = 0; i < R; i++) {
for(int j = 0; j < C; j++) {
dp[i][j] = INT_MAX;
visited[i][j] = false;
}
}
/* Define a reverse priority queue.
* Priority queue is a heap based implementation.
* The default behavior of a priority queue is
to have the maximum element at the top.
* The compare class is used in the definition of the Min Heap.
*/
priority_queue<Cell, vector<Cell>, mycomparison> pq;
/* initialize the starting top left unit with the
cost and add it to the queue as the first move. */
dp[0][0] = cost[0][0];
pq.push({0, 0, cost[0][0]});
while(!pq.empty()) {
/* pop a move from the queue, ignore the units
already visited */
Cell cell = pq.top();
pq.pop();
int x = cell.x;
int y = cell.y;
if(visited[x][y]) continue;
/* mark the current unit as visited */
visited[x][y] = true;
/* examine all non-visited adjacent units in 8 directions
* calculate the accumulated cost of path for
each next move from this unit,
* adjust the cost of path for each next adjacent
units to the minimum if possible.
*/
for(int i = 0; i < 8; i++) {
int next_x = x + dx[i];
int next_y = y + dy[i];
if(isSafe(next_x, next_y) && !visited[next_x][next_y]) {
dp[next_x][next_y] = min(dp[next_x][next_y],
dp[x][y] + cost[next_x][next_y]);
pq.push({next_x, next_y, dp[next_x][next_y]});
}
}
}
/* return the minimum cost path at the lower
right corner */
return dp[m][n];
}
/* Driver program to test above functions */
int main()
{
int cost[R][C] = { {1, 8, 8, 1, 5},
{4, 1, 1, 8, 1},
{4, 2, 8, 8, 1},
{1, 5, 8, 8, 1} };
printf(" %d ", minCost(cost, 3, 4));
return 0;
}
输出
7
与以最小路径成本寻找节点的全扫描相比,在该解决方案中使用反向优先级队列可以降低时间复杂度。DP实现的整体Time Complexity为O(mn),不考虑使用中的优先级队列,比Naive Recursive实现要好很多。
15.优化二叉搜索树(Optimal Binary Search Tree)(30)
给定搜索键的排序数组键[0.. n-1]和频率计数的数组freq[0.. n-1],其中freq[i]是键 [i]的搜索次数。构造所有键的二叉搜索树,使得所有搜索的总成本尽可能小。
让我们首先定义 BST 的成本。BST 节点的成本是该节点的级别乘以其频率。根的级别为 1。
例子:
Input: keys[] = {10, 12}, freq[] = {34, 50}
There can be following two possible BSTs
10 12
\ /
12 10
I II
Frequency of searches of 10 and 12 are 34 and 50 respectively.
The cost of tree I is 34*1 + 50*2 = 134
The cost of tree II is 50*1 + 34*2 = 118
Input: keys[] = {10, 12, 20}, freq[] = {34, 8, 50}
There can be following possible BSTs
10 12 20 10 20
\ / \ / \ /
12 10 20 12 20 10
\ / / \
20 10 12 12
I II III IV V
Among all possible BSTs, cost of the fifth BST is minimum.
Cost of the fifth BST is 1*50 + 2*34 + 3*8 = 142
1) 最优子结构:
可以使用以下公式递归计算 freq[i..j] 的最优成本。
我们需要计算optCost(0, n-1)才能找到结果。
上面公式的思路很简单,我们将所有节点都作为根一个一个地尝试(r在第二项中从i变化到j)。当我们以第 r 个节点为根时,我们递归地计算从 i 到 r-1 和 r+1 到 j 的最优成本。
我们添加从 i 到 j 的频率总和(参见上述公式中的第一项)
将 i 到 j 的频率总和相加的原因:
这可以分为 2 部分,一是 freq[r]+除 r 之外从 i 到 j 的所有元素的频率之和。添加术语 freq[r] 是因为它将是根,这意味着级别为 1,因此 freq[r]*1=freq[r]。现在真正的部分来了,我们正在添加剩余元素的频率,因为当我们以 r 为根时,除此之外的所有元素都比子问题中计算的低 1 级。让我说得更清楚一点,为了计算 optcost(i,j) 我们假设 r 为根并计算 opt(i,r-1)+opt(r+1,j) 的最小值i<=r<=j。对于每个子问题,我们选择一个节点作为根。但实际上,子问题根及其所有后代节点的级别将比父问题根的级别大 1。
2) 重叠子问题
以下是简单遵循上述递归结构的递归实现。
# A naive recursive implementation of
# optimal binary search tree problem
# A recursive function to calculate
# cost of optimal binary search tree
def optCost(freq, i, j):
# Base cases
if j < i: # no elements in this subarray
return 0
if j == i: # one element in this subarray
return freq[i]
# Get sum of freq[i], freq[i+1], ... freq[j]
fsum = Sum(freq, i, j)
# Initialize minimum value
Min = 999999999999
# One by one consider all elements as
# root and recursively find cost of
# the BST, compare the cost with min
# and update min if needed
for r in range(i, j + 1):
cost = (optCost(freq, i, r - 1) +
optCost(freq, r + 1, j))
if cost < Min:
Min = cost
# Return minimum value
return Min + fsum
# The main function that calculates minimum
# cost of a Binary Search Tree. It mainly
# uses optCost() to find the optimal cost.
def optimalSearchTree(keys, freq, n):
# Here array keys[] is assumed to be
# sorted in increasing order. If keys[]
# is not sorted, then add code to sort
# keys, and rearrange freq[] accordingly.
return optCost(freq, 0, n - 1)
# A utility function to get sum of
# array elements freq[i] to freq[j]
def Sum(freq, i, j):
s = 0
for k in range(i, j + 1):
s += freq[k]
return s
# Driver Code
if __name__ == '__main__':
keys = [10, 12, 20]
freq = [34, 8, 50]
n = len(keys)
print("Cost of Optimal BST is",
optimalSearchTree(keys, freq, n))
# This code is contributed by PranchalK
Output:
Cost of Optimal BST is 142
上述朴素递归方法的时间复杂度是指数级的。需要注意的是,上述函数一次又一次地计算相同的子问题。我们可以看到在以下 freq[1..4] 的递归树中重复了许多子问题。

由于再次调用相同的子问题,该问题具有重叠子问题的性质。因此,最优 BST 问题具有动态规划问题的两个属性(参见this和this)。与其他典型的动态规划 (DP) 问题一样,可以通过以自下而上的方式构造临时数组 cost 来避免对相同子问题的重新计算。
动态规划解决方案
以下是使用动态规划优化 BST 问题的 C/C++ 实现。我们使用辅助数组 cost[n][n] 来存储子问题的解。cost[0][n-1] 将保存最终结果。实现中的挑战是,必须首先填充所有对角线值,然后是位于对角线正上方线上的值。换句话说,我们必须首先填充所有 cost[i][i] 值,然后是所有 cost[i][i+1] 值,然后是所有 cost[i][i+2] 值。那么如何以这种方式填充2D数组> 实现中使用的想法与矩阵链乘法问题相同,我们使用变量'L'作为链长并逐个递增'L'。我们使用“i”和“L”的值计算列号“j”。
# Dynamic Programming code for Optimal Binary Search
# Tree Problem
INT_MAX = 2147483647
""" A Dynamic Programming based function that
calculates minimum cost of a Binary Search Tree. """
def optimalSearchTree(keys, freq, n):
""" Create an auxiliary 2D matrix to store
results of subproblems """
cost = [[0 for x in range(n)]
for y in range(n)]
""" cost[i][j] = Optimal cost of binary search
tree that can be formed from keys[i] to keys[j].
cost[0][n-1] will store the resultant cost """
# For a single key, cost is equal to
# frequency of the key
for i in range(n):
cost[i][i] = freq[i]
# Now we need to consider chains of
# length 2, 3, ... . L is chain length.
for L in range(2, n + 1):
# i is row number in cost
for i in range(n - L + 2):
# Get column number j from row number
# i and chain length L
j = i + L - 1
if i >= n or j >= n:
break
cost[i][j] = INT_MAX
# Try making all keys in interval
# keys[i..j] as root
for r in range(i, j + 1):
# c = cost when keys[r] becomes root
# of this subtree
c = 0
if (r > i):
c += cost[i][r - 1]
if (r < j):
c += cost[r + 1][j]
c += sum(freq, i, j)
if (c < cost[i][j]):
cost[i][j] = c
return cost[0][n - 1]
# A utility function to get sum of
# array elements freq[i] to freq[j]
def sum(freq, i, j):
s = 0
for k in range(i, j + 1):
s += freq[k]
return s
# Driver Code
if __name__ == '__main__':
keys = [10, 12, 20]
freq = [34, 8, 50]
n = len(keys)
print("Cost of Optimal BST is",
optimalSearchTree(keys, freq, n))
# This code is contributed by SHUBHAMSINGH10
Output:
Cost of Optimal BST is 142
注
1)上述方案的时间复杂度为 O(n^4)。通过预先计算频率总和而不是一次又一次地调用 sum() ,时间复杂度可以很容易地降低到 O(n^3)。
2)在上述解决方案中,我们只计算了最优成本。这些解决方案也可以很容易地修改以存储 BST 的结构。我们可以创建另一个大小为 n 的辅助数组来存储树的结构。我们需要做的就是将所选的 'r' 存储在最里面的循环中。
16.划分问题(Partition problem)(18)
划分问题是确定给定的集合是否可以划分为两个子集,使得两个子集中的元素之和相同。
例子:
arr[] = {1, 5, 11, 5}
Output: true
The array can be partitioned as {1, 5, 5} and {11}
arr[] = {1, 5, 3}
Output: false
The array cannot be partitioned into equal sum sets.
以下是解决这个问题的两个主要步骤:
1) 计算数组的总和。如果 sum 为奇数,则不能有两个子集的和相等,因此返回 false。
2) 若数组元素之和为偶数,则计算sum/2,找到sum等于sum/2的数组子集。
第一步很简单。第二步至关重要,它可以使用递归或动态规划来解决。
Recursive Solution 下面
是上面提到的第二步的递归性质。
Let isSubsetSum(arr, n, sum/2) be the function that returns true if
there is a subset of arr[0..n-1] with sum equal to sum/2
The isSubsetSum problem can be divided into two subproblems
a) isSubsetSum() without considering last element
(reducing n to n-1)
b) isSubsetSum considering the last element
(reducing sum/2 by arr[n-1] and n to n-1)
If any of the above subproblems return true, then return true.
isSubsetSum (arr, n, sum/2) = isSubsetSum (arr, n-1, sum/2) ||
isSubsetSum (arr, n-1, sum/2 - arr[n-1])
下面是上面代码的实现:
# A recursive Python3 program for
# partition problem
# A utility function that returns
# true if there is a subset of
# arr[] with sun equal to given sum
def isSubsetSum(arr, n, sum):
# Base Cases
if sum == 0:
return True
if n == 0 and sum != 0:
return False
# If last element is greater than sum, then
# ignore it
if arr[n-1] > sum:
return isSubsetSum(arr, n-1, sum)
''' else, check if sum can be obtained by any of
the following
(a) including the last element
(b) excluding the last element'''
return isSubsetSum(arr, n-1, sum) or isSubsetSum(arr, n-1, sum-arr[n-1])
# Returns true if arr[] can be partitioned in two
# subsets of equal sum, otherwise false
def findPartion(arr, n):
# Calculate sum of the elements in array
sum = 0
for i in range(0, n):
sum += arr[i]
# If sum is odd, there cannot be two subsets
# with equal sum
if sum % 2 != 0:
return false
# Find if there is subset with sum equal to
# half of total sum
return isSubsetSum(arr, n, sum // 2)
# Driver code
arr = [3, 1, 5, 9, 12]
n = len(arr)
# Function call
if findPartion(arr, n) == True:
print("Can be divided into two subsets of equal sum")
else:
print("Can not be divided into two subsets of equal sum")
# This code is contributed by shreyanshi_arun.
Output
Can be divided into two subsets of equal sum
时间复杂度: O(2^n) 在最坏的情况下,此解决方案为每个元素尝试两种可能性(包括或排除)。
动态规划解决方案
当元素的总和不太大时,可以使用动态规划解决问题。我们可以创建一个大小为 (sum/2 + 1)*(n+1) 的二维数组 part[][]。我们可以以自下而上的方式构建解决方案,使得每个填充的条目都具有以下属性
part[i][j] = true if a subset of {arr[0], arr[1], ..arr[j-1]} has sum
equal to i, otherwise false
# Dynamic Programming based python
# program to partition problem
# Returns true if arr[] can be
# partitioned in two subsets of
# equal sum, otherwise false
def findPartition(arr, n):
sum = 0
i, j = 0, 0
# calculate sum of all elements
for i in range(n):
sum += arr[i]
if sum % 2 != 0:
return false
part = [[True for i in range(n + 1)]
for j in range(sum // 2 + 1)]
# initialize top row as true
for i in range(0, n + 1):
part[0][i] = True
# initialize leftmost column,
# except part[0][0], as 0
for i in range(1, sum // 2 + 1):
part[i][0] = False
# fill the partition table in
# bottom up manner
for i in range(1, sum // 2 + 1):
for j in range(1, n + 1):
part[i][j] = part[i][j - 1]
if i >= arr[j - 1]:
part[i][j] = (part[i][j] or
part[i - arr[j - 1]][j - 1])
return part[sum // 2][n]
# Driver Code
arr = [3, 1, 1, 2, 2, 1]
n = len(arr)
# Function call
if findPartition(arr, n) == True:
print("Can be divided into two",
"subsets of equal sum")
else:
print("Can not be divided into ",
"two subsets of equal sum")
# This code is contributed
# by mohit kumar 29
Output
Can be divided into two subsets of equal sum
下图显示了分区表中的值。
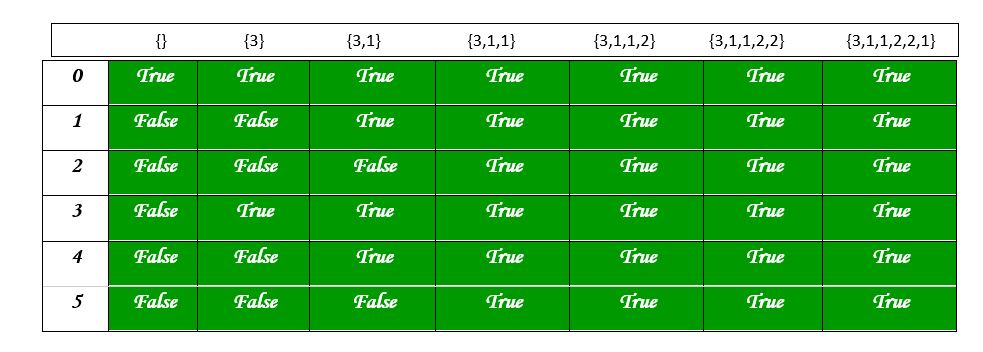
时间复杂度: O(sum*n)
辅助空间: O(sum*n)
17.斐波那契数列(Program for Fibonacci numbers)(23)
斐波那契数是以下整数序列中的数字。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .....
在数学上,斐波那契数列 Fn 由递推关系定义
Fn = Fn-1 + Fn-2 (F0 = 0 and F1 = 1.)
给定一个数 n,打印第 n 个斐波那契数。
例子:
Input : n = 2
Output : 1
Input : n = 9
Output : 34
编写一个返回 F n的函数int fib(int n)。例如,如果n = 0,那么fib()应该返回 0。如果 n = 1,那么它应该返回 1。对于 n > 1,它应该返回 F n-1 + F n-2
For n = 9
Output:34
以下是获取第 n 个斐波那契数的不同方法。
Method 1 (Use recursion)
一种简单的方法,是直接递归实现上面给出的数学递推关系。
# Function for nth Fibonacci number
def fib(n):
if n <= 1:
return n
if n > 0:
return fib(n-1) + fib(n-2)
if __name__ == "__main__":
print(fib(9))
# This code is contributed by Tdra
Output
34
时间复杂度: T(n) = T(n) 这是线性的。
如果要实现原始递归树,那么这将是树,但现在递归函数被调用了 n 次
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
上面代码的递归优化树:
fib(5)
fib(4)
fib(3)
fib(2)
fib(1)
额外空间:如果我们考虑函数调用堆栈大小,则为 O(n),否则为 O(1)。
方法 2(使用动态规划)
我们可以通过存储到目前为止计算的斐波那契数来避免方法 1 中所做的重复工作。
# Fibonacci Series using Dynamic Programming
def fibonacci(n):
# Taking 1st two fibonacci numbers as 0 and 1
f = [0, 1]
for i in range(2, n+1):
f.append(f[i-1] + f[i-2])
return f[n]
print(fibonacci(9))
Output
34
方法 3(空间优化方法 2)
我们可以通过存储前两个数字来优化方法 2 中使用的空间,因为这就是我们获得下一个斐波那契数列所需的全部内容。
# Function for nth fibonacci number - Space Optimisation
# Taking 1st two fibonacci numbers as 0 and 1
def fibonacci(n):
a = 0
b = 1
if n < 0:
print("Incorrect input")
elif n == 0:
return a
elif n == 1:
return b
else:
for i in range(2,n+1):
c = a + b
a = b
b = c
return b
# Driver Program
print(fibonacci(9))
#This code is contributed by Saket Modi
Output
34
时间复杂度: O(n)
额外空间: O(1)
方法 4(使用矩阵 {{1, 1}, {1, 0}} 的幂)
这是另一个 O(n),它依赖于如果我们将矩阵 M = {{1,1} 乘 n 次, {1,0}} 自身(换句话说,计算 power(M, n)),然后我们得到第 (n+1) 个斐波那契数作为结果矩阵中第 (0, 0) 行和第 (0, 0) 列的元素。
矩阵表示给出了以下斐波那契数列的封闭表达式:
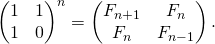
# Helper function that multiplies
# 2 matrices F and M of size 2*2,
# and puts the multiplication
# result back to F[][]
# Helper function that calculates
# F[][] raise to the power n and
# puts the result in F[][]
# Note that this function is
# designed only for fib() and
# won't work as general
# power function
def fib(n):
F = [[1, 1],
[1, 0]]
if (n == 0):
return 0
power(F, n - 1)
return F[0][0]
def multiply(F, M):
x = (F[0][0] * M[0][0] +
F[0][1] * M[1][0])
y = (F[0][0] * M[0][1] +
F[0][1] * M[1][1])
z = (F[1][0] * M[0][0] +
F[1][1] * M[1][0])
w = (F[1][0] * M[0][1] +
F[1][1] * M[1][1])
F[0][0] = x
F[0][1] = y
F[1][0] = z
F[1][1] = w
def power(F, n):
M = [[1, 1],
[1, 0]]
# n - 1 times multiply the
# matrix to {{1,0},{0,1}}
for i in range(2, n + 1):
multiply(F, M)
# Driver Code
if __name__ == "__main__":
n = 9
print(fib(n))
# This code is contributed
# by ChitraNayal
Output
34
时间复杂度: O(n)
额外空间: O(1)
方法 5(优化方法 4)
方法 4 可以优化为 O(Logn) 时间复杂度。我们可以做递归乘法来获得电力(M,N)在前面的方法
# Fibonacci Series using
# Optimized Method
# function that returns nth
# Fibonacci number
def fib(n):
F = [[1, 1],
[1, 0]]
if (n == 0):
return 0
power(F, n - 1)
return F[0][0]
def multiply(F, M):
x = (F[0][0] * M[0][0] +
F[0][1] * M[1][0])
y = (F[0][0] * M[0][1] +
F[0][1] * M[1][1])
z = (F[1][0] * M[0][0] +
F[1][1] * M[1][0])
w = (F[1][0] * M[0][1] +
F[1][1] * M[1][1])
F[0][0] = x
F[0][1] = y
F[1][0] = z
F[1][1] = w
# Optimized version of
# power() in method 4
def power(F, n):
if( n == 0 or n == 1):
return;
M = [[1, 1],
[1, 0]];
power(F, n // 2)
multiply(F, F)
if (n % 2 != 0):
multiply(F, M)
# Driver Code
if __name__ == "__main__":
n = 9
print(fib(n))
# This code is contributed
# by ChitraNayal
Output
34
时间复杂度: O(Logn)
额外空间:如果我们考虑函数调用堆栈大小,则为 O(Logn),否则为 O(1)。
│ D1_fractional_knapsack.py 斐波那契背包问题
│ D1_fractional_knapsack_2.py 斐波那契背包问题
│ D1_knapsack.py 背包问题
│ D2_longest_increasing_subsequence.py 最长递增子序列
│ D2_longest_increasing_subsequence_o(nlogn).py 最长递增子序列
│ D3_longest_common_subsequence.py 最长公共子序列
│ D4_minimum_coin_change.py 找零钱
│ D5_matrix_chain_order.py 矩阵链乘法
│ D7_floyd_warshall.py
│ D8_climbing_stairs.py 爬楼梯
│ D9_rod_cutting.py 切割杆
│ D10_edit_distance.py 最少编辑
│ D11_sum_of_subset.py 子集和
│ D12_max_sum_contiguous_subsequence.py 最大和递增子序列
│ D13_longest_sub_array.py 最大和连续子阵列
│ D13_max_sub_array.py 最大和连续子阵列
│ D14_minimum_cost_path.py 最小成本路径
│ D15_optimal_binary_search_tree.py 优化二叉搜索树
│ D16_integer_partition.py 整数划分
│ D16_minimum_partition.py 最小划分
│ D17_fast_fibonacci.py 斐波那契数列
│ D17_fibonacci.py 斐波那契数列
│ _init_.py
│ 动态规划DynamicProgramming.md




