1.2.3 回溯Tracebacking
回溯Tracebacking
- 回溯Tracebacking
- 1. 0-1背包问题(0-1 Knapsack Problem)
- 2.旅行商问题(TravelingSalesmanProblem,TSP)
- 3.N皇后问题(N Queen Problem)
- 4.迷宫问题(Rat in a Maze)
- 5.1全排列(All permutations)
- 5.2子集(Subset)
- 5.3组合(All combinations)
- 6.m着色问题(m Coloring Problem)
- 7.骑士的巡演问题(The Knight’s tour problem)
- 8.子集总和(Subset Sum)
- 9.数独(Sudoku)
- 10.哈密顿回路(Hamiltonian Cycle)
- 11.拔河比赛(Tug of War)
- 12.极小极大算法(Minimax)
1、概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
回溯法思路的简单描述就是:把问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解。
基本思想类同于:
- 图的深度优先搜索
-
二叉树的后序遍历
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
2、基本思想
回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树,当算法搜索至解空间树的某一节点时,先利用剪枝函数判断该节点是否可行(即能得到问题的解)。如果不可行,则跳过对该节点为根的子树的搜索,逐层向其祖先节点回溯;否则,进入该子树,继续按深度优先策略搜索。
回溯法的基本行为是搜索,搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类:1. 使用约束函数,剪去不满足约束条件的路径;2.使用限界函数,剪去不能得到最优解的路径。
问题的关键在于如何定义问题的解空间,转化成树(即解空间树)。解空间树分为两种:子集树和排列树。两种在算法结构和思路上大体相同。
3、用回溯法解题的一般步骤:
(1)针对所给问题,确定问题的解空间:
首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
(2)确定结点的扩展搜索规则
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
4、回溯法实现 - 递归和递推(迭代)
回溯法的实现方法有两种:递归和递推(也称迭代)。一般来说,一个问题两种方法都可以实现,只是在算法效率和设计复杂度上有区别。
【类比于图深度遍历的递归实现和非递归(递推)实现】
1). 递归
思路简单,设计容易,但效率低,其设计范式如下:
//针对N叉树的递归回溯方法
void backtrack (int t)
{
if (t>n) output(x); //叶子节点,输出结果,x是可行解
else
for i = 1 to k//当前节点的所有子节点
{
x[t]=value(i); //每个子节点的值赋值给x
//满足约束条件和限界条件
if (constraint(t)&&bound(t))
backtrack(t+1); //递归下一层
}
}
2). 递推
算法设计相对复杂,但效率高。
//针对N叉树的迭代回溯方法
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if(ExistSubNode(t)) //当前节点的存在子节点
{
for i = 1 to k //遍历当前节点的所有子节点
{
x[t]=value(i); //每个子节点的值赋值给x
if (constraint(t)&&bound(t))//满足约束条件和限界条件
{
//solution表示在节点t处得到了一个解
if (solution(t)) output(x); //得到问题的一个可行解,输出
else t++; //没有得到解,继续向下搜索
}
}
}
else //不存在子节点,返回上一层
{
t--;
}
}
}
子集树和排列树
1). 子集树
所给的问题是从n个元素的集合S中找出满足某种性质的子集时,相应的解空间成为子集树。
如0-1背包问题,从所给重量、价值不同的物品中挑选几个物品放入背包,使得在满足背包不超重的情况下,背包内物品价值最大。它的解空间就是一个典型的子集树。
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=0;i<=1;i++) {
x[t]=i;
if (constraint(t)&&bound(t)) backtrack(t+1);
}
}
2). 排列树
所给的问题是确定n个元素满足某种性质的排列时,相应的解空间就是排列树。
如旅行售货员问题,一个售货员把几个城市旅行一遍,要求走的路程最小。它的解就是几个城市的排列,解空间就是排列树。
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=t;i<=n;i++) {
swap(x[t], x[i]);
if (constraint(t)&&bound(t)) backtrack(t+1);
swap(x[t], x[i]);
}
}
1. 0-1背包问题(0-1 Knapsack Problem)
问题:给定n种物品和一背包。物品i的重量是wi,其价值为pi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
分析:问题是n个物品中选择部分物品,可知,问题的解空间是子集树。比如物品数目n=3时,其解空间树如下图,边为1代表选择该物品,边为0代表不选择该物品。使用x[i]表示物品i是否放入背包,x[i]=0表示不放,x[i]=1表示放入。回溯搜索过程,如果来到了叶子节点,表示一条搜索路径结束,如果该路径上存在更优的解,则保存下来。如果不是叶子节点,是中点的节点(如B),就遍历其子节点(D和E),如果子节点满足剪枝条件,就继续回溯搜索子节点。
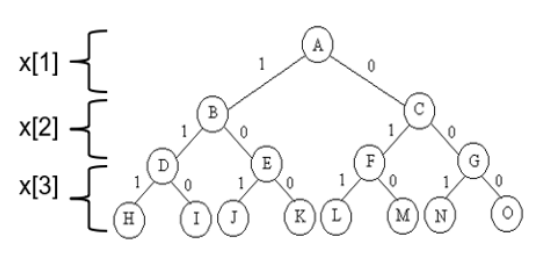
2.旅行商问题(TravelingSalesmanProblem,TSP)
旅行商问题(TravelingSalesmanProblem,TSP)是一个经典的组合优化问题。
经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。
从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列,随着顶点数的增加,会产生组合爆炸,它是一个NP完全问题。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用,国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题,常用的方法包括:分枝定界法、线性规划法、动态规划法等。但是,随着问题规模的增大,精确算法将变得无能为力,因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法,主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等
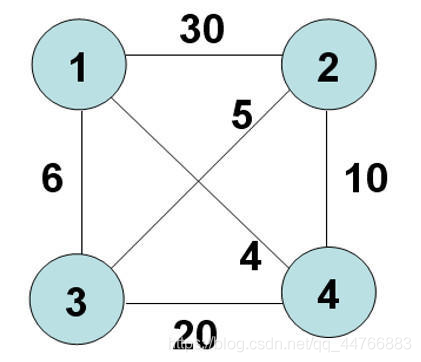
结果为: 1 3 2 4 1
算法描述
回溯法,序列树, 假设起点为 1。
算法开始时 x = [1, 2, 3, …, n]
x[1 : n]有两重含义 x[1 : i]代表前 i 步按顺序走过的城市, x[i + 1 : n]代表还未经过的城市。利用Swap函数进行交换位置。
若当前搜索的层次i = n 时,处在排列树的叶节点的父节点上,此时算法检查图G是否存在一条从顶点x[n-1] 到顶点x[n] 有一条边,和从顶点x[n] 到顶点x[1] 也有一条边。若这两条边都存在,则发现了一个旅行售货员的回路(即:新旅行路线),算法判断这条回路的费用是否优于已经找到的当前最优回路的费用bestcost,若是,则更新当前最优值bestcost和当前最优解bestx。
若i < n 时,检查x[i - 1]至x[i]之间是否存在一条边, 若存在,则x [1 : i ] 构成了图G的一条路径,若路径x[1: i] 的耗费小于当前最优解的耗费,则算法进入排列树下一层,否则剪掉相应的子树。
递归回溯
回溯法对解空间作深度优先搜索,通常用递归方法实现回溯法
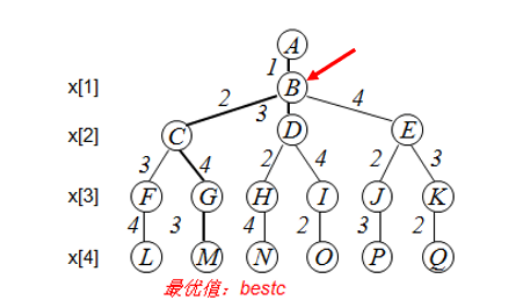
void backtrack (int t)
{
if (t>n) output(x);// t>n时已搜索到一个叶结点, output(x)对得到的可行解x进行记录或输出处理.
else{
// 函数f和g分别表示在当前扩展结点处未搜索子树的起止编号.
for (int i=f(n,t);i<=g(n,t);i++) {
x[t]=h(i); //h(i)表示在当前扩展结点处x[t]的第i个可选值
if (constraint(t)&&bound(t)) backtrack(t+1);
} //for循环结束后, 已搜索遍当前扩展结点的所有未搜索子树.
}
} //Backtrack(t)执行完毕, 返回t-1层继续执行, 对未测试过的x[t-1]的值继续搜索.
- if (Constraint(t)&&Bound(t) ) Backtrack(t + 1);if语句含义:Constraint(t)和Bound(t)表示当前扩展节点处的约束函数和限界函数。
- Constraint(t): 返回值为true时,在当前扩展节点处x[1:t]的取值问题的约束条件,否则不满足问题的约束条件,可剪去相应的子树
- Bound(t): 返回的值为true时,在当前扩展节点处x[1:t]的取值为时目标函数越界,还需由Backtrack(t+1)对其相应的子树做进一步搜索。否则,当前扩展节点处x[1:t]的取值是目标函数越界,可剪去相应的子树
- for循环作用:搜索遍当前扩展的所有未搜索过的子树。
- 递归出口:Backtrack(t)执行完毕,返回t-1层继续执行,对还没有测试过的x[t-1]的值继续搜索。当t=1时,若以测试完x[1]的所有可选值,外层调用就全部结束。
迭代回溯
采用树的非递归深度优先遍历算法,可将回溯法表示为一个非递归迭代过程。
void iterativeBacktrack ( )
{
int t=1;
while (t>0) {
if (f(n,t)<=g(n,t))
for (int i=f(n,t);i<=g(n,t);i++) {// 函数f和g分别表示在当前扩展结点处未搜索子树的起止编号.
x[t]=h(i);
if (constraint(t)&&bound(t)) {
if (solution(t)) output(x); //solution(t)判断当前扩展结点处是否已得到问题的一个可行解
else t++;} //solution(t)为假,则仅得到一个部分解,需继续纵深搜索
}
else t--;
} //while循环结束后,完成整个回溯搜索过程
}
3.N皇后问题(N Queen Problem)
N Queen 是将 N 个国际象棋皇后放在 N×N 棋盘上的问题,以便没有两个皇后互相攻击。例如,以下是 4 Queen 问题的解决方案。
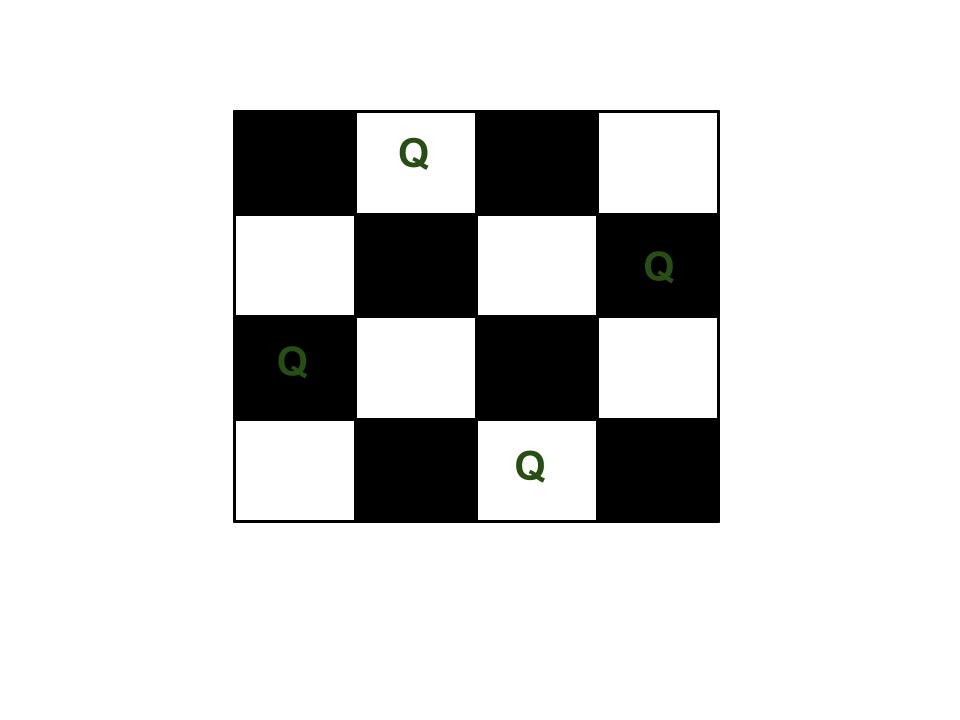
预期输出是一个二进制矩阵,其中放置皇后的块为 1。例如,以下是上述 4 Queen 解决方案的输出矩阵。
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
朴素算法
在船上生成所有可能的皇后配置并打印满足给定约束的配置。
while there are untried configurations
{
generate the next configuration
if queens don't attack in this configuration then
{
print this configuration;
}
}
回溯算法
的想法是将皇后一个一个地放置在不同的列中,从最左边的列开始。当我们将皇后放在一列中时,我们会检查与已经放置的皇后是否发生冲突。在当前列中,如果我们找到没有冲突的行,我们将此行和列标记为解决方案的一部分。如果由于冲突我们没有找到这样的行,那么我们回溯并返回 false。
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column.
Do following for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing the queen in [row, column] leads to
a solution then return true.
c) If placing queen doesn't lead to a solution then
unmark this [row, column] (Backtrack) and go to
step (a) to try other rows.
3) If all rows have been tried and nothing worked,
return false to trigger backtracking.
1) 从最左边的列开始
2) 如果所有皇后都被放置
返回真
3) 尝试当前列中的所有行。
对每个尝试过的行执行以下操作。
a) 如果皇后可以安全地放置在这一行
然后将此 [行,列] 标记为
解决方案并递归检查是否放置
女王在这里导致了一个解决方案。
b) 如果将皇后放在 [row, column] 导致
一个解决方案然后返回true。
c) 如果放置皇后不会导致解决方案,那么
取消标记此 [行,列](回溯)并转到
步骤 (a) 尝试其他行。
3)如果所有行都已尝试,但没有任何效果,
返回 false 以触发回溯。
# Python3 program to solve N Queen
# Problem using backtracking
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print (board[i][j], end = " ")
print()
# A utility function to check if a queen can
# be placed on board[row][col]. Note that this
# function is called when "col" queens are
# already placed in columns from 0 to col -1.
# So we need to check only left side for
# attacking queens
def isSafe(board, row, col):
# Check this row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1),
range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, N, 1),
range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed
# then return true
if col >= N:
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range(N):
if isSafe(board, i, col):
# Place this queen in board[i][col]
board[i][col] = 1
# recur to place rest of the queens
if solveNQUtil(board, col + 1) == True:
return True
# If placing queen in board[i][col
# doesn't lead to a solution, then
# queen from board[i][col]
board[i][col] = 0
# if the queen can not be placed in any row in
# this colum col then return false
return False
# This function solves the N Queen problem using
# Backtracking. It mainly uses solveNQUtil() to
# solve the problem. It returns false if queens
# cannot be placed, otherwise return true and
# placement of queens in the form of 1s.
# note that there may be more than one
# solutions, this function prints one of the
# feasible solutions.
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0] ]
if solveNQUtil(board, 0) == False:
print ("Solution does not exist")
return False
printSolution(board)
return True
# Driver Code
solveNQ()
# This code is contributed by Divyanshu Mehta
输出: 1 值表示皇后的位置
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
is_safe() 函数中
的优化思想不是检查左右对角线上的每个元素,而是使用对角线的属性:
- i 和 j 的总和对于每个右对角线都是常数和唯一的,其中 i 是元素的行,j是
元素的列。 - i 和 j 的差值对于每个左对角线都是常数和唯一的,其中 i 和 j 分别是元素的行和列。
回溯解决方案的实现(带优化)
""" Python3 program to solve N Queen Problem using
backtracking """
N = 4
""" ld is an array where its indices indicate row-col+N-1
(N-1) is for shifting the difference to store negative
indices """
ld = [0] * 30
""" rd is an array where its indices indicate row+col
and used to check whether a queen can be placed on
right diagonal or not"""
rd = [0] * 30
"""column array where its indices indicates column and
used to check whether a queen can be placed in that
row or not"""
cl = [0] * 30
""" A utility function to print solution """
def printSolution(board):
for i in range(N):
for j in range(N):
print(board[i][j], end = " ")
print()
""" A recursive utility function to solve N
Queen problem """
def solveNQUtil(board, col):
""" base case: If all queens are placed
then return True """
if (col >= N):
return True
""" Consider this column and try placing
this queen in all rows one by one """
for i in range(N):
""" Check if the queen can be placed on board[i][col] """
""" A check if a queen can be placed on board[row][col].
We just need to check ld[row-col+n-1] and rd[row+coln]
where ld and rd are for left and right diagonal respectively"""
if ((ld[i - col + N - 1] != 1 and
rd[i + col] != 1) and cl[i] != 1):
""" Place this queen in board[i][col] """
board[i][col] = 1
ld[i - col + N - 1] = rd[i + col] = cl[i] = 1
""" recur to place rest of the queens """
if (solveNQUtil(board, col + 1)):
return True
""" If placing queen in board[i][col]
doesn't lead to a solution,
then remove queen from board[i][col] """
board[i][col] = 0 # BACKTRACK
ld[i - col + N - 1] = rd[i + col] = cl[i] = 0
""" If the queen cannot be placed in
any row in this colum col then return False """
return False
""" This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns False if queens
cannot be placed, otherwise, return True and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions."""
def solveNQ():
board = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
if (solveNQUtil(board, 0) == False):
printf("Solution does not exist")
return False
printSolution(board)
return True
# Driver Code
solveNQ()
# This code is contributed by SHUBHAMSINGH10
输出: 1 值表示皇后的位置
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
4.迷宫问题(Rat in a Maze)
迷宫以块的 N*N 二进制矩)阵给出,其中源块是最左上的块,即 maze[0][0],目标块是最右下的块,即 maze[N-1][N-1] . 老鼠从源头出发,必须到达目的地。老鼠只能朝两个方向移动:向前和向下。
在迷宫矩阵中,0 表示该块是死胡同,1 表示该块可以在从源到目的地的路径中使用。请注意,这是典型迷宫问题的简单版本。例如,更复杂的版本可以是老鼠可以在 4 个方向上移动,而更复杂的版本可以是有限数量的移动。
以下是一个示例迷宫:

以下是上述迷宫的二进制矩阵表示。
{1, 0, 0, 0}
{1, 1, 0, 1}
{0, 1, 0, 0}
{1, 1, 1, 1}
以下是带有突出显示解决方案路径的迷宫。
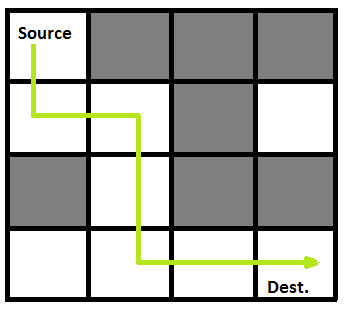
以下是上述输入矩阵的解矩阵(程序输出)。
{1, 0, 0, 0}
{1, 1, 0, 0}
{0, 1, 0, 0}
{0, 1, 1, 1}
解决方案路径中的所有条目都标记为 1。
回溯算法:回溯是一种通过尝试逐步构建解决方案来递归解决问题的算法技术。一次解决一个,并删除那些在任何时间点不满足问题约束的解决方案(这里的时间是指到达搜索树的任何级别所经过的时间)是回溯。
方法:形成一个递归函数,它会跟随一个路径并检查路径是否到达目的地。如果路径没有到达目的地,则回溯并尝试其他路径。
算法:
- 创建一个解决方案矩阵,最初填充为 0。
- 创建一个递归函数,它采用初始矩阵、输出矩阵和老鼠 (i, j) 的位置。
- 如果位置在矩阵之外或位置无效,则返回。
- 将位置 output[i][j] 标记为 1 并检查当前位置是否为目的地。如果到达目的地,则打印输出矩阵并返回。
- 递归调用位置 (i+1, j) 和 (i, j+1)。
- 取消标记位置 (i, j),即 output[i][j] = 0。
# Python3 program to solve Rat in a Maze
# problem using backracking
# Maze size
N = 4
# A utility function to print solution matrix sol
def printSolution( sol ):
for i in sol:
for j in i:
print(str(j) + " ", end ="")
print("")
# A utility function to check if x, y is valid
# index for N * N Maze
def isSafe( maze, x, y ):
if x >= 0 and x < N and y >= 0 and y < N and maze[x][y] == 1:
return True
return False
""" This function solves the Maze problem using Backtracking.
It mainly uses solveMazeUtil() to solve the problem. It
returns false if no path is possible, otherwise return
true and prints the path in the form of 1s. Please note
that there may be more than one solutions, this function
prints one of the feasable solutions. """
def solveMaze( maze ):
# Creating a 4 * 4 2-D list
sol = [ [ 0 for j in range(4) ] for i in range(4) ]
if solveMazeUtil(maze, 0, 0, sol) == False:
print("Solution doesn't exist");
return False
printSolution(sol)
return True
# A recursive utility function to solve Maze problem
def solveMazeUtil(maze, x, y, sol):
# if (x, y is goal) return True
if x == N - 1 and y == N - 1 and maze[x][y]== 1:
sol[x][y] = 1
return True
# Check if maze[x][y] is valid
if isSafe(maze, x, y) == True:
# Check if the current block is already part of solution path.
if sol[x][y] == 1:
return False
# mark x, y as part of solution path
sol[x][y] = 1
# Move forward in x direction
if solveMazeUtil(maze, x + 1, y, sol) == True:
return True
# If moving in x direction doesn't give solution
# then Move down in y direction
if solveMazeUtil(maze, x, y + 1, sol) == True:
return True
# If moving in y direction doesn't give solution then
# Move back in x direction
if solveMazeUtil(maze, x - 1, y, sol) == True:
return True
# If moving in backwards in x direction doesn't give solution
# then Move upwards in y direction
if solveMazeUtil(maze, x, y - 1, sol) == True:
return True
# If none of the above movements work then
# BACKTRACK: unmark x, y as part of solution path
sol[x][y] = 0
return False
# Driver program to test above function
if __name__ == "__main__":
# Initialising the maze
maze = [ [1, 0, 0, 0],
[1, 1, 0, 1],
[0, 1, 0, 0],
[1, 1, 1, 1] ]
solveMaze(maze)
# This code is contributed by Shiv Shankar
输出:
1 值显示了老鼠的路径
1 0 0 0
1 1 0 0
0 1 0 0
0 1 1 1
复杂度分析:
- 时间复杂度: O(2(n2))。
递归可以运行上限 2(n2) 次。 - 空间复杂度: O(n^2)。
需要输出矩阵,因此需要大小为 n*n 的额外空间。
5.1全排列(All permutations)
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
Input: [1,3,5]
Output: [1,3,5], [1,5,3], [3,1,5], [3,5,1], [5,1,3], [5,3,1]
解题思路:
结合回溯法的模式,需要特别考虑的是:
<满足条件>到达底层的条件就是选择列表nums为空
def permute(self, nums: List[int]) -> List[List[int]]:
# 函数输入为空时的特殊情况
if not nums: return nums
# 参数赋值初始化
res = []
tmp = []
# 调用backtrack函数,在类(class Solution)中要用self调用函数
self.backtrack(nums, tmp, res)
return res
# nums是选择列表,tmp是当前选择
def backtrack(self, nums, tmp, res):
#<满足条件> 到达底层的条件就是选择列表nums为空
if not nums:
# 错误写法 result.append(tem_result[]) 这样把地址传入,
# 后面回退的时候会是一堆空列表
res.append(tmp[:])
for i in range(len(nums)):
#<做出选择> 把选择列表中的元素append到当前选择中
tmp.append(nums[i])
# <backtrack(选择列表, 当前选择, 结果)>
# nums[0:i] + nums[i+1:] 把选的nums[i]去掉,更新选择列表nums
self.backtrack(nums[0:i] + nums[i+1:], tmp, res)
# <撤销选择> 调用结束即从下一层回溯到这一层,这时要更新当前选择tmp
tmp.pop()
5.2子集(Subset)
leetcode 78 (medium)给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
示例:
Input: [1, 5, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3]
方法一:回溯法,递归
解题思路
结合回溯法模式,需要特别考虑的是:
<满足条件>因为所有出现的当前列表都是子集,不用设置条件,把所有tmp加到res中
不能从选择列表中取所有元素,因为找子集只考虑当前元素之后的元素们,不能出现重复元素,所以要设起始点idx排除用过的元素,idx影响的是range的范围(选择列表)。递归调用时,因为 nums 不包含重复元素,并且每一个元素只能使用一次,所以下一次搜索从 i + 1 开始。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
if not nums: return None
res = []
self.backtrack(nums, [], res, 0)
return res
def backtrack(self, nums, tmp, res, idx):
# <满足条件>所有出现的当前列表都是子集,不用条件,直接append到res
res.append(tmp[:])
# 只考虑当前元素之后的元素们,要设起始点排除用过的元素
for i in range(idx, len(nums)):
# <做选择>
tmp.append(nums[i])
# <递归调用>
# 因为 nums 不包含重复元素,并且每一个元素只能使用一次,所以下一次搜索从 i + 1 开始
self.backtrack(nums, tmp, res, i+1)
# <撤销选择>
tmp.pop()
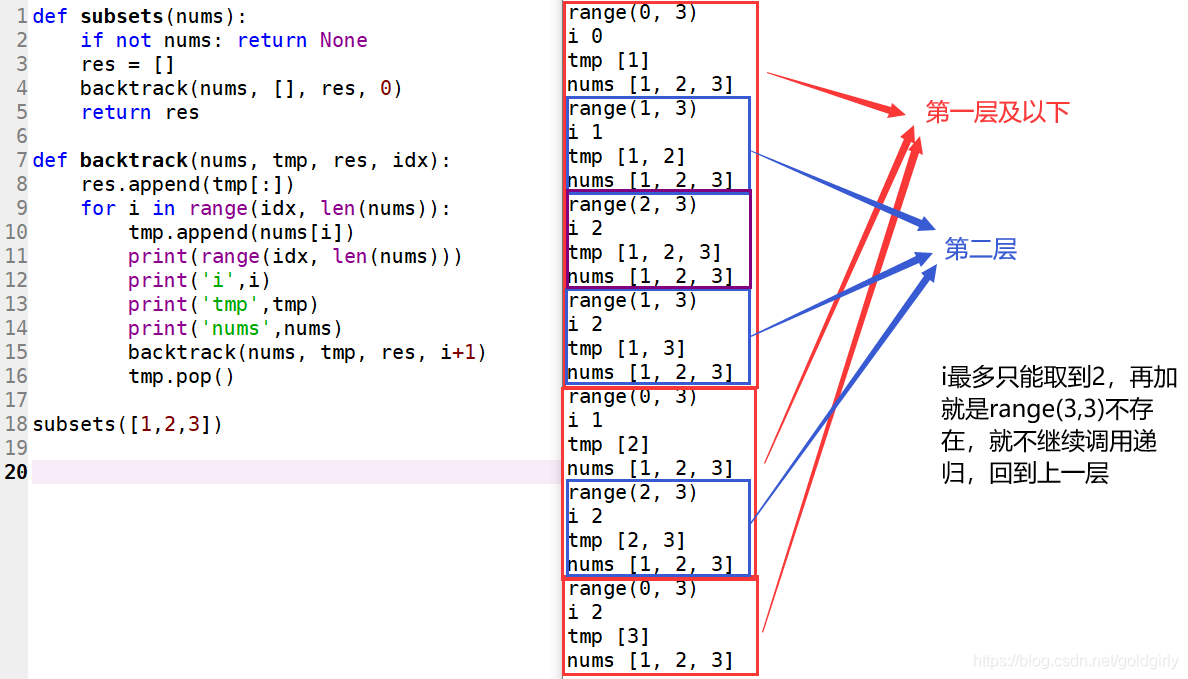
方法二:迭代
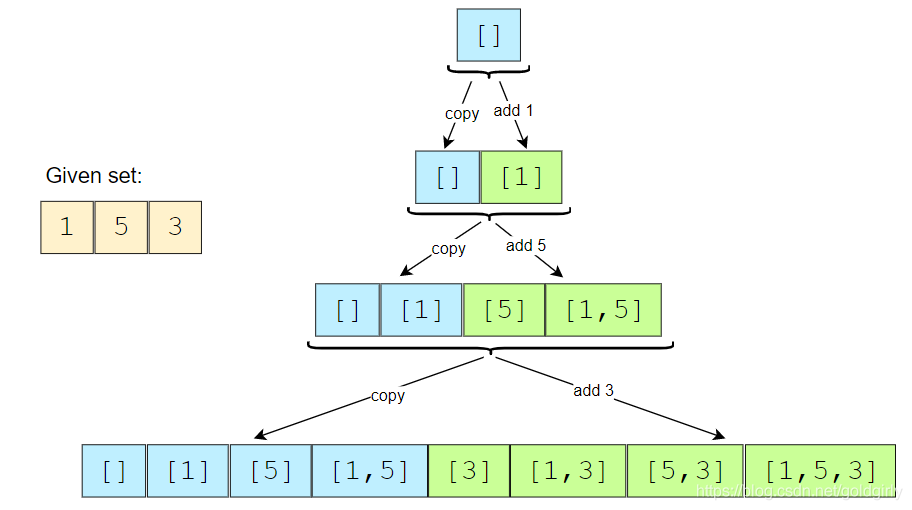
解题思路:
迭代,从空元素开始,循环每加入一个数组中的数值都相当于在上一个数组中的每项加入一个这个数值,再append到这个结果里![在这里插入图片描述]()
def subsets(nums):
res = []
res.append([])
# 大循环,取出数组内的每个元素
for i in nums:
#for j in res: #不要直接循环列表,用索引循环
# a = j.append(i) 这里j是列表,但不能这么写
# 小循环,取出结果的每个索引
for j in range(len(res)):
a = list(res[j])
# append大循环取出的元素
a.append(i) #不要写成b = a.append(a)
res.append(a)
return res
注意每次的小循环是循环subsets表中的元素(如上图第二层里的 [],[1]),取数组中的一个元素(如 5)append到[]里变成[5],然后再append到subsets表。
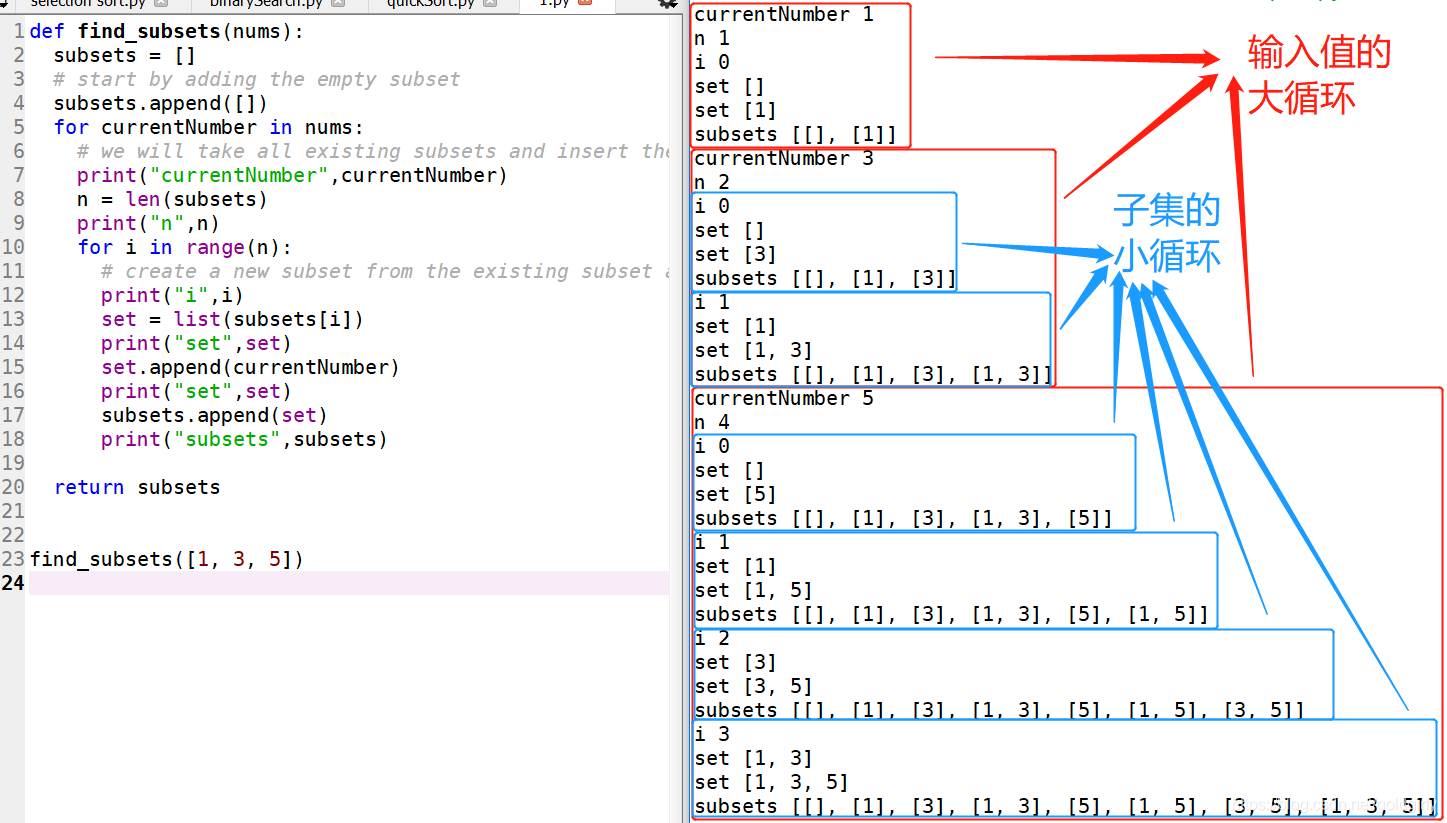
5.3组合(All combinations)
leetcode 77 (medium)给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
输入: n = 4, k = 2
输出: [[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]
解题思路:
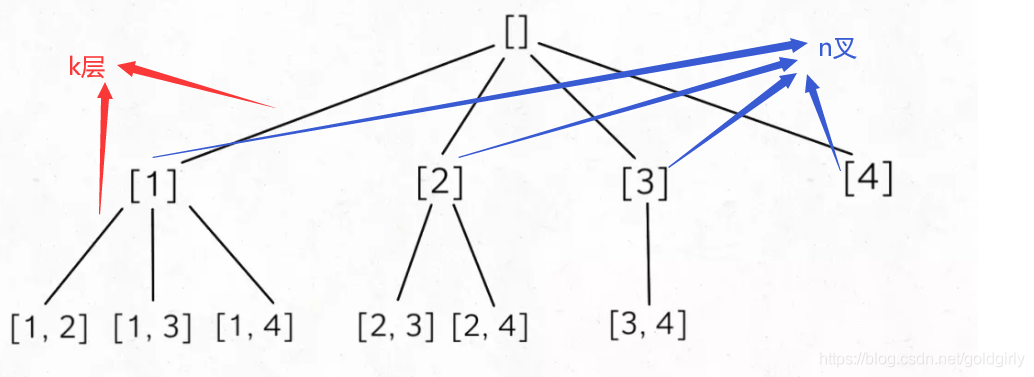
画出n叉树分析
![在这里插入图片描述]()
k 限制了树的高度,n 限制了树的宽度,想到k作为<满足条件>,n用来创建<选择列表>
跟子集一样,这里用过的元素不能再出现,要在range选择列表中设置起始点idx排除已经用过的元素
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
if not n or not k:
return None
nums = range(1, n+1)
res = []
self.backtrack(nums, [], res, k, 0)
return res
def backtrack(self, nums, tmp, res, k, idx):
# <满足条件> k限制树的高度,达到高度时加上当前列表tmp
if len(tmp) == k:
res.append(tmp[:])
# 参考子集的做法,设置起始点idx用来排除已经用过的元素
for i in range(idx, len(nums)):
# <做选择>
tmp.append(nums[i])
# <递归调用>
self.backtrack(nums, tmp, res, k, i+1)
# <撤销选择>
tmp.pop()
在框架基础上的一点优化,直接用n限制宽度
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
if not n or not k:
return None
res = []
self.backtrack(n, [], res, k, 1)
return res
def backtrack(self, n, tmp, res, k, idx):
if len(tmp) == k:
res.append(tmp[:])
# 优化代码:不用设nums,n就是nums的索引
for i in range(idx, n+1):
tmp.append(i)
self.backtrack(n, tmp, res, k, i+1)
tmp.pop()
6.m着色问题(m Coloring Problem)
给定一个无向图和一个数 m,确定该图是否最多可以用 m 种颜色进行着色,使得该图的两个相邻顶点不具有相同的颜色。这里的图着色意味着为所有顶点分配颜色。
输入:
- 二维数组 graph[V][V],其中 V 是图中顶点的数量,graph[V][V] 是图的邻接矩阵表示。如果从 i 到 j 存在直接边,则值 graph[i][j] 为 1,否则 graph[i][j] 为 0。
- 整数 m 是可以使用的最大颜色数。
输出:
一个数组 color[V],应该有从 1 到 m 的数字。color[i] 应该代表分配给第 i 个顶点的颜色。如果图形不能用 m 种颜色着色,代码也应该返回 false。
例子:
输入:
图 = {0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0}
输出:
解决方案存在:
以下是指定的颜色
1 2 3 2
说明:通过给顶点着色
具有以下颜色,相邻
顶点没有相同的颜色
输入:
图 = {1, 1, 1, 1},
{1, 1, 1, 1},
{1, 1, 1, 1},
{1, 1, 1, 1}
输出:解决方案不存在。
说明:没有解决方案存在。
以下是可以用 3 种不同颜色着色的图表示例:
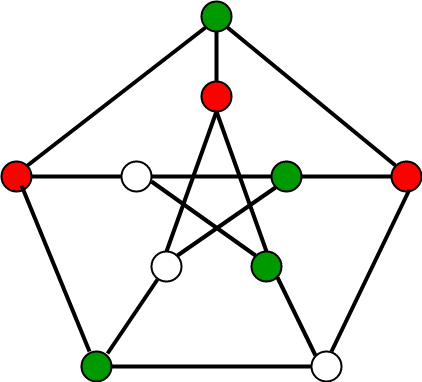
方法二: 回溯
方法:想法是从顶点0开始为不同的顶点一个一个地分配颜色。在分配颜色之前,通过考虑已经分配给相邻顶点的颜色来检查安全性,即检查相邻顶点是否具有相同的颜色. 如果有任何不违反条件的颜色分配,请将颜色分配标记为解决方案的一部分。如果无法分配颜色,则回溯并返回 false。
算法:
- 创建一个递归函数,该函数采用图形、当前索引、顶点数和输出颜色数组。
- 如果当前索引等于顶点数。在输出数组中打印颜色配置。
- 为顶点(1 到 m)指定颜色。
- 对于每个分配的颜色,检查配置是否安全,(即检查相邻顶点是否具有相同的颜色)递归调用具有下一个索引和顶点数的函数
- 如果任何递归函数返回真,则中断循环并返回真。
- 如果没有递归函数返回真,则返回假
# Python program for solution of M Coloring
# problem using backtracking
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]\
for row in range(vertices)]
# A utility function to check
# if the current color assignment
# is safe for vertex v
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
# A recursive utility function to solve m
# coloring problem
def graphColourUtil(self, m, colour, v):
if v == self.V:
return True
for c in range(1, m + 1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
if self.graphColourUtil(m, colour, v + 1) == True:
return True
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == None:
return False
# Print the solution
print "Solution exist and Following
are the assigned colours:"
for c in colour:
print c,
return True
# Driver Code
g = Graph(4)
g.graph = [[0, 1, 1, 1], [1, 0, 1, 0], [1, 1, 0, 1], [1, 0, 1, 0]]
m = 3
g.graphColouring(m)
# This code is contributed by Divyanshu Mehta
7.骑士的巡演问题(The Knight’s tour problem)
问题陈述:
给定一个 N*N 的棋盘,骑士被放置在一个空棋盘的第一个方块上。根据国际象棋骑士的规则移动必须恰好访问每个方格一次。打印访问它们的每个单元格的顺序。
例子:
输入 :
N = 8
输出:
0 59 38 33 30 17 8 63
37 34 31 60 9 62 29 16
58 1 36 39 32 27 18 7
35 48 41 26 61 10 15 28
42 57 2 49 40 23 6 19
47 50 45 54 25 20 11 14
56 43 52 3 22 13 24 5
51 46 55 44 53 4 21 12
Knight 覆盖所有单元格的路径 下面
是一个 8 x 8 单元格的棋盘。单元格中的数字表示骑士的移动数。
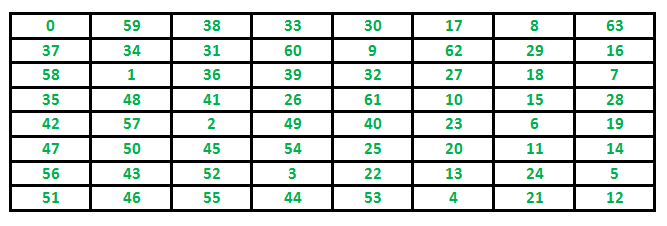
先讨论这个问题的 Naive 算法,然后讨论回溯算法。
Knight's tour
的朴素算法朴素算法是将所有的旅游一一生成,并检查生成的旅游是否满足约束条件。
while there are untried tours
{
generate the next tour
if this tour covers all squares
{
print this path;
}
}
回溯以增量方式解决问题。通常,我们从一个空的解向量开始,并一个一个地添加项目(项目的含义因问题而异。在 Knight's tour 问题的上下文中,一个项目是一个骑士的移动)。当我们添加一个项目时,我们检查添加当前项目是否违反了问题约束,如果是,那么我们删除该项目并尝试其他替代方案。如果没有一个替代方案可行,那么我们转到前一阶段并删除在前一阶段添加的项目。如果我们回到初始阶段,那么我们说不存在解决方案。如果添加一个项目不违反约束,那么我们递归地一个一个地添加项目。如果解向量变得完整,那么我们打印解。
骑士之旅的回溯算法
以下是奈特旅游问题的回溯算法。
If all squares are visited
print the solution
Else
a) Add one of the next moves to solution vector and recursively
check if this move leads to a solution. (A Knight can make maximum
eight moves. We choose one of the 8 moves in this step).
b) If the move chosen in the above step doesn't lead to a solution
then remove this move from the solution vector and try other
alternative moves.
c) If none of the alternatives work then return false (Returning false
will remove the previously added item in recursion and if false is
returned by the initial call of recursion then "no solution exists" )
以下是骑士旅游问题的实现。它以二维矩阵形式打印一种可能的解决方案。基本上,输出是一个 2D 8*8 矩阵,数字从 0 到 63,这些数字显示了 Knight 所做的步骤。
# Python3 program to solve Knight Tour problem using Backtracking
# Chessboard Size
n = 8
def isSafe(x, y, board):
'''
A utility function to check if i,j are valid indexes
for N*N chessboard
'''
if(x >= 0 and y >= 0 and x < n and y < n and board[x][y] == -1):
return True
return False
def printSolution(n, board):
'''
A utility function to print Chessboard matrix
'''
for i in range(n):
for j in range(n):
print(board[i][j], end=' ')
print()
def solveKT(n):
'''
This function solves the Knight Tour problem using
Backtracking. This function mainly uses solveKTUtil()
to solve the problem. It returns false if no complete
tour is possible, otherwise return true and prints the
tour.
Please note that there may be more than one solutions,
this function prints one of the feasible solutions.
'''
# Initialization of Board matrix
board = [[-1 for i in range(n)]for i in range(n)]
# move_x and move_y define next move of Knight.
# move_x is for next value of x coordinate
# move_y is for next value of y coordinate
move_x = [2, 1, -1, -2, -2, -1, 1, 2]
move_y = [1, 2, 2, 1, -1, -2, -2, -1]
# Since the Knight is initially at the first block
board[0][0] = 0
# Step counter for knight's position
pos = 1
# Checking if solution exists or not
if(not solveKTUtil(n, board, 0, 0, move_x, move_y, pos)):
print("Solution does not exist")
else:
printSolution(n, board)
def solveKTUtil(n, board, curr_x, curr_y, move_x, move_y, pos):
'''
A recursive utility function to solve Knight Tour
problem
'''
if(pos == n**2):
return True
# Try all next moves from the current coordinate x, y
for i in range(8):
new_x = curr_x + move_x[i]
new_y = curr_y + move_y[i]
if(isSafe(new_x, new_y, board)):
board[new_x][new_y] = pos
if(solveKTUtil(n, board, new_x, new_y, move_x, move_y, pos+1)):
return True
# Backtracking
board[new_x][new_y] = -1
return False
# Driver Code
if __name__ == "__main__":
# Function Call
solveKT(n)
# This code is contributed by AAKASH PAL
Output
0 59 38 33 30 17 8 63
37 34 31 60 9 62 29 16
58 1 36 39 32 27 18 7
35 48 41 26 61 10 15 28
42 57 2 49 40 23 6 19
47 50 45 54 25 20 11 14
56 43 52 3 22 13 24 5
51 46 55 44 53 4 21 12
时间复杂度:
有 N 2 个单元格,对于每个单元格,我们最多有 8 个可能的动作可供选择,因此最坏的运行时间是 O(8 N^2 )。
辅助空间: O(N 2 )
重要提示:
xMove、yMove 没有顺序是错误的,但是它们会极大地影响算法的运行时间。例如,考虑第 8 个选择是正确的移动的情况,在此之前我们的代码运行了 7 个不同的错误路径。使用启发式方法比尝试随机回溯总是一个好主意。就像,在这种情况下,我们知道下一步可能是向南或向东,然后检查引导他们第一个的路径是更好的策略。
请注意,回溯不是骑士游历问题的最佳解决方案。有关其他更好的解决方案,请参阅以下文章。这篇文章的目的是通过一个例子来解释回溯。
奈特旅游问题的 Warnsdorff 算法
8.子集总和(Subset Sum)
子集求和问题是找到从给定集合中选择的元素的子集,其总和为给定的数字 K。我们正在考虑该集合包含非负值。假设输入集是唯一的(不存在重复项)。
子集总和的穷举搜索算法
查找总和为 K 的子集的一种方法是考虑所有可能的子集。一发电机组包含所有那些从一组给定生成的子集。这种幂集的大小是 2 N。
子集总和的回溯算法
使用穷举搜索,我们考虑所有子集,而不管它们是否满足给定的约束。回溯可用于系统地考虑要选择的元素。
假设给定的 4 个元素集,比如说w[1] ... w[4]。树状图可用于设计回溯算法。下面的树图描述了生成可变大小元组的方法。
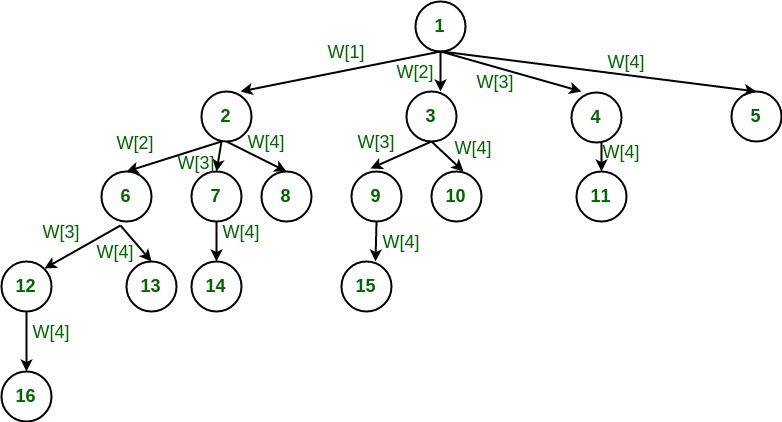
在上面的树中,一个节点代表函数调用,一个分支代表候选元素。根节点包含 4 个子节点。换句话说,root 将集合中的每个元素视为不同的分支。下一级子树对应于包含父节点的子集。每个级别的分支代表要考虑的元组元素。例如,如果我们处于第 1 级,则 tuple_vector[1] 可以采用生成的四个分支的任何值。如果我们在最左边节点的第 2 层,tuple_vector[2] 可以取生成的三个分支中的任意值,依此类推……
例如,root 的最左边的孩子生成所有包含 w[1] 的子集。类似地,root 的第二个孩子生成所有包含 w[2] 和排除 w[1] 的子集。
当我们沿着树的深度向下时,我们添加元素,如果添加的总和满足显式约束,我们将继续进一步生成子节点。每当不满足约束时,我们停止进一步生成该节点的子树,并回溯到前一个节点以探索尚未探索的节点。在许多情况下,它节省了大量的处理时间。
树应该触发一个线索来实现回溯算法(试试你自己)。它打印总和为给定数字的所有子集。我们需要沿着树的广度和深度探索节点。沿广度生成节点由循环控制,沿深度生成节点使用递归(后序遍历)。
if(subset is satisfying the constraint)
print the subset
exclude the current element and consider next element
else
generate the nodes of present level along breadth of tree and
recur for next levels
以下是使用可变大小元组向量的子集和的实现。请注意,以下程序探索了类似于穷举搜索的所有可能性。它是为了演示如何使用回溯。请参阅下一个代码以验证我们如何优化回溯解决方案。
的拼写错误
当我们结合显式和隐式约束时,回溯的威力就会显现出来,并且当这些检查失败时我们停止生成节点。我们可以通过加强约束检查和对数据进行预排序来改进上述算法。通过对初始数组进行排序,一旦到目前为止的总和大于目标数,我们就不需要考虑数组的其余部分。我们可以回溯并检查其他可能性。
类似地,假设数组是预先排序的,我们找到了一个子集。只有当包含下一个节点满足约束时,我们才能生成不包括当前节点的下一个节点。下面给出的是优化的实现(如果它不满足约束,它会修剪子树)。
#include <stdio.h>
#include <stdlib.h>
#define ARRAYSIZE(a) (sizeof(a))/(sizeof(a[0]))
static int total_nodes;
// prints subset found
void printSubset(int A[], int size)
{
for(int i = 0; i < size; i++)
{
printf("%*d", 5, A[i]);
}
printf("\n");
}
// qsort compare function
int comparator(const void *pLhs, const void *pRhs)
{
int *lhs = (int *)pLhs;
int *rhs = (int *)pRhs;
return *lhs > *rhs;
}
// inputs
// s - set vector
// t - tuplet vector
// s_size - set size
// t_size - tuplet size so far
// sum - sum so far
// ite - nodes count
// target_sum - sum to be found
void subset_sum(int s[], int t[],
int s_size, int t_size,
int sum, int ite,
int const target_sum)
{
total_nodes++;
if( target_sum == sum )
{
// We found sum
printSubset(t, t_size);
// constraint check
if( ite + 1 < s_size && sum - s[ite] + s[ite+1] <= target_sum )
{
// Exclude previous added item and consider next candidate
subset_sum(s, t, s_size, t_size-1, sum - s[ite], ite + 1, target_sum);
}
return;
}
else
{
// constraint check
if( ite < s_size && sum + s[ite] <= target_sum )
{
// generate nodes along the breadth
for( int i = ite; i < s_size; i++ )
{
t[t_size] = s[i];
if( sum + s[i] <= target_sum )
{
// consider next level node (along depth)
subset_sum(s, t, s_size, t_size + 1, sum + s[i], i + 1, target_sum);
}
}
}
}
}
// Wrapper that prints subsets that sum to target_sum
void generateSubsets(int s[], int size, int target_sum)
{
int *tuplet_vector = (int *)malloc(size * sizeof(int));
int total = 0;
// sort the set
qsort(s, size, sizeof(int), &comparator);
for( int i = 0; i < size; i++ )
{
total += s[i];
}
if( s[0] <= target_sum && total >= target_sum )
{
subset_sum(s, tuplet_vector, size, 0, 0, 0, target_sum);
}
free(tuplet_vector);
}
int main()
{
int weights[] = {15, 22, 14, 26, 32, 9, 16, 8};
int target = 53;
int size = ARRAYSIZE(weights);
generateSubsets(weights, size, target);
printf("Nodes generated %d\n", total_nodes);
return 0;
}
Output:
8 9 14 22n 8 14 15 16n 15 16 22nNodes generated 68
9.数独(Sudoku)
给定一个部分填充的 9×9 二维数组“grid[9][9]”,目标是将数字(从 1 到 9)分配给空单元格,以便每行、每列和大小为 3×3 的子网格都包含正好是从 1 到 9 的数字的一个实例。
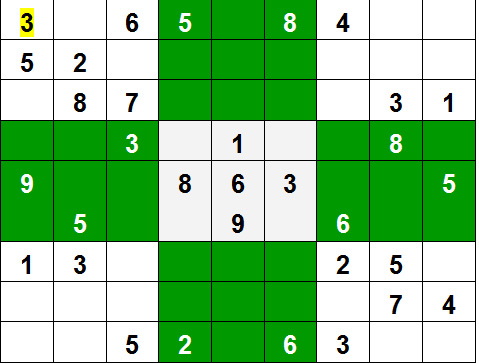
例子:
输入:
网格 = { {3, 0, 6, 5, 0, 8, 4, 0, 0},
{5, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 8, 7, 0, 0, 0, 0, 3, 1},
{0, 0, 3, 0, 1, 0, 0, 8, 0},
{9, 0, 0, 8, 6, 3, 0, 0, 5},
{0, 5, 0, 0, 9, 0, 6, 0, 0},
{1, 3, 0, 0, 0, 0, 2, 5, 0},
{0, 0, 0, 0, 0, 0, 0, 7, 4},
{0, 0, 5, 2, 0, 6, 3, 0, 0} }
输出:
3 1 6 5 7 8 4 9 2
5 2 9 1 3 4 7 6 8
4 8 7 6 2 9 5 3 1
2 6 3 4 1 5 9 8 7
9 7 4 8 6 3 1 2 5
8 5 1 7 9 2 6 4 3
1 3 8 9 4 7 2 5 6
6 9 2 3 5 1 8 7 4
7 4 5 2 8 6 3 1 9
说明:每行、每列和3*3盒
输出矩阵包含唯一的数字。
方法:最简单的方法是生成从 1 到 9 的所有可能的数字配置来填充空单元格。逐一尝试每个配置,直到找到正确的配置,即为每个未分配的位置填充一个从 1 到 9 的数字。填充所有未分配的位置后检查矩阵是否安全。如果安全打印,其他情况下会重复出现。
算法:
- 创建一个函数来检查给定的矩阵是否是有效的数独。保留行、列和框的 Hashmap。如果任何数字在 hashMap 中的频率大于 1,则返回 false,否则返回 true;
- 创建一个递归函数,它接受一个网格和当前的行和列索引。
- 检查一些基本情况。如果索引在矩阵的末尾,即 i=N-1 和 j=N 则检查网格是否安全,如果安全则打印网格并返回 true 否则返回 false。另一种基本情况是当列的值为 N 时,即 j = N,然后移动到下一行,即 i++ 和 j = 0。
- 如果未分配当前索引,则从 1 到 9 填充元素,并使用下一个元素的索引(即 i, j+1)对所有 9 种情况重复。如果递归调用返回true,则中断循环并返回true。
- 如果分配了当前索引,则使用下一个元素的索引调用递归函数,即 i, j+1
10.哈密顿回路(Hamiltonian Cycle)
无向图中的哈密顿路径是只访问每个顶点一次的路径。哈密顿回路(或哈密顿回路)是一条哈密顿路径,使得有一条边(在图中)从哈密顿路径的最后一个顶点到第一个顶点。确定给定的图是否包含哈密顿循环。如果包含,则打印路径。以下是所需函数的输入和输出。
输入:
一个二维数组 graph[V][V],其中 V 是图中顶点的数量,graph[V][V] 是图的邻接矩阵表示。如果存在从 i 到 j 的直接边,则值 graph[i][j] 为 1,否则 graph[i][j] 为 0。
输出:
应该包含哈密顿路径的数组路径[V]。path[i] 应该代表哈密顿路径中的第 i 个顶点。如果图中没有哈密顿循环,代码也应该返回 false。
例如,下图中的哈密顿环是 {0, 1, 2, 4, 3, 0}。
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3)-------(4)
下图不包含任何哈密顿循环。
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3) (4)
朴素算法
生成顶点的所有可能配置并打印满足给定约束的配置。会有n!(n 阶乘) 配置。
while there are untried conflagrations
{
generate the next configuration
if ( there are edges between two consecutive vertices of this
configuration and there is an edge from the last vertex to
the first ).
{
print this configuration;
break;
}
}
回溯算法
创建一个空的路径数组并添加顶点 0。添加其他顶点,从顶点开始 1. 添加顶点之前,检查它是否与之前添加的顶点相邻且尚未添加。如果我们找到这样的顶点,我们将添加该顶点作为解决方案的一部分。如果我们没有找到顶点,则返回 false。
# Python program for solution of
# hamiltonian cycle problem
class Graph():
def __init__(self, vertices):
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
self.V = vertices
''' Check if this vertex is an adjacent vertex
of the previously added vertex and is not
included in the path earlier '''
def isSafe(self, v, pos, path):
# Check if current vertex and last vertex
# in path are adjacent
if self.graph[ path[pos-1] ][v] == 0:
return False
# Check if current vertex not already in path
for vertex in path:
if vertex == v:
return False
return True
# A recursive utility function to solve
# hamiltonian cycle problem
def hamCycleUtil(self, path, pos):
# base case: if all vertices are
# included in the path
if pos == self.V:
# Last vertex must be adjacent to the
# first vertex in path to make a cyle
if self.graph[ path[pos-1] ][ path[0] ] == 1:
return True
else:
return False
# Try different vertices as a next candidate
# in Hamiltonian Cycle. We don't try for 0 as
# we included 0 as starting point in hamCycle()
for v in range(1,self.V):
if self.isSafe(v, pos, path) == True:
path[pos] = v
if self.hamCycleUtil(path, pos+1) == True:
return True
# Remove current vertex if it doesn't
# lead to a solution
path[pos] = -1
return False
def hamCycle(self):
path = [-1] * self.V
''' Let us put vertex 0 as the first vertex
in the path. If there is a Hamiltonian Cycle,
then the path can be started from any point
of the cycle as the graph is undirected '''
path[0] = 0
if self.hamCycleUtil(path,1) == False:
print ("Solution does not exist\n")
return False
self.printSolution(path)
return True
def printSolution(self, path):
print ("Solution Exists: Following",
"is one Hamiltonian Cycle")
for vertex in path:
print (vertex, end = " ")
print (path[0], "\n")
# Driver Code
''' Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3)-------(4) '''
g1 = Graph(5)
g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1],
[0, 1, 0, 0, 1,],[1, 1, 0, 0, 1],
[0, 1, 1, 1, 0], ]
# Print the solution
g1.hamCycle();
''' Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3) (4) '''
g2 = Graph(5)
g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1],
[0, 1, 0, 0, 1,], [1, 1, 0, 0, 0],
[0, 1, 1, 0, 0], ]
# Print the solution
g2.hamCycle();
# This code is contributed by Divyanshu Mehta
Output:
Solution Exists: Following is one Hamiltonian Cycle
0 1 2 4 3 0
Solution does not exist
请注意,上面的代码总是打印从 0 开始的循环。起点应该无关紧要,因为循环可以从任何点开始。如果你想改变起点,你应该对上面的代码做两处改动。
更改“路径[0] = 0;” 到“路径[0] = s;” 其中 s 是您的新起点。还将 hamCycleUtil() 中的循环“for (int v = 1; v < V; v++)”更改为“for (int v = 0; v < V; v++)”。
11.拔河比赛(Tug of War)
给定一组 n 个整数,将该集合分成两个大小分别为 n/2 的子集,以使两个子集之和的差异尽可能小。如果 n 为偶数,则两个子集的大小必须严格为 n/2;如果 n 为奇数,则一个子集的大小必须为 (n-1)/2,另一个子集的大小必须为 (n+1)/2 .
例如,让给定的集合为 {3, 4, 5, -3, 100, 1, 89, 54, 23, 20},集合的大小是 10。这个集合的输出应该是 {4, 100, 1, 23, 20} 和 {3, 5, -3, 89, 54}。两个输出子集的大小均为 5,并且两个子集中的元素总和相同(148 和 148)。
让我们考虑另一个 n 是奇数的例子。让给定集合为 {23, 45, -34, 12, 0, 98, -99, 4, 189, -1, 4}。输出子集应该是 {45, -34, 12, 98, -1} 和 {23, 0, -99, 4, 189, 4}。两个子集中的元素和分别为120和121。
以下解决方案尝试每个可能的半尺寸子集。如果形成一个半尺寸的子集,则其余元素形成另一个子集。我们将当前集合初始化为空并一一构建它。每个元素都有两种可能性,要么是当前集合的一部分,要么是剩余元素(其他子集)的一部分。我们考虑每个元素的两种可能性。当当前集合的大小变为 n/2 时,我们检查该解决方案是否优于目前可用的最佳解决方案。如果是,那么我们更新最佳解决方案。
# Python3 program for above approach
# function that tries every possible
# solution by calling itself recursively
def TOWUtil(arr, n, curr_elements, no_of_selected_elements,
soln, min_diff, Sum, curr_sum, curr_position):
# checks whether the it is going
# out of bound
if (curr_position == n):
return
# checks that the numbers of elements
# left are not less than the number of
# elements required to form the solution
if ((int(n / 2) - no_of_selected_elements) >
(n - curr_position)):
return
# consider the cases when current element
# is not included in the solution
TOWUtil(arr, n, curr_elements, no_of_selected_elements,
soln, min_diff, Sum, curr_sum, curr_position + 1)
# add the current element to the solution
no_of_selected_elements += 1
curr_sum = curr_sum + arr[curr_position]
curr_elements[curr_position] = True
# checks if a solution is formed
if (no_of_selected_elements == int(n / 2)):
# checks if the solution formed is better
# than the best solution so far
if (abs(int(Sum / 2) - curr_sum) < min_diff[0]):
min_diff[0] = abs(int(Sum / 2) - curr_sum)
for i in range(n):
soln[i] = curr_elements[i]
else:
# consider the cases where current
# element is included in the solution
TOWUtil(arr, n, curr_elements, no_of_selected_elements,
soln, min_diff, Sum, curr_sum, curr_position + 1)
# removes current element before returning
# to the caller of this function
curr_elements[curr_position] = False
# main function that generate an arr
def tugOfWar(arr, n):
# the boolean array that contains the
# inclusion and exclusion of an element
# in current set. The number excluded
# automatically form the other set
curr_elements = [None] * n
# The inclusion/exclusion array
# for final solution
soln = [None] * n
min_diff = [999999999999]
Sum = 0
for i in range(n):
Sum += arr[i]
curr_elements[i] = soln[i] = False
# Find the solution using recursive
# function TOWUtil()
TOWUtil(arr, n, curr_elements, 0,
soln, min_diff, Sum, 0, 0)
# Print the solution
print("The first subset is: ")
for i in range(n):
if (soln[i] == True):
print(arr[i], end = " ")
print()
print("The second subset is: ")
for i in range(n):
if (soln[i] == False):
print(arr[i], end = " ")
# Driver Code
if __name__ == '__main__':
arr = [23, 45, -34, 12, 0, 98,
-99, 4, 189, -1, 4]
n = len(arr)
tugOfWar(arr, n)
# This code is contributed by PranchalK
输出:
第一个子集是:45 -34 12 98 -1
第二个子集是:23 0 -99 4 189 4
时间复杂度: O(2^n)
计算机科学中最有趣的事情之一就是编写一个人机博弈的程序。有大量的例子,最出名的是编写一个国际象棋的博弈机器。但不管是什么游戏,程序趋向于遵循一个被称为Minimax算法,伴随着各种各样的子算法在一块。
12.极小极大算法(Minimax)
Minimax算法又名极小化极大算法,是一种找出失败的最大可能性中的最小值的算法。Minimax算法常用于棋类等由两方较量的游戏和程序,这类程序由两个游戏者轮流,每次执行一个步骤。我们众所周知的五子棋、象棋等都属于这类程序,所以说Minimax算法是基于搜索的博弈算法的基础。该算法是一种零总和算法,即一方要在可选的选项中选择将其优势最大化的选择,而另一方则选择令对手优势最小化的方法。
- Minimax是一种悲观算法,即假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向,即对手具有完美决策能力。因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的,也就是让对方在完美决策下所对我造成的损失最小。
- Minimax不找理论最优解,因为理论最优解往往依赖于对手是否足够愚蠢,Minimax中我方完全掌握主动,如果对方每一步决策都是完美的,则我方可以达到预计的最小损失格局,如果对方没有走出完美决策,则我方可能达到比预计的最悲观情况更好的结局。总之我方就是要在最坏情况中选择最好的。
实例分析:
现在考虑这样一个游戏:有三个盘子A、B和C,每个盘子分别放有三张纸币。A放的是1、20、50;B放的是5、10、100;C放的是1、5、20。单位均为“元”。有甲、乙两人,两人均对三个盘子和上面放置的纸币有可以任意查看。游戏分三步:
- 甲从三个盘子中选取一个。
- 乙从甲选取的盘子中拿出两张纸币交给甲。
- 甲从乙所给的两张纸币中选取一张,拿走。
其中甲的目标是最后拿到的纸币面值尽量大,乙的目标是让甲最后拿到的纸币面值尽量小。
基本思路
一般解决博弈类问题的自然想法是将格局组织成一棵树,树的每一个节点表示一种格局,而父子关系表示由父格局经过一步可以到达子格局。Minimax也不例外,它通过对以当前格局为根的格局树搜索来确定下一步的选择。而一切格局树搜索算法的核心都是对每个格局价值的评价。
解题
下图是上述示例问题的格局树:
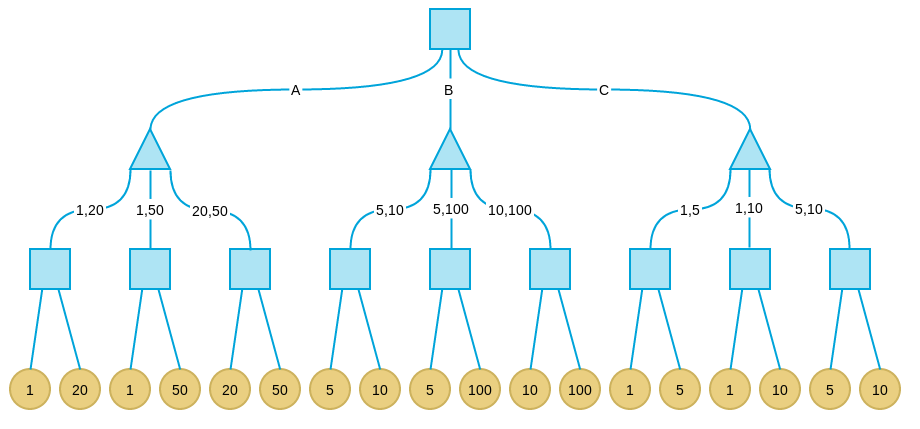
注意,由于示例问题格局数非常少,我们可以给出完整的格局树。这种情况下我可以找到Minimax算法的全局最优解。而真实情况中,格局树非常庞大,即使是计算机也不可能给出完整的树,因此我们往往只搜索一定深度,这时只能找到局部最优解。
我们从甲的角度考虑。其中正方形节点表示轮到我方(甲),而三角形表示轮到对方(乙)。经过三轮对弈后(我方-对方-我方),将进入终局。黄色叶结点表示所有可能的结局。从甲方看,由于最终的收益可以通过纸币的面值评价,我们自然可以用结局中甲方拿到的纸币面值表示终格局的价值。
下面考虑倒数第二层节点,在这些节点上,轮到我方选择,所以我们应该引入可选择的最大价值格局,因此每个节点的价值为其子节点的最大值:
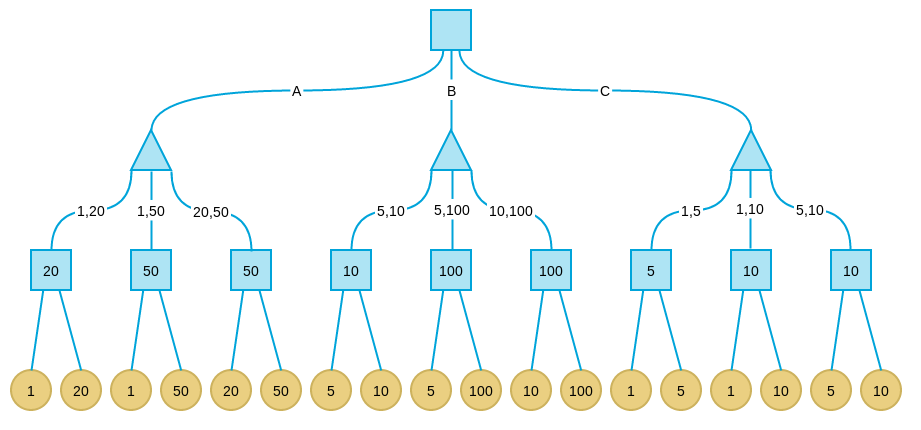
这些轮到我方的节点叫做max节点,max节点的值是其子节点最大值。
倒数第三层轮到对方选择,假设对方会尽力将局势引入让我方价值最小的格局,因此这些节点的价值取决于子节点的最小值。 这些轮到对方的节点叫做min节点。
最后,根节点是max节点,因此价值取决于叶子节点的最大值。最终完整赋值的格局树如下:
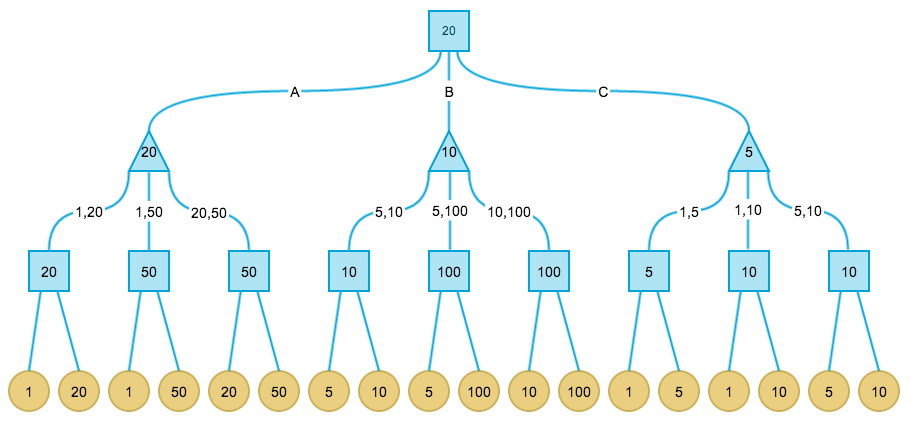
总结一下Minimax算法的步骤:
- 首先确定最大搜索深度D,D可能达到终局,也可能是一个中间格局。
- 在最大深度为D的格局树叶子节点上,使用预定义的价值评价函数对叶子节点价值进行评价。
- 自底向上为非叶子节点赋值。其中max节点取子节点最大值,min节点取子节点最小值
- 每次轮到我方时(此时必处在格局树的某个max节点),选择价值等于此max节点价值的那个子节点路径。
在上面的例子中,根节点的价值为20,表示如果对方每一步都完美决策,则我方按照上述算法可最终拿到20元,这是我方在Minimax算法下最好的决策。格局转换路径如下图红色路径所示:
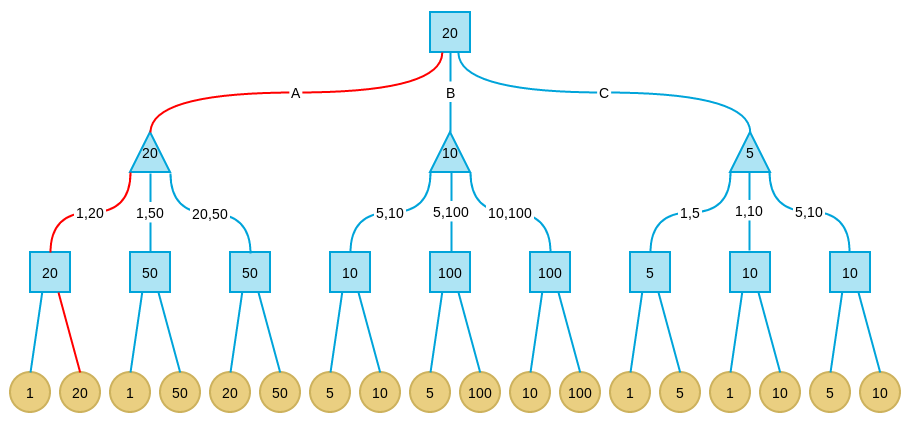
强调几点:
- 真实问题一般无法构造出完整的格局树,所以需要确定一个最大深度D,每次最多从当前格局向下计算D层。
- 因为上述原因,Minimax一般是寻找一个局部最优解而不是全局最优解,搜索深度越大越可能找到更好的解,但计算耗时会呈指数级膨胀。
- 也是因为无法一次构造出完整的格局树,所以真实问题中Minimax一般是边对弈边计算局部格局树,而不是只计算一次,但已计算的中间结果可以缓存。
│ b1_all_combinations.py 所有组合
│ b1_all_permutations.py 所有排列
│ b1_all_subsequences.py 所有子序列
│ b1_sum_of_subsets.py 子集和
│ b2_n_queens.py N皇后
│ b2_n_queens_math.py N皇后
│ b3_rat_in_maze.py 迷宫
│ b4_knight_tour.py 骑士巡演
│ b5_coloring.py M着色
│ b6_hamiltonian_cycle.py 哈密顿回路
│ b7_sudoku.py 数独
│ b8_minimax.py 极小极大
│ Python中的排列组合.md
│ _init_.py
│ [回溯Tracebacking.md](


 浙公网安备 33010602011771号
浙公网安备 33010602011771号