1.2.1 查找算法
1.2.1 查找算法[1]
简介
查找(Searching): 就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素。
查找表(Search Table):由同一类型的数据元素构成的集合
关键字(Key):数据元素中某个数据项的值,又称为键值
主键(Primary Key):可唯一的标识某个数据元素或记录的关键字
查找表按照操作方式可分为:
1.静态查找表(Static Search Table):只做查找操作的查找表。它的主要操作是:
①查询某个“特定的”数据元素是否在表中
②检索某个“特定的”数据元素和各种属性
2.动态查找表(Dynamic Search Table):在查找中同时进行插入或删除等操作:
①查找时插入数据
②查找时删除数据
顺序查找
算法简介
顺序查找又称为线性查找,是一种最简单的查找方法。适用于线性表的顺序存储结构和链式存储结构。该算法的时间复杂度为O(n)。
**基本思路 **
从第一个元素m开始逐个与需要查找的元素x进行比较,当比较到元素值相同(即m=x)时返回元素m的下标,如果比较到最后都没有找到,则返回-1。
优缺点
缺点:是当n 很大时,平均查找长度较大,效率低;
优点:是对表中数据元素的存储没有要求。另外,对于线性链表,只能进行顺序查找。 算法实现
算法实现
# 最基础的遍历无序列表的查找算法# 时间复杂度O(n)
def sequential_search(lis, key):
length = len(lis)
for i in range(length):
if lis[i] == key:
return i
else:
return False
if __name__ == '__main__':
LIST = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222]
result = sequential_search(LIST, 123)
print(result)
二分查找(Binary Search)
算法简介
二分查找(Binary Search),是一种在有序数组中查找某一特定元素的查找算法。
查找过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则查找过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。 这种查找算法每一次比较都使查找范围缩小一半。
算法描述
给予一个包含 个带值元素的数组A
1、 令 L为0 , R为 n-1
2、 如果L>R,则搜索以失败告终
3、 令 m (中间值元素)为 ⌊(L+R)/2⌋
4、 如果 Am<T,令 L为 m + 1 并回到步骤二
5、 如果 Am>T,令 R为 m - 1 并回到步骤二
复杂度分析
时间复杂度:折半搜索每次把搜索区域减少一半,时间复杂度为 O(logn) 空间复杂度:O(1) 算法实现
算法实现
# 针对有序查找表的二分查找算法
def binary_search(lis, key):
low = 0
high = len(lis) - 1
time = 0
while low < high:
time += 1
mid = int((low + high) / 2)
if key < lis[mid]:
high = mid - 1
elif key > lis[mid]:
low = mid + 1
else:
# 打印折半的次数
print("times: %s" % time)
return mid
print("times: %s" % time)
return False
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
result = binary_search(LIST, 99)
print(result)
插值查找(Interpolation Search)
算法简介
插值查找是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的 查找方法,其核心就在于插值的计算公式 (key-a[low])/(a[high]-a[low])*(high-low)。 时间复杂度o(logn)但对于表长较大而关键字分布比较均匀的查找表来说,效率较高。
算法思想
基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找。
注:对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
**复杂度分析 **
时间复杂性:如果元素均匀分布,则O(log log n),在最坏的情况下可能需要O(n)。空间复杂度:O(1)。
算法实现
# 插值查找算法
def binary_search(lis, key):
low = 0
high = len(lis) - 1
time = 0
while low < high:
time += 1
# 计算mid值是插值算法的核心代码
mid = low + int((high - low) * (key - lis[low])/(lis[high] - lis[low]))
print("mid=%s, low=%s, high=%s" % (mid, low, high))
if key < lis[mid]:
high = mid - 1
elif key > lis[mid]:
low = mid + 1
else:
# 打印查找的次数
print("times: %s" % time)
return mid
print("times: %s" % time)
return False
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
result = binary_search(LIST, 444)
print(result)
斐波那契查找(fibonacci search)
**算法简介 **
斐波那契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、····,在数学上,斐波那契被递归方法如下定义:F(1)=1,F(2)=1,F(n)=f(n-1)+F(n-2) (n>=2)。该数列越往后相邻的两个数的比值越趋向于黄金比例值(0.618)。
**算法描述 **
斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n],将原查找表扩展为长度为Fn,完成后进行斐波那契分割,即F[n]个元素分割为前半部分F[n-1]个元素,后半部分F[n-2]个元素,找出要查找的元素在那一部分并递归,直到找到。
**复杂度分析 **
最坏情况下,时间复杂度为O(logn),且其期望复杂度也为O(logn)。
算法实现
# 斐波那契查找算法
# 时间复杂度O(log(n))
def fibonacci_search(lis, key):
# 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值。
F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
233, 377, 610, 987, 1597, 2584, 4181, 6765,
10946, 17711, 28657, 46368]
low = 0
high = len(lis) - 1
# 为了使得查找表满足斐波那契特性,在表的最后添加几个同样的值
# 这个值是原查找表的最后那个元素的值
# 添加的个数由F[k]-1-high决定
k = 0
while high > F[k]-1:
k += 1
print(k)
i = high
while F[k]-1 > i:
lis.append(lis[high])
i += 1
print(lis)
# 算法主逻辑。time用于展示循环的次数。
time = 0
while low <= high:
time += 1
# 为了防止F列表下标溢出,设置if和else
if k < 2:
mid = low
else:
mid = low + F[k-1]-1
print("low=%s, mid=%s, high=%s" % (low, mid, high))
if key < lis[mid]:
high = mid - 1
k -= 1
elif key > lis[mid]:
low = mid + 1
k -= 2
else:
if mid <= high:
# 打印查找的次数
print("times: %s" % time)
return mid
else:
print("times: %s" % time)
return high
print("times: %s" % time)
return False
if __name__ == '__main__':
LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
result = fibonacci_search(LIST, 444)
print(result)
树表查找
1. 二叉树查找
**算法简介 **
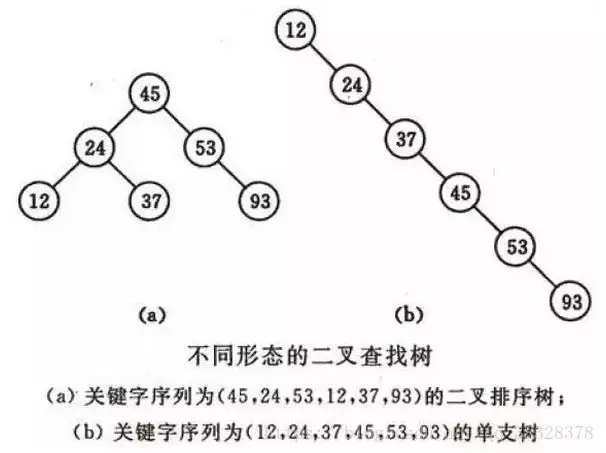
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
**算法思想 **
二叉查找树(BinarySearch Tree)或者是一棵空树,或者是具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3)任意节点的左、右子树也分别为二叉查找树。 二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
**复杂度分析 **
它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
算法实现
# 二叉树查找 Python实现
class BSTNode:
"""
定义一个二叉树节点类。
以讨论算法为主,忽略了一些诸如对数据类型进行判断的问题。
"""
def __init__(self, data, left=None, right=None):
"""
初始化
:param data: 节点储存的数据
:param left: 节点左子树
:param right: 节点右子树
"""
self.data = data
self.left = left
self.right = right
class BinarySortTree:
"""
基于BSTNode类的二叉查找树。维护一个根节点的指针。
"""
def __init__(self):
self._root = None
def is_empty(self):
return self._root is None
def search(self, key):
"""
关键码检索
:param key: 关键码
:return: 查询节点或None
"""
bt = self._root
while bt:
entry = bt.data
if key < entry:
bt = bt.left
elif key > entry:
bt = bt.right
else:
return entry
return None
def insert(self, key):
"""
插入操作
:param key:关键码
:return: 布尔值
"""
bt = self._root
if not bt:
self._root = BSTNode(key)
return
while True:
entry = bt.data
if key < entry:
if bt.left is None:
bt.left = BSTNode(key)
return
bt = bt.left
elif key > entry:
if bt.right is None:
bt.right = BSTNode(key)
return
bt = bt.right
else:
bt.data = key
return
def delete(self, key):
"""
二叉查找树最复杂的方法
:param key: 关键码
:return: 布尔值
"""
p, q = None, self._root # 维持p为q的父节点,用于后面的链接操作
if not q:
print("空树!")
return
while q and q.data != key:
p = q
if key < q.data:
q = q.left
else:
q = q.right
if not q: # 当树中没有关键码key时,结束退出。
return
# 上面已将找到了要删除的节点,用q引用。而p则是q的父节点或者None(q为根节点时)。
if not q.left:
if p is None:
self._root = q.right
elif q is p.left:
p.left = q.right
else:
p.right = q.right
return
# 查找节点q的左子树的最右节点,将q的右子树链接为该节点的右子树
# 该方法可能会增大树的深度,效率并不算高。可以设计其它的方法。
r = q.left
while r.right:
r = r.right
r.right = q.right
if p is None:
self._root = q.left
elif p.left is q:
p.left = q.left
else:
p.right = q.left
def __iter__(self):
"""
实现二叉树的中序遍历算法,
展示我们创建的二叉查找树.
直接使用python内置的列表作为一个栈。
:return: data
"""
stack = []
node = self._root
while node or stack:
while node:
stack.append(node)
node = node.left
node = stack.pop()
yield node.data
node = node.right
if __name__ == '__main__':
lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
bs_tree = BinarySortTree()
for i in range(len(lis)):
bs_tree.insert(lis[i])
# bs_tree.insert(100)
bs_tree.delete(58)
for i in bs_tree:
print(i, end=" ")
# print("\n", bs_tree.search(4))
2. 平衡查找树之2-3查找树(2-3 Tree)
算法描述
2-3查找树定义
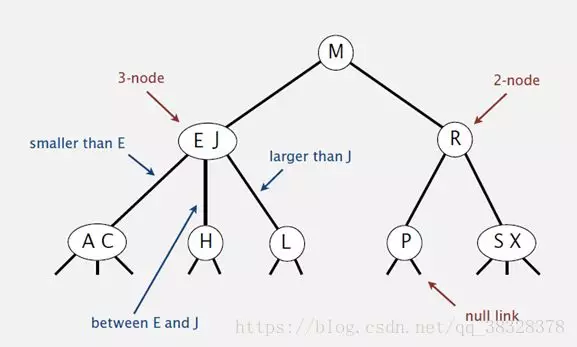
和二叉树不一样,2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node),他保存1个key和左右两个自己点。对应3节点(3-node),保存两个Key,2-3查找树的定义如下:
1)要么为空,要么:
2)对于2节点,该节点保存一个key及对应value,以及两个指向左右节点的节点,左节点也是一个2-3节点,所有的值都比key要小,右节点也是一个2-3节点,所有的值比key要大。
3)对于3节点,该节点保存两个key及对应value,以及三个指向左中右的节点。左节点也是一个2-3节点,所有的值均比两个key中的最小的key还要小;中间节点也是一个2-3节点,中间节点的key值在两个跟节点key值之间;右节点也是一个2-3节点,节点的所有key值比两个key中的最大的key还要大。
####### 2-3查找树的性质
1)如果中序遍历2-3查找树,就可以得到排好序的序列;
2)在一个完全平衡的2-3查找树中,根节点到每一个为空节点的距离都相同。(这也是平衡树中“平衡”一词的概念,根节点到叶节点的最长距离对应于查找算法的最坏情况,而平衡树中根节点到叶节点的距离都一样,最坏情况也具有对数复杂度。)
复杂度分析
2-3树的查找效率与树的高度是息息相关的。
距离来说,对于1百万个节点的2-3树,树的高度为12-20之间,对于10亿个节点的2-3树,树的高度为18-30之间。
对于插入来说,只需要常数次操作即可完成,因为他只需要修改与该节点关联的节点即可,不需要检查其他节点,所以效率和查找类似。
3. 平衡查找树之红黑树(Red-Black Tree)
**算法描述 **
**红黑树的定义 **
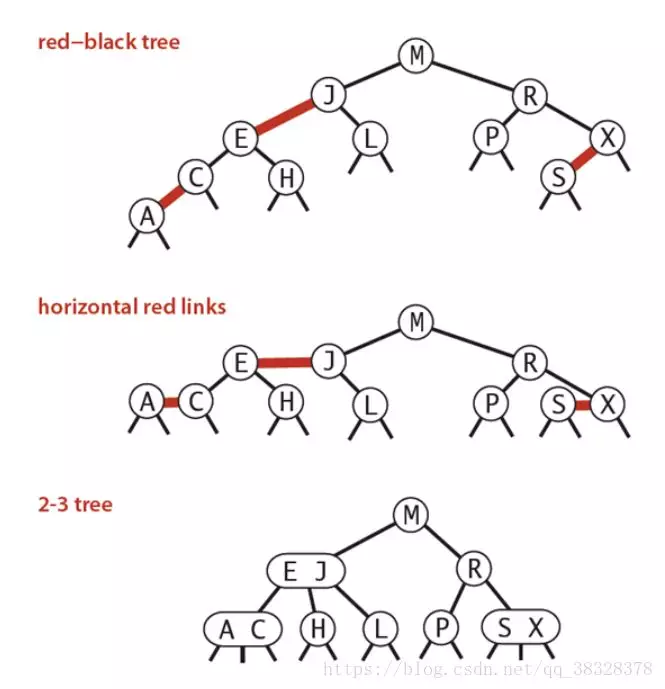
红黑树是一种具有红色和黑色链接的平衡查找树,同时满足:
① 红色节点向左倾斜 ;
②一个节点不可能有两个红色链接;
③整个树完全黑色平衡,即从根节点到所以叶子结点的路径上,黑色链接的个数都相同。
红黑树的性质
整个树完全黑色平衡,即从根节点到所以叶子结点的路径上,黑色链接的个数都相同(2-3树的第2)性质,从根节点到叶子节点的距离都相等)。
复杂度分析
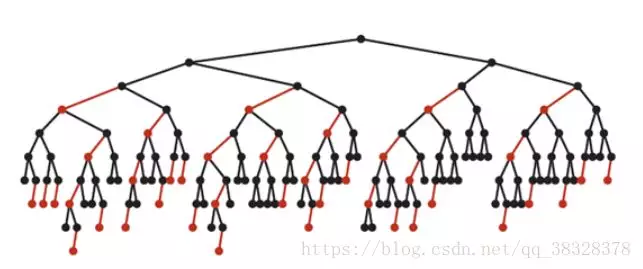
最坏的情况就是,红黑树中除了最左侧路径全部是由3-node节点组成,即红黑相间的路径长度是全黑路径长度的2倍。
下图是一个典型的红黑树,从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍:
4. B树和B+树(B Tree/B+ Tree)
**B树算法简介 **
B 树可以看作是对2-3查找树的一种扩展,即他允许每个节点有M-1个子节点。
①根节点至少有两个子节点;
②每个节点有M-1个key,并且以升序排列;
③位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间;
④非叶子结点的关键字个数=指向儿子的指针个数-1;
⑤非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] ;
⑥其它节点至少有M/2个子节点;
⑦所有叶子结点位于同一层; 如:(M=3)
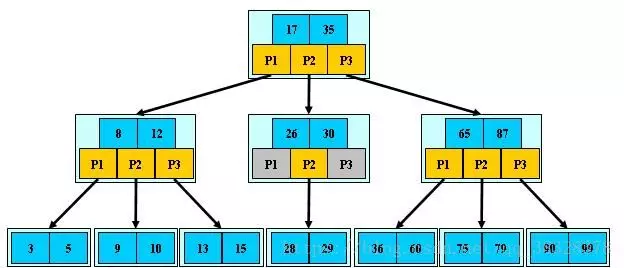
**B树算法思想 **
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
B树的特性
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少利用率,其最底搜索性能为O(LogN)
B+ 树算法简介
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
4.B-树是开区间;
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
如:(M=3)
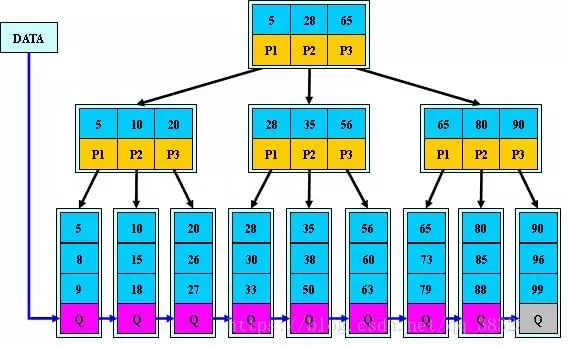
B+树算法思想
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+树的特性
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统;
5. 树表查找总结
二叉查找树平均查找性能不错,为O(logn),但是最坏情况会退化为O(n)。
在二叉查找树的基础上进行优化,我们可以使用平衡查找树。平衡查找树中的2-3查找树,这种数据结构在插入之后能够进行自平衡操作,从而保证了树的高度在一定的范围内进而能够保证最坏情况下的时间复杂度。但是2-3查找树实现起来比较困难,红黑树是2-3树的一种简单高效的实现,他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树,应用非常广泛,很多编程语言的内部实现都或多或少的采用了红黑树。
除此之外,2-3查找树的另一个扩展——B/B+平衡树,在文件系统和数据库系统中有着广泛的应用。
分块查找(Blocking Search)
**算法简介 **
分块查找又称索引顺序查找,它是顺序查找的一种改进方法。
**算法思想 **
将n个数据元素"按块有序"划分为m块(m ≤ n)。 每一块中的结点不必有序,但块与块之间必须"按块有序"; 即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字; 而第2块中任一元素又都必须小于第3块中的任一元素,……
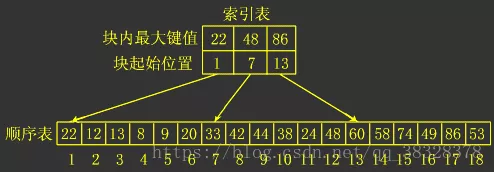
算法流程
- 先选取各块中的最大关键字构成一个索引表;
- 查找分两个部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;
- 在已确定的块中用顺序法进行查找。 复杂度分析
时间复杂度
O(log(m)+N/m)
哈希查找(Hash Search)
算法简介
哈希表就是一种以键-值(key-indexed) 存储数据的结构,只要输入待查找的值即key,即可查找到其对应的值。
**算法思想 **
哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
算法流程
- 用给定的哈希函数构造哈希表;
- 根据选择的冲突处理方法解决地址冲突;常见的解决冲突的方法:拉链法和线性探测法。
- 在哈希表的基础上执行哈希查找。
复杂度分析
单纯论查找复杂度:对于无冲突的Hash表而言,查找复杂度为O(1)(注意,在查找之前我们需要构建相应的Hash表)。
算法实现
# 忽略了对数据类型,元素溢出等问题的判断。
class HashTable:
def __init__(self, size):
self.elem = [None for i in range(size)] # 使用list数据结构作为哈希表元素保存方法
self.count = size # 最大表长
def hash(self, key):
return key % self.count # 散列函数采用除留余数法
def insert_hash(self, key):
"""插入关键字到哈希表内"""
address = self.hash(key) # 求散列地址
while self.elem[address]: # 当前位置已经有数据了,发生冲突。
address = (address+1) % self.count # 线性探测下一地址是否可用
self.elem[address] = key # 没有冲突则直接保存。
def search_hash(self, key):
"""查找关键字,返回布尔值"""
star = address = self.hash(key)
while self.elem[address] != key:
address = (address + 1) % self.count
if not self.elem[address] or address == star: # 说明没找到或者循环到了开始的位置
return False
return True
if __name__ == '__main__':
list_a = [12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34]
hash_table = HashTable(12)
for i in list_a:
hash_table.insert_hash(i)
for i in hash_table.elem:
if i:
print((i, hash_table.elem.index(i)), end=" ")
print("\n")
print(hash_table.search_hash(15))
print(hash_table.search_hash(33))
散列表查找性能分析
如果没发生冲突,则其查找时间复杂度为O(1),属于最极端的好了。
但是,现实中冲突可不可避免的,下面三个方面对查找性能影响较大:
- 散列函数是否均匀
- 处理冲突的办法
- 散列表的装填因子(表内数据装满的程度)
六种查找算法的时间复杂度
- 顺序查找算法:按照数据的顺序一项一项逐个查找,所以不管数据顺序如何,都要从头到尾的遍历一次。速度比较慢,它的时间复杂度是 T=O(n)。
- 二分查找算法:将数据分割成两等份,然后用键值(要查找的数据)与中间值比较,逐渐缩短查找范围。速度比顺序查找快,它的时间复杂度是 T=O(log n)。
- 插补查找算法:按照数据的分布,利用公式预测键值所在的位置,快速缩小键值所在序列的范围,慢慢逼近,直到查找到数据为止,这种算法比二分查找速度还快,它的时间复杂度是 T=O(log log(n))。
- 分块查找算法:要求是顺序表,它是顺序查找的一种改进方法,它的时间复杂度是 T= O(log2(m)+N/m)。
- 斐波那契查找算法:斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。用键值(要查找的数据)与黄金分割点进行比较,逐渐缩短查找范围。它的时间复杂度是 T=O(log 2n)。
- 哈希查找算法:把一些复杂的数据,通过某种函数映射(概念和数学中映射一样)关系,映射成更加易于查找的方式。这种方法速度最快,它的时间复杂度是 T=O(1)。
六种查找算法的时间复杂度如下表所示:
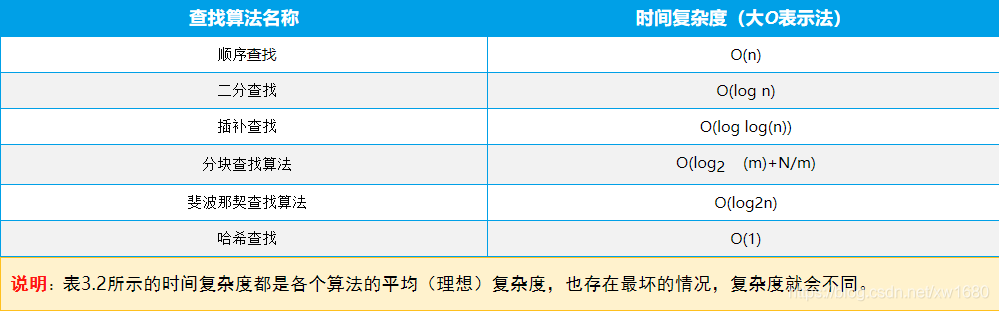
线性索引查找
对于海量的无序数据,为了提高查找速度,一般会为其构造索引表。
索引就是把一个关键字与它相对应的记录进行关联的过程。
一个索引由若干个索引项构成,每个索引项至少包含关键字和其对应的记录在存储器中的位置等信息。
索引按照结构可以分为:线性索引、树形索引和多级索引。
线性索引:将索引项的集合通过线性结构来组织,也叫索引表。
线性索引可分为:稠密索引、分块索引和倒排索引
稠密索引
稠密索引指的是在线性索引中,为数据集合中的每个记录都建立一个索引项。
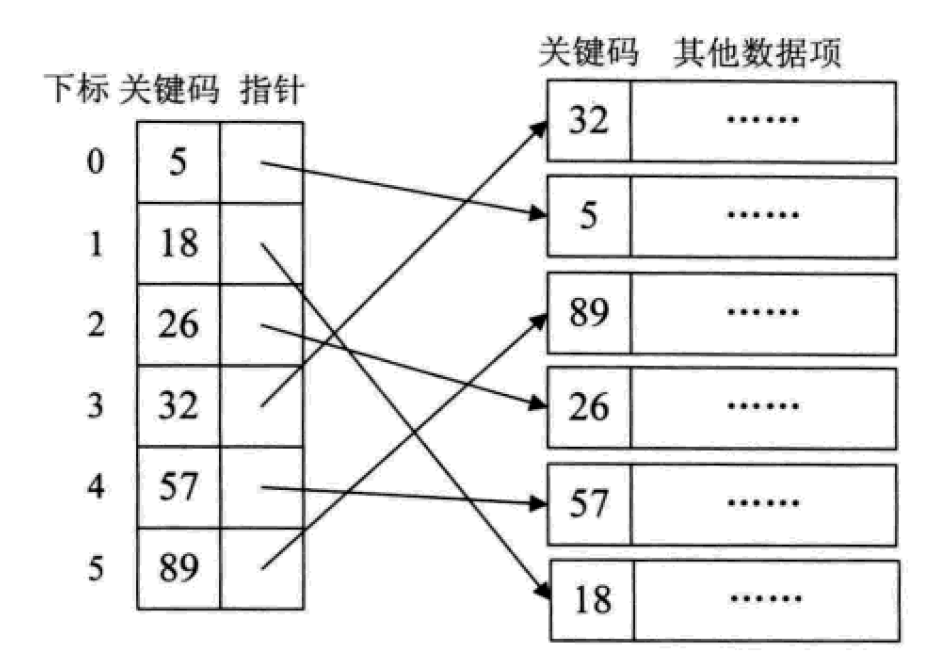
这其实就相当于给无序的集合,建立了一张有序的线性表。其索引项一定是按照关键码进行有序的排列。
这也相当于把查找过程中需要的排序工作给提前做了。
分块索引
给大量的无序数据集合进行分块处理,使得块内无序,块与块之间有序。
这其实是有序查找和无序查找的一种中间状态或者说妥协状态。因为数据量过大,建立完整的稠密索引耗时耗力,占用资源过多;但如果不做任何排序或者索引,那么遍历的查找也无法接受,只能折中,做一定程度的排序或索引。
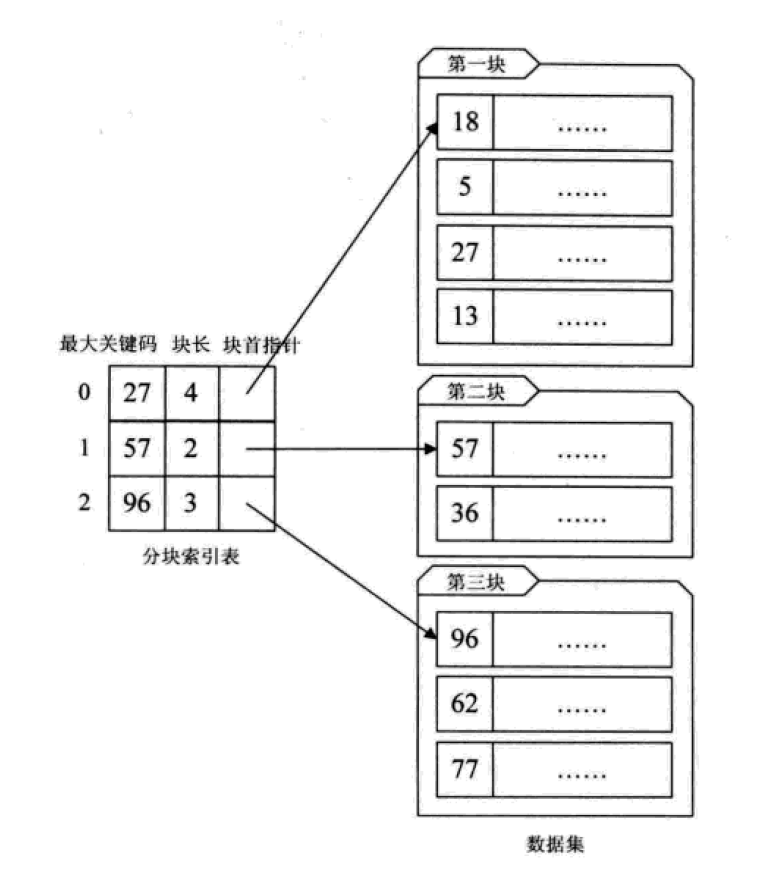
分块索引的效率比遍历查找的O(n)要高一些,但与二分查找的O(logn)还是要差不少。
倒排索引
不是由记录来确定属性值,而是由属性值来确定记录的位置,这种被称为倒排索引。其中记录号表存储具有相同次关键字的所有记录的地址或引用(可以是指向记录的指针或该记录的主关键字)。
倒排索引是最基础的搜索引擎索引技术。
爬山算法(hill climbing)
简介爬山算法是一种局部择优的方法,采用启发式方法,是对深度优先搜索的一种改进,它利用反馈信息帮助生成解的决策。 属于人工智能算法的一种。
算法解释:
从当前的节点开始,和周围的邻居节点的值进行比较。 如果当前节点是最大的,那么返回当前节点,作为最大值(既山峰最高点);反之就用最高的邻居节点来,替换当前节点,从而实现向山峰的高处攀爬的目的。如此循环直到达到最高点。
算法优缺点
优点
避免遍历,通过启发选择部分节点,从而达到提高效率的目的。
缺点
因为不是全面搜索,所以结果可能不是最佳。
爬山算法一般存在以下问题:
1)、局部最大:某个节点比周围任何一个邻居都高,但是它却不是整个问题的最高点。
2)、高地:也称为平顶,搜索一旦到达高地,就无法确定搜索最佳方向,会产生随机走动,使得搜索效率降低。
3)、山脊:搜索可能会在山脊的两面来回震荡,前进步伐很小。
模拟退火算法(Simulated Annealing Algorithm)
模拟退火其实也是一种贪心算法,只不过与Local Search不同的是,模拟退火算法在搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。
根据热力学的原理,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:
P(dE) = exp( dE/(kT) )
其中k是一个常数,exp表示自然指数,且dE<0(温度总是降低的)。
算法描述
- 初始化:初始温度T(充分大),温度下限Tmin(充分小),初始解状态x(是算法迭代的起点),每个T值的迭代次数L;
- 对l=1,2,...,L做第3至第6步;
- 产生新解x_new: (x_new=x+Δx);
- 利计算增量Δf=f(x_new)−f(x),其中f(x)为优化目标;
- 若Δf<0(若寻找最大值,Δf>0)则接受x_new作为新的当前解,否则以概率exp(−Δf/(kT))接受x_new作为新的当前解;
- 如果满足终止条件则输出当前解作为最优解,结束程序。(终止条件通常取为连续若干个新解都没有被接受时终止算法。);
- T逐渐减少,且T>Tmin,然后转第2步。
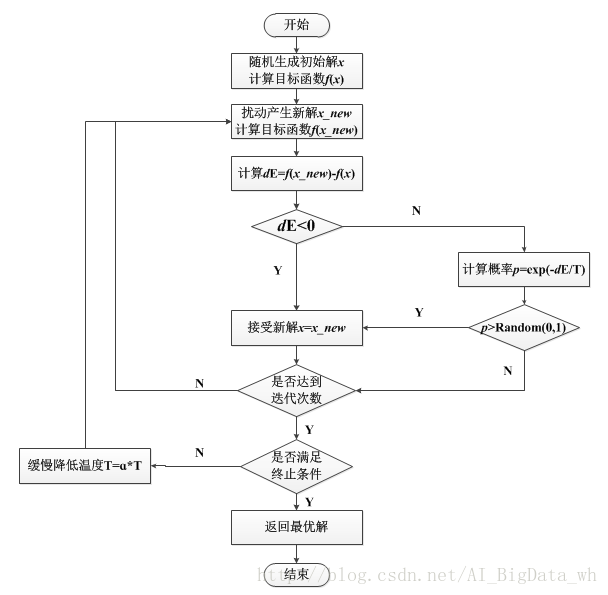
算法的优缺点
模拟退火算法的应用很广泛,可以高效地求解NP完全问题,如货郎担问题(Travelling Salesman Problem,简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等,但其参数难以控制,不能保证一次就收敛到最优值,一般需要多次尝试才能获得(大部分情况下还是会陷入局部最优值)。观察模拟退火算法的过程,发现其主要存在如下三个参数问题:
(1) 温度T的初始值设置问题
温度TT的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间;反之,则可节约计算时间,但全局搜索性能可能受到影响。
(2) 退火速度问题,即每个TT值的迭代次数
模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说,同一温度下的“充分”搜索是相当必要的,但这也需要计算时间。循环次数增加必定带来计算开销的增大。
(3) 温度管理问题
温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中,由于必须考虑计算复杂度的切实可行性等问题,常采用如下所示的降温方式:
T=α×T.α∈(0,1).
注:为了保证较大的搜索空间,α一般取接近于1的值,如0.95、0.9。
跳跃搜索算法(Jump Search )
跳跃搜索算法跟二分查找算法类似,它也是针对有序序列的查找,只是它是通过查找比较少的元素找到目标。当然它需要通过固定的跳跃间隔,这样它相比二分查找效率提高了很多。
假设我们有一个大小为n的数组arr []和要跳跃的大小m。 然后我们搜索索引arr [0],arr [m],arr [2m] ... ..arr [km]等等。 一旦我们找到间隔(arr [km] <x <arr [(k + 1)m]),我们从索引km执行线性搜索操作来找到元素x。
我们考虑以下数组:(0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610)。 数组的长度为16。跳跃搜索将以下列步骤找到值55,假设要跳过的大小为4。
步骤1:从索引0跳转到索引4;
步骤2:从索引4跳转到索引8;
步骤3:从索引8跳转到索引16;
步骤4:由于索引16处的元素大于55,因此我们将跳回一步到索引9。
步骤5:从索引9执行线性搜索以获得元素55。
算法小结:
时间复杂度:O(√n)
辅助空间:O(1)
一、该算法仅适用于有序数组
二、要跳转的最佳大小为O(√n), 这使得跳跃搜索O(√n)的时间复杂度。
三、跳跃搜索的时间复杂度在线性搜索((O(n))和二分查找搜索(O(Log n))之间。
四、二分查找算法相比跳跃搜索更好,但是跳跃搜索有以下优点:跳跃搜索仅遍历一次,而二分查找最多需要O(Log n),考虑要搜索的元素是最小元素或小于 最小的),我们选用Jump Search。
快速选择算法(Quick select)
Quick select算法通常用来在未排序的数组中寻找第k小/第k大的元素。其方法类似于Quick sort。Quick select和Quick sort都是由Tony Hoare发明的,因此Quick select算法也被称为是Hoare's selection algorithm。Quick select算法因其高效和良好的average case时间复杂度而被广为应用。Quick select的average case时间复杂度为O(n),然而其worst case时间复杂度为O(n^2)。- 总体而言,
Quick select采用和Quick sort类似的步骤。首先选定一个pivot,然后根据每个数字与该pivot的大小关系将整个数组分为两部分。那么与Quick sort不同的是,Quick select只考虑所寻找的目标所在的那一部分子数组,而非像Quick sort一样分别再对两边进行分割。正是因为如此,Quick select将平均时间复杂度从O(nlogn)降到了O(n)。
算法描述
Input: array nums, int k. (find kth smallest element in an unsorted array)
Output: int target
- Choose an element from the array as pivot, exchange the position of pivot and number at the end of the array.
- _The pivot can either be the end element or a random chosen element. A random chosen pivot can make the algorithm much possibly run in average case time. _
- Partition the array into 2 parts in which the numbers in left subarray is less than (or equal to) the pivot and the numbers in right subarray is greater than (or equal to) the pivot.
- Exchange pivot (at the end of the array now) with the first element in the right part.
- Compare k with length of the left subarray, say, len.
- if k == len + 1, then pivot is the target.
- if k <= len, repeat from step 1 on the left subarray.
- if k > len, k = k - len, repeat from step 1 on the right subarray.
禁忌搜索算法(Tabu Search)
概念
禁忌搜索(Tabu Search或Taboo Search,简称TS)是对局部搜索(LS)的一种扩展。所谓禁忌,就是禁止重复前面的操作。为了改进局部邻域搜索容易陷入局部最优点的不足,禁忌搜索算法引入一个禁忌表,记录下已经搜索过的局部最优点,在下一次搜索中,对禁忌表中的信息不再搜索或有选择地搜索,以此来跳出局部最优点,从而最终实现全局优化。禁忌搜索算法是对局部邻域搜索的一种扩展,是一种全局邻域搜索、逐步寻优的算法。
思路

相关术语
禁忌表(Tabu List,TL)
是用来存放(记忆)禁忌对象的表。它是禁忌搜索得以进行的基本前提。禁忌表本身是有容量限制的,它的大小对存放禁忌对象的个数有影响,会影响算法的性能。
禁忌对象(Tabu Object,TO)
是指禁忌表中被禁的那些变化元素。禁忌对象的选择可以根据具体问题而制定。例如在旅行商问题(Traveling Salesman Problem,TSP)中可以将交换的城市对作为禁忌对象,也可以将总路径长度作为禁忌对象。
禁忌期限(Tabu Tenure,TT)
也叫禁忌长度,指的是禁忌对象不能被选取的周期。禁忌期限过短容易出现循环,跳不出局部最优,长度过长会造成计算时间过长。
渴望准则(Aspiration Criteria,AC)
也称为特赦规则。当所有的对象都被禁忌之后,可以让其中性能最好的被禁忌对象解禁,或者当某个对象解禁会带来目标值的很大改进时,也可以使用特赦规则。
停止规则:禁忌搜索中停止规则的设计多种多样,如最大迭代数、算法运行时间、给定数目的迭代内不能改进解或组合策略等等。
对于优化问题相关算法有如下分类:
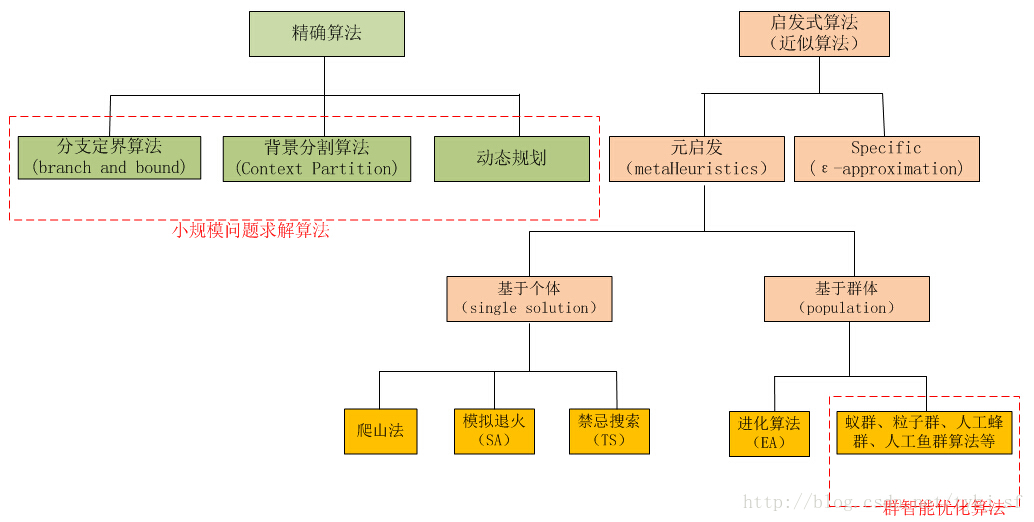
三分搜索树(Ternary Tree)
基本概念:
有三个只节点,在查找的时候,比较当前字符,如果查找的字符比较小,那么就跳到左节点.如果查找的字符比较大,那么就跳转到右节点.如果这个字符正好相等,那么就走向中间节点.这个时候比较下一个字符。
举例说明:
比如要查找”ax”:
先比较”a” 和 “i”, “a” < “i”,跳转到”i”的左节点;
比较 “a” < “b”, 跳转到”b”的左节点;
比较”a” = “a”,跳转到 “a”的中间节点,并且比较下一个字符”x”;
比较”x” > “s” , 跳转到”s” 的右节点;
比较 “x” > “t” 发现”t” 没有右节点了;
找出结果,不存在”ax”这个字符;
插入
字符串作为 key,插入 key 的时候,从树根作为当前节点开始(树为空的时候树根为 nil),一个字符一个字符的递归执行下面过程。
- 如果当前节点为 nil,则创建一个新的节点,将当前字符保存在节点中,将其设置为当前节点。
- 如果当前字符和当前节点保存的字符都为 ‘/0′,将数据存于当前节点,终止调用。
- 如果当前字符小于当前节点保存的字符,那么递归将当前字符 插入节点的 left 子节点,大于则插入 right 子节点;相等则将下一个字符 插入当前节点的 mid 子节点。
查找
查找的过程和插入类似,把 key 一个字符一个字符的和树中节点保存的字符进行比较,同样从树根开始递归执行。
- 如果当前节点为 nil,则查找失败。
- 如果当前字符比节点中的小,递归对 left 子节点查找,依然比较当前字符。
- 如果当前字符比节点中的大,递归对 right 子节点查找,依然比较当前字符。
- 如果当前字符与节点中的相等且都为 ‘/0′,则这个节点中就存着 key 对应的 value,终止调用。如果相等但是不是 ‘/0′,则递归对 mid 子节点查找,比较字符为下一个字符。
│ s1_linear_search.py 顺序查找
│ s1_double_linear_search.py 双向顺序查找
│ s1_double_linear_search_recursion.py 双向顺序查找递归
│ s1_sentinel_linear_search.py 哨兵顺序查找
│ s2_binary_search.py 二分查找
│ s2_simple_binary_search.py 二分查找
│ s3_interpolation_search.py 插值查找
│ s4_binary_tree_traversal.py 二叉树查找
│ s5_fibonacci_search.py 斐波那契查找
│ s6_quick_select.py 快速选择查找
│ s7_jump_search.py 跳跃查找
│ s8_hill_climbing.py 爬山查找
│ s9_simulated_annealing.py 模拟退火查找
│ s10_tabu_search.py 禁忌查找
│ s11_ternary_search.py 三分查找
│ __init__.py
│ 查找算法Search.md 学习笔记
Reference
https://mp.weixin.qq.com/s/goi5MCojtUp_CPiOJI9Ejg 《七大查找算法(Python)》 ↩︎



