1.1.9 图Graph
1.1.9 图(Graph)
图是数据结构和算法学中最强大的框架之一(或许没有之一)。图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。
图的定义:
一个图是一个二元组(V,E),其中:
1)V是一个非空有穷的顶点集合
2)E是顶点偶对(称为边)的集合
3)V中的顶点也称为图G的顶点,E中的边也称为图G的边
基本属性:
1)图分为有向图和无向图两种,有向图的边有方向,是顶点的有序对;无向图中的边没有方向,是顶点的无序对
2)一个顶点的度就是与它邻接的边的条数,对于有向图,顶点的度还分为入度和出度,分别表示以该顶点为终点或者始点的边的条数
3)如果在有向图G里存在一个顶点v,从顶点v到图G中其他每个顶点均有路径,则称G为有根图,称顶点v为图G的一个根
4)连通无向图:如果无向图G中任意两个顶点vi与vj之间都连通,则称G为连通无向图;强连通有向图:如果对有向图G中任意两个顶点vi和vj,从vi到vj以及从vj到vi都有路径,则称G为强连通有向图
5)如果图G中的每条边都被赋予一个权值,则称G为一个带权图。边的权值可用于表示实际应用中与顶点之间的关联有关的某些信息。带权的连通无向图也被称为网络
术语表:
- 顶点 Vertex(也“节点node”)
是图的基本组成部分,定点具有名称标识key,也可以携带数据项payload。 - 边 Edge(也称“弧Arc”)
作为2个顶点之间关系的表示,边连接两个顶点;边可以是有向的或者无向的,相应的图称做“有向图”和“无向图”。 - 权重 Weight
为了表达从一个顶点到另一个顶点的“代价”,可以给边赋权;例如公交网络中两个站点之间的“距离”、“通行时间”和“票价”都可以作为权重。 - 路径Path
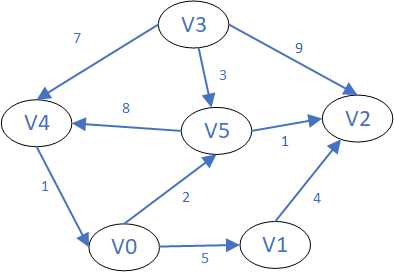
图中的路径,是由边依次链接起来的顶点序列;无权路径的长度为边的数量;带权路径的长度为所有边权重的和;如下图的一条路径(v3,v4,v0,v1) - 圈Cycle
圈是首尾顶点相同的路径,如下图中(V5,V2,V3,V5)
如果有向图中不存在任何圈,则称为“有向无圈图 directed acyclic graph:DAG”
如果一个问题能表示成DAG,就可以用图算法很好地解决。
抽象数据类型:ADT Graph[1]
定义
Graph() 创建一个空图
addVertex(vert) 将顶点vert加入图中
addEdge(fromVert, toVert) 添加有向边
addEdge(fromVert, toVert, weight) 添加带权的有向边
getVertex(vKey) 查找名称为vKey的顶点
getVertices() 返回图中所有顶点列表
in 按照vert in graph的语句形式,返回顶点是否存在图中True/False
ADT Graph的实现方法
两种方法各有优劣,需要在不同应用中加以选择
-
邻接矩阵adjacency matrix
-
邻接表adjacency list
邻接矩阵Adjacency Matrix
矩阵的每行和每列都代表图中的顶点,如果两个顶点之间有边相连,设定行列值
-
无权边则将矩阵分量标注为1,或者0
-
带权边则将权重保存为矩阵分量值
例如下面的带权图:

邻接矩阵顶实现法的优点是简单,可以很容易得到顶点是如何相连
但如果图中的边数很少则效率低下,成为“稀疏sparse”矩阵,而大多数问题所对应的图都是稀疏的,边远远少于|V|2这个量级,从而出现邻接列表。
算法实现:
inf = float('inf') #定义一个无穷大的量表示无边情况
#采用邻接矩阵实现
class Graph:
def __init__(self,mat,unconn = 0): #初始化
vnum = len(mat)
for x in mat:
if len(x) != vnum:
raise ValueError("Argument for 'Graph'.")
self._mat = [mat[i][:] for i in range(vnum)] #使用拷贝的数据
self._unonn = unconn
self._vnum = vnum
def vertex_num(self): #返回结点数目
return self._vnum
def _invalid(self,v): #检验输入的结点是否合法
return v > 0 or v >= self._vnum
def add_adge(self,vi,vj,val=1): #增加边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + 'is not a valid vertex.')
self._mat[vi][vj] = val
def get_adge(self,vi,vj): #得到边的信息
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + 'is not a valid vertex.')
return self._mat[vi][vj]
def out_edges(self,vi): #得到vi出发的所有边
if self._invalid(vi):
raise GraphError(str(vi)+' is not a valid vertex.')
return self._out_edges(self._mat[vi],self._unconn)
@staticmethod
def _out_edges(row,unconn): #辅助函数
edges = []
for i in range(len(row)):
if row[i] != unconn:
edges.append((i,row[i]))
return edges
def __str__(self): #输出的str方法
return '[\n' + ',\n'.join(map(str,self._mat)) + '\n]' + '\nUnconnected: ' + str(self._unconn)
邻接列表Adjacency List
-
邻接列表可以成为稀疏图的更高效实现方案
维护一个包含所有顶点的主列表(master list)。主列表中的每个顶点,再关联一个与自身由边链接的所有顶点的列表。 -
邻接列表法的寻出空间紧凑高效
很容易获得顶点所连接的所有顶点以及边的信息
例如上面的图转为邻接列表,与V0有关的有V1和V5,权重分别是5和2:
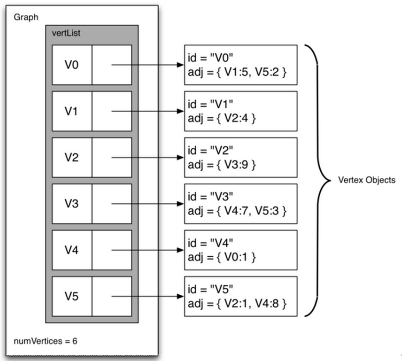
算法实现:
#采用邻接表实现,需要重写一些方法,但功能相同
class GraphAL(Graph): #继承于Graph
def __init__(self,mat=[],unconn=0):
vnum = len(mat)
for x in mat:
if len(x) !=vnum:
raise ValueError("Argument for 'Graph'.")
self._mat = [Graph._out_edges(mat[i],unconn) for i in range(vnum)]
self._vnum = vnum
self._unconn = unconn
def add_edge(self,vi,vj,val = 1):
if self._vnum == 0:
raise GraphError('Cannot add edge to empty graph.')
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + ' is not valid vertex.')
row = self._mat[vi]
i = 0
while i < len(row):
if row[i][0] == vj:
self._mat[vi][i] = (vj,val)
return
if row[i][0] > vj:
break
i += 1
self._mat[vi].insert(i,(vj,val))
def get_edge(self,vi,vj):
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + ' or' + str(vj) + ' is not valid vertex.')
for i,val in self._mat[vi]:
if i == vj:
return val
return self._unconn
def out_edges(self,vi):
if self._invalid(vi):
raise GraphError(str(vi) + ' is not valid vertex.')
return self._mat[vi]
ADT Graph的代码实现
Vertex类
下面展示了 Vertex 类的代码,包含了顶点信息, 以及顶点连接边信息
算法实现:
class Vertex:
def __init__(self,key):
self.id = key
self.connectedTo = {}
#从这个顶点添加一个连接到另一个
def addNeighbor(self,nbr,weight=0): #nbr是顶点对象的key
self.connectedTo[nbr] = weight
#顶点数据字符串化,方便打印
def __str__(self):
return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
#返回邻接表中的所有顶点
def getConnections(self):
return self.connectedTo.keys()
#返回key
def getId(self):
return self.id
#返回顶点边的权重。
def getWeight(self,nbr):
return self.connectedTo[nbr]
Graph 类
Graph 类的代码,包含将顶点名称映射到顶点对象的字典。
Graph 还提供了将顶点添加到图并将一个顶点连接到另一个顶点的方法。
getVertices方法返回图中所有顶点的名称。
此外,我们实现了iter 方法,以便轻松地遍历特定图中的所有顶点对象。 这两种方法允许通过名称或对象本身在图形中的顶点上进行迭代。
算法实现:
class Graph:
def __init__(self):
self.vertList = {}
self.numVertices = 0
#新加顶点
def addVertex(self,key):
self.numVertices = self.numVertices + 1
newVertex = Vertex(key)
self.vertList[key] = newVertex
return newVertex
#通过key查找顶点
def getVertex(self,n):
if n in self.vertList:
return self.vertList[n]
else:
return None
def __contains__(self,n):
return n in self.vertList
def addEdge(self,f,t,cost=0):
if f not in self.vertList: #不存在的顶点先添加
nv = self.addVertex(f)
if t not in self.vertList:
nv = self.addVertex(t)
self.vertList[f].addNeighbor(self.vertList[t], cost)
def getVertices(self):
return self.vertList.keys()
def __iter__(self):
return iter(self.vertList.values())
图的搜索
回溯法(探索与回溯法)是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
深度优先搜索(DFS)
深度优先搜索(Depth_Fisrst Search)遍历类似于树的先根遍历,是树的先根遍历的推广。
深度优先搜索实现步骤:
(1)访问初始顶点v并标记顶点v已访问。
(2)查找顶点v的第一个邻接顶点w。
(3)若顶点v的邻接顶点w存在,则继续执行;否则回溯到v,再找v的另外一个未访问过的邻接点。
(4)若顶点w尚未被访问,则访问顶点w并标记顶点w为已访问。
(5)继续查找顶点w的下一个邻接顶点wi,如果v取值wi转到步骤(3)。直到连通图中所有顶点全部访问过为止
假设初始状态是图中所有顶点未曾被访问,则深度优先搜索可从图中某个顶点发v 出发,访问此顶点,然后依次从v 的未被访问的邻接点出发深度优先遍历图,直至图中所有和v 有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
以如下图的无向图G5为例,进行图的深度优先搜索:
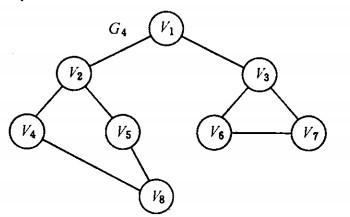
深度优先搜索过程:
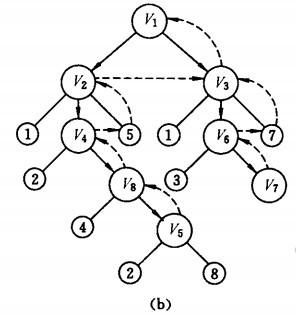
假设从顶点v1 出发进行搜索,在访问了顶点v1 之后,选择邻接点v2。因为v2 未曾访问,则从v2 出发进行搜索。依次类推,接着从v4 、v8 、v5 出发进行搜索。在访问了v5 之后,由于v5 的邻接点都已被访问,则搜索回到v8。由于同样的理由,搜索继续回到v4,v2 直至v1,此时由于v1 的另一个邻接点未被访问,则搜索又从v1 到v3,再继续进行下去由此,得到的顶点访问序列为:

显然,这是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问,需附设访问标志数组visited[0:n-1], ,其初值为FALSE ,一旦某个顶点被访问,则其相应的分量置为TRUE。
算法实现:
from pythonds.graphs import Graph
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)
广度优先搜索(BFS)
广度优先搜索(Breadth_First Search) 遍历类似于树的按层次遍历的过程。
广度优先实现步骤:
(1)顶点v入队列。
(2)当队列非空时则继续执行,否则算法结束。
(3)出队列取得队头顶点v;访问顶点v并标记顶点v已被访问。
(4)查找顶点v的第一个邻接顶点col。
(5)若v的邻接顶点col未被访问过的,则col入队列。
(6)继续查找顶点v的另一个新的邻接顶点col,转到步骤(5)。直到顶点v的所有未被访问过的邻接点处理完。转到步骤(2)。
假设从图中某顶点v 出发,在访问了v 之后依次访问v 的各个未曾访问过和邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程中以v 为起始点,由近至远,依次访问和v 有路径相通且路径长度为1,2,…的顶点。
对图如下图所示无向图G5 进行广度优先搜索遍历:

广度优先搜索过程:
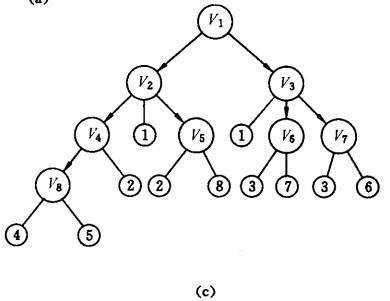
首先访问v1 和v1 的邻接点v2 和v3,然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7,最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问,并且图中所有顶点都被访问,由些完成了图的遍历。得到的顶点访问序列为:
v1→v2 →v3 →v4→ v5→ v6→ v7 →v8
和深度优先搜索类似,在遍历的过程中也需要一个访问标志数组。并且,为了顺次访问路径长度为2、3、…的顶点,需附设队列以存储已被访问的路径长度为1、2、… 的顶点。
算法实现:
from pythonds.graphs import Graph, Vertex
from pythonds.basic import Queue
def bfs(g,start):
start.setDistance(0)
start.setPred(None)
vertQueue = Queue()
vertQueue.enqueue(start)
while (vertQueue.size() > 0):
currentVert = vertQueue.dequeue()
for nbr in currentVert.getConnections():
if (nbr.getColor() == 'white'):
nbr.setColor('gray')
nbr.setDistance(currentVert.getDistance() + 1)
nbr.setPred(currentVert)
vertQueue.enqueue(nbr)
currentVert.setColor('black')
图的简单应用
图是实际中经常运用到的数据结构,这里列举出两个经典的问题,给出解决算法。[2]
最小生成树解法
假定G是一个网络,其中的边带有给定的权值,可以做出它的生成树,现将G的一棵生成树中各条边的权值之和称为该生成树的权。网络G可能存在许多棵不同的生成树,不同生成树的权值也有可能不同,其中权值最小的生成树称为G的最小生成树
Kruskal算法
Kruskal算法是一种构造最小生成树的简单算法,其中的思想也比较简单
算法思想:
(1)设G = (V,E)是一个网络,其中|V| = n。初始时取包含G中所有n个顶点但没有任何边的孤立点子图T= (V,{}),T里的每一个顶点自成一个连通分量
(2)将边集E中的边按权值递增的顺序排列,在构造中的每一步顺序地检查这个边序列,找到下一条(最短的)两端点位于T的两个不同连通分量的边e,把e加入T。这导致两个连通分量由于边e的连接而变成了一个连通分量
(3)每次操作使T减少一个连通分量,不断重复这个动作加入新边,直到T中所有顶点都包含在一个连通分量里为止,这个连通分量就是G的一棵最小生成树
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点看成独立的n棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点ui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
- 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
算法实现:
#Krudkal最小生成树算法
def Kruskal(graph):
vnum = graph.vertex_num()
reps = [i for i in range(vnum)]
mst,edges = [],[]
for vi in range(vnum): #所有边入表
for v,w in graph.out_edges(vi):
edges.append((w,vi,v))
edges.sort() #按权值排序
for w,vi,vj in edges:
if reps[vi] != reps[vj]:
mst.append((vi,vj),w)
if len(mst) == vnum - 1:
break
rep,orep = rep[vi],reps[vj]
for i in range(vnum): #合并连通分量
if reps[i] == orep:
reps[i] = rep
return mst
Prim算法
Prim算法基于最小生成树的一个重要性质,MST性质如下:
设G=(V,E)是一个网络,U是V的一个任意真子集,e为G的一条边,一个端点在U里,另一个不在,而且e的权值与其他同情况的边相比最小,那么G必有一棵包括边e的最小生成树
算法思想:
(1)从图G的顶点集V中任取一顶点放入集合U中,这时U = {v0},令边集合ET = {},显然T=(U,ET)是一棵树
(2)检查所有一个端点在集合U里而另一个端点在集合V-U的边,找出其中权最小的边,将不再U的顶点加入,并将e加入边集合ET
(3)重复步骤(2)直到U=V,这时子图T就是G的一棵最小生成树
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为V;初始令集合u={s},v=V−u;
- 在两个集合u,v能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息。
算法实现:
class PrioQueueError(ValueError):
pass
#使用list实现基于堆的优先序列
(这是额外的内容,帮助Prim算法的实现)
class PrioQueue:
def __init__(self,elist=[]):
self._elems = list(elist)
if elist:
self.buildheap()
def is_empty(self):
return not self._elems
def enqueue(self,e):
self._elems.append(None)
self.siftup(e,len(self._elems)-1)
def siftup(self,e,last):
elems,i,j = self._elems,last,(last-1)//2
while i > 0 and e < elems[j]:
elems[i] = elems[j]
i,j, = j,(j-1)//2
elems[i] = e
def dequeue(self):
if self.is_empty():
raise PrioQueueError('in dequeue')
elems = self._elems
e0 = elems[0]
e = elems.pop()
if len(elems) > 0:
self.siftdown(e,0,len(elems))
return e0
def siftdown(self,e,begin,end):
elems,i,j = self._elems,begin,begin*2+1
while j < end:
if j+1 < end and elems[j+1] < elems[j]:
j += 1
if e < elems[j]:
break
elems[i] = elems[j]
i,j = j,2*j+1
elems[i] = e
def buildheap(self):
end = len(self._elems)
for i in range(end//2.-1,-1):
self.siftdown(self._elems[i],i,end)
#Prim最小生成树法
def Prim(graph):
vnum = graph.vertex_num()
mst = [None]*vnum
cands = PrioQueue([(0,0,0)])
count = 0
while count < vnum and not cands.is_empty():
w,u,v = cands.dequeue()
if mst[v]:
continue
mst[v] = ((u,v),w)
count += 1
for vi,w in graph.out_edges(v):
if not mst[vi]:
cands.enqueue((w,v,vi))
return mst
最短路径问题
最短路径问题可以分为两种:
- 单源最短路径问题,即从一个顶点出发到图中其余各顶点的最短路径问题;
- 所有顶点之间的最短路径问题
单源最短路径的Dijkstra算法
-
算法特点:
迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
-
算法的思路
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合:T,初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,集合T只有顶点s。
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,OK,此时完成一个顶点,
然后,需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
算法实现:
import PrioQueue
#Dijkstra算法
def dijkstra_shortest_paths(graph,v0):
vnum = graph.vertex_num()
assert 0 <= v0 <= vnum
paths = [None]*vnum
count = 0
cands = PrioQueue([(0,v0,v0)]) #初始队列
while count < vnum and not cands.is_empty():
plen,u,vmin = cands.dequeue() #取顶点
if paths[vmin]:
continue
paths[vmin] = (u,plen) #记录路径
for v,w in graph.out_edges(vmin):
if not paths[v]:
cands.enqueue((plen + w,vmin,v))
count += 1
return paths
任意顶点间最短路径的Floyd算法
- 算法的特点:
弗洛伊德算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包。 - 算法的思路
通过Floyd计算图G=(V,E)中各个顶点的最短路径时,需要引入两个矩阵,矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素b[i][j],表示顶点i到顶点j经过了b[i][j]记录的值所表示的顶点。
假设图G中顶点个数为N,则需要对矩阵D和矩阵P进行N次更新。初始时,矩阵D中顶点a[i][j]的距离为顶点i到顶点j的权值;如果i和j不相邻,则a[i][j]=∞,矩阵P的值为顶点b[i][j]的j的值。 接下来开始,对矩阵D进行N次更新。第1次更新时,如果”a[i][j]的距离” > “a[i][0]+a[0][j]”(a[i][0]+a[0][j]表示”i与j之间经过第1个顶点的距离”),则更新a[i][j]为”a[i][0]+a[0][j]”,更新b[i][j]=b[i][0]。 同理,第k次更新时,如果”a[i][j]的距离” > “a[i][k-1]+a[k-1][j]”,则更新a[i][j]为”a[i][k-1]+a[k-1][j]”,b[i][j]=b[i][k-1]。更新N次之后,操作完成!
算法实现:
def all_shortest_paths(graph):
vnum = graph.vertex_num()
a = [[graph.get_edge(i,j) for j in range(vnum)] for i in range(vnum)]
nvertex = [[-1 if a[i][j] == inf else j for j in range(vnum)] for i in range(vnum)]
for k in range(vnum):
for i in range(vnum):
for j in range(vnum):
if a[i][j] > a[i][k] + a[k][j]:
a[i][j] = a[i][k] + a[k][k]
nevertex[i][j] = nevertex[i][k]
return (a,nevertex)
│ g1_adjGraph.py 图
│ g1_basic_graphs.py 图
│ g2_bfs_shortest_path.py 宽度优先最小路径
│ g2_bfs_zero_one_shortest_path.py 01最小路径
│ g2_breadth_first_search.py 宽度优先搜索
│ g2_breadth_first_search_2.py 宽度优先搜索
│ g2_breadth_first_search_shortest_path.py 宽度优先搜索最小路径
│ g3_depth_first_search.py 深度优先搜索
│ g3_depth_first_search_2.py 深度优先搜索
│ g4_dijkstra.py dijkstra算法
│ g4_dijkstra_2.py dijkstra算法
│ g4_dijkstra_algorithm.py dijkstra最短路径算法
│ g5_bellman_ford.py Bellman-Ford最短路径算法
│ g5_graphs_floyd_warshall.py floyd_warshall多源最短路径算法
│ g6_prim.py prim算法
│ g7_greedy_best_first.py 贪婪最佳优先搜索
│ g7_greedy_min_vertex_cover.py 贪婪最小顶点覆盖
│ __init__.py
│ 图Graph.md 学习笔记
│ 图基本操作的实现.md


