1.1.8 树Tree
1.1.8 树Tree
二叉排序树
二叉排序树又称为二叉查找树。它或者是一颗空树,或者是具有下列性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值均小于它的根结构的值;
- 若它的右子树不为空,则右子树上所有节点的值均大于它的根结构的值;
- 它的左、右子树也分别为二叉排序树。
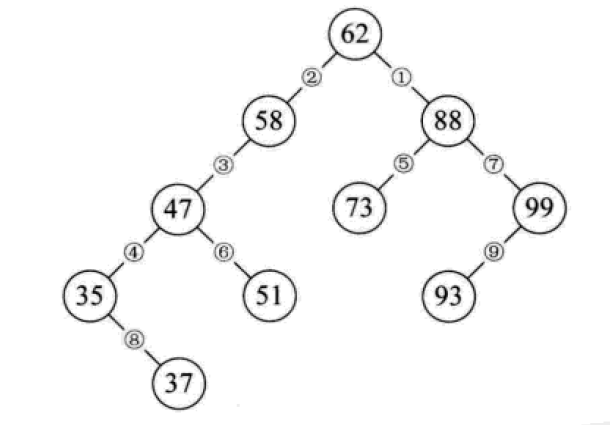
构造一颗二叉排序树的目的,往往不是为了排序,而是为了提高查找和插入删除关键字的速度。
二叉排序树的操作:
- 查找:对比节点的值和关键字,相等则表明找到了;小了则往节点的左子树去找,大了则往右子树去找,这么递归下去,最后返回布尔值或找到的节点。
- 插入:从根节点开始逐个与关键字进行对比,小了去左边,大了去右边,碰到子树为空的情况就将新的节点链接。
- 删除:如果要删除的节点是叶子,直接删;如果只有左子树或只有右子树,则删除节点后,将子树链接到父节点即可;如果同时有左右子树,则可以将二叉排序树进行中序遍历,取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。
二叉排序树总结:
- 二叉排序树以链式进行存储,保持了链接结构在插入和删除操作上的优点。
- 在极端情况下,查询次数为1,但最大操作次数不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状,也就引申出了后面的平衡二叉树。
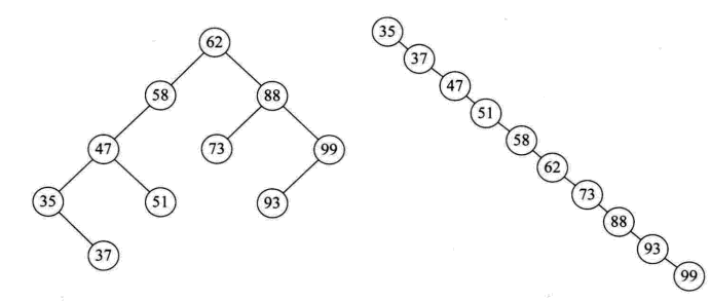
- 给定一个元素集合,可以构造不同的二叉排序树,当它同时是一个完全二叉树的时候,查找的时间复杂度为O(log(n)),近似于二分查找。
- 当出现最极端的斜树时,其时间复杂度为O(n),等同于顺序查找,效果最差。
平衡二叉树(AVL树)
平衡二叉树(AVL树,发明者的姓名缩写):一种高度平衡的排序二叉树,其每一个节点的左子树和右子树的高度差最多等于1。
平衡二叉树首先必须是一棵二叉排序树。
平衡因子(Balance Factor):将二叉树上节点的左子树深度减去右子树深度的值。
对于平衡二叉树所有包括分支节点和叶节点的平衡因子只可能是-1,0和1,只要有一个节点的因子不在这三个值之内,该二叉树就是不平衡的。
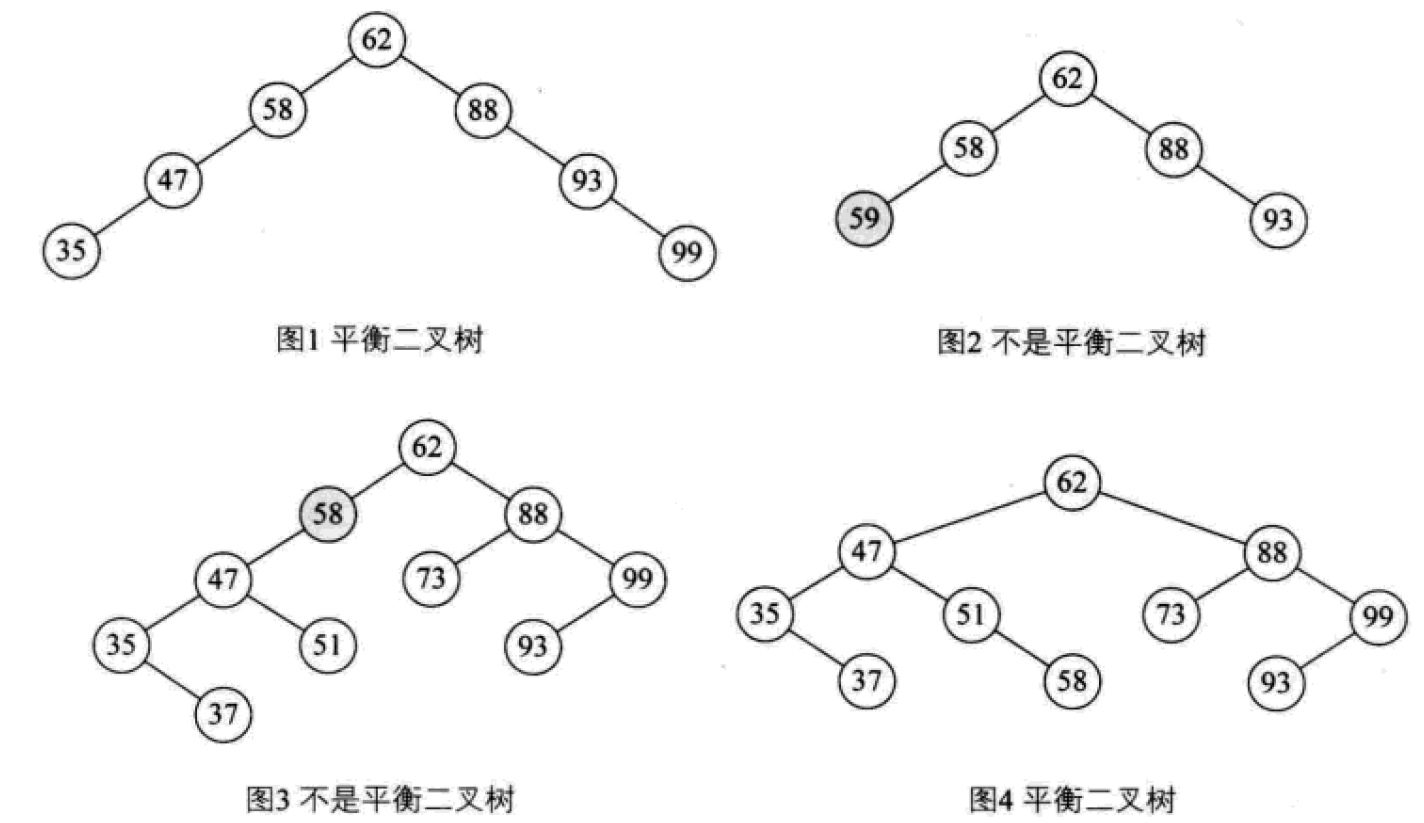
最小不平衡子树:距离插入结点最近的,且平衡因子的绝对值大于1的节点为根的子树。
平衡二叉树的构建思想:
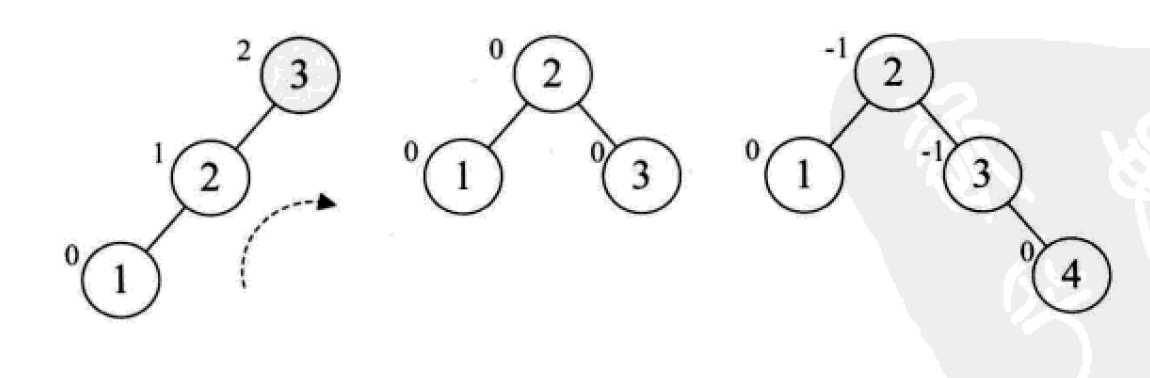
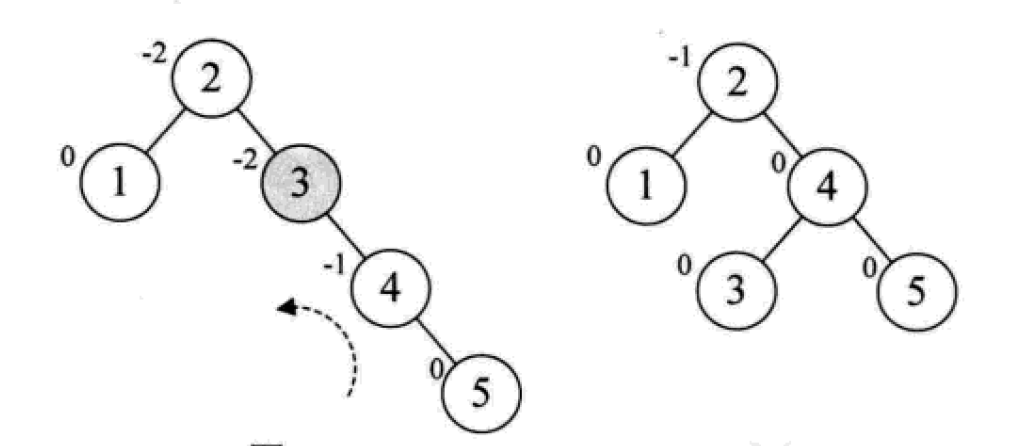
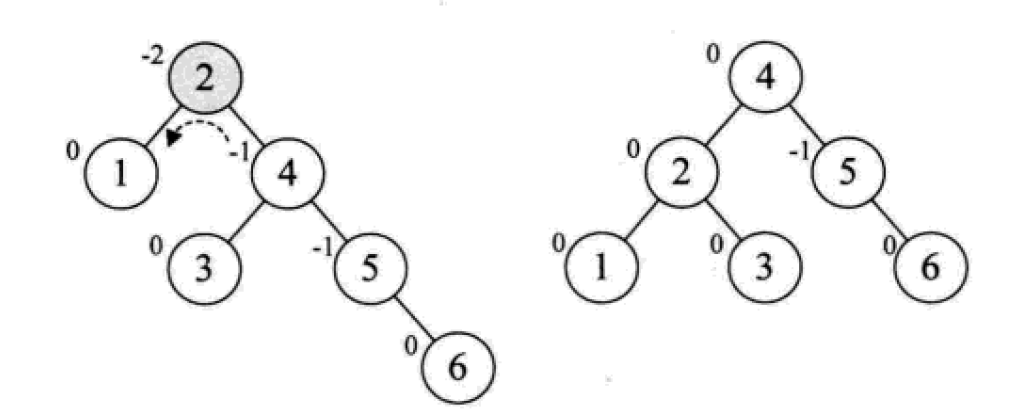
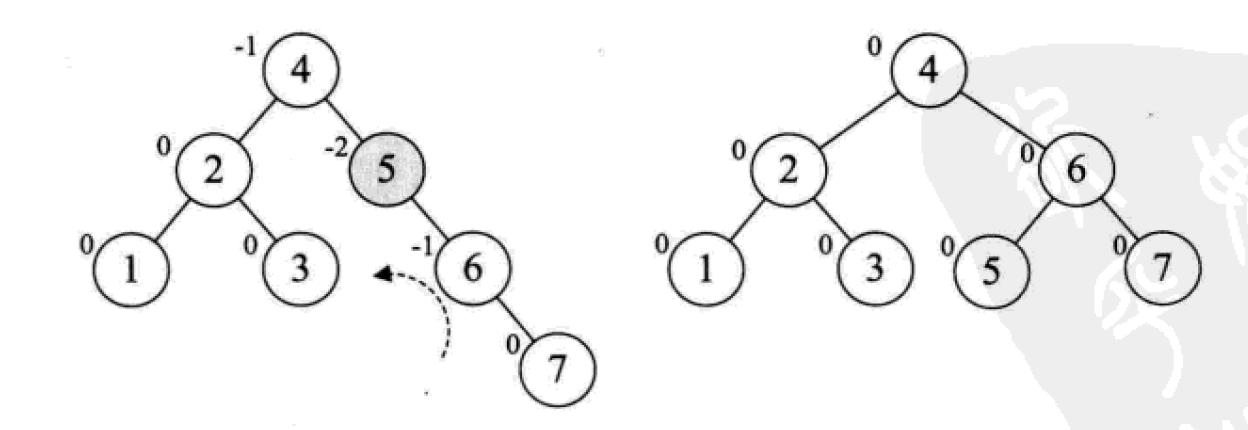
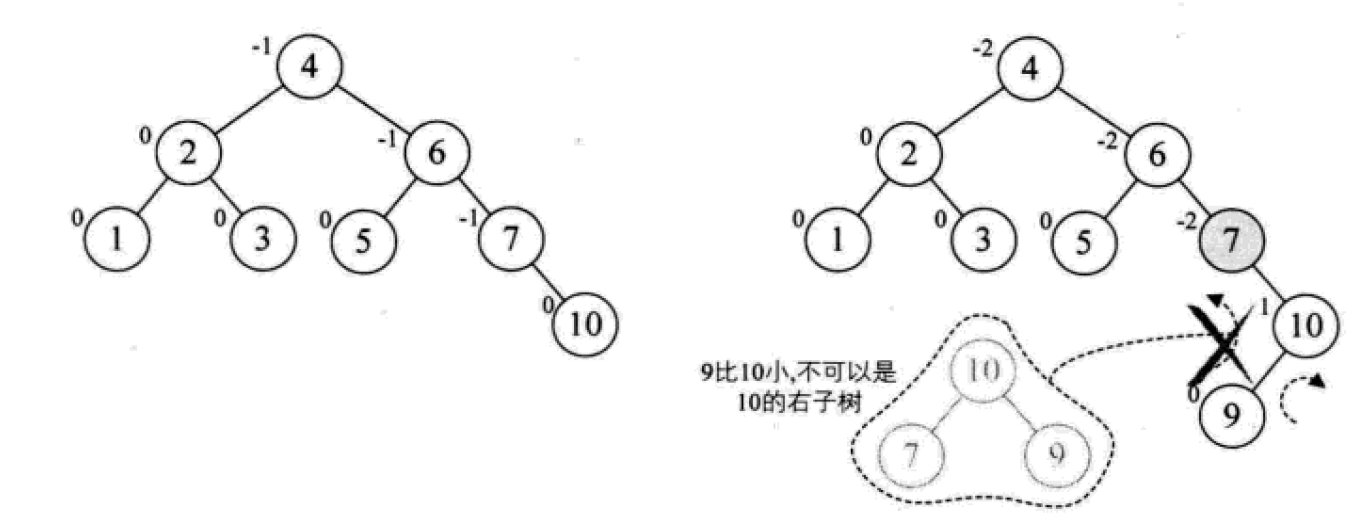
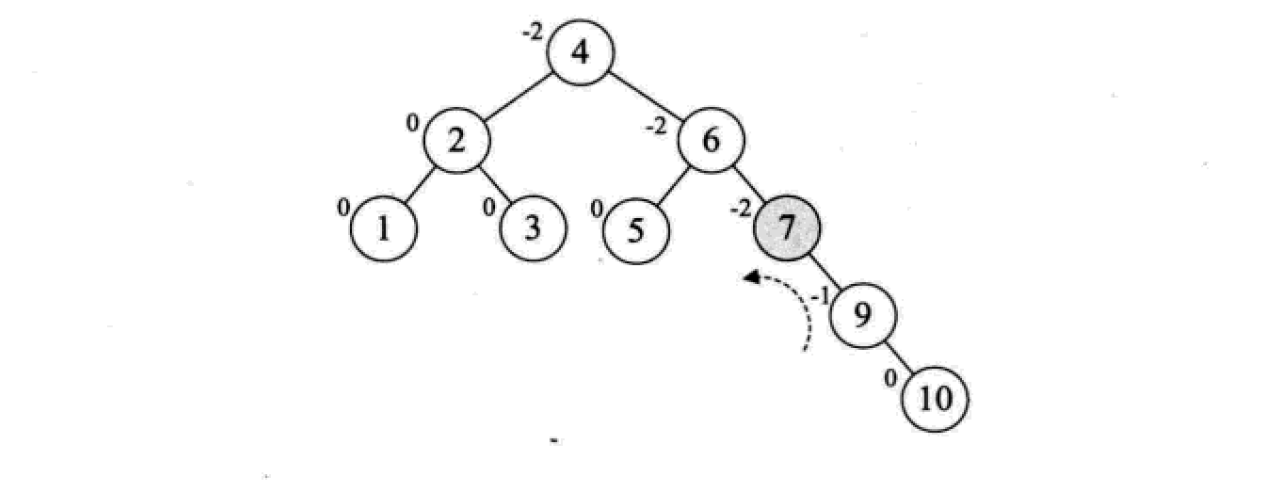
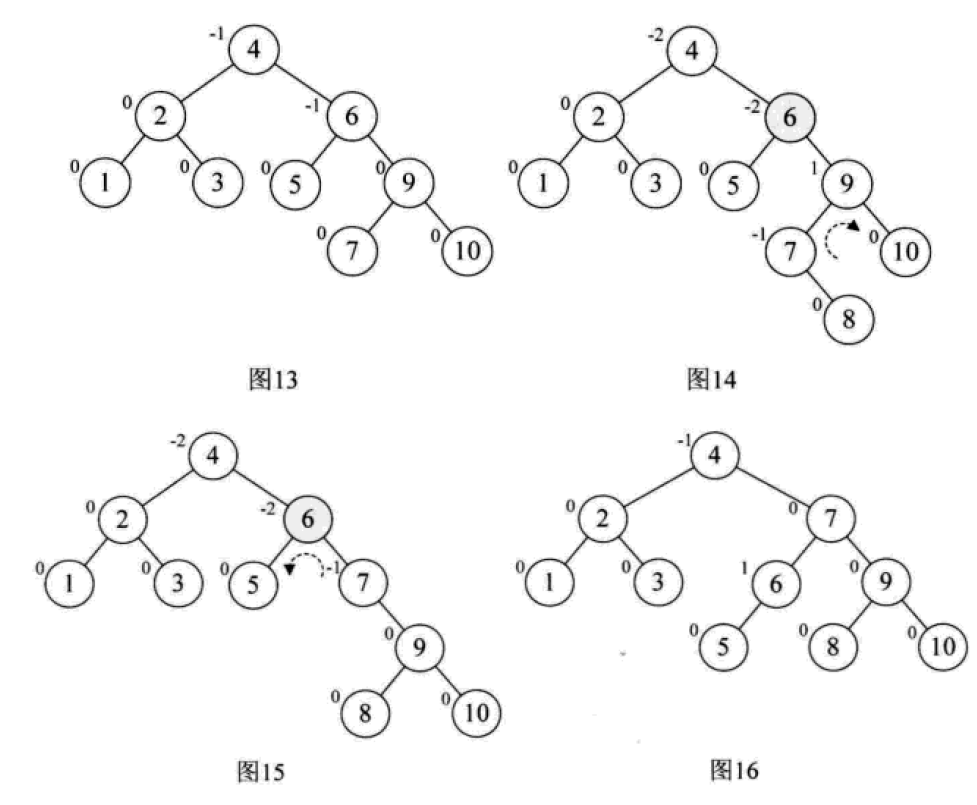
每当插入一个新结点时,先检查是否破坏了树的平衡性,若有,找出最小不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的连接关系,进行相应的旋转,成为新的平衡子树。
下面是由[1,2,3,4,5,6,7,10,9]构建平衡二叉树
多路查找树(B树)
多路查找树(muitl-way search tree):其每一个节点的孩子可以多于两个,且每一个结点处可以存储多个元素。
对于多路查找树,每个节点可以存储多少个元素,以及它的孩子数的多少是关键,常用的有这4种形式:2-3树、2-3-4树、B树和B+树。
2-3树
2-3树:每个结点都具有2个孩子,或者3个孩子,或者没有孩子。
一个2结点包含一个元素和两个孩子(或者没有孩子,不能只有一个孩子)。与二叉排序树类似,其左子树包含的元素都小于该元素,右子树包含的元素都大于该元素。
一个3结点包含两个元素和三个孩子(或者没有孩子,不能只有一个或两个孩子)。
2-3树中所有的叶子都必须在同一层次上。
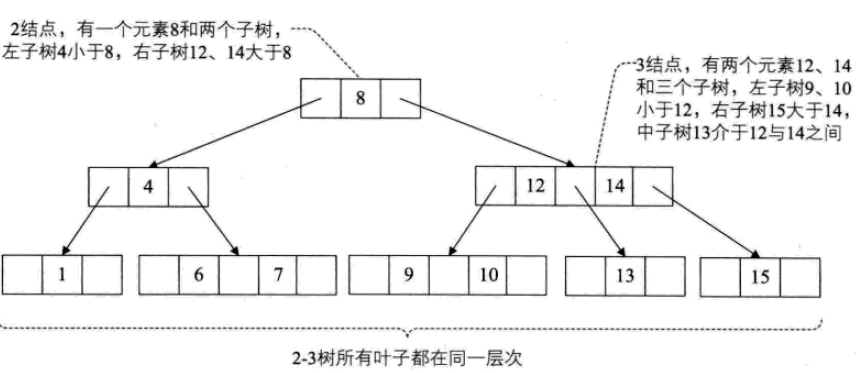
其插入操作如下:
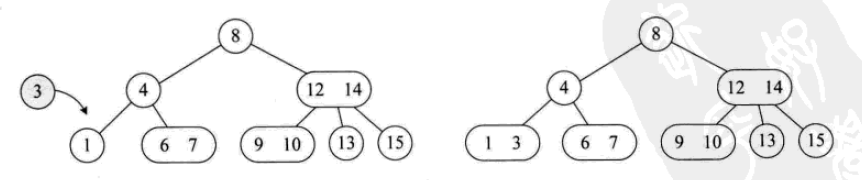
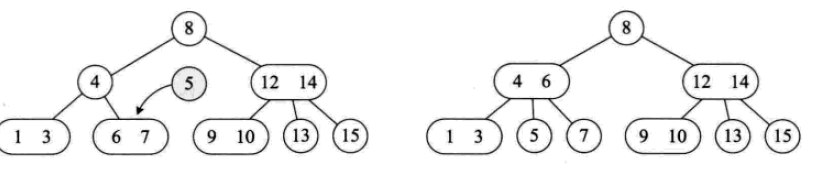
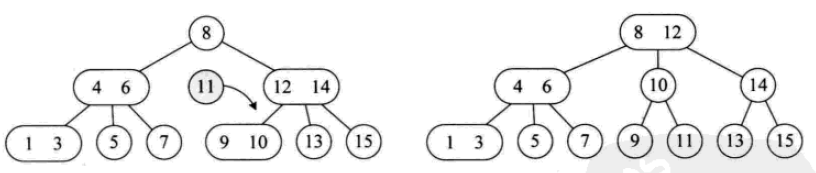
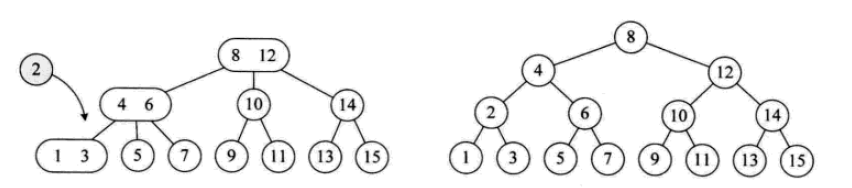
其删除操作如下:
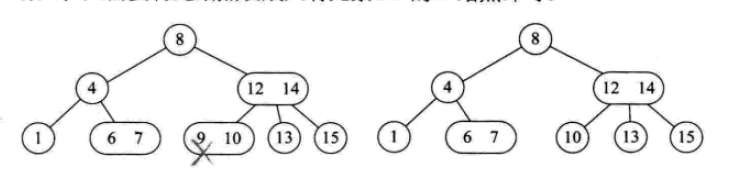
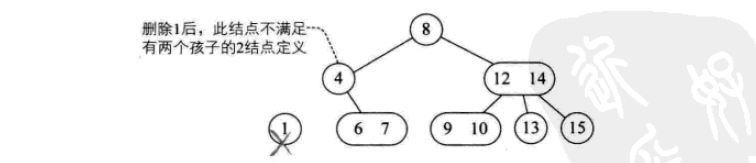
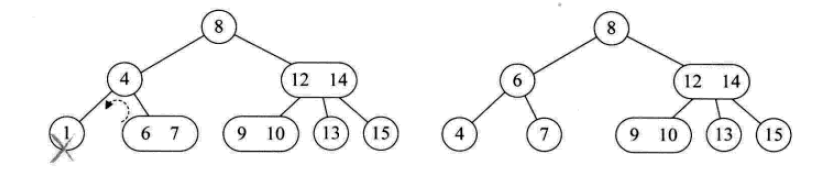

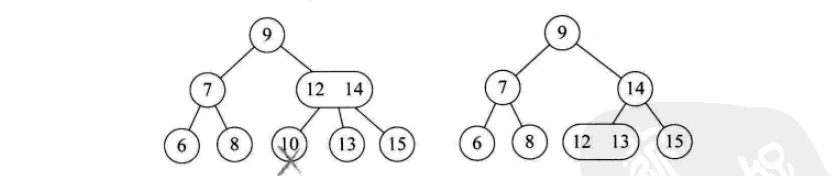
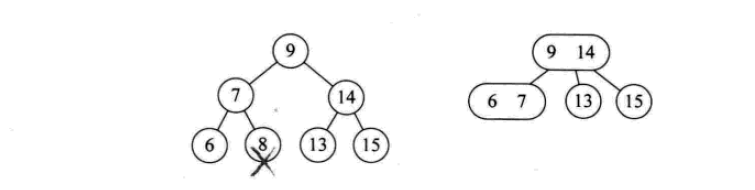

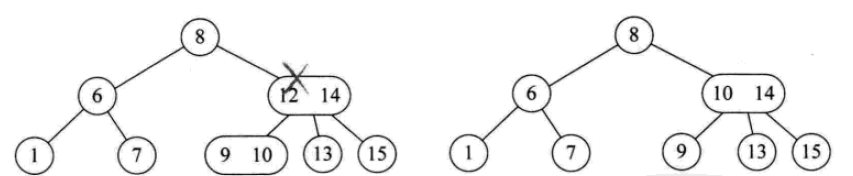
2-3-4树
其实就是2-3树的扩展,包括了4结点的使用。一个4结点包含小中大三个元素和四个孩子(或没有孩子)。
其插入操作:
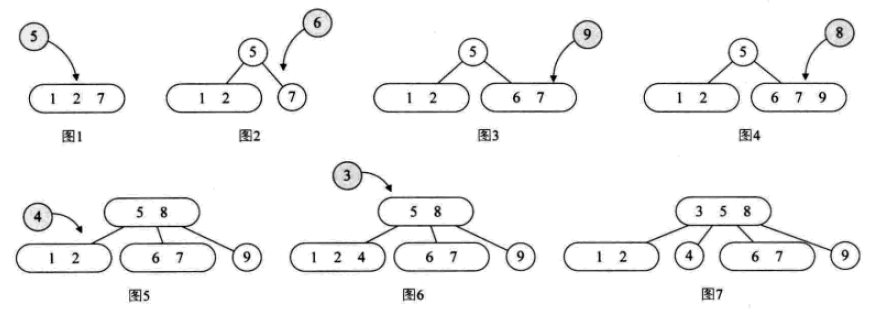
其删除操作:
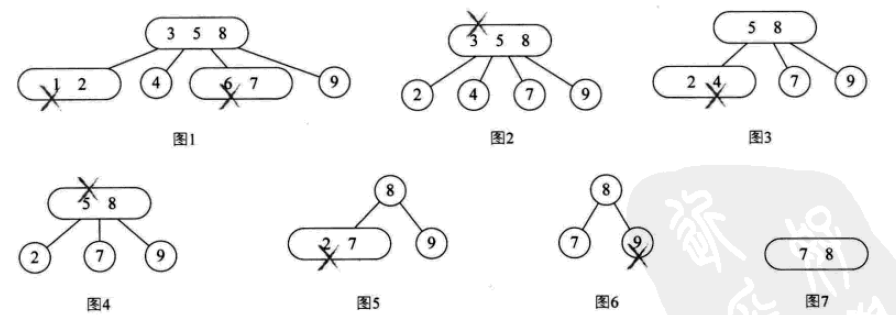
B树
B树是一种平衡的多路查找树。节点最大的孩子数目称为B树的阶(order)。2-3树是3阶B树,2-3-4是4阶B树。
B树的数据结构主要用在内存和外部存储器的数据交互中。


B+树
为了解决B树的所有元素遍历等基本问题,在原有的结构基础上,加入新的元素组织方式后,形成了B+树。
B+树是应文件系统所需而出现的一种B树的变形树,严格意义上将,它已经不是最基本的树了。
B+树中,出现在分支节点中的元素会被当做他们在该分支节点位置的中序后继者(叶子节点)中再次列出。另外,每一个叶子节点都会保存一个指向后一叶子节点的指针。
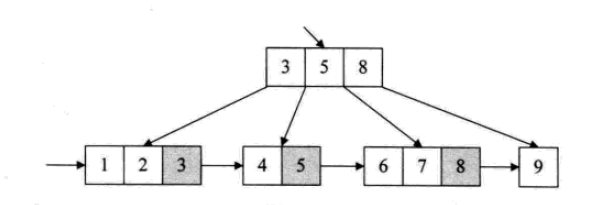
所有的叶子节点包含全部的关键字的信息,及相关指针,叶子节点本身依关键字的大小自小到大顺序链接
B+树的结构特别适合带有范围的查找。比如查找年龄在20~30岁之间的人。
树表查找
1. 二叉树查找
算法简介
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
**算法思想 **
二叉查找树(BinarySearch Tree)或者是一棵空树,或者是具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3)任意节点的左、右子树也分别为二叉查找树。 二叉查找树性质:对二叉查找树进行中序遍历,即可得到有序的数列。
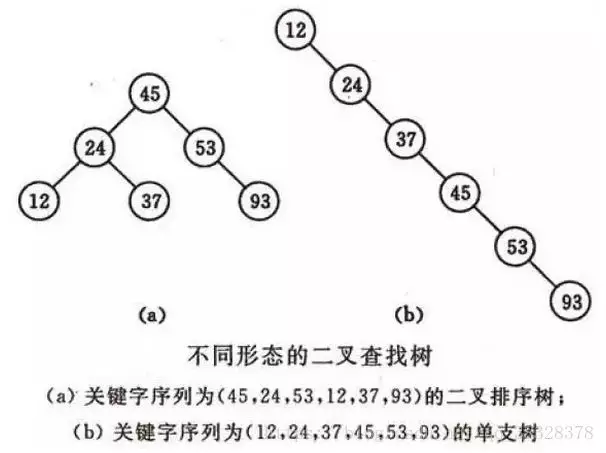
复杂度分析
它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
算法实现
# 二叉树查找 Python实现
class BSTNode:
"""
定义一个二叉树节点类。
以讨论算法为主,忽略了一些诸如对数据类型进行判断的问题。
"""
def __init__(self, data, left=None, right=None):
"""
初始化
:param data: 节点储存的数据
:param left: 节点左子树
:param right: 节点右子树
"""
self.data = data
self.left = left
self.right = right
class BinarySortTree:
"""
基于BSTNode类的二叉查找树。维护一个根节点的指针。
"""
def __init__(self):
self._root = None
def is_empty(self):
return self._root is None
def search(self, key):
"""
关键码检索
:param key: 关键码
:return: 查询节点或None
"""
bt = self._root
while bt:
entry = bt.data
if key < entry:
bt = bt.left
elif key > entry:
bt = bt.right
else:
return entry
return None
def insert(self, key):
"""
插入操作
:param key:关键码
:return: 布尔值
"""
bt = self._root
if not bt:
self._root = BSTNode(key)
return
while True:
entry = bt.data
if key < entry:
if bt.left is None:
bt.left = BSTNode(key)
return
bt = bt.left
elif key > entry:
if bt.right is None:
bt.right = BSTNode(key)
return
bt = bt.right
else:
bt.data = key
return
def delete(self, key):
"""
二叉查找树最复杂的方法
:param key: 关键码
:return: 布尔值
"""
p, q = None, self._root # 维持p为q的父节点,用于后面的链接操作
if not q:
print("空树!")
return
while q and q.data != key:
p = q
if key < q.data:
q = q.left
else:
q = q.right
if not q: # 当树中没有关键码key时,结束退出。
return
# 上面已将找到了要删除的节点,用q引用。而p则是q的父节点或者None(q为根节点时)。
if not q.left:
if p is None:
self._root = q.right
elif q is p.left:
p.left = q.right
else:
p.right = q.right
return
# 查找节点q的左子树的最右节点,将q的右子树链接为该节点的右子树
# 该方法可能会增大树的深度,效率并不算高。可以设计其它的方法。
r = q.left
while r.right:
r = r.right
r.right = q.right
if p is None:
self._root = q.left
elif p.left is q:
p.left = q.left
else:
p.right = q.left
def __iter__(self):
"""
实现二叉树的中序遍历算法,
展示我们创建的二叉查找树.
直接使用python内置的列表作为一个栈。
:return: data
"""
stack = []
node = self._root
while node or stack:
while node:
stack.append(node)
node = node.left
node = stack.pop()
yield node.data
node = node.right
if __name__ == '__main__':
lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
bs_tree = BinarySortTree()
for i in range(len(lis)):
bs_tree.insert(lis[i])
# bs_tree.insert(100)
bs_tree.delete(58)
for i in bs_tree:
print(i, end=" ")
# print("\n", bs_tree.search(4))
2. 平衡查找树之2-3查找树(2-3 Tree)
算法描述
2-3查找树定义
和二叉树不一样,2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node),他保存1个key和左右两个自己点。对应3节点(3-node),保存两个Key,2-3查找树的定义如下:
1)要么为空,要么:
2)对于2节点,该节点保存一个key及对应value,以及两个指向左右节点的节点,左节点也是一个2-3节点,所有的值都比key要小,右节点也是一个2-3节点,所有的值比key要大。
3)对于3节点,该节点保存两个key及对应value,以及三个指向左中右的节点。左节点也是一个2-3节点,所有的值均比两个key中的最小的key还要小;中间节点也是一个2-3节点,中间节点的key值在两个跟节点key值之间;右节点也是一个2-3节点,节点的所有key值比两个key中的最大的key还要大。
2-3查找树的性质
1)如果中序遍历2-3查找树,就可以得到排好序的序列;
2)在一个完全平衡的2-3查找树中,根节点到每一个为空节点的距离都相同。(这也是平衡树中“平衡”一词的概念,根节点到叶节点的最长距离对应于查找算法的最坏情况,而平衡树中根节点到叶节点的距离都一样,最坏情况也具有对数复杂度。)
复杂度分析
2-3树的查找效率与树的高度是息息相关的。
距离来说,对于1百万个节点的2-3树,树的高度为12-20之间,对于10亿个节点的2-3树,树的高度为18-30之间。
对于插入来说,只需要常数次操作即可完成,因为他只需要修改与该节点关联的节点即可,不需要检查其他节点,所以效率和查找类似。
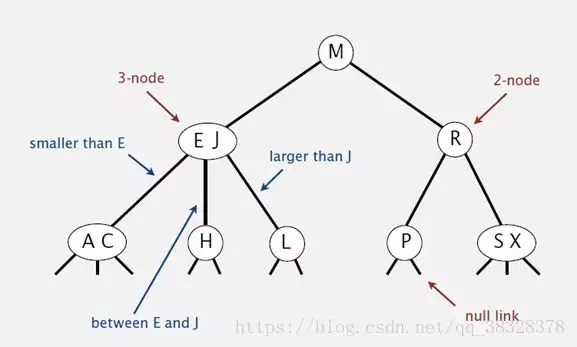
算法实现
class Node(object):
def __init__(self,key):
self.key1=key
self.key2=None
self.left=None
self.middle=None
self.right=None
def isLeaf(self):
return self.left is None and self.middle is None and self.right is None
def isFull(self):
return self.key2 is not None
def hasKey(self,key):
if (self.key1==key) or (self.key2 is not None and self.key2==key):
return True
else:
return False
def getChild(self,key):
if key<self.key1:
return self.left
elif self.key2 is None:
return self.middle
elif key<self.key2:
return self.middle
else:
return self.right
class 2_3_Tree(object):
def __init__(self):
self.root=None
def get(self,key):
if self.root is None:
return None
else:
return self._get(self.root,key)
def _get(self,node,key):
if node is None:
return None
elif node.hasKey(key):
return node
else:
child=node.getChild(key)
return self._get(child,key)
def put(self,key):
if self.root is None:
self.root=Node(key)
else:
pKey,pRef=self._put(self.root,key)
if pKey is not None:
newnode=Node(pKey)
newnode.left=self.root
newnode.middle=pRef
self.root=newnode
def _put(self,node,key):
if node.hasKey(key):
return None,None
elif node.isLeaf():
return self._addtoNode(node,key,None)
else:
child=node.getChild(key)
pKey,pRef=self._put(child,key)
if pKey is None:
return None,None
else:
return self._addtoNode(node,pKey,pRef)
def _addtoNode(self,node,key,pRef):
if node.isFull():
return self._splitNode(node,key,pRef)
else:
if key<node.key1:
node.key2=node.key1
node.key1=key
if pRef is not None:
node.right=node.middle
node.middle=pRef
else:
node.key2=key
if pRef is not None:
node.right=Pref
return None,None
def _splitNode(self,node,key,pRef):
newnode=Node(None)
if key<node.key1:
pKey=node.key1
node.key1=key
newnode.key1=node.key2
if pRef is not None:
newnode.left=node.middle
newnode.middle=node.right
node.middle=pRef
elif key<node.key2:
pKey=key
newnode.key1=node.key2
if pRef is not None:
newnode.left=Pref
newnode.middle=node.right
else:
pKey=node.key2
newnode.key1=key
if pRef is not None:
newnode.left=node.right
newnode.middle=pRef
node.key2=None
return pKey,newnode
3. 平衡查找树之红黑树(Red-Black Tree)
**红黑树的定义 **
红黑树是一种具有红色和黑色链接的平衡查找树,同时满足:
① 红色节点向左倾斜 ;
②一个节点不可能有两个红色链接;
③整个树完全黑色平衡,即从根节点到所以叶子结点的路径上,黑色链接的个数都相同。
红黑树的性质
整个树完全黑色平衡,即从根节点到所以叶子结点的路径上,黑色链接的个数都相同(2-3树的第2)性质,从根节点到叶子节点的距离都相等)。
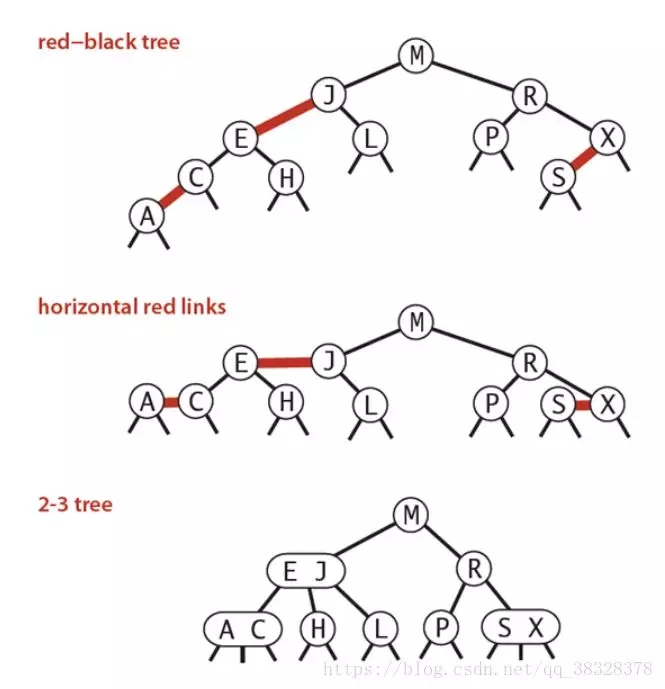
**复杂度分析 **
最坏的情况就是,红黑树中除了最左侧路径全部是由3-node节点组成,即红黑相间的路径长度是全黑路径长度的2倍。
下图是一个典型的红黑树,从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍:
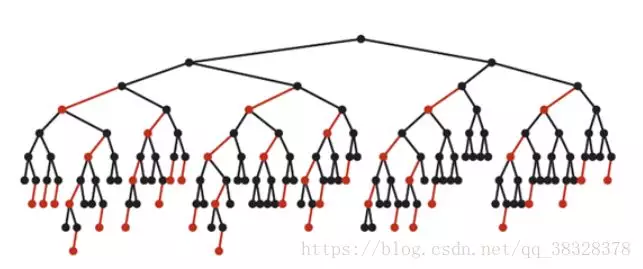
算法实现
#红黑树
from random import randint
RED = 'red'
BLACK = 'black'
class RBT:
def __init__(self):
# self.items = []
self.root = None
self.zlist = []
def LEFT_ROTATE(self, x):
# x是一个RBTnode
y = x.right
if y is None:
# 右节点为空,不旋转
return
else:
beta = y.left
x.right = beta
if beta is not None:
beta.parent = x
p = x.parent
y.parent = p
if p is None:
# x原来是root
self.root = y
elif x == p.left:
p.left = y
else:
p.right = y
y.left = x
x.parent = y
def RIGHT_ROTATE(self, y):
# y是一个节点
x = y.left
if x is None:
# 右节点为空,不旋转
return
else:
beta = x.right
y.left = beta
if beta is not None:
beta.parent = y
p = y.parent
x.parent = p
if p is None:
# y原来是root
self.root = x
elif y == p.left:
p.left = x
else:
p.right = x
x.right = y
y.parent = x
def INSERT(self, val):
z = RBTnode(val)
y = None
x = self.root
while x is not None:
y = x
if z.val < x.val:
x = x.left
else:
x = x.right
z.PAINT(RED)
z.parent = y
if y is None:
# 插入z之前为空的RBT
self.root = z
self.INSERT_FIXUP(z)
return
if z.val < y.val:
y.left = z
else:
y.right = z
if y.color == RED:
# z的父节点y为红色,需要fixup。
# 如果z的父节点y为黑色,则不用调整
self.INSERT_FIXUP(z)
else:
return
def INSERT_FIXUP(self, z):
# case 1:z为root节点
if z.parent is None:
z.PAINT(BLACK)
self.root = z
return
# case 2:z的父节点为黑色
if z.parent.color == BLACK:
# 包括了z处于第二层的情况
# 这里感觉不必要啊。。似乎z.parent为黑色则不会进入fixup阶段
return
# 下面的几种情况,都是z.parent.color == RED:
# 节点y为z的uncle
p = z.parent
g = p.parent # g为x的grandpa
if g is None:
return
# return 这里不能return的。。。
if g.right == p:
y = g.left
else:
y = g.right
# case 3-0:z没有叔叔。即:y为NIL节点
# 注意,此时z的父节点一定是RED
if y == None:
if z == p.right and p == p.parent.left:
# 3-0-0:z为右儿子,且p为左儿子,则把p左旋
# 转化为3-0-1或3-0-2的情况
self.LEFT_ROTATE(p)
p, z = z, p
g = p.parent
elif z == p.left and p == p.parent.right:
self.RIGHT_ROTATE(p)
p, z = z, p
g.PAINT(RED)
p.PAINT(BLACK)
if p == g.left:
# 3-0-1:p为g的左儿子
self.RIGHT_ROTATE(g)
else:
# 3-0-2:p为g的右儿子
self.LEFT_ROTATE(g)
return
# case 3-1:z有黑叔
elif y.color == BLACK:
if p.right == z and p.parent.left == p:
# 3-1-0:z为右儿子,且p为左儿子,则左旋p
# 转化为3-1-1或3-1-2
self.LEFT_ROTATE(p)
p, z = z, p
elif p.left == z and p.parent.right == p:
self.RIGHT_ROTATE(p)
p, z = z, p
p = z.parent
g = p.parent
p.PAINT(BLACK)
g.PAINT(RED)
if p == g.left:
# 3-1-1:p为g的左儿子,则右旋g
self.RIGHT_ROTATE(g)
else:
# 3-1-2:p为g的右儿子,则左旋g
self.LEFT_ROTATE(g)
return
# case 3-2:z有红叔
# 则涂黑父和叔,涂红爷,g作为新的z,递归调用
else:
y.PAINT(BLACK)
p.PAINT(BLACK)
g.PAINT(RED)
new_z = g
self.INSERT_FIXUP(new_z)
def DELETE(self, val):
curNode = self.root
while curNode is not None:
if val < curNode.val:
curNode = curNode.left
elif val > curNode.val:
curNode = curNode.right
else:
# 找到了值为val的元素,正式开始删除
if curNode.left is None and curNode.right is None:
# case1:curNode为叶子节点:直接删除即可
if curNode == self.root:
self.root = None
else:
p = curNode.parent
if curNode == p.left:
p.left = None
else:
p.right = None
elif curNode.left is not None and curNode.right is not None:
sucNode = self.SUCCESOR(curNode)
curNode.val, sucNode.val = sucNode.val, curNode.val
self.DELETE(sucNode.val)
else:
p = curNode.parent
if curNode.left is None:
x = curNode.right
else:
x = curNode.left
if curNode == p.left:
p.left = x
else:
p.right = x
x.parent = p
if curNode.color == BLACK:
self.DELETE_FIXUP(x)
curNode = None
return False
def DELETE_FIXUP(self, x):
p = x.parent
# w:x的兄弟结点
if x == p.left:
w = x.right
else:
w = x.left
# case1:x的兄弟w是红色的
if w.color == RED:
p.PAINT(RED)
w.PAINT(BLACK)
if w == p.right:
self.LEFT_ROTATE(p)
else:
self.RIGHT_ROTATE(p)
if w.color == BLACK:
# case2:x的兄弟w是黑色的,而且w的两个孩子都是黑色的
if w.left.color == BLACK and w.right.color == BLACK:
w.PAINT(RED)
if p.color == BLACK:
return
else:
p.color = BLACK
self.DELETE_FIXUP(p)
# case3:x的兄弟w是黑色的,而且w的左儿子是红色的,右儿子是黑色的
if w.left.color == RED and w.color == BLACK:
w.left.PAINT(BLACK)
w.PAINT(RED)
self.RIGHT_ROTATE(w)
# case4:x的兄弟w是黑色的,而且w的右儿子是红
if w.right.color == RED:
p.PAINT(BLACK)
w.PAINT(RED)
if w == p.right:
self.LEFT_ROTATE(p)
else:
self.RIGHT_ROTATE(p)
def SHOW(self):
self.DISPLAY1(self.root)
return self.zlist
def DISPLAY1(self, node):
if node is None:
return
self.DISPLAY1(node.left)
self.zlist.append(node.val)
self.DISPLAY1(node.right)
def DISPLAY2(self, node):
if node is None:
return
self.DISPLAY2(node.left)
print(node.val)
self.DISPLAY2(node.right)
def DISPLAY3(self, node):
if node is None:
return
self.DISPLAY3(node.left)
self.DISPLAY3(node.right)
print(node.val)
class RBTnode:
'''红黑树的节点类型'''
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.parent = None
def PAINT(self, color):
self.color = color
def zuoxuan(b, c):
a = b.parent
a.left = c
c.parent = a
b.parent = c
c.left = b
if __name__ == '__main__':
rbt=RBT()
b = []
for i in range(100):
m = randint(0, 500)
rbt.INSERT(m)
b.append(m)
a = rbt.SHOW()
b.sort()
equal = True
for i in range(100):
if a[i] != b[i]:
equal = False
break
if not equal:
print('wrong')
else:
print('OK!')
4. B树和B+树(B Tree/B+ Tree)
B树算法简介
B 树可以看作是对2-3查找树的一种扩展,即他允许每个节点有M-1个子节点。
①根节点至少有两个子节点;
②每个节点有M-1个key,并且以升序排列;
③位于M-1和M key的子节点的值位于M-1 和M key对应的Value之间;
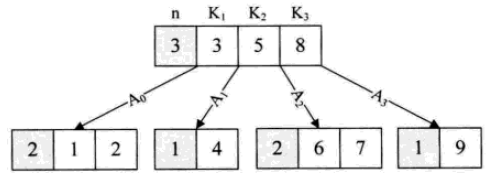
④非叶子结点的关键字个数=指向儿子的指针个数-1;
⑤非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] ;
⑥其它节点至少有M/2个子节点;
⑦所有叶子结点位于同一层; 如:(M=3)
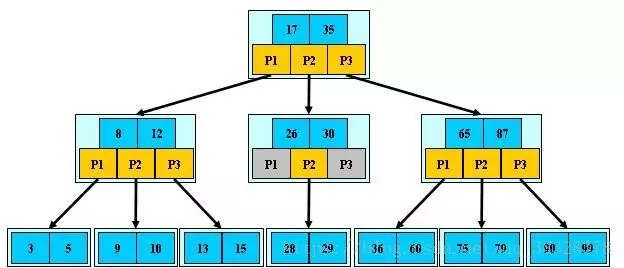
**B树算法思想 **
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
B树的特性
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少利用率,其最底搜索性能为O(LogN)
B+ 树算法简介
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
4.B-树是开区间;
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
如:(M=3)
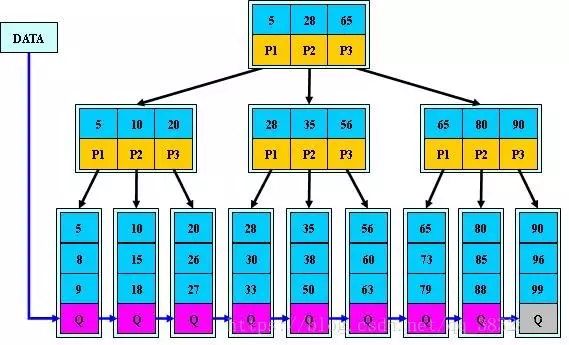
B+树算法思想
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+树的特性
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统;
算法实现
# -*- coding: UTF-8 -*-
# B树查找
class BTree: #B树
def __init__(self,value):
self.left=None
self.data=value
self.right=None
def insertLeft(self,value):
self.left=BTree(value)
return self.left
def insertRight(self,value):
self.right=BTree(value)
return self.right
def show(self):
print(self.data)
def inorder(node): #中序遍历:先左子树,再根节点,再右子树
if node.data:
if node.left:
inorder(node.left)
node.show()
if node.right:
inorder(node.right)
def rinorder(node): #倒中序遍历
if node.data:
if node.right:
rinorder(node.right)
node.show()
if node.left:
rinorder(node.left)
def insert(node,value):
if value > node.data:
if node.right:
insert(node.right,value)
else:
node.insertRight(value)
else:
if node.left:
insert(node.left,value)
else:
node.insertLeft(value)
if __name__ == "__main__":
l=[88,11,2,33,22,4,55,33,221,34]
Root=BTree(l[0])
node=Root
for i in range(1,len(l)):
insert(Root,l[i])
print("中序遍历(从小到大排序 )")
inorder(Root)
print("倒中序遍历(从大到小排序)")
rinorder(Root)
**5. 树表查找总结 **
二叉查找树平均查找性能不错,为O(logn),但是最坏情况会退化为O(n)。
在二叉查找树的基础上进行优化,我们可以使用平衡查找树。平衡查找树中的2-3查找树,这种数据结构在插入之后能够进行自平衡操作,从而保证了树的高度在一定的范围内进而能够保证最坏情况下的时间复杂度。但是2-3查找树实现起来比较困难,红黑树是2-3树的一种简单高效的实现,他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树,应用非常广泛,很多编程语言的内部实现都或多或少的采用了红黑树。
除此之外,2-3查找树的另一个扩展——B/B+平衡树,在文件系统和数据库系统中有着广泛的应用。
线段树(segment tree)
线段树(segment tree),顾名思义, 是用来存放给定区间(segment, or interval)内对应信息的一种数据结构。与树状数组(binary indexed tree)相似,线段树也用来处理数组相应的区间查询(range query)和元素更新(update)操作。与树状数组不同的是,线段树不止可以适用于区间求和的查询,也可以进行区间最大值,区间最小值(Range Minimum/Maximum Query problem)或者区间异或值的查询。
线段树是用一个完全二叉树来存储对应于其每一个区间(segment)的数据。该二叉树的每一个结点中保存着相对应于这一个区间的信息。同时,线段树所使用的这个二叉树是用一个数组保存的。
例如:数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树(背景为白色表示叶子节点,非叶子节点的值是其对应数组区间内的最小值,例如根节点表示数组区间arr[0...5]内的最小值是1):
区间信息:该区间上的最小值
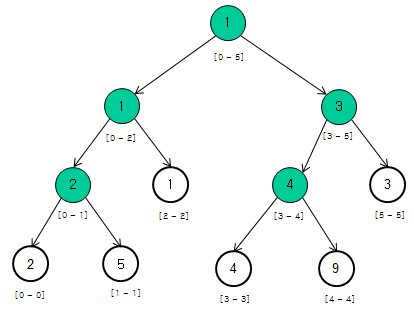
Interval tree?
线段树Lazy-tag
线段树求区间极值的时候,每次都需要修改包含在插入区间的所有节点,另外大多数线段树不一定是单点加/减权值,会在区间里集体增减。这样恶化时间复杂度,所以用了懒惰标记来优化。
成段更新用到延迟标记(或者说懒惰标记),简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要更新或查询到的时候再操作。
二分索引树(Fenwick Tree)
Fenwick Tree 又叫二分索引树(Binary Index Tree),是一种树状结构的数组。主要用来存储频次信息或者用于计算累计频次表等。
树状数组是用来解决在数组元素动态变化的情况下,高效的计算子数组和的一种数据结构,其更新效率和计算和的效率均为O(logn)。核心思想为:
- 树状数组C[]中的每个元素是原数组中一个或者多个连续元素的和。
- 在进行连续求和操作A[1]+…+A[n]时,只需要将树状数组中某几个元素求和即可。
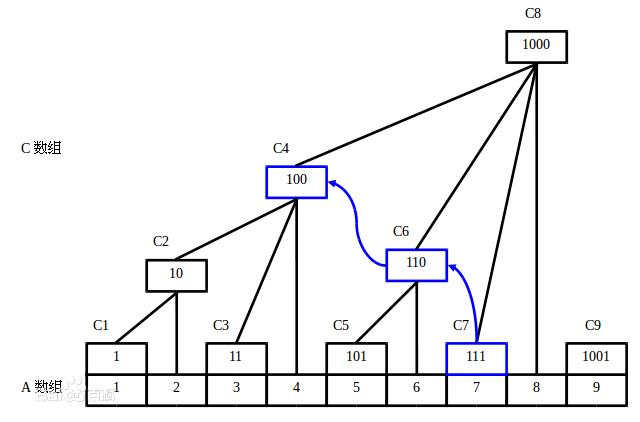
如图并不是每个节点都代表自己前面所有元素的和。只有满足2n 这样的节点才代表自己前面所有元素的和(二进制尾数有n个0,则该节点为前2n个元素的和,如C6尾有1个0,C6=A5+A6)。
对于数组A[1], A[2]...A[8]来说,树状数组节点C[i]:
C[1]=A[1]
C[2]=A[1]+A[2]
C[3]=A[3]
C[4]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
C[6]=A[5]+A[6]
C[7]=A[7] (sum(A[1]+...+A[7]) = C[7]+C[6]+C[4])
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8] (sum(A[1]+...+A[8]) = C[8])
Ci = Ai-lowbit(i)+1+A i-lowbit(i)+2+…Ai
lowbit(x) = x & (-x); lowbit(x)函数返回x的二进制表示最右位1所代表的值。如:
对于(1)2,(10)2,(11)2,(100)2,(101)2,(110)2,(1111)2,(1000)2,...
lowbit(1)=1 lowbit(2)=2 lowbit(3)=1 lowbit(4)=4 lowbit(5)=1 lowbit(6)=2 lowbit(8)=8...
将lowbit(x)代入Ci = Ai-lowbit(i)+1+A i-lowbit(i)+2+…Ai即可得到节点C[i]的值
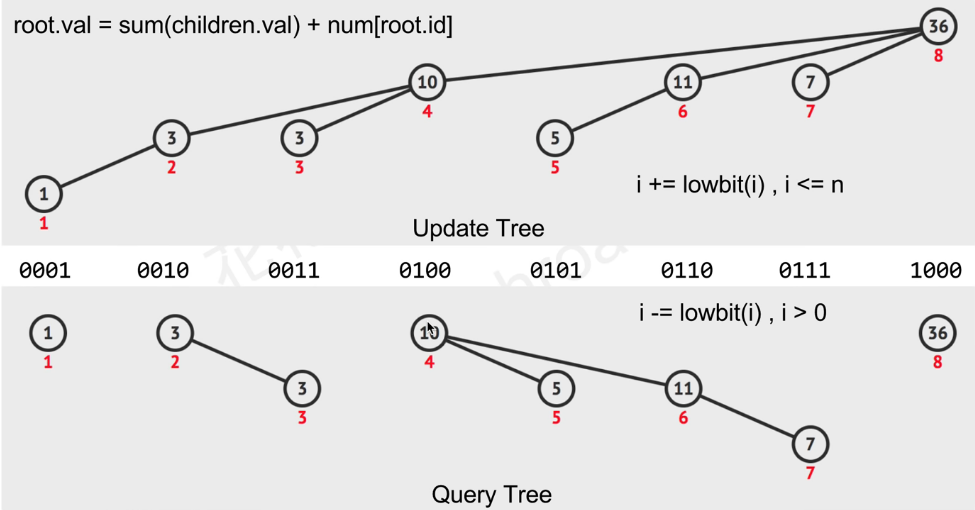
更新
更新节点i的值,则要把受其影响的所有索引(i+=lowbit(i), i<=n)的值都更新。如:更新节点5的值,则要把其值同步更新到其父节点6,8。
查询
查询数组A索引1到i的和,则需要把索引(i-=lowbit(i), i>0)的值求和。如:sum(A[1]+...+A[7]) = C[7]+C[6]+C[4]
算法实现
def update(self, i, val): # update data (adding) in index i in O(lg N)
while i < self.Size:
self.ft[i] += val
i += i & (-i)
def query(self, i): # query cumulative data from index 0 to i in O(lg N)
ret = 0
while i > 0:
ret += self.ft[i]
i -= i & (-i)
return ret
字典树(Trie Tree)
Trie树,又叫字典树、前缀树(Prefix Tree)、单词查找树 或 键树,是一种多叉树结构。如下图:
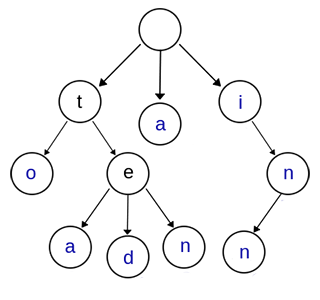
上图是一棵Trie树,表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”} 。从上图可以归纳出Trie树的基本性质:
- 根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
- 从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符互不相同。
通常在实现的时候,会在节点结构中设置一个标志,用来标记该结点处是否构成一个单词(关键字)。
可以看出,Trie树的关键字一般都是字符串,而且Trie树把每个关键字保存在一条路径上,而不是一个结点中。另外,两个有公共前缀的关键字,在Trie树中前缀部分的路径相同,所以Trie树又叫做前缀树(Prefix Tree)。
Trie树的优缺点
Trie树的核心思想是空间换时间,利用字符串的公共前缀来减少无谓的字符串比较以达到提高查询效率的目的。
优点
-
插入和查询的效率很高,都为O(m),其中 m 是待插入/查询的字符串的长度。
- 关于查询:hash 表时间复杂度是O(1),但是哈希搜索的效率通常取决于 hash 函数的好坏,若一个坏的 hash 函数导致很多的冲突,效率并不一定比Trie树高。
-
Trie树中不同的关键字不会产生冲突。
-
Trie树只有在允许一个关键字关联多个值的情况下才有类似hash碰撞发生。
-
Trie树不用求 hash 值,对短字符串有更快的速度。通常,求hash值也是需要遍历字符串的。
-
Trie树可以对关键字按字典序排序。
缺点
-
当 hash 函数很好时,Trie树的查找效率会低于哈希搜索。
-
空间消耗比较大。
Trie树的应用
1、字符串检索
检索/查询功能是Trie树最原始的功能。思路就是从根节点开始一个一个字符进行比较:
- 如果沿路比较,发现不同的字符,则表示该字符串在集合中不存在。
- 如果所有的字符全部比较完并且全部相同,还需判断最后一个节点的标志位(标记该节点是否代表一个关键字)。
2、词频统计
Trie树常被搜索引擎系统用于文本词频统计 。
思路:为了实现词频统计,我们修改了节点结构,用一个整型变量count来计数。对每一个关键字执行插入操作,若已存在,计数加1,若不存在,插入后count置1。
注意:第一、第二种应用也都可以用 hash table 来做。
3、字符串排序
Trie树可以对大量字符串按字典序进行排序,思路也很简单:遍历一次所有关键字,将它们全部插入trie树,树的每个结点的所有儿子很显然地按照字母表排序,然后先序遍历输出Trie树中所有关键字即可。
4、前缀匹配
例如:找出一个字符串集合中所有以ab开头的字符串。我们只需要用所有字符串构造一个trie树,然后输出以a->b->开头的路径上的关键字即可。
trie树前缀匹配常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。
5、作为其他数据结构和算法的辅助结构
如后缀树,AC自动机等。
小波树(WaveletTree)[1]
Succinct简洁数据结构是一种来自生物信息学的研究成果,是在数据压缩存储达到接近信息熵下界时仍然保持高效的查询性能的一类数据结构,通俗点说就是既能压缩存储还能高速检索。Succinct数据结构有很多,小波树(wavelet tree)是其中最常见有效的之一。
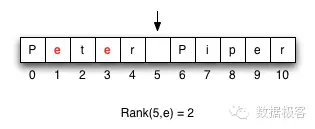
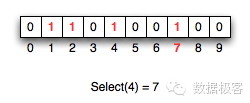
小波树总体上是针对一个字符串构造的一种数据结构,用来回答Rank和Select这样的查询。Rank操作代表这样的含义:对于一个{0,1}构造的位图向量,Rank(position,1)的含义是位图中position位置之前1的数量。那么对于一个字符串来说,Rank(position, alpha)代表字符串中position位置之前字符alpha的数量,例如下图的字符串中,Rank(5,e) = 2。
Select是Rank的反向操作:对于一个{0,1}构造的位图向量,Select(frequency,1)代表第frequency次出现{1}的位置。例如在下面的位图向量中,Select(4,1) = 7。
能够有效支持Rank/Select操作的位图向量是许多Succinct数据结构构造的基石,也包括小波树。假如位图向量可以正好放入一个word中,比如64bit,那么Rank其实就是一次popcnt操作,Intel的CPU可以采用SSE指令在几个周期内完成该操作。当位图扩大之后,为了能够支持高速的Rank操作,就需要设计内存布局,使得最终的操作都将转化为单个word之上的popcnt,因此Rank性能的瓶颈将取决于cache miss的次数——一次cache miss将导致最长100ns的延迟,相比之下几个指令周期的popcnt可以忽略不计。在Succinct数据结构刚刚出现的时候,早期的位图向量做一次Rank操作需要至少5,6次cache miss,后来日本人Takeshi发明了3次cache miss的位图向量,而我们此前团队的August进一步改进,做到了仅需1次cache miss,这是目前最优的位图向量布局。相比Rank操作,Select要昂贵得多,可以类比数学中的积分对比求导的性能差异。
下边我们来看一下最常见的二叉小波树是如何构造的。二叉小波树构造过程就是把字符串转化为一颗平衡二叉树位图的过程,0代表一半的符号,1代表另一半符号。在树的每一层,字符表都要重新编码,直到最底层没有任何歧义。递归的构造过程如下:
- 取字符串的字母表,将前半部分编码为0,后半部分编码为1,例如{a,b,c,d}就变成了{0,0,1,1}。这个时候编码是有歧义的,比如你不能根据0就猜测该字符是a还是b。
- 把0表示的字符{a,b}分组做为一个子树;把1表示的字符{c,d}分组做为另一颗一个子树。
- 在每一颗上都重复如上步骤直到子树只包含1个或者2个字符,这样0或者1就可以明确表示而没有任何歧义了。
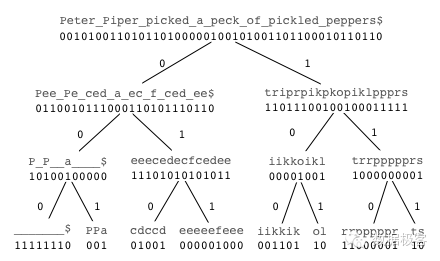
例如对于字符串"Peter Piper picked a peck of pickled peppers",构造出的二叉小波树如图所示,这里,空格和字符串终止符我们分别特殊符号来表示,比如""和"\(",那么整个串的字符表包含{\),P,,a,c,d,e,f,i,k,l,o,p,r,s,t}, 首先它们会被编码映射成{0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1},左边的子树基于编码为0的字符集创建,包含{$,P,_,a,c,d,e,f} 然后该子树重新编码为{0,0,0,0,1,1,1,1},再重复子树创建过程。
可以看到整个二叉树是平衡的,因此,我们可以把每层所有的位图连接在一起合并成一个大的位图,这样树的每一层都是一个等长的位图,而树的高度则是字符集尺寸的对数O(log_2{A})。
在一个小波树构造好之后,一个字符串上的rank操作需要从树的最顶端位图开始操作,直到最底层的位图,因此一共需要N次位图上的rank操作,这里N等于小波树的高度。例如查询Rank(5,e)的过程可以由图看出来:首先在最上层,{e}我们编码为0,因此在这一层执行rank(5,0)的操作,我们可以得到0的数量是4。
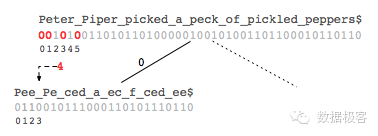
这个结果可以引导我们到下一层从那个位置开始执行rank操作——在{0}表示的子树中,第4个位置,由于在该层{e}已经编码为1,因此我们需要执行rank(4,1),重复该步骤直到最底层。
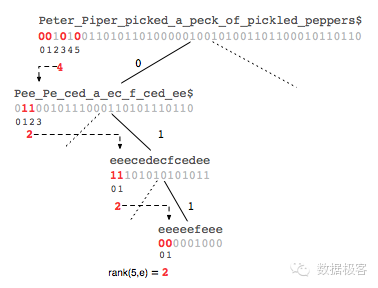
除了二叉小波树之外,还有霍夫曼小波树,针对文本型序列可以提供更高的压缩比,以及更加快速的小波矩阵。
那么拥有可以提供Rank/Select能力的小波树,我们都可以做一些什么工作呢?这里有一些基于Rank/Select的扩展型查询:
- Lookup(T, p) : 在一个字符串序列T,返回位置在p的序列项。
- Quantile(T, p, sp, ep) : 在一个字符串序列T,返回位置在sp和ep之间的第p个最大值。
- FreqList (T, k, sp, ep) : 在一个字符串序列T,返回位置在sp和ep之间的最频繁的k个值。
- RangeList (T, sp, ep, min, max) : 在一个字符串序列T,返回位置在sp和ep之间,取值范围在min和max之间的所有项。
- RangeList (T, sp, ep, min, max) : 在一个字符串序列T,返回位置在sp和ep之间,取值范围在min和max之间的所有项的频率。
这些扩展型查询基本都是围绕一个字符串序列某个区间之内的统计信息来做,聪明的读者一定可以想到可以拿它来做数据分析。它们大部分的复杂度跟Rank/Select相差不大,都是正比于小波树的高度。因此可以看到,如果拿小波树去表示一个序列,不论该序列有多长,查询性能都不受影响,因为它只受限于序列字符集的大小。举例来说,如果小波树表示的是中文文本,那么任何操作的时间只跟log_2(65536)这个值有关,这意味着小波树的高度最多只有16层,这是效率多么惊人的数据结构!当然,在实际工程实现中,还会受到其他的限制,比如cache miss,内存分配,等等。做为一个压缩型的数据结构,表征全部文本,所消耗的空间最多只有16个位图向量。
如果嫌上边的叙述仍然过于抽象,我们接下来可以举一些更加实际的例子。
第一个例子是全文搜索。全文搜索的意思是,给定一段文本,我们可以快速的查询任意子串是否在该文本中出现,并且统计它的频率和出现的位置。常规的做法是构造后缀树或者后缀数组,Ferragina和Manzini在前人工作的基础之上把经过BWT变换后的后缀数组放到了小波树上,这样使得查询复杂度仅跟小波树的高度有关,而跟文本的尺寸无关,在巨大的文本序列基础上,这是多么大的性能提升!这就是著名的以他们名字首字母命名的FM-Index,是已知小波树最成功的用途之一。
第二个例子是倒排索引。假定目前我们针对某文档集合需要构建索引,同时还需要提供词在每个文档中的位置信息,如果按照倒排索引的做法,我们需要同时存储文本信息和倒排索引本身,而如果把文档表示为一个巨大的字符串插入到小波树之中,我们可以仅仅使用一个压缩数据结构小波树而无需任何其他开销。在该小波树中,为了能够提取任何原始文本,我们只需要采用Lookup操作;为了访问某个词C对应的倒排链的第i个位置,我们只需要调用Select(i,C)操作,进一步的,Rank操作可以继续扩展为针对序列多个区间之间求交,所以我们甚至可以直接把构建好的倒排索引插入到小波树中,这甚至能够提供比原始倒排表还快的检索性能——因为小波树的求交复杂度跟文档数量无关!
第三个例子是图。一个图常见的表示形式是邻接列表。给定这样一种数据结构,我们可以列出任何一个图节点的相邻节点。如果我们把这样的邻接列表放到小波树中会如何呢?我们可以以常数时间获取到任何一个图节点的某一个相邻节点,以常数时间获取到某几个图节点共同的相邻节点——看到这里聪明的读者想到了什么?微博的共同关注,以常数时间获取!
当然,小波树并不是没有缺点的,首先,它只能够存在于内存之中,迄今我们还没有发现一个可以在硬盘或者SSD上表征小波树的手段;其次,它是一个静态数据结构,这意味着只要有数据发生变化,我们不得不重新构建整个小波树而无法做到增量更新。然而,这并不妨碍它成为一款来自学术界的出色工具,有了它的协助,我们将得以在某些场景下提供极速的访问性能。目前,小波树在国内基本上属于无人知晓包括BAT,然而所有它的使用者都获得了丰厚的回报——在系统设计上,永远是算法 > 架构,因为前者往往带来的是数量级的性能提升。最后顺道提及一下,在看到“算法”二字时,大多数人的反应是诸如<算法导论>,程序设计竞赛等等,固然这些很重要,也很烧脑,然而对于现代大型系统构建,这些通用的算法早已经不是在工作中能够用到的范畴,我们所提的算法,更多是指能够在系统层面上带来质变的创新,获取它们的渠道几乎只有源源不断的学术界创新。
树堆(Treap)
Treap的定义
树堆(Treap)是二叉排序树(Binary Sort Tree)与堆(Heap)结合产生的一种拥有堆性质的二叉排序树。
但是这里要注意两点,第一点是Treap和二叉堆有一点不同,就是二叉堆必须是完全二叉树,而Treap并不一定是;第二点是Treap并不严格满足平衡二叉排序树(AVL树)的要求,即树堆中每个节点的左右子树高度之差的绝对值可能会超过1,只是近似满足平衡二叉排序树的性质。
Treap每个节点记录两个数据,一个是键值,一个是随机附加的优先级,Treap在以关键码构成二叉排序树的同时,又以结点优先级形成最大堆和最小堆。所以Treap必须满足这两个性质,一是二叉排序树的性质,二是堆的性质。如下图,即为一个树堆。
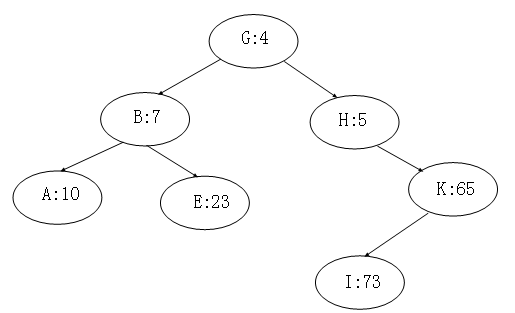
Treap的特点
Treap因在BST中加入了堆的性质,在以随机顺序将节点插入二叉排序 树时,根据随机附加的优先级以旋转的方式维持堆的性质,其特点是能基本实现随机平衡的结构。相对于其他的平衡二叉搜索树,优点是实现简单,因为Treap维护堆性质的方法只用到了旋转,只需要两种旋转,易于维护,可用于高效快速查找。
Treap的操作
插入
给节点随机分配一个优先级,先和二叉排序树(又叫二叉搜索树)的插入一样,先把要插入的点插入到一个叶子上,然后再维护堆的性质。
以最小堆为例,如果当前节点的优先级比其根节点小就旋转。如果当前节点是根的左子节点就右旋。如果当前节点是根的右子节点就左旋。 即左旋能使根节点转移到左边,右旋能使根节点转移到右边。
下图中,当X节点优先级小于Y节点时右旋和Y节点优先级小于X节点的左旋,其左右旋转如下图:
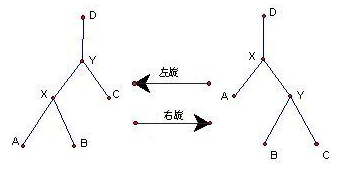
插入写成递归形式的话,只需要在递归调用完成后判断是否满足堆性质,如果不满足就旋转,实现相对简单。其插入过程示例图如下:
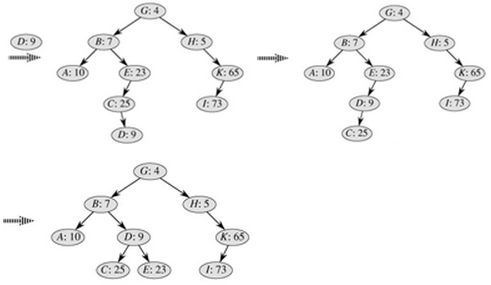
时间复杂度: 由于旋转是O(1)的,最多进行h次(h是树的高度),插入的复杂度是O(h)的,在期望情况下h=O(log n),所以它的期望复杂度是O(log n)。
删除
(1)找到相应的结点; (2)若该结点为叶子结点,则直接删除; (3)若该结点为只包含一个叶子结点的结点,则将其叶子结点赋值给它; (4)若该结点为其他情况下的节点,则进行相应的旋转,具体的方法就是每次找到优先级最小的儿子,向与其相反的方向旋转,直到该结点为上述情况之一,然后进行删除。
时间复杂度: 最多进行O(h)次旋转,期望复杂度是O(log n)。
查找
根据Treap具有二叉搜索树的性质,可以快速查找所需节点。 时间复杂度: 期望复杂度是O(log n)。
二叉堆(binHeap)
堆的定义
堆(heap),这里所说的堆是数据结构中的堆,而不是内存模型中的堆。堆通常是一个可以被看做一棵树,它满足下列性质:
[ 性质一 ] 堆中任意节点的值总是不大于(不小于)其子节点的值;
[ 性质二 ] 堆总是一棵完全树。
将任意节点不大于其子节点的堆叫做最小堆或小根堆 ,而将任意节点不小于其子节点的堆叫做最大堆或大根堆 。常见的堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等等。
二叉堆的定义
二叉堆是完全二元树或者是近似完全二元树,它分为两种: 最大堆和最小堆 。
最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。示意图如下:
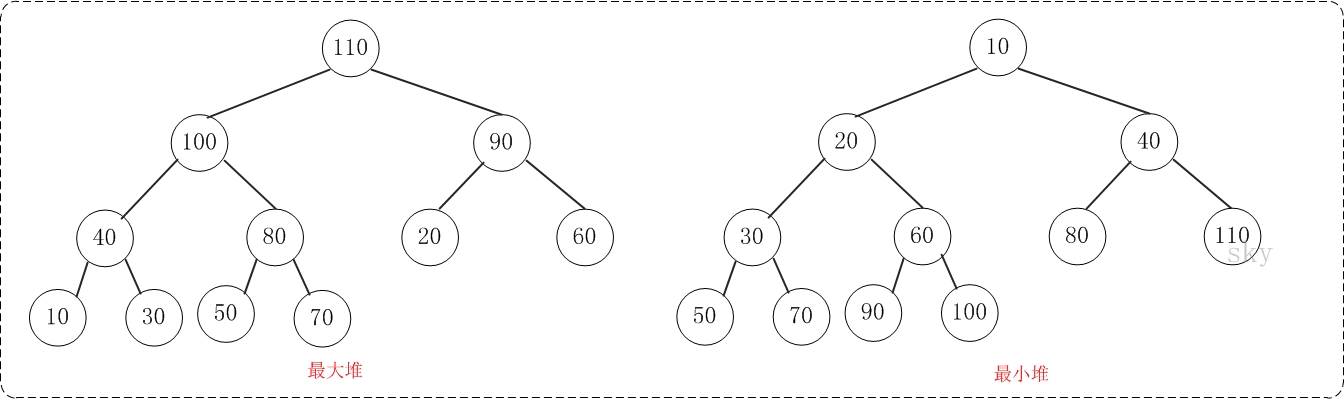
二叉堆一般都通过" 数组 "来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。有时候,我们将"二叉堆的第一个元素"放在数组索引0的位置,有时候放在1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。 假设"第一个元素"在数组中的索引为0的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2i+1);
(02) 索引为i的左孩子的索引是 (2i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);
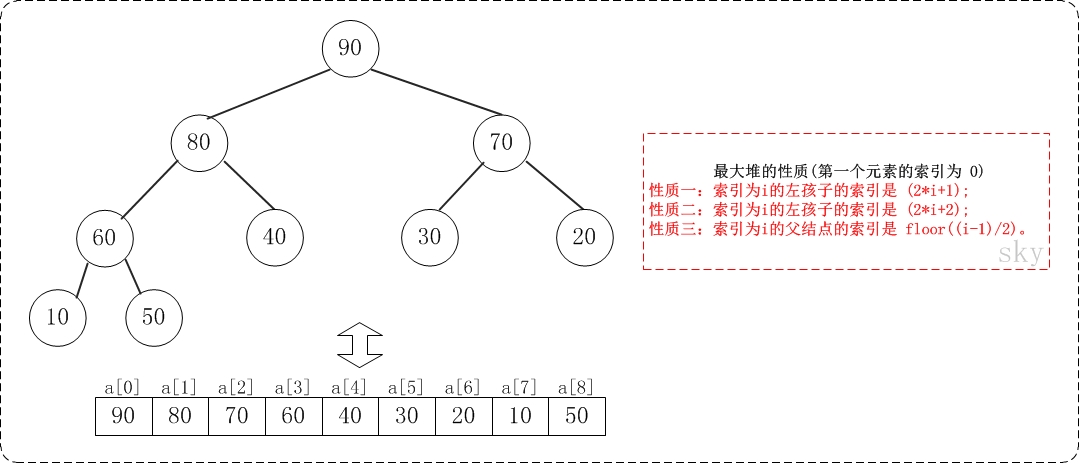
假设"第一个元素"在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2i);
(02) 索引为i的左孩子的索引是 (2i+1);
(03) 索引为i的父结点的索引是 floor(i/2);
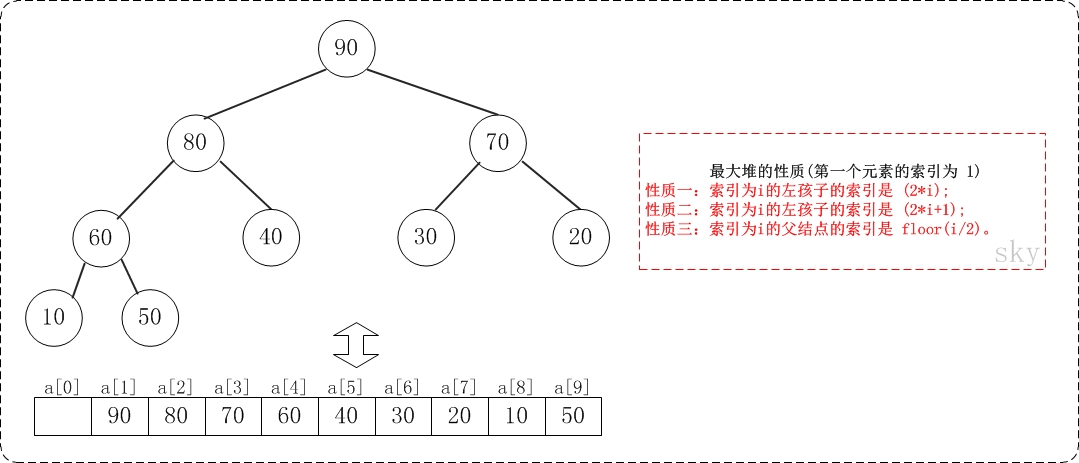
注意:本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式!
在前面,我们已经了解到:"最大堆"和"最小堆"是对称关系。这也意味着,了解其中之一即可。本节的图文解析是以"最大堆"来进行介绍的。
二叉堆的核心是"添加节点"和"删除节点",理解这两个算法,二叉堆也就基本掌握了。下面对它们进行介绍。
1. 添加
假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85,需要执行的步骤如下:
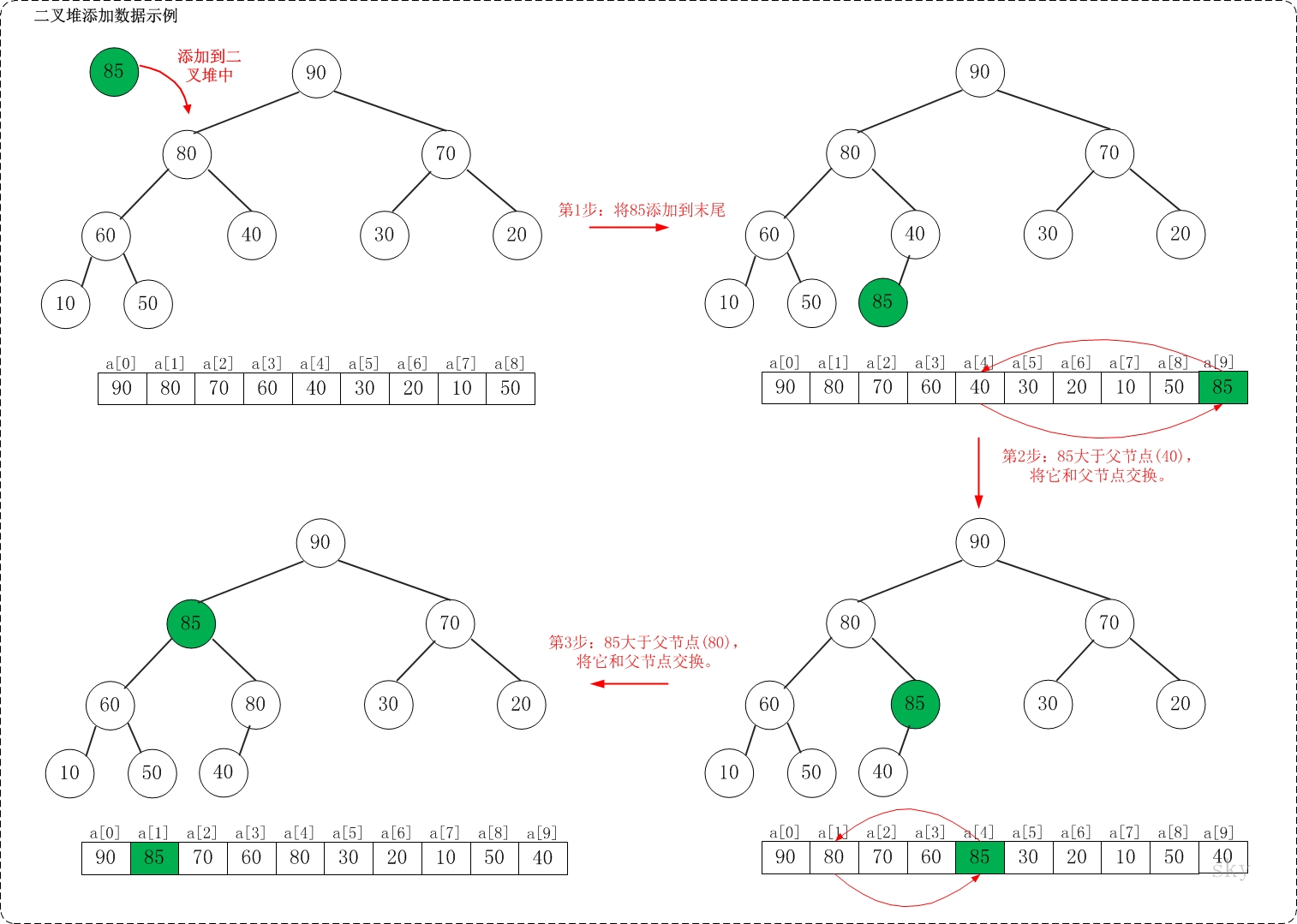
如上图所示,当向最大堆中添加数据时:先将数据加入到最大堆的最后,然后尽可能把这个元素往上挪,直到挪不动为止!
将85添加到[90,80,70,60,40,30,20,10,50]中后,最大堆变成了[90,85,70,60,80,30,20,10,50,40]。
跳表(skipList)
跳表是一种可以替代平衡树的数据结构。跳表追求的是概率性平衡,而不是严格平衡。因此,跟平衡二叉树相比,跳表的插入和删除操作要简单得多,执行也更快。
二叉树可以用来实现字典和有序表等抽象数据结构。在元素随机插入的场景,二叉树可以很好应对。然而,在有序插入的情况下,二叉树就退化了(链表),性能非常差。如果有办法对待插入元素进行随机排列,二叉树大概率可以运行良好。大部分情况下,插入是在线进行的,因此随机排列并不具有可行性。平衡树在操作时对树结构进行调整以满足平衡条件,因此获得理想性能。
跳表是一种概率性可行的平衡二叉树替代数据结构。跳表通过一个随机数生成器实现平衡。虽然跳表最坏情况下(worst-case)性能也很差,但是没有任何输入序列必然会导致最坏情况发生(这点类似划分元素(pivot point)随机选定的快排)。跳表极度不平衡发生的概率非常低(一个包含250个元素的字典,一次查找需要花3倍期望时间的概率小于百万分之一)。跳表平衡概率跟随机插入的二叉树差不多,好处是插入顺序不要求随机。
实现概率性平衡比严格控制平衡要简单得多。对很多应用来说,跳表用起来比平衡树更自然,而且算法更简单。跳表算法简单性意味着更容易实现,而且与平衡树和自适应树相比有常数倍数的性能提升。跳表在空间上也比较高效。平均每个元素只需要额外耗费个2指针(甚至可以配置得更低),并不需要在每个节点上都存与平衡和优先级相关的数据。
结构
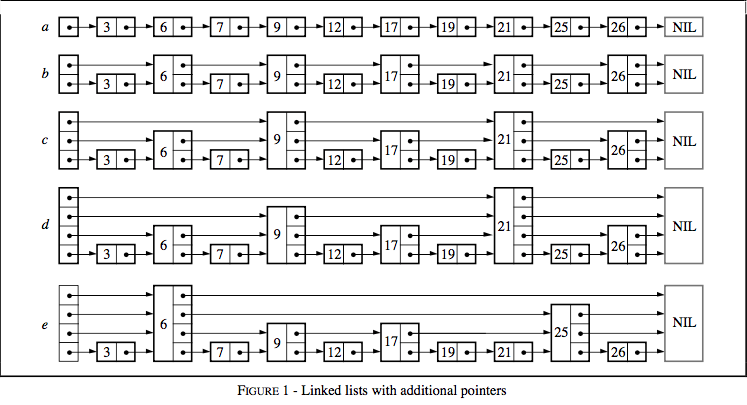
搜索一个链表时,我们需要遍历每个节点(如图 1a)。如果列表是有序的,偶数节点另存一个指向下一个偶数节点的指针(如图 1b),我们只需要检查最多(n/2)+1个节点(n是链表规模)。如果序号为4的倍数的节点都有一个往前跳4步的节点,那么最多只需要检查(n/4)+2次。如果,序号为2^i的节点有一个向前跳2^i步的指针,那么则需要检查log2 n次了!这种数据结构可以用来做快速搜索,但是插入和删除并没有可行性。
有k个前进指针的节点成为k层节点。如果第2^i个节点有一个向前跳2^i步的指针,那么每层节点数满足以下关系:第1层有50%的节点;第2层有25%的节点;第3层有12.5%的节点;以此类推。假设每层的比例还是一样,但是节点随机选择,会怎样呢(图 1e)?节点第i个前进指针不严格跳2^i步,而是可以跳任意步。由于不需要维持特殊条件,插入节点层数随机生成,插入和删除只需要做局部修改。极端情况下,有些层次分布会导致极差的性能,不过接下来我们会看到这种情况非常罕见。这种数据结构在链表的基础上加上额外指针以跳过一些中间节点,因此命名为跳表。
算法
这小节介绍用于搜索、插入、删除的算法。搜索操作返回与给定键(key)关联的值(value),键不存在时则失败。插入操作将给定键关联到新的值,如果键不存在则插入新的节点。删除操作删除给定键。另外,类似最小键和下一键这类操作实现起来也非常简单。
每个元素由一个节点表示,层次由节点在插入时随机选定,与已有元素无关。层次为i的节点拥有i个前进指针,下标分别是1至i。节点不需要存储层数。选定一个合适的常量MaxLevel,层数在这个范围内。跳表的层数时当前所有节点层数的最大值,或者当跳表为空是,层数为1。用一个头向量存储从层次1到MaxLevel的向前指针。指针高于当前跳表层数的部分直接指向NIL。
初始化
约定NIL元素,其键比所有合法建都大(上限)。跳表的任意层都以NIL结尾。新的跳表初始化成层数只有1,并且所有表头所有前进指针都指向NIL。
查找
查找某个元素时,需要逐层遍历所有键不超过给定键的节点。如果当前层前进节点已经不符合条件了,往下一层开始遍历。当遍历进行到第1层时,下一个节点就是目标节点(如存在)。
插入/删除
插入或者删除节点,只需先执行搜索操作,然后视情况重新拼接。
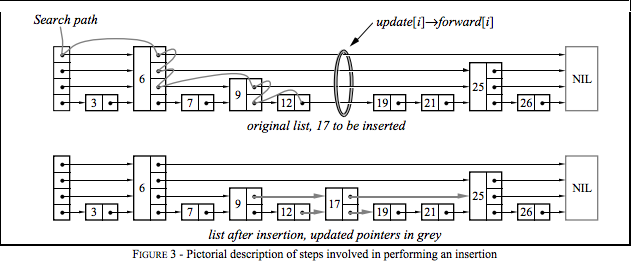
搜索的过程中维护了一个名为update的向量,在每次降层搜索时更新。搜索完成后,update刚好记录了各层在操作位置(图中环)左边最近的节点:
| 元素 | 节点 |
|---|---|
| update[1] | 12 |
| update[2] | 9 |
| update[3] | 6 |
| update[4] | 6 |
如果插入时生成了一个比当前最大层更大的层数,则需要更新跳表层数并且初始化update向量对应部分。
在每次删除时,需要检查被删除节点是否是最大层节点。如果是,需要对跳表层数做对应调整。
随机函数
确定一个随机数生成函数,其概率分布使得第i层中有50%的节点同时数据第i+1层。先抛开具体数值,我们在讨论一个分数p,对于有i层指针的节点中p部分,同时拥有i+1层指针。以下便是一个非常理想的随机数生成函数,随机层数生成与跳表元素及规模无关。
def random_level(self) -> int:
"""
:return: Random level from [1, self.max_level] interval.
Higher values are less likely.
"""
level = 1
while random() < self.p and level < self.max_level:
level += 1
return level
│ b1_binaryTree.py 二叉树
│ b2_binary_search_tree.py 二叉搜索树
│ b2_binary_search_tree_recursive.py 二叉搜索树递归
│ b2_binary_tree_mirror.py 二叉搜索树镜像
│ b2_binary_tree_traversals.py 二叉搜索树遍历
│ b3_avl_tree.py AVL树
│ b3_balance.py AVL树
│ b4_red_black_tree.py 红黑树
│ b5_lazy_segment_tree.py 线段树Lazy-Tag
│ b5_segment_tree.py 线段树add
│ b5_segment_tree_other.py 线段树 add/max/min
│ b6_fenwick_tree.py 二分索引树
│ b7_treap.py 树堆
│ b8_trie.py 字典树
│ b9_wavelet_tree.py 小波树
│ b10_binheap.py 二叉堆
│ b10_bst.py 二叉搜索树
│ b11_skip_list.py 跳表
│ __init__.py
│ 树Tree.md 学习笔记
公众号:数据极客 《一种神奇的数据结构—小波树》 ↩︎



